基于地球坐標系的SINS/GNSS極區組合導航算法
張甲甲,卞鴻巍,王榮穎,馬 恒
(海軍工程大學電氣工程學院,武漢 430033)
0 引言
極區冰層的快速減少,使北極航道逐漸成為新的海上交通動脈。隨著對極區導航問題的日益重視,人們針對傳統的力學編排方案在極區不再具備導航能力的問題,提出了諸多適用于極區導航的慣導力學編排方案,如極區平面導航、極區格網導航、橫向坐標系導航[1]等。然而無論哪種形式的慣導編排,都會表現出慣導固有的特性,如穩定性、振蕩性以及對初始條件做出的響應[2],這些特性對慣導系統精度將產生嚴重影響。
為保證艦船在極區可以長航時高精度工作,國內外學者對極區阻尼及組合導航技術進行了相關研究[3-8]。文獻[3]提出了適用于極區的橫坐標系捷聯慣導系統(Strapdown Inertial Navigation Sy-stem,SINS)阻尼技術;文獻[4]參考傳統指北方位慣導力學編排方案,提出了一種基于橫坐標系的SINS/多普勒計程儀(Doppler Velocity Log,DVL)組合方案;文獻[5]在格網坐標系框架下推導了格網慣性力學編排方程和導航誤差方程,結合星跟蹤器的輸出提出了慣性/星跟蹤器極區組合方案;文獻[6]提出了極區游動坐標系下的慣性導航系統(Inertial Navigation System,INS)/全球定位系統(Gl-obal Positioning System,GPS)組合導航方案。但是,文獻[3-5]的慣導編排都是基于地球球體模型的,存在原理性誤差;文獻[6]提出的組合導航方案不具有穿越極點的能力。
綜上所述,本文結合全球衛星導航系統(Global Navigation Satellite System,GNSS)全球性和高精度等優點[9-10],研究了一種基于地球坐標系的SINS/GNSS極區組合導航算法,在地球橢球模型的框架下定義了橫向坐標系,將地球坐標系確定為慣導計算坐標系,卡爾曼濾波器估計的姿態、速度和位置誤差是相對于地球坐標系的,再將地球坐標系下的導航結果轉換到橫向坐標系。相對于當地水平坐標系算法,地球坐標系下的捷聯算法和卡爾曼濾波算法在保證導航精度的情況下,計算效率可以分別提升40%和10%[11],對實現高精度的導航及濾波算法十分有利。結果表明,地球坐標系下的組合導航算法滿足極區航行的需求。
1 基于地球橢球模型的橫向坐標系設計
如圖1所示,定義0°經線和180°經線組成的大橢圓為橫向赤道,取90°E經線和90°W經線的北半球部分組成的半個大橢圓為0°橫向經線,定義原地理坐標點(0°,90°E)和(0°,90°W)分別為橫向北極點和橫向南極點。橫向地球坐標系與地球固聯,取地球橢球體模型的中心作為坐標原點,X′ 軸指向傳統北極N,Y′ 軸指向格林尼治子午線與赤道的交點,Z′ 軸指向橫北極點。
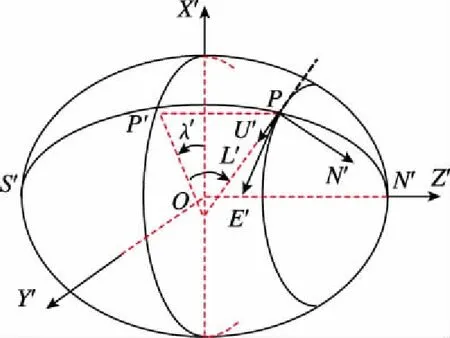
圖1 橢球橫向坐標系Fig.1 The transversal coordinate frame based on the earth ellipsoid model
地球表面上任意一點P的橫向緯度定義為地球橢球面外法線與橫向赤道面的夾角,其橫向經度為地球橢球面外法線在橫向赤道面上的投影與OX′ 軸的夾角。定義橫向地理坐標系(n′)的橫地向軸D′沿參考橢球體的法線方向,橫北向軸N′在垂直于D′軸的平面內,指向橫北極的方向,根據右手定則確定橫東向軸E′。
根據以上定義,利用幾何關系可以得到橫向經緯度與地球坐標的關系為
(1)
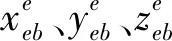
依據傳統經緯度與地球坐標的關系為
(2)
可得,傳統經緯度與橢球橫向經緯度的變換公式為
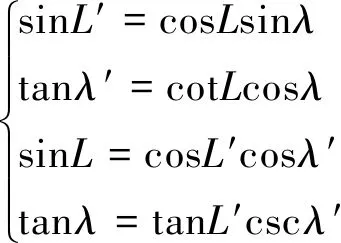
(3)
根據式(3),RN用橫向經緯度表示為
(4)
式中,R0為赤道半徑。
慣導系統直接輸出地球坐標系下的導航參數,經過以下變換可得到橫向地理坐標系下的導航參數。根據定義可以得橫向地球坐標系與橫向地理坐標系的坐標轉換矩陣為
(5)
從地球坐標系到橫向地球坐標系的坐標轉換矩陣為
(6)
由式(6)可以得到,地球坐標系到橫向地理坐標系的坐標轉換矩陣為
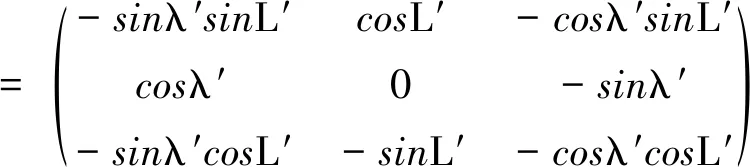
(7)
則橫向地理坐標系下的速度為
(8)
橫向地理坐標系下的姿態矩陣為
(9)
由式(1)可得,由地球坐標系下的位置到橫向地理坐標系下的位置的計算式為
(10)
由于式(10)中等式右側包含L′、λ′、RN項,且RN是橫向經緯度的函數,故式(10)需經過多次迭代才能得到。一般可取前一時刻的橫向位置作為迭代初值。
2 地球坐標系下的慣導編排
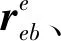
(11)
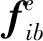
(12)
(13)
其中,μ為地球引力常數,取值為3.986004418×1014m/s2,J2為地球第二引力常數,取值為1.082627×10-3[13]。
慣性導航系統誤差模型不僅是系統誤差分析與控制的基礎,而且還可用于系統中實時故障檢測和卡爾曼濾波的執行。捷聯慣導系統在地球坐標系下的誤差模型可表示為[14]
(14)
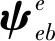
(15)
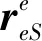
3 地球坐標系組合導航算法
在本文研究的SINS/GNSS組合導航系統(見圖2)中,捷聯慣導系統選用地球坐標系作為導航解算坐標系,衛星導航系統直接輸出地球坐標系下的位置和速度信息作為量測量輸入到卡爾曼濾波器,對SINS誤差進行估計。將濾波器估計的SINS誤差反饋到慣導系統中對導航參數進行校正,再對校正后的地球坐標系下的導航參數進行導航信息轉換,得到橫向地理坐標系下的導航參數構成組合導航系統輸出。
3.1 系統狀態方程
(16)
根據式(14)可得系統狀態方程為
(17)
式中,ws為系統噪聲向量,G為系統噪聲分布矩陣,系統矩陣F表示為
(18)
其中
(19)
3.2 系統量測方程
將GNSS測量的地球坐標系下的載體位置、速度與慣導輸出的位置、速度的差值作為觀測量,建立量測方程為
(20)
則量測方程的矩陣形式為
z=Hx+wm
(21)
式中,wm為量測噪聲,用I3表示三階單位陣,測量矩陣近似為
(22)
4 仿真驗證
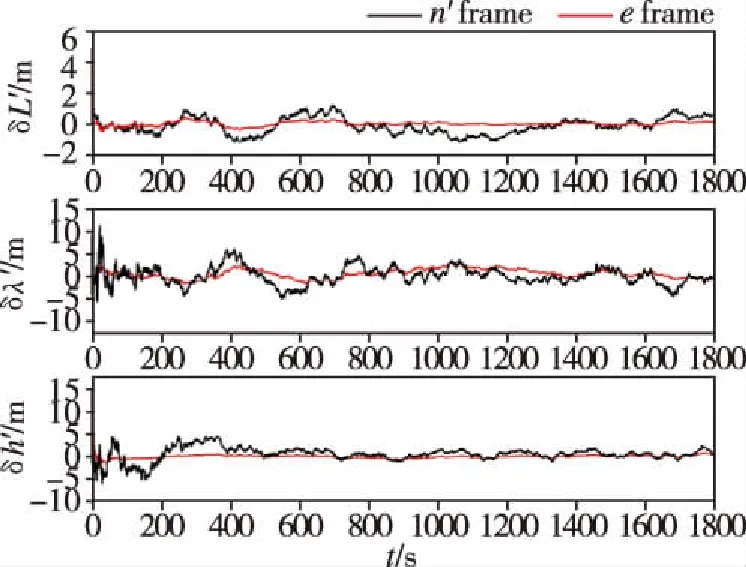
圖3 橫向位置誤差對比Fig.3 Comparison of transverse position errors
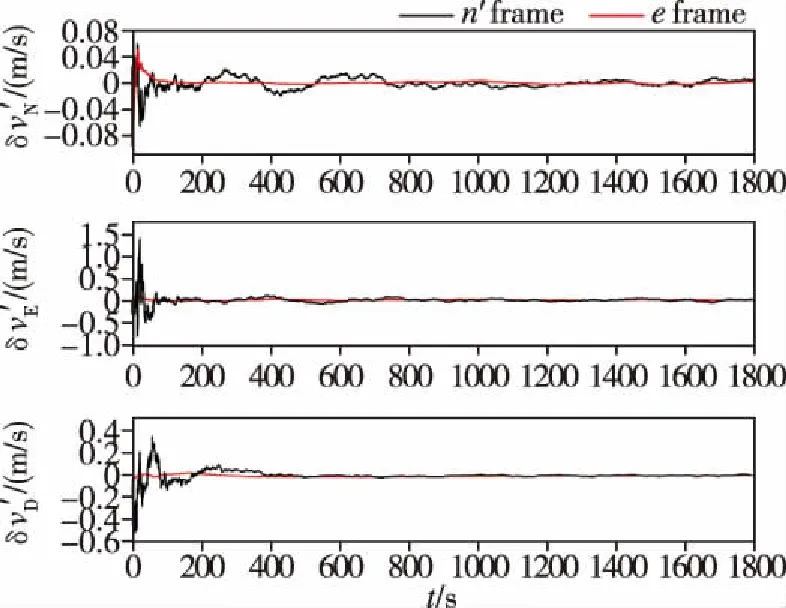
圖4 橫速度向誤差Fig.4 Comparison of transverse velocity errors
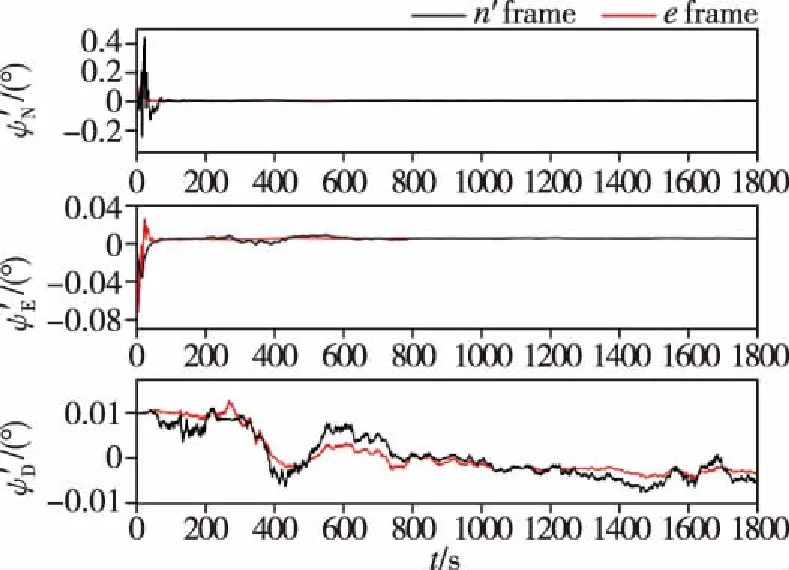
圖5 橫向姿態誤差對比Fig.5 Comparison of transverse attitude errors
由圖3~圖5可得,在1800s的仿真時長內,兩種組合導航方法輸出的橫向地理坐標系下的導航信息均獲得了較好的收斂效果。基于地球坐標系的SINS/GNSS極區組合導航方法的橫向定位誤差不超過2m,橫向速度誤差不超過0.02m/s,姿態精度達到0.4′。在1100s左右穿過極點時,各導航信息未發生跳變,系統十分穩定。其中地球坐標系下的組合導航方法得到的位置和航向精度優于橫向地理坐標系下的組合導航方法,且輸出導航信息更加穩定。這是因為在極區范圍內,地球表面形變較大,不能很好地與地球橢球模型吻合,而地球坐標系下的組合導航方法脫離了地球橢球模型假設,具有更高的導航精度。由此可以看出,本文研究的組合導航系統能有效解決極區環境下慣性導航系統誤差隨時間積累的問題,滿足極區航行作業的需求。
5 結論
本文研究了一種基于地球坐標系的極區SINS/GNSS組合導航算法,給出了橫向坐標系的定義,建立了地球坐標系與橫向坐標系之間的轉換關系。捷聯慣導系統的計算更新在地球坐標系下完成,將GNSS測量的地球坐標系下的載體位置、速度與慣導輸出的位置、速度的差值作為觀測量進行濾波估計,最后將解算結果轉換到橫向坐標系下。算法在保證導航精度的情況下,大幅度提升了計算效率。仿真結果表明,該算法滿足極區航行的要求,并且在艦船穿越極點時,也可提供高精度的導航信息。

