基于可靠性分析的立方星網絡維護架構優化
符弘嵐,張皓,高揚
1. 中國科學院 空間應用工程與技術中心,北京 100094 2. 中國科學院大學 計算機與控制學院,北京 100049
立方星是一種以1U (10 cm×10 cm×10 cm)為基本單元的可擴展小型衛星,與傳統衛星相比其開發周期短且研制成本低[1-3]。立方星體積小重量輕,配備的傳感器、執行機構等硬件精度差,需要設計專門的控制算法抵消低精度帶來的定姿、控制誤差[4],這導致立方星在功能上比不上大型衛星,因此在開發應用初期立方星主要用于技術驗證和作為教育平臺使用[5]。為了更好地發揮立方星的優勢,人們使用大量立方星以較低成本形成分布式空間傳感器網絡,實現傳統單個衛星無法實現的功能[5]。構建立方星星座以執行商業、科學、技術驗證任務已經率先在近地軌道實現。例如,Planet Labs建立了由120多顆Dove衛星組成的星座[6]。噴氣推進實驗室(JPL)設計在低地球軌道(LEO)上部署雨立方星座(Raincube Constellation)形成空間雷達網絡[7]。除了執行近地空間任務,立方星星座在輔助深空探測任務領域也具有巨大潛能。如Chen 等提出在地月L2點部署4顆立方星為月球背面的用戶提供定位服務[8]。
立方星通常作為搭載載荷與其他主要載荷一同發射。到達預定軌道后,由部署系統利用彈簧機構彈射出去[9-10],發射和彈射過程的振動會影響立方星的功能而降低任務成功率,統計數據顯示立方星失敗任務中約20%發生在發射和部署階段[11]。另外可以用軟袋將立方星打包發射到天基平臺,如國際空間站(ISS)上[12],等待部署命令。ISS作為立方星部署的中轉站,可以降低立方星在發射過程中遭受的振動級別,提高任務成功率。
分布式立方星網絡立方星數目多,相較于傳統衛星星座呈現出新的特點,立方星的發射成功率、部署成功率、故障發生頻率等不確定性都與傳統衛星不同。截至2018年5月31日,總的立方星任務失敗率仍有25%,且立方星在早期運行階段易發生故障的狀況仍未得到明顯改善[11]。傳統的衛星星座(如導航衛星星座、通信衛星星座、遙感衛星星座)一般會有備份星,在部分衛星失效后啟動,代替故障衛星工作[13-16]。對于分布式立方星網絡,相較于直接從地面發射新的立方星,在軌道上儲存備用立方星可以提高系統對故障的響應性[14]。傳統備份星一般直接被部署于空間軌道,但是立方星更易受到惡劣空間環境的影響,直接暴露于軌道上會降低其壽命而影響備份效果,因此考慮使用在軌倉庫儲存備份立方星。在軌倉庫與運載火箭、服務航天器、備用立方星組成在軌維護架構。然而由于立方星故障隨機發生,用于維護立方星網絡的備用立方星的需求不確定,在軌倉庫應提前存儲多少備用立方星難以確定。此外備用立方星還應適時從地面補充。因此,一個重要的問題是確定備用立方星的發射頻率和發射數量,從而在保證系統性能的同時,降低維護架構的運行成本。由于故障的隨機性,這個問題具有極大的挑戰性。
Gu等提出基于航空部件壽命分布的部件采購策略以處理部件需求的不確定性,并且假定部件壽命服從正態分布[17]。Du Jonchay和Ho描述了一種由運載火箭、機器人服務設備和軌道倉庫組成的機器人在軌服務基礎設施,這篇文章假定故障發生服從泊松過程[14]。然而航天器故障行為并不一定遵守正態分布或者泊松過程[18],真實的模型應該來自真實的數據。部分學者對小衛星數據進行統計分析,結果表明Weibull分布適合用于建模衛星以及衛星子系統的故障行為[19]。
本工作旨在為維護架構優化提供更實際的解決方案,考慮隨機故障行為,優化備用立方星的補給時刻和補給量,以降低維護架構的運行成本。提出了分布式立方星網絡維護架構成本模型。接著收集了立方星故障數據,設計了最大化擬合優度參數估計方法,比較了不同分布類型對故障數據的擬合效果,最終選擇Weibull分布來建模立方星的壽命分布[19-21]。最后結合成本模型和壽命分布模型采用蒙特卡羅仿真和遺傳算法分析了成本模型參數對最優補給策略的影響。
1 維護架構與成本模型
1.1 維護架構
在合適時刻發射備用立方星替換故障立方星可以對立方星網絡進行維護。分布式立方星網絡維護架構如圖1所示,由4部分組成:運載火箭、在軌立方星倉庫、服務航天器和備用立方星(包括地面備份和在軌備份)。該架構進行維護的過程如下:一定數量的備用立方星適時搭載運載火箭到達在軌倉庫,當立方星網絡中有立方星發生故障時,由停靠于在軌倉庫的服務航天器攜帶備用立方星/或者立方星采用自身的軌道機動系統轉移至故障立方星的軌道,替換掉故障立方星,然后服務航天器返回在軌倉庫,等待下次任務。
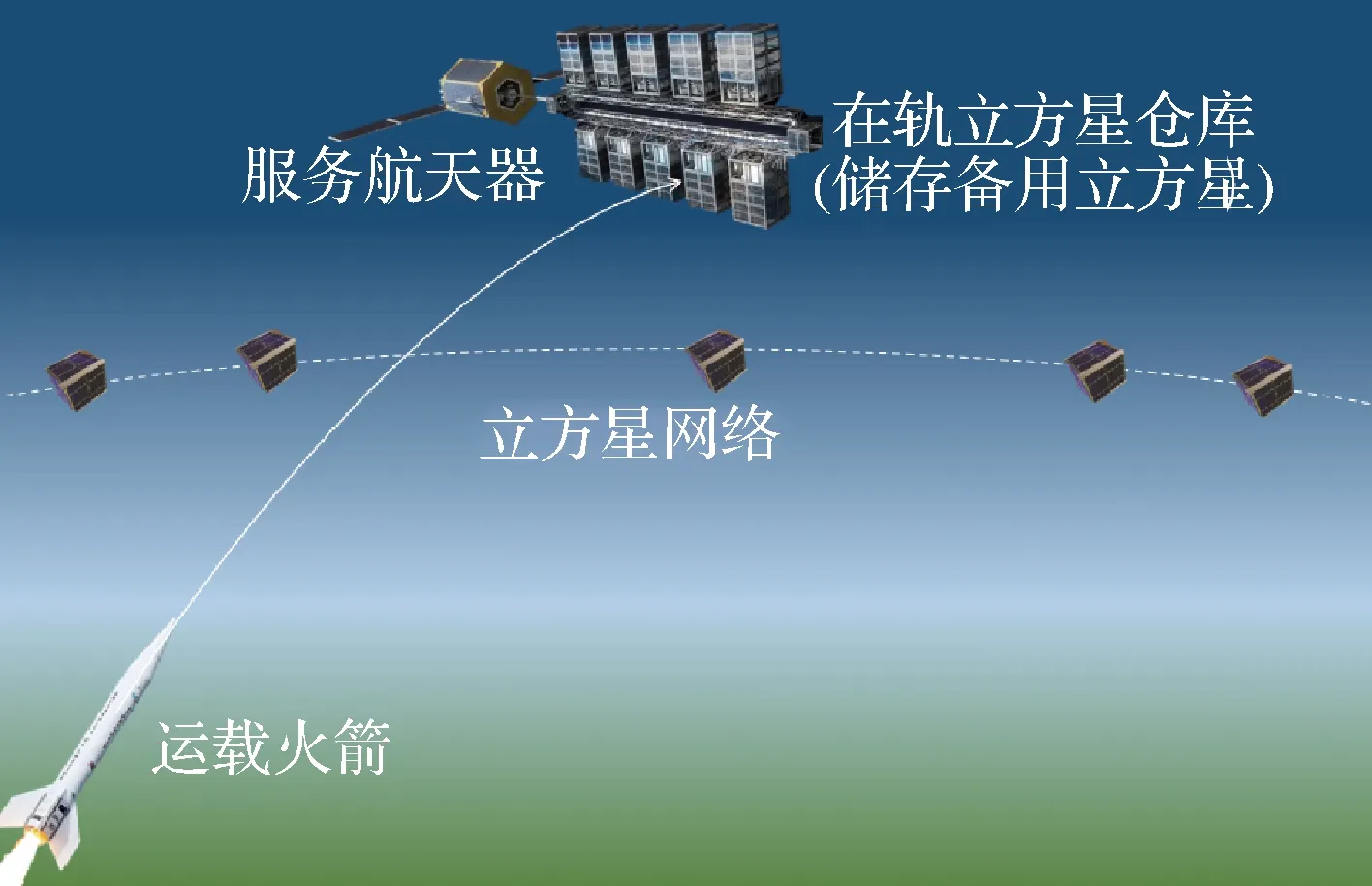
圖1 立方星網絡維護架構Fig.1 Maintenance architecture of CubeSat networks
使用在軌倉庫臨時存儲備用立方星有兩點優勢:① 當網絡損失立方星后,在軌倉庫可以迅速釋放備用立方星,對故障的響應性高;② 在軌倉庫可以提供相對穩定的儲存環境,降低惡劣的空間環境對備用星的影響,提高立方星的壽命。
1.2 成本模型
假定立方星網絡維護架構的運行成本包括3部 分:固定成本、儲存成本和短缺成本[17]。固定成本是指設計和制造立方星的成本;儲存成本是用于為在軌倉庫中的備用立方星提供穩定的儲存環境所產生的成本;短缺成本是指空間傳感器網絡由于未能及時補充立方星而造成的經濟損失。為了簡化分析,本文不考慮地面備份、運載火箭發射成功率和備用立方星軌道轉移成功率、備用立方星從在軌倉庫轉移到目標位置所消耗的時間。
成本模型用到的記號如下:s為單位時間短缺成本;h為單位時間儲存成本;c為立方星的固定成本;T為規劃周期;t為備用立方星到達在軌倉庫時刻;Q為到達在軌倉庫的備用立方星數量;n為故障立方星數量;j為t時刻前故障立方星總數量;tj為第j個故障發生時刻;tk為第k個故障發生時刻。
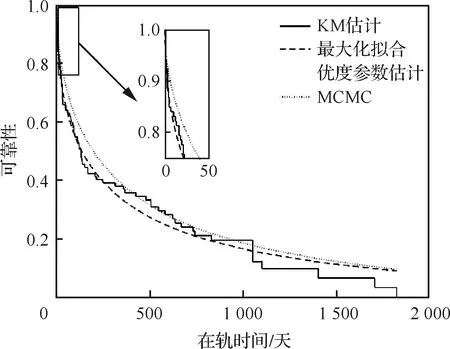
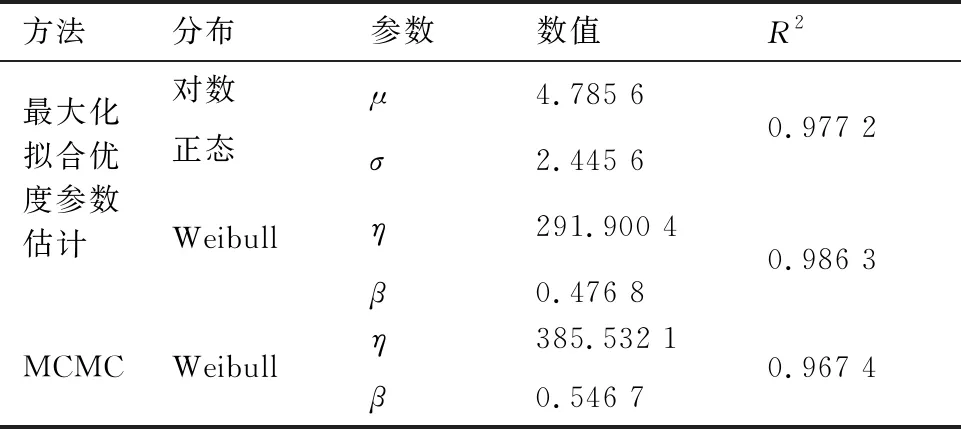
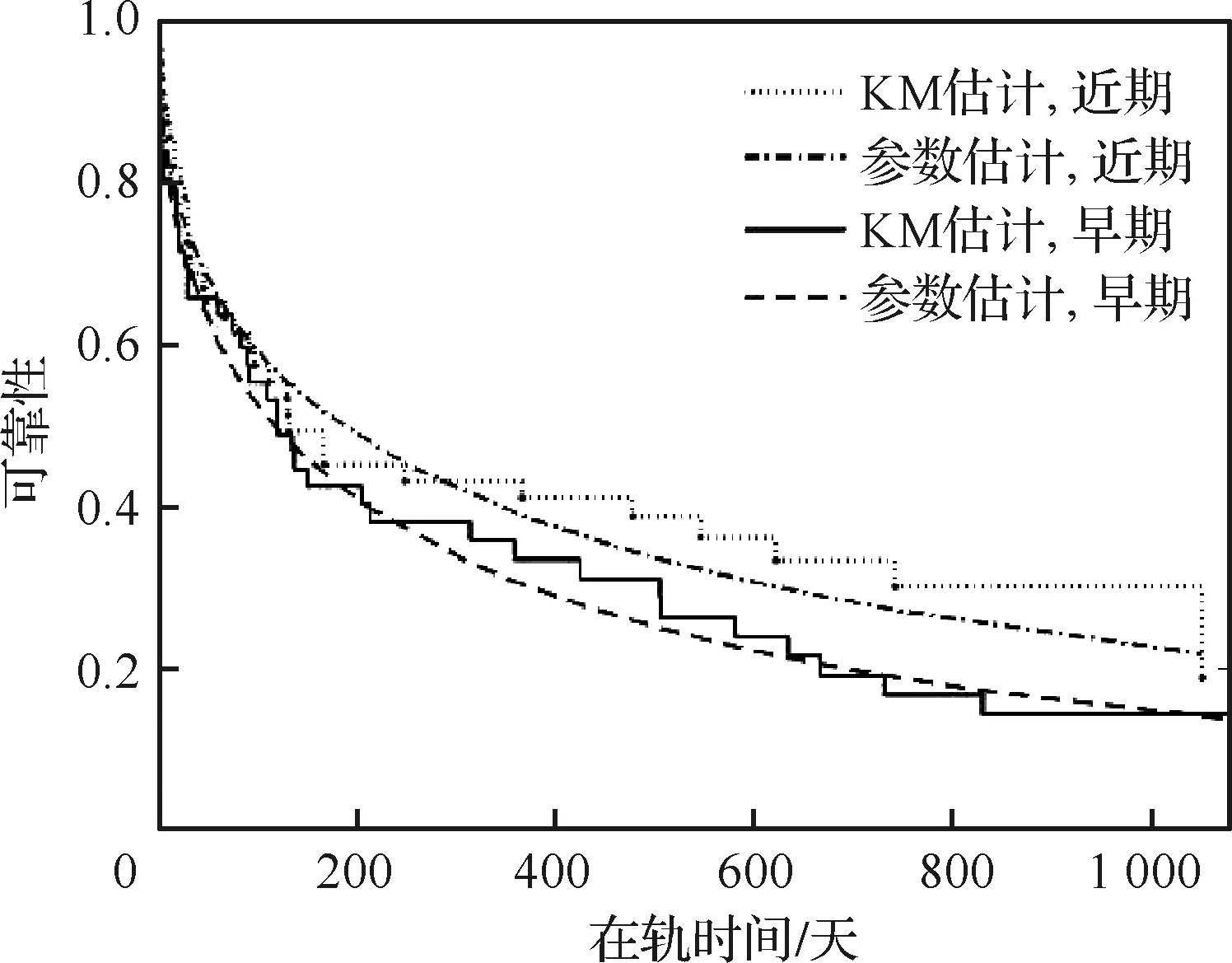
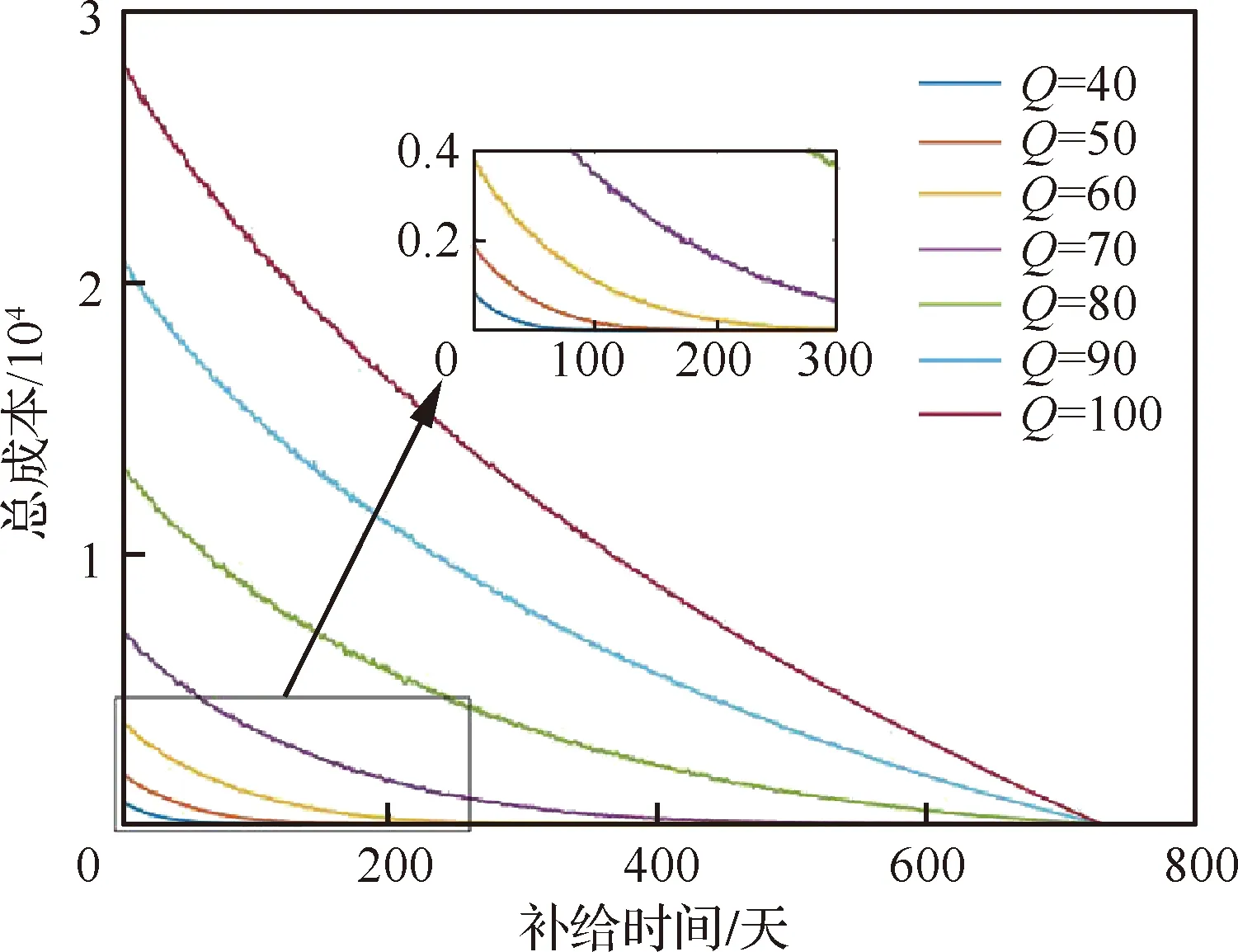
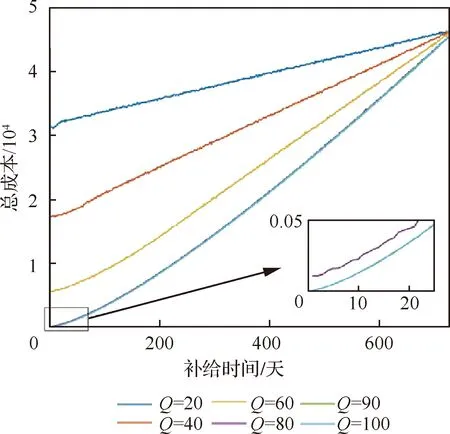
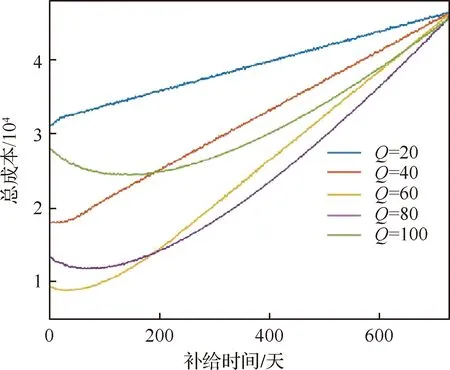
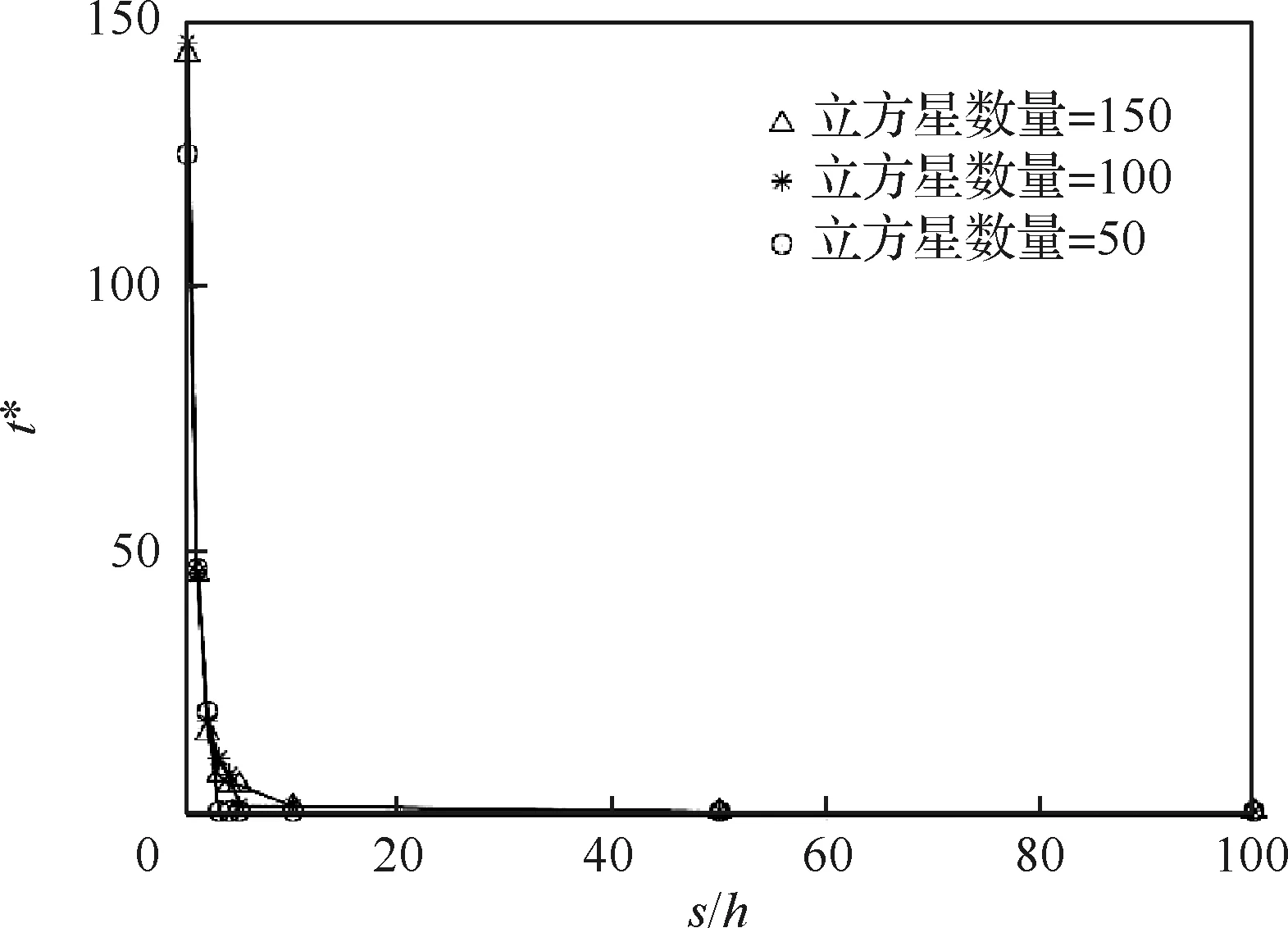
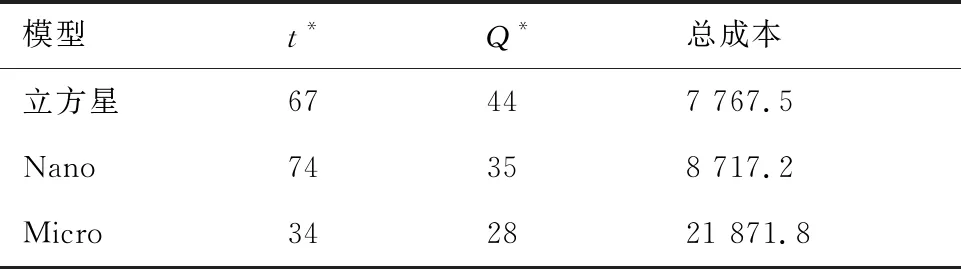
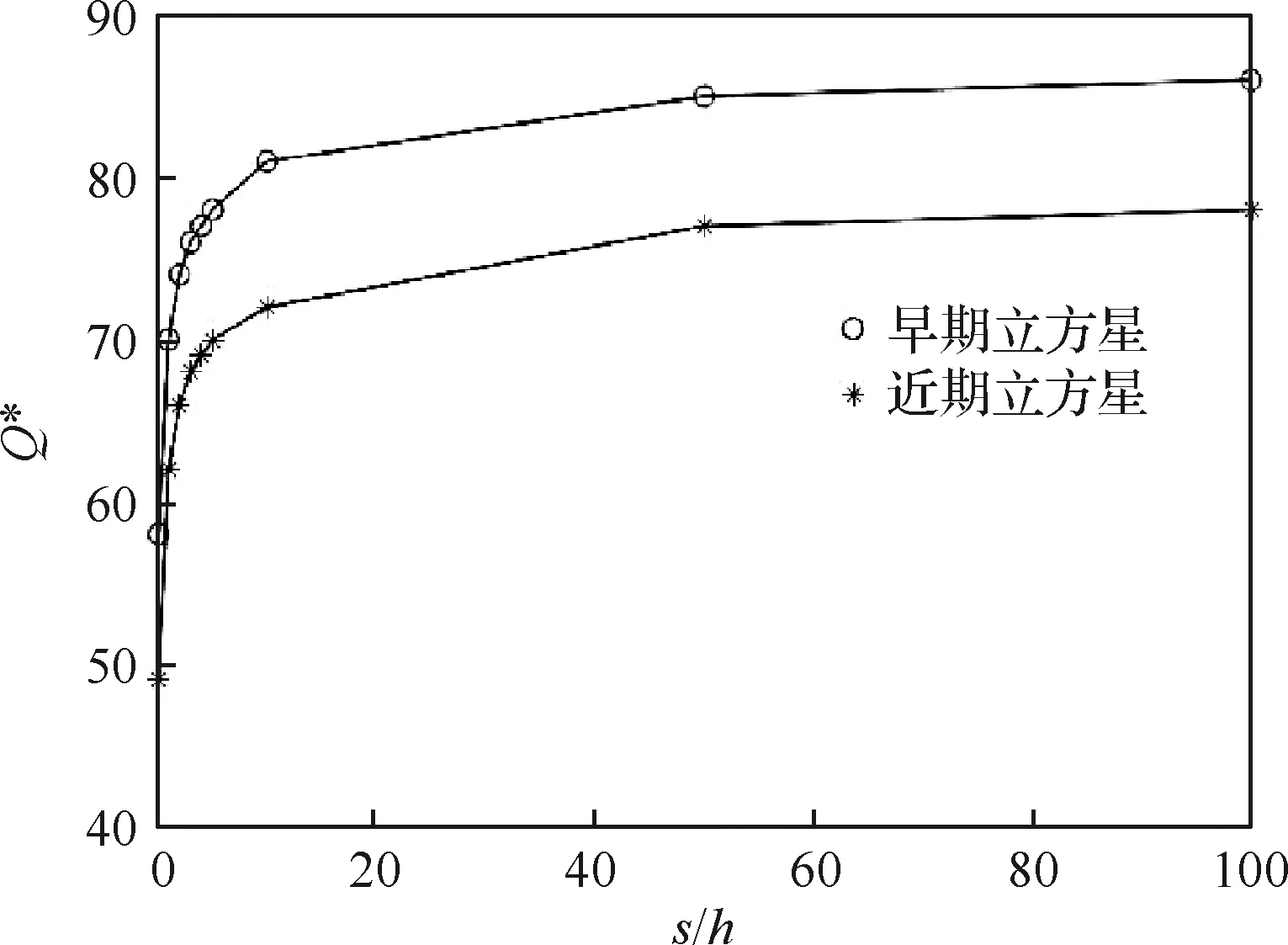
假定新的立方星在t時刻到達在軌倉庫,tj≤t≤tj+1。同時假定在一個規劃周期內共有n顆立方星發生故障。成本模型可以根據Q與j的大小分成5種情況(Q 圖2 成本計算示意圖(j+1 假設Q顆備用立方星在t時刻到達在軌倉庫。其中j顆立即用于替換故障立方星。剩余的Q-j顆備用立方星從t時刻起被儲存在在軌倉庫中。每出現一個新的故障事件就消耗1顆備用立方星,直到第Q個故障發生并消耗掉最后一顆備用立方星,相應的儲存成本為:h(tk-t),k=j+1,j+2, …,Q;短缺成本為:s(t-tk),k=1, 2, …,j。在這之后發生故障的n-Q顆立方星因為缺少備用立方星無法被替換,相應的短缺成本:s(T-tk),k=Q+1,Q+2, …,n。此種情況的總成本計算公式為 (1) 另外4種情況總成本分析方法與第4種情況類似,不再贅述。總的成本模型可統一寫為 M= (2) 可靠性分析方法包括非參數分析方法和參數分析方法。非參數分析不需要假定壽命服從某一分布,適合于不同類型的故障數據,也可以用于評估參數分析的結果。參數分析首先假定壽命服從某一分布,然后估計該分布的參數。 由于立方星網絡維護架構成本分析需要考慮立方星的壽命分布,因此本文選擇參數分析方法,并用非參數分析方法評估參數估計結果。 收集了立方星壽命數據,包括立方星的發射時刻、故障發生時刻或項目結束時刻等[22]。如果立方星一直正常工作到任務完成,即沒有故障發生,這樣的數據稱為右刪失數據。本文獲得的數據包含右刪失數據。 由于一些立方星沒有公開任務運行狀態,最終共收集到111個有效數據,包括84個故障數據,27個刪失數據,數據時間跨度為2000—2018年,足以進行統計分析并用于擬合參數模型。用于可靠性分析的數據示例如表1所示,其中刪失標記0表示故障,1表示刪失。 表1 立方星壽命數據示例Table 1 Lifetime data of CubeSats Kaplan-Meier(KM)估計方法可以從包含刪失數據的故障數據中推導出經驗可靠性函數。可靠性函數又稱為生存函數,對于立方星而言,其可靠性函數表示立方星故障發生在t時刻之后的概率,計算公式為 (3) 式中:ti為故障時刻;ai為ti時刻故障立方星總數量;ni為ti時刻前正常運行的立方星數量,等于立方星總數量減去ti時刻前完成在軌任務的立方星數量(刪失數量)和故障立方星數量。 該可靠性函數是階梯狀函數,在觀察到的故障時刻處不連續,在刪失時刻函數值不變。 參數分析首先需要選擇合適的模型,然后采用參數估計算法估計模型參數。對數正態分布適合用于建模故障率隨時間先增加后降低的對象的壽命分布,Weibull分布可以用于建模故障率隨時間降低、增加、或不變的對象的壽命分布[21]。采用最大化擬合優度估計上述分布的參數。 1) 最大化擬合優度參數估計方法 統計模型的擬合優度表明觀測數據與模型預測值的差異,擬合優度函數值越大表明模型擬合效果越好[19],因此可以對擬合優度函數進行優化,確定模型參數值。 對實際觀測故障數據進行非參數分析得到的可靠性記為R(ti),由參數模型得到的可靠性記為R′(ti,α),α為模型參數,則擬合優度R2計算公式為 (4) (5) (6) (7) 最大化擬合優度參數估計建模為 α*=arg maxR2(α) (8) 采用遺傳算法對式(8)進行求解。 2) 對數正態分布 假定立方星壽命x服從對數正態分布,即lnx~N(μ,σ2),則立方星的可靠性函數為 (9) 式中:erf為誤差函數。 3) Weibull分布 Weibull分布廣泛應用于可靠性分析中,能靈活描述不同故障行為,其PDF和CDF分別為 f(x;β,η)= (10) F(x;β,η)=1-exp(-(x/η)β) (11) 式中:β為形狀參數;η為尺度參數。 假定立方星壽命x服從Weibull分布,則立方星的可靠性函數為 (12) 由1.2節分析可知,分布式立方星網絡維護架構運行成本與立方星的故障時間序列、備用立方星的發射時刻和補給數量有關。因此分析成本模型首先需要生成故障時間序列。以兩年(730天)為一個規劃周期T,假定分布式網絡由Qm顆相同的立方星構成,用Weibull壽命分布模型生成Qm個隨機數,用以代表這Qm顆立方星的壽命,刪除大于730的數,將剩余的隨機數從小到大排序, 即為一個規劃周期內的故障時間序列,記作{t}。 將故障時間序列,備用立方星補給時刻、補給數量代入式(2),可得到維護架構的運行成本。但是由于故障時刻是隨機的,單個故障時間序列對應的總成本隨著補給時刻延后而波動變化,因此采用蒙特卡羅仿真,求N個故障時間序列對應成本的平均值對成本進行分析。 為了求解最小總成本對應的最優補給策略,給出優化模型。采用遺傳算法求解可得到最優補給時刻t*和最優補給數量Q*,即 (13) 式中:{t}l表示第l個故障時間序列。 采用最大化擬合優度方法分別估計了對數正態分布和Weibull分布的參數,同時對比文獻[19] 中結合馬爾可夫鏈-蒙特卡羅(MCMC)仿真的貝葉斯方法,對比了這2種參數估計算法對于立方星故障數據的擬合效果。 非參數分析方法Kaplan-Meier估計得到立方星的可靠性如圖3中的階梯狀曲線所示,可以看出立方星可靠性在初期迅速降低,隨后緩慢降低。 圖3 不同參數估計方法對比Fig.3 Contrast of different parameter estimation methods 參數估計結果列于表2。擬合優度R2越接近于1說明擬合優度越好。對于Weibull分布,最大化擬合優度參數估計方法所得結果的R2比MCMC方法所得結果的R2更大,說明前者的擬合效果更好。如圖3所示,在早期,最大化擬合優度參數估計方法獲得的可靠性函數曲線顯然更靠近KM非參數分析得到的曲線,即該方法能更好地擬合立方星的早期失效率高的特征,也說明了最大化擬合優度參數估計方法擬合精度更高。Weibull分布擬合結果的R2大于對數正態分布擬合結果的R2,說明Weibull分布更適合用于立方星壽命分布的擬合。 表2 參數估計結果Table 2 Parameter estimation results 下面分析最大擬合優度方法Weibull分布擬合結果。β=0.476 8,β<1,表明立方星具有早期失效率高的特點。η=291.900 4,表示立方星的特征壽命為291.900 4天。當t=η時,代入Weibull分布的累計分布函數(CFD),得到F(t)=0.632,表示當立方星網絡運行到第291.900 4天時,可能有63.2%的立方星發生故障。 早期立方星主要用于技術驗證或科學實驗,因此收集的故障數據前一部分以驗證或實驗立方星為主。隨著技術發展,執行商業任務的業務立方星出現[6],對可靠性要求更高。有必要將數據按發射時間等分成早期和近期兩部分,分別進行參數估計,得到兩類可靠性,結果如表3和圖4所示。由表3可知,近期發射的立方星的特征壽命約為415 天,明顯高于早期發射的立方星,但是形狀參數β差別不大,都呈現出早期失效的特點;由圖4 可知近期發射的立方星的可靠性也高于早期的立方星。該對比在一定程度上說明了驗證實驗立方星與業務立方星的差異性,因此在優化業務立方星網絡補給策略時,需要考慮這種差異性。 表3 早期、近期數據參數估計結果 圖4 早期、近期立方星對比Fig.4 Contrast of early and recent CubeSats 分布式立方星網絡維護架構成本模型中有3個 未知參數:c、h、s,通過調節這些參數的大小,可以涵蓋大多數的情形。假定立方星網絡由100顆 立方星組成,分析這3個參數對總成本的影響。 1) 單一成本情況 只考慮固定成本,即c:h:s=1:0:0時,成本模型簡化為:M=cQ,總成本與補給時刻無關,僅與補給數量成正比。 只考慮儲存成本,即c:h:s=0:1:0時,t、Q對總成本的影響如圖5所示,總成本隨著補給時刻延后而降低,隨著補給數量增加而增加。值得注意的是,當補給數量小于60,補給時刻延后至第300天之后時,儲存成本降為零,原因如下:由Weibull分布擬合結果可知立方星的特征壽命約292天,表示當立方星網絡運行到第292天時,可能有63.2%的立方星發生故障;立方星網絡由100顆立方星組成,當運行到292天時,可能有63顆 立方星發生故障,因此在第300天之后補給立方星數量小于60時,這些補給的立方星將全部立即用于替代故障立方星,因此總儲存成本為零。 圖5 儲存成本對總成本的影響(c∶h∶s=0∶1∶0)Fig.5 Effect of holding costs on total costs (c∶h∶s=0∶1∶0) 只考慮短缺成本,即c∶h∶s=0∶0∶1時,t、Q對總成本的影響如圖6所示,總成本隨著補給時刻延后而增加,隨著補給數量增加而降低。當補給數量超過80時,改變補給數量,總成本隨補給時間的變化曲線幾乎重合(如圖6放大圖所示,Q=90與Q=100的曲線幾乎是重合的),這是由于在規劃周期內,總故障立方星數目小于80的概率非常大,補給立方星數目大于80時,所有故障立方星都能被替換,因此總的累積短缺時間是相同的,又由于沒有考慮短缺成本和固定成本,所以總成本相同。 圖6 短缺成本對總成本的影響(c∶h∶s=0∶0∶1)Fig.6 Effect of shortage costs on total costs (c∶h∶s=0∶0∶1) 2) 全部成本情況 同時考慮固定成本、儲存成本、短缺成本,即取c∶h∶s=1∶1∶1時,t、Q對總成本的影響如圖7所示。補給數量較少(大約是Q≤60)與補給數量較多時對總成本的影響存在較大差異:當補給數量較少時,總成本隨著補給數量增加而減少,隨著補給時刻延后而增加;當補給數量較多時,總成本隨著補給數量增加而增加,隨著補給時刻延后先降低后增加。這一差異反應了短缺成本和儲存成本對于總成本不同影響效果,這2種成本分別對應備件短缺和備件冗余2種情況。 圖7 3種成本參數對總成本的影響(c∶h∶s=1∶1∶1)Fig.7 Effect of three cost parameters on total costs (c∶h∶s=1∶1∶1) 由上述分析可得出下述結論:只考慮儲存成本,補給時刻取在立方星的特征壽命292天之后,補給數量小于網絡中立方星總量的63.2%時,總儲存成本為0;只考慮短缺成本,當補給數量Q>80時,總成本不再隨著補給數量增加而變化。當補給數量較少時,短缺成本對總成本的影響占主導;當補給數量較多時,儲存成本對總成本的影響占主導。 分析不同成本比例對于最優補給策略的影響,這里的不同比例指短缺成本與儲存成本的不同比例,由于立方星成本正在逐步降低,因此暫不考慮固定成本,最優補給策略指最優補給時刻t*、最優補給數量Q*;并且對比了立方星網絡不同規模的仿真結果,考慮網絡中立方星數量分別為50、100、150這3種情況。 如圖8所示,隨著s/h比例增大,最優補給時刻均提前,但最優補給時刻與立方星網絡規模無關,都沒有超過150天,均在規劃早期取得,這與立方星的故障行為有關,由4.1節分析可知立方星有早期失效特點,即立方星在軌運行早期發生故障的概率較高,因此在軌運行早期發生故障的立方星數目比在軌運行中期和后期的故障數目要多,所以應該在早期及時補給備用立方星。 圖8 s/h對t*的影響(不考慮固定成本)Fig.8 Influence of s/h on t* (without considering fixed costs) 如圖9所示,考慮不同比例的s/h,立方星網絡最優補給數量大小與規模正相關且變化趨勢相同,隨著短缺成本所占比重增加,最優補給數量也隨之增加,這是由于增大補給數量能夠緩解備件短缺情況。 圖9 s/h對Q*的影響(不考慮固定成本)Fig.9 Influence of s/h on Q* (without considering fixed costs) 將由故障數據和最大化擬合優度方法得到的可靠性模型和文獻[19]中的與立方星質量相接近的Nano衛星、Micro衛星的可靠性模型(如表4所示)分別代入到維護架構補給策略優化模型中,得到3種補給策略,依次記為立方星模型Nano模型、Micro模型;再將3種補給策略和基于數據的可靠性模型代入維護架構,計算總成本。結果如表5所示。 表4 文獻[19]模型參數Table 4 Model parameters of Ref.[19] 表5 不同補給策略比較Table 5 Contrast of different supply strategies Nano模型與立方星模型的結果接近,總成本增加了12.23%;而Micro模型相對于立方星模型結果總成本增加了181.58%。這說明引入適當的實際故障數據對維護架構進行優化的必要性。 由于早期和近期發射的立方星均具有早期失效的特點,都應該在規劃早期補給備用立方星,因此只對補給數量進行對比分析。用早期和近期的立方星可靠性模型,分別求解由100顆立方星組成的網絡的最優補給數量。如圖10所示,對于不同成本比例,近期立方星的補給數量均小于早期立方星的補給數量。由4.1節分析可知,近期發射的立方星的可靠性更高,因此在規劃周期內立方星網絡中發生故障的立方星數量相對更少,所以需要的補給量也少。這一結論說明在優化立方星網絡的維護策略時,應該考慮技術發展導致的可靠性模型的變化。 圖10 早期、近期立方星Q*對比Fig.10 Q* comparison between early and recent CubeSats 1) 立方星壽命分布的參數模型可采用Weibull分布或對數正態分布,進而采用最大化擬合優度參數估計方法進行參數估計,擬合數據表明Weibull模型精度比對數正態分布模型稍高。 2) 立方星具有早期失效率高的特點,由于這一特點,備用立方星最優補給時刻建議為規劃周期早期。目前立方星總的特征壽命大約為292天,近期發射的立方星的可靠性高于早期發射的立方星。 3) 基于本文收集的立方星壽命數據,若在軌服務成本以短缺成本為主,那么建議備用立方星補給時間不晚于第150天,補給數量與立方星網絡規模有關。若以儲存成本為主,建議備用立方星補給數量約等于立方星網絡中立方星總數量的60%,補給時刻不晚于第300天。補給時刻隨短缺成本/儲存成本增加而提前,與立方星網絡規模無明顯相關關系;補給數量隨短缺成本/儲存成本增加而增加。 4) 近期發射立方星的最優補給數量比早期立方星的少,對立方星網絡的補給策略進行優化時,不僅需要選擇合適的可靠性模型,還需要考慮由于技術發展而導致的立方星可靠性模型的變化。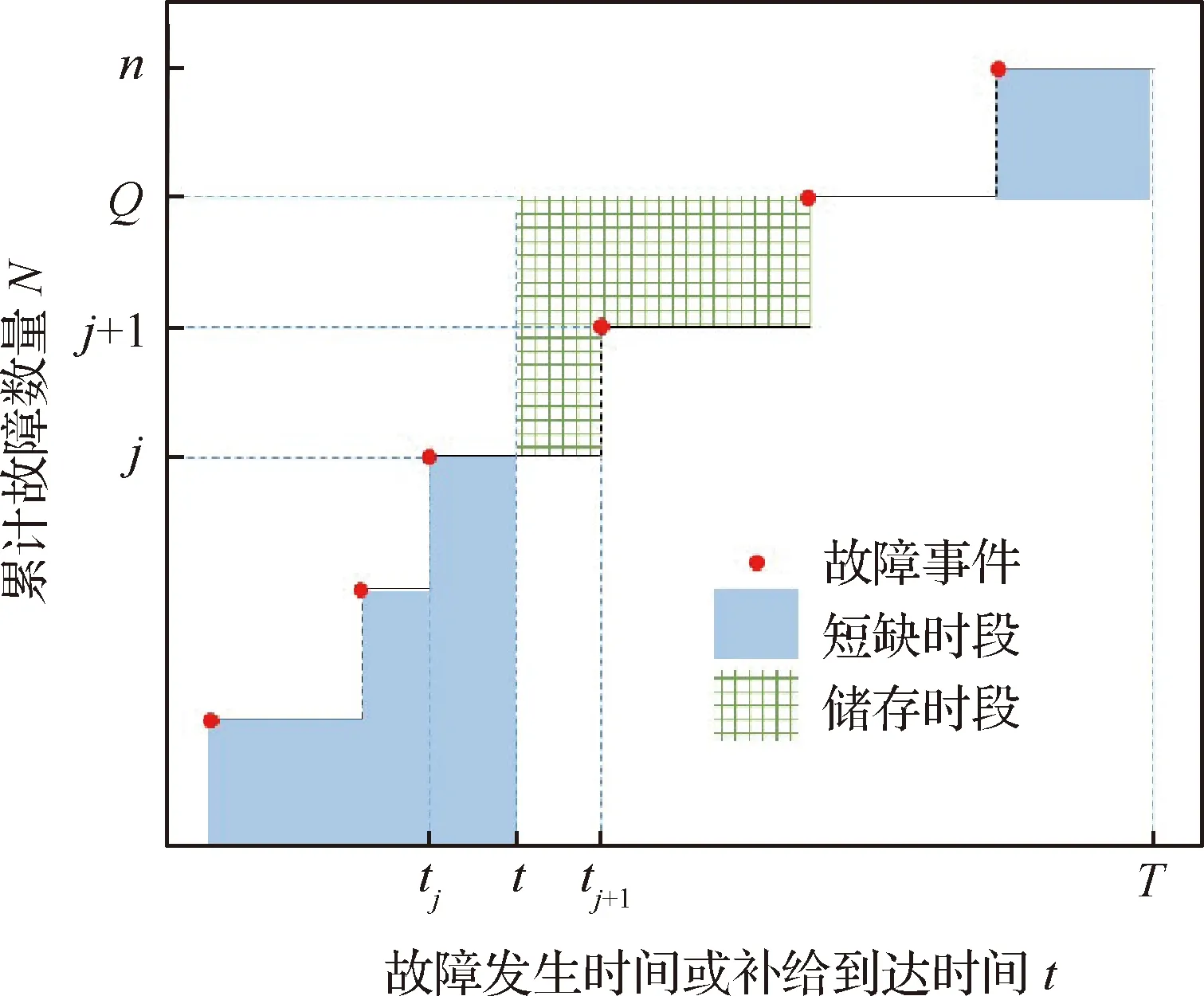
2 立方星可靠性模型
2.1 立方星壽命數據
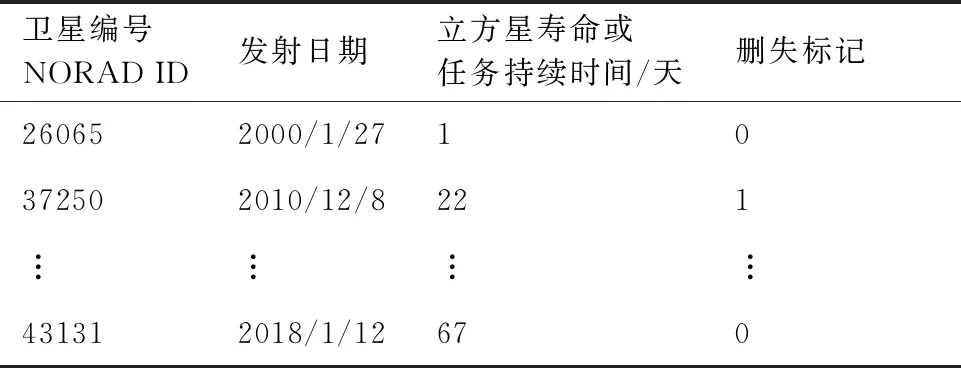
2.2 非參數分析
2.3 參數分析
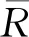
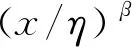
3 仿真方法
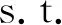
4 結果分析
4.1 立方星壽命分布模型

4.2 參數對總成本的影響
4.3 最優補給時刻與最優補給數量

4.4 不同可靠性模型對應的成本比較

4.5 早期、近期立方星補給策略對比
5 結 論

