基于空中交通密度的進場航班動態協同排序方法
劉繼新,江灝,*,董欣放,蘭思潔,王浩哲
1. 南京航空航天大學 民航學院,南京 211106 2. 國家空管飛行流量管理技術重點實驗室,南京 211106 3. 中國民用航空華北地區空中交通管理局天津分局,天津 300300
近年來,在全球經濟穩步復蘇,中國經濟運行穩中向好的態勢下,民航主要運輸指標保持平穩較快增長。2018年,民航全行業完成運輸總周轉量1 206.53億噸公里,比上年增長11.4%;全行業運輸航空公司完成運輸起飛架次469.47萬架次,比上年增長7.6%。以上數據表明,中國航空事業正快速發展,這使得航班數量日益增加,也增加了保障航班正常運行的壓力;同年全國客運航空公司共執行航班434.58萬班次,平均航班不正常率為19.87%,平均航班延誤時間為15 min[1]。
航班運行是嚴格基于管制員指令的,航班落地的時間依賴于管制員為其分配的次序。目前對進場航班的排序主要由管制員在熟悉各類航空器性能的基礎上,依據航班的動態信息與飛行計劃,依靠經驗進行。這種方法在任務繁重時,管制員的工作負荷較大、空管系統運行效率較低,且會導致大量的航班延誤。因此,空管部門希望在保證航班安全的前提下,盡量降低管制員的工作負荷。同時,航空公司和機場也基于自身利益,對進場航班排序提出了各自的要求:機場部門希望機場資源最大化的轉化為經濟效益并提高航班正常率;航空公司希望在保證市場公平性的前提下使得本公司的航班延誤最小。這樣,航班排序問題就變成多種因素耦合,復雜度急劇增高,先到先服務(First Come First Served, FCFS)的排序方法已經不能夠滿足航班排序的需要,這就需要使用更加科學合理的航班調度方法以滿足空管、航空公司和機場的訴求。
國內外相關學者從不同的角度對航班排序問題開展了大量研究,航班排序問題的研究主要集中于:動態調度、多跑道/多機場協同等。模型方面,文獻[2]基于滾動時域控制(Receding Horizon Control, RHC),將靜態調度推廣到動態調度領域。在RHC框架下,文獻[3-4]求解了多跑道機場的進場動態調度問題;文獻[5]建立了航班動態排序模型;文獻[6-8]從跑道協同的角度,實現進離場航班動態協同優化排序。文獻[9-10]引入多元受限時間窗的創新理念和航班滿意度概念,建立了多機場終端區進離場交通流協同排序模型。文獻[11-12]引入外圍航班流概念,建立了多機場終端區進離場航班協同優化排序模型。算法方面,遺傳算法[3-5,9-10]、分支定界法[6-8]、模擬退火算法[11-13]、蟻群算法[14]、貪心算法[15-16]、分散搜索算法和生態算法[17]等均被用來解決進場航班排序問題。目前國內外對于進場排序的研究成果較為豐富,部分已經應用于實際運行,如歐洲的進場管理(Arrival MANagement, AMAN)系統。但在下列研究領域中,仍有需要提升的空間:① 在實際運行過程,如何根據不同時段空中交通密度情況調整資源,選擇合理的優化目標與排序方案,在當前研究中尚有欠缺;② 在未來航空運輸業多方協同決策的發展趨勢下,當前研究未充分考慮空管、航空公司和機場對于進場航班排序的協同決策因素。
本文立足于民航運輸業多方協同決策的發展趨勢,以單跑道機場為對象,重點研究了不同空中交通密度下進場航班動態協同排序問題。研究工作著眼于進場航班排序的“動態性”和“協同性”。在滿足進場航班排序的“動態性”方面,基于進場航班的廣播式自動相關監視系統(ADS-B)數據,設計一種進場航班動態排序方法。本文的“協同性”是指在對進場航班排序時,充分考慮空管、航空公司和機場的訴求。這些將在以下內容中進行詳細闡述。
1 進場航班動態排序方法
為了滿足對進場航班排序的實時性和動態性要求,常用的策略是RHC,即每間隔一段時間對進場航班進行排序,從而實現對進場航班的連續排序過程。由于民航運輸業擁有大量可以獲得的運行數據,如雷達數據、ADS-B數據等,因此本文結合民航運輸業的運行特點,利用進場航班ADS-B數據中的航班號和航班實時位置信息,結合進場航班飛行計劃數據,設置相應的進場航班排序觸發及更新規則,作為實現航班實時、動態和自動化排序的基礎。
1.1 進場航班排序觸發及更新規則
進近管制區是連接區域管制區和機場塔臺管制區之間的空間。在實際運行中,對進場航班排序由進近管制員完成,進近管制員對進入進近管制區的進場航班進行排序,并通過調速、引導等手段實現預定次序。
本文模擬實際運行過程,設置以機場基準點為圓心的2個同心圓:起始圈和更新圈(如圖1所示),將更新圈內的范圍模擬成進近雷達管制區,起始圈和更新圈之間的范圍作為航班排序的緩沖區域,以使得進場航班在進入進近雷達管制區前即獲得落地次序,以便進近雷達管制員有充分的時間和充足的空間實現預定次序。起始圈和更新圈的構型亦可根據管制區的實際邊界形狀來確定。
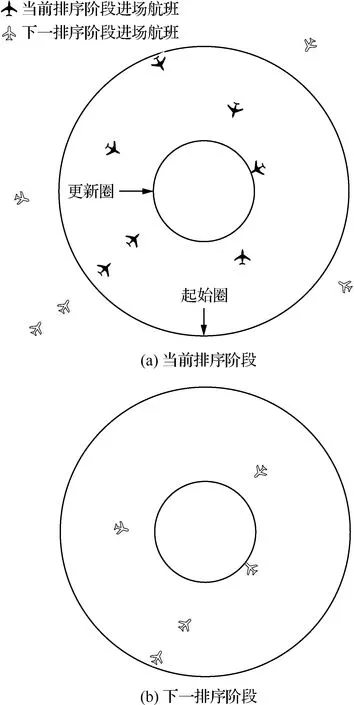
圖1 進場航班排序觸發及更新規則Fig.1 Rules for triggering and updating arrival flight sequencing
基于以上設置的進場航班排序起始圈和更新圈,結合ADS-B數據,設置一種進場航班排序觸發及更新規則:在當前排序階段,當第1架進場航班到達更新圈即觸發起始圈與更新圈之間的進場航班排序;以下一排序階段第1架進場航班到達更新圈作為排序更新觸發條件,對下一排序階段的進場航班進行新一輪排序從而實現對所有進場航班的連續排序。
1.2 起始圈和更新圈半徑的確定
1) 更新圈半徑R1
進近管制空域的水平范圍通常為半徑50 km或者走廊進出口以內的除機場塔臺管制區以外的空間[18]。因此,本文將更新圈的半徑R1設置為50 km。
2) 起始圈半徑R2
考慮到進近管制員應當有充足的空間和時間對各進場航班實施相應的管制方法,從而按照預定次序完成對進場航班的排序工作,故對進場航班落地次序的確定應當盡早完成。借鑒RHC中的排序時間窗概念,本文取15 min時間窗對應的航班飛行距離作為緩沖區域的長度。進場航班在接近進近管制區時的速度約為600 km/h,由此得到的緩沖區域長度為150 km,故將起始圈的半徑R2設置為200 km。
1.3 進場航班動態排序方法流程
本文提出的進場航班動態排序方法流程如圖2 所示。
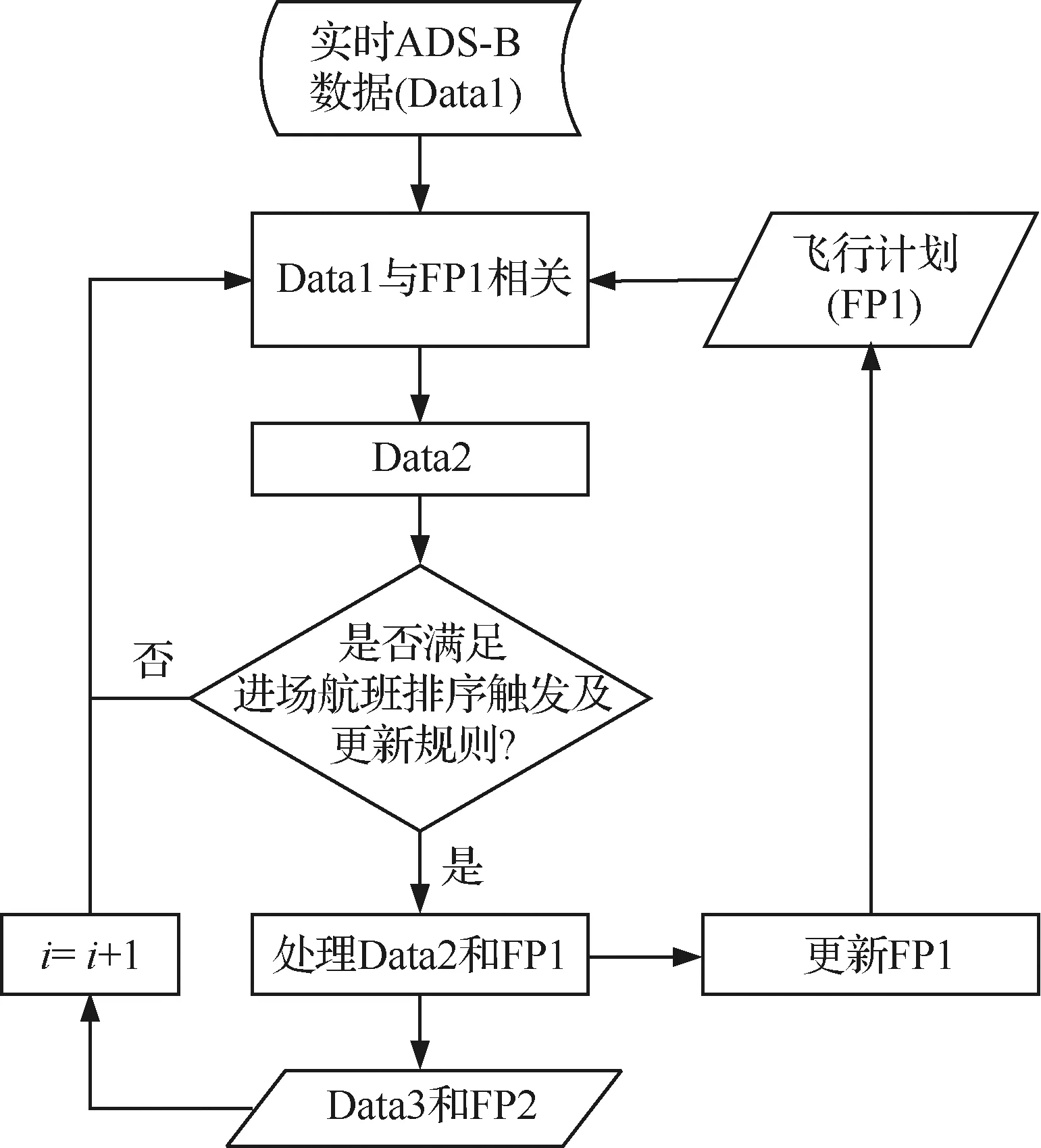
圖2 進場航班動態排序方法Fig.2 Dynamic sequencing method for arrival flights
步驟1將實時接收到的ADS-B數據(Data1)和本場進場航班飛行計劃(FP1)相關,篩選出本場進場航班的ADS-B數據(Data2)。
步驟2根據Data2中的航班位置信息,判斷是否滿足1.1節提出的進場航班排序觸發及更新規則,若滿足,則進行步驟3;若不滿足,則返回步驟1。
步驟3進一步處理Data2,篩選出此刻處于起始圈和更新圈之間的進場航班ADS-B數據(Data3),并從FP1中提取出Data3中涉及到的航班的飛行計劃數據(FP2)。輸出Data3和FP2作為后續對航班排序的初始輸入信息,并將FP2從FP1中刪除以完成對FP1的更新。
步驟4排序階段加1,返回步驟1。
2 模型建立
在CDM理念下對進場航班排序時,希望考慮到空管、航空公司和機場的訴求,但各方的目標眾多且一致性不強,甚至各目標之間會相互沖突,因此造成多目標進場航班排序問題的高復雜性。針對這一問題,本文以單跑道機場為例進行建模,提出一種基于空中交通密度的進場航班協同排序模型,從而滿足各方的定制化需求。
假設F為某日所有進場航班的集合;Fi為第i個排序階段的所有進場航班的集合。
2.1 目標函數
1) 跑道容量最大
本文考慮的最大化跑道容量,即某排序的最后一個進場航班的落地時間最小:
(1)
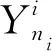
2) 航班延誤均衡性最高
本文綜合考慮航班總體延誤時間和個體延誤時間,提出航班延誤均衡性概念。本文將航班偏離計劃時刻當作延誤處理,則某排序階段內的航班延誤均衡性最高,即
(2)

3) 航班正常率最高
對進場航空器而言,航班正常判定標準為:不晚于計劃開艙門時間后10 min落地[19]。某排序階段內的所有進場航班正常率最高,即
maxWi
(3)

4) 航班延誤公平性最高
本文將航班延誤公平性以進場航班延誤時間均值和標準差來反映,因此某排序階段的進場航班延誤公平性最高,即進場航班延誤時間均值和標準差最小:
minAi
(4)
minσi
(5)
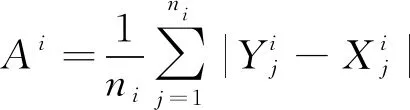
2.2 約束條件
本文提出的基于空中交通密度的進場航班協同排序模型,在管制間隔要求的基礎上,將其他運行約束與限制均轉化為時間窗約束。模型中涉及的約束條件如下。
2.2.1 管制間隔要求
由于進近管制員連續移交給塔臺管制員的進場航班高度通常為某一雙方約定的協議高度,故對于進場航班而言,其必須滿足水平間隔要求。當前進近管制單位多采用雷達管制,其中運行的進場航班在進近-塔臺移交點處受到的水平間隔約束有:雷達尾流間隔、雷達管制間隔和協議間隔。塔臺管制是有雷達設備的程序管制,塔臺管制下的進場航班落地前受到的水平間隔約束主要為非雷達間隔的尾流間隔。
1) 雷達尾流間隔
航空器在飛行過程中由于機翼上下表面的壓力差,會在翼尖處產生渦流,對后續飛行航空器的安全造成影響。因此,航班進場序列必須滿足尾流間隔要求,即
(6)
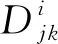
2) 雷達管制間隔
航班進場序列必須滿足雷達管制間隔要求,即
(7)
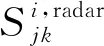
3) 協議間隔
航班進場序列必須滿足進近-塔臺移交的協議間隔要求,即
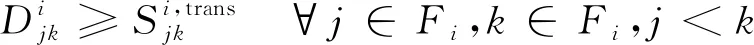
(8)
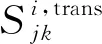
綜上,航班進場序列在進近-塔臺移交點處必須滿足管制間隔要求,即
(9)
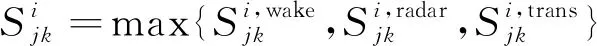
4) 非雷達間隔的尾流間隔
前后進近著陸的航班應能滿足非雷達間隔的尾流間隔要求,即
(10)
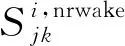
2.2.2 時間窗約束
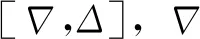
1) 可行著陸時間窗
終端空域范圍有限,考慮到航空器性能、燃油儲備、進場航線等因素的限制,為保證優化序列的可行性,優化序列中進場航班的計劃落地時間必須處于航班的可行著陸時間窗[E,L]內。
(11)
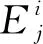
2) 可接受延誤時間窗
在管制運行過程中,管制員會根據不同類型進場航班的重要度,在進場排序時考慮其優先級。本文在文獻[9]的基礎上,建立進場航班類型和其可接受的最大提前/推遲到達時間之間的關系,從而得到進場航班可接受的延誤時間窗。
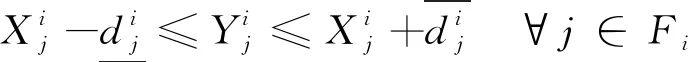
(12)

3) 管制負荷限制時間窗
管制員對于優化序列中與FCFS序列中次序偏差較大的航班,需要對其發布大量的附加指令,這會增加管制員的工作負荷。最大約束位置轉換(Maximum Position Shift, MPS)規定了優化序列中各航班次序相對于FCFS序列中相應航班次序的最大偏移量。由于航班次序的偏移也即航班到達時刻的偏移,因此,可以建立MPS約束和航班計劃落地時間之間的關系。基于以上分析,本文將MPS約束轉化為一種時間窗約束——管制負荷限制時間窗。
(13)

4) 公平性約束時間窗
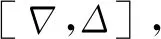
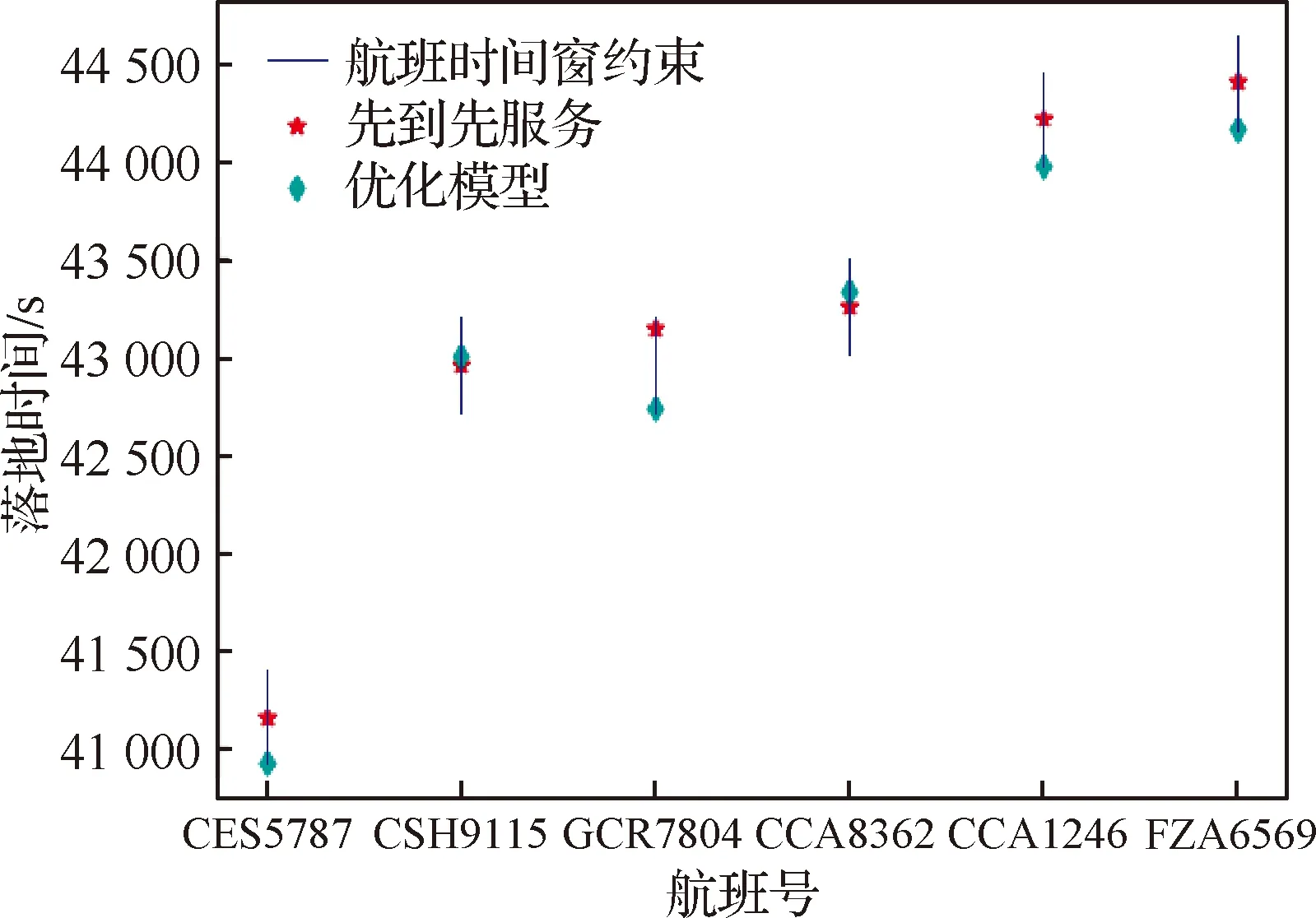
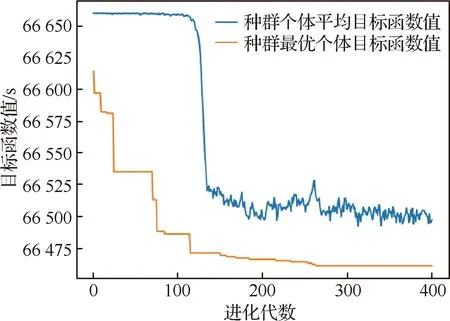
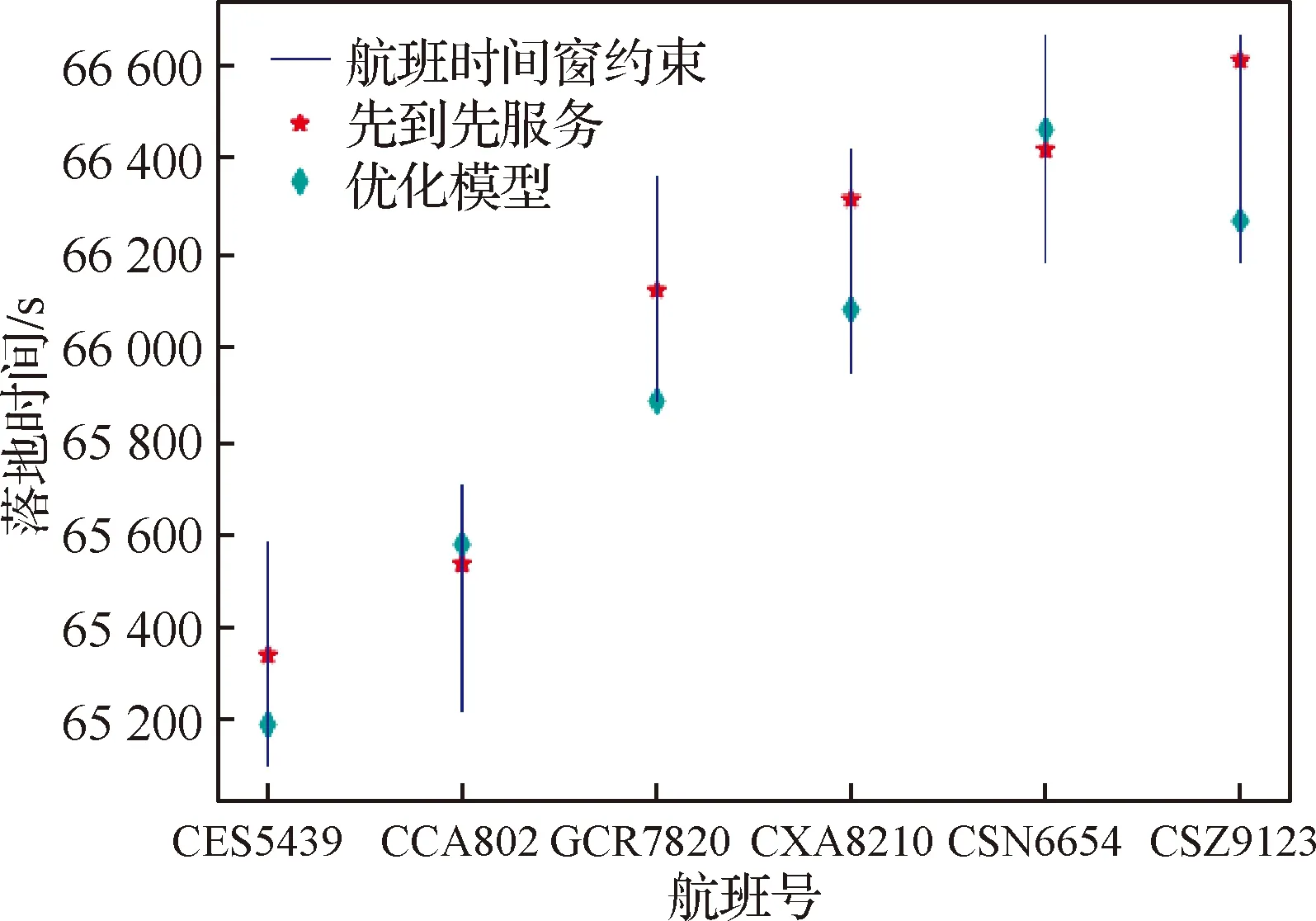
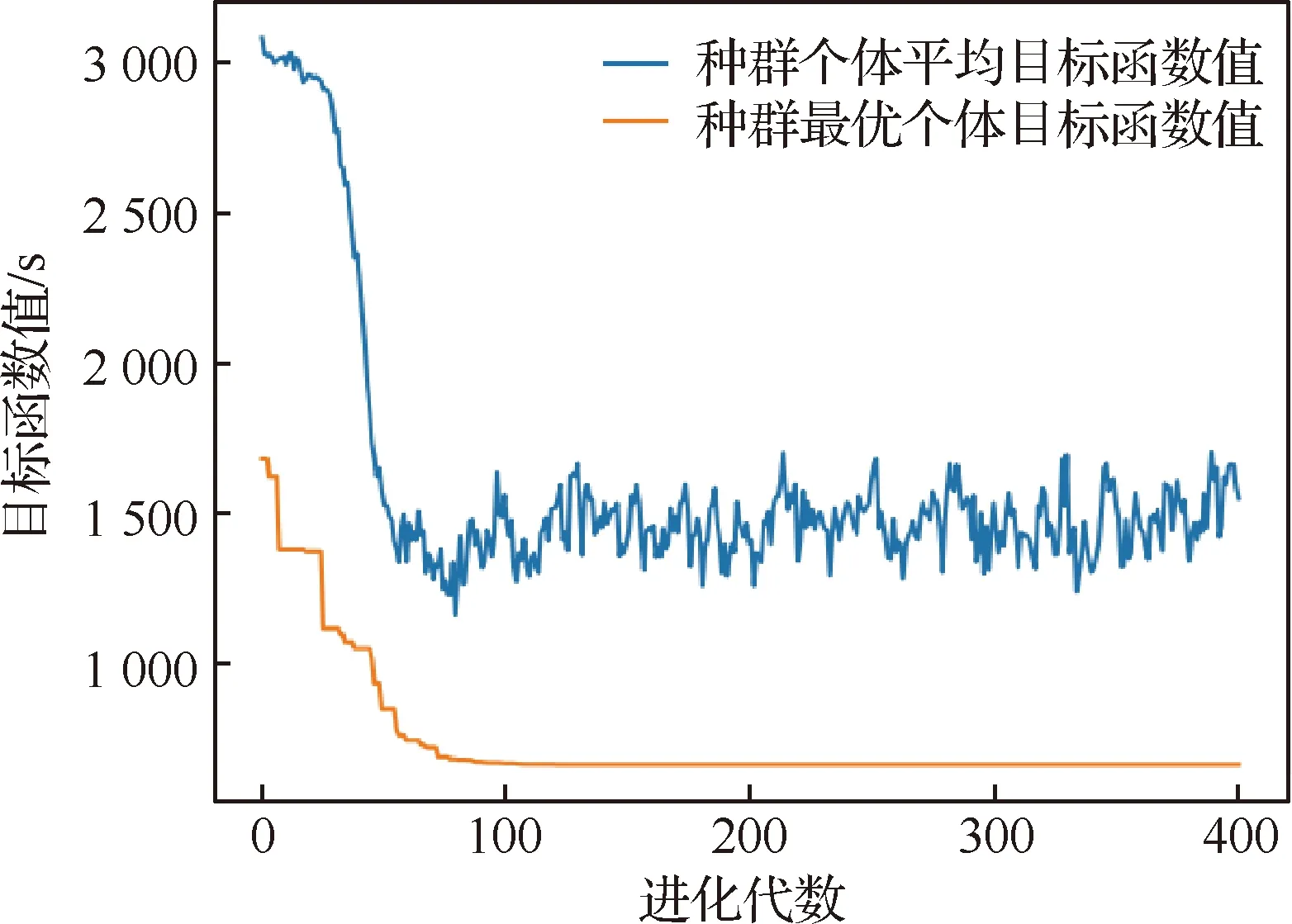
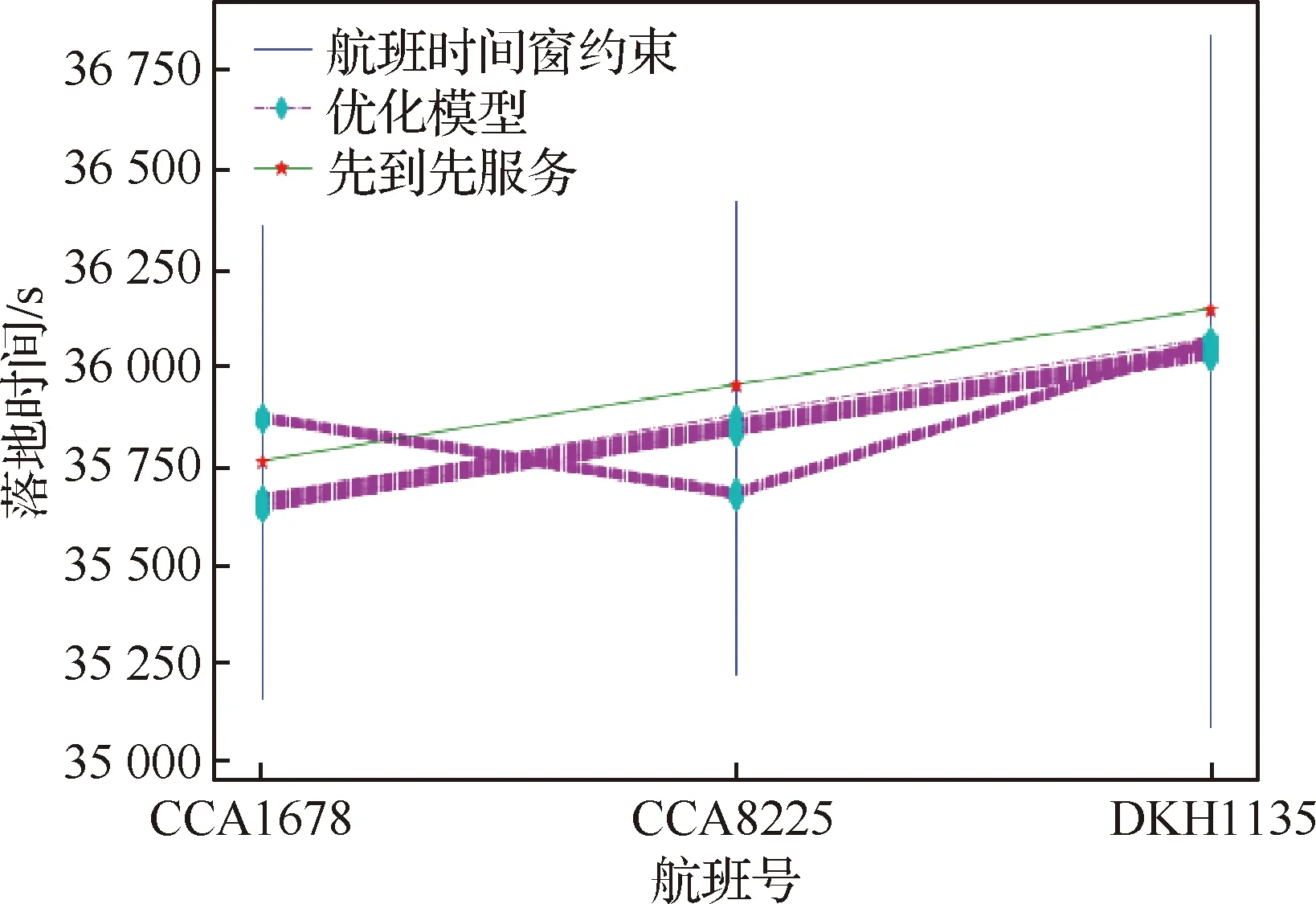
對于第i個排序階段使用同一進場航線的第j和k個進場航班(j 圖3 公平性約束時間窗調整Fig.3 Equity constraint time window adjustment 2.2.3 變量約束 目標函數及約束條件中涉及的各變量取值應滿足如下的約束: i,j,k,ni,ni,ot,K∈N (14) j,k,ni,ot≤ni (15) (16) 在CDM的理念下,應當充分考慮管制單位以外的航空公司和機場對于進場航班排序的決策因素。因此,本文設計了一種時隙交換方法以提高航空公司在進場航班排序過程中的參與度。 在實際運行中,航空公司從商業角度出發,基于對本公司的商業利益等多方面綜合考慮,對于航班的重要性分析與管制單位的分析存在差異。如:某個航班落地后有后續的飛行任務或者有較多落地機場換乘旅客,且前站已經延誤,航空公司為減小延誤損失,希望此航班盡快落地。時隙交換讓此設想成為可能。 2.3.1 時隙交換規則 本文涉及的時隙交換是指:在對進場航班進行優化排序后,航空公司在滿足航班可行著陸時間窗約束(式(11))的前提下,可對優化排序結果中分配給本公司航班的著陸次序進行再分配,犧牲本公司某個或某些進場航班的利益以優先保障重要進場航班,從而提高決策的科學性和合理性。 考慮到尾流間隔的不對稱性,為使得交換時隙后不影響其他公司的航班,保證航空公司間的公平性,本文設計的時隙交換規則如下: 1) 同一航空公司同一尾流等級的進場航班之間。 或者 2) 在不影響其它航空公司航班時,同一航空公司不同尾流等級的進場航班之間。 2.3.2 時隙交換方法流程 基于本文2.3.1節設計的時隙交換規則,本文的時隙交換方法實施步驟如下: 步驟1根據實時排序結果和2.3.1節時隙交換規則,確定可進行時隙交換的航空公司及其對應的可發生時隙交換的航班。 步驟2向步驟1確定的各航空公司發送各自相應的可發生時隙交換的航班排序信息Seq1:航班號和初始落地次序。 步驟3各航空公司在收到Seq1后進行決策,向管制單位發送時隙交換后的航班排序信息Seq2。 步驟4將所有收到的Seq2進行整合并結合Seq1,獲得最終的排序結果。 基于空中交通密度的進場航班協同排序模型根據當前排序階段的空中交通密度高低,選擇相應的目標函數和約束條件對進場航班進行排序。在對空中交通密度大小進行分類時,主要考慮當前排序階段空中交通的擁擠程度,文獻[20]對歐洲、美國及日本的扇區交通流擁擠判定方法進行了比較分析,本文選取歐洲中央流量管理單位(Central Flow Management Unit, CFMU)的扇區流量黃色告警,即交通流量超過容量C的80%,作為判定空中交通密度高的標準;對于判定空中交通密度低的標準,本文設定為交通流量低于容量的50%。 通過以上分析,建立基于空中交通密度的進場航班協同排序模型如下: 1) 高密度(ni≥80%C) 此時,空中交通密度高,減輕管制負荷和提升跑道容量是當前最關注的問題。此時同時考慮的是空管和機場的利益,為減輕管制負荷,使用MPS約束并規定使用同一進場航線的進場航班間不允許超越;以當前排序階段內最后一個進場航班的計劃落地時間最小為目標,從而最大化跑道容量。即目標函數為式(1),約束條件為式(9)~式(13)。 2) 中密度(80%C>ni≥50%C) 此時,空中交通密度適中,管制員開始有一定的調配空間和時間,管制負荷不再是主要關注點,將航空公司的利益考慮進來,以航班延誤均衡性最高為目標。即目標函數為式(2),約束條件為式(9)~式(12)。 3) 低密度(ni<50%C) 此時,空中交通密度較低,管制員有充足的調配空間和時間,同時考慮航空公司和機場的訴求。從機場的角度出發,以航班正常率最高為目標;從航空公司角度,以航班延誤公平性最高為目標,并引入時隙交換方法滿足航空公司的定制化需求,從而實現三方協同排序。即目標函數為式(3)~式(5),約束條件為式(9)~式(12)。 進場航班動態協同排序問題具有多目標和多約束,屬于典型的非確定性多項式難解(Non-deterministic Polynomial-Hard, NP-Hard)問題。而遺傳算法作為經典的智能優化方法,其并不需要事先描述問題的全部特點及確定算法應采取的措施,由于其具有的此種健壯性,特別適合于處理傳統搜索算法解決不好的復雜和非線性問題。因此,本文采用精英保留的遺傳算法(EGA)[21]和帶精英策略的快速非支配排序遺傳算法(NSGA-II)分別對所建立的單目標和多目標模型進行求解。EGA和NSGA-II均使用了精英保留策略,此策略在種群進化過程中,保證了找到的最優解不會被拋棄,是群體收斂到優化問題最優解的一種基本保障。NSGA-II適用于求解復雜的多目標優化問題,其解決了NSGA的主要缺陷,具有快速、準確的搜索性能[22]。 所提算法的流程圖如圖4所示。 圖4 所提算法流程圖Fig.4 Flowchart of proposed algorithm 步驟1獲得本場進場航班的飛行計劃數據(FP1)和實時接收到的ADS-B數據(Data1)。 步驟2對FP1和Data1使用進場航班動態排序方法進行判斷,以確定是否觸發排序。若是,獲得Data3和FP2,并完成對FP1的更新,進行步驟3;否則,返回步驟1。 步驟3根據Data3和FP2,運用基于空中交通密度的進場航班協同排序模型獲得空中交通密度分類以及對進場航班排序的目標函數及約束;同時,此排序階段數據處理完成,返回步驟1進行后續的數據判斷及處理工作。 步驟4判斷空中交通密度分類。若是低密度,使用NSGA-II進行排序計算,獲得初步排序結果,時隙交換后獲得最終排序結果;若是中/高密度,使用EGA進行排序計算,獲得的排序結果即最終排序結果。 3.2.1 管制間隔處理 本文在對進場航班優化排序時綜合考慮雷達尾流間隔、雷達管制間隔、協議間隔和非雷達間隔的尾流間隔,并將基于距離的間隔要求進行空間—時間轉化,以獲得進場航班落地時間間隔要求。 情形1前機慢后機快(如圖5所示) 圖5 情形1 (前機慢后機快)Fig.5 Situation 1(trailing aircraft is faster than leading one) 此時進場航班在進近到落地過程中,接地點處二者的相對距離最小。 (17) 情形2前機快后機慢(如圖6所示) 圖6 情形2(前機快后機慢)Fig.6 Situation 2 (leading aircraft is faster than trailing one) 此時進場航班在進近到落地過程中,進近-塔臺移交點處二者的相對距離最小。 (18) 綜上,進場航班的落地時間應當滿足: (19) 3.2.2 時間窗處理 1)可接受的最大提前/推遲到達時間 本文考慮機場和航空公司雙方的訴求,將機場基地航空公司航班的重要度設置為次高等級。 2) 單位時間偏移量 3.2.3 遺傳算法編解碼 本文在進行模型求解時將以時分形式表示的時間均轉換成用秒表示,即將a時b分轉換成秒的轉換公式為:a×3 600+b×60。 本文采用實數編碼的方式對進場航班的計劃落地時間進行編碼。根據2.2.2節確定的航班時間窗約束,第i個排序階段第j個進場航班的計劃落地時間編解碼公式為 (20) 天津濱海國際機場(ZBTJ)擁有平行雙跑道并采用隔離平行運行模式,其中僅有東跑道用于落地,其適用于本文提出的優化排序模型。因此,本文以天津濱海國際機場為例,對某日某時段的進場航班進行動態協同排序。 綜合考慮算法運行時間和收斂效果,多次調整參數取值并進行仿真實驗,獲得對于進場航班排序問題有效的算法參數如下: 1) EGA控制參數包括:種群規模為100;最大進化代數為400;染色體編碼長度為ni;采用兩點交叉,交叉概率為1;采用實值變異,利用壓縮率和梯度劃分來控制變異距離,壓縮率為0.5,梯度為20。 2) NSGA-II控制參數包括:種群規模為200;最大進化代數為500;染色體編碼長度為ni;采用模擬二進制交叉和多項式變異,交叉和變異概率均為1,分布指數為20。 本文將基于RHC策略的動態排序方法(簡稱RHC方法)、基于先到先服務策略的排序方法(簡稱先到先服務方法)與所提的基于空中交通密度的進場航班動態協同排序方法(簡稱動態協同方法)進行對比,以評估所提方法的優化效果。本文選擇某日2個不同時段,共對165架次(時段1∶82架次、時段2∶83架次)進場航班進行排序。 4.2.1 RHC方法與動態協同方法對比 本文設定RHC的排序時間窗為30 min,滑動時間窗為15 min。圖7為RHC方法對時段1的不同排序開始時間(7∶30、7∶35和7∶40)和時段2的不同排序開始時間(16∶25、16∶30和16∶35),每次排序時涉及的航班個數及其在排序時段內出現的次數統計。由圖7可見,RHC方法對于不同的排序開始時間會獲得不同的結果,因此RHC方法結果無法反映空域系統的實時狀態,進而準確判定實時的空中交通密度情況。而動態協同方法基于航空器實時位置信息觸發排序,所得結果與排序開始時間無關。 圖7 RHC方法在不同排序開始時間情況下的結果對比Fig.7 Results comparison of RHC method with different starting time of sequencing 圖8為RHC方法和動態協同方法每次排序時涉及的航班個數及其在排序時段內出現的次數統計。由圖8可見,對于時段1(時段2),RHC方法共進行了36次(36次)排序,動態協同方法共進行了28次(25次)排序,減少了8次/22.2%(11次/30.6%)。因為在對進場航班排序時不希望出現無航班需進行排序和僅有1個航班需進行排序的情況,故出現此2種情況的次數越少,排序的效率越高。對于時段1(時段2),RHC方法存在4次(4次)無航班需進行排序和10次(9次)僅有1個航班需進行排序的情況,而動態協同方法不存在無航班需進行排序和存在4次(3次)僅有1個航班需進行排序的情況,排序效率有所提高。 圖8 RHC方法和動態協同方法結果對比Fig.8 Comparison of results between RHC method and dynamic collaborative method 4.2.2 先到先服務方法與動態協同方法對比 在時段1(時段2)內,動態協同方法共包括28個(25個)排序階段:高密度2個(2個),中密度6個(10個),低密度20個(13個)。仿真結果表明,各密度條件下算法運行時間均小于1 s,且隨著遺傳算法進化代數的增加,各密度條件下種群中的個體均朝著最優化方向進化,故其能快速獲得最優解。較先到先服務方法,對時段1(時段2)而言,高密度條件下各排序階段最后一個進場航班的落地時間平均提前203.5 s(196 s);中密度條件下各排序階段航班延誤總時間平均減少30.8%(27.4%),航班延誤均衡性平均提高35.5%(31.9%);低密度條件下在航班正常率及航班延誤公平性得到保證的前提下,滿足時隙交換規則的排序階段均增加了1種進場航班排序模式。 以下對各交通密度條件下,使用先到先服務方法和基于空中交通密度的進場航班協同排序模型(以下簡稱優化模型)的排序結果作詳細的對比討論。 1) 高密度 圖9為時段1第11個排序階段最后1個進場航班的落地時間(優化目標1)在不同進化代數對應的種群個體平均目標函數值和最優個體目標函數值的變化趨勢。從圖中可以看出,隨著種群的不斷進化,種群個體的平均和最優目標函數值變化趨勢一致,均朝著優化的方向變化。從種群最優個體目標函數值曲線中可以看出,在50代以內,最優目標函數值迅速由44 292 s下降到44 173 s 后不再發生變化。從種群個體平均目標函數值曲線中可以看出,種群的平均目標函數值迅速由44 624 s下降到44 200 s后趨于穩定,種群收斂。 圖9 種群進化過程中目標函數值變化趨勢(時段1-11)Fig.9 Trend of objective function value in population evolution process (time interval 1-11) 圖10為時段1第11個排序階段優化模型排序結果與先到先服務排序結果的對比。由圖可見,相對于先到先服務排序結果,優化模型排序結果中的CSH9115落地次序推遲,GCR7804落地次序提前,且次序變化量都為1,此結果驗證了本文將MPS約束轉化為管制負荷限制時間窗的可行性。先到先服務排序結果最后一個進場航班的落地時間為44 413 s,優化模型排序結果為44 173 s,落地時間提前了240 s,即對于此排序階段可多容納2架進場航班落地。 圖10 不同策略下進場航班計劃落地時間(時段1-11)Fig.10 Scheduled landing time of arrival flights using different strategies (time interval 1-11) 圖11為時段2第6個排序階段最后一個進場航班的落地時間(優化目標1)在不同進化代數對應的種群個體平均目標函數值和最優個體目標函數值的變化趨勢。從圖中可以看出,隨著種群的不斷進化,種群個體的平均和最優目標函數值變化趨勢一致,均朝著優化的方向變化。從種群最優個體目標函數值曲線中可以看出,在150代以內,最優目標函數值迅速由66 618 s下降到66 471 s;在150代~263代,最優目標函數值由66 471 s平緩的下降到66 461 s;263代以后,最優目標函數值不再發生變化。從種群個體平均目標函數值曲線中可以看出,種群的平均目標函數值迅速由66 664 s下降到66 500 s后趨于穩定,種群收斂。 圖11 種群進化過程中目標函數值變化趨勢(時段2-6)Fig.11 Trend of objective function value in population evolution process (time interval 2-6) 圖12為時段2第6個排序階段優化模型排序結果與先到先服務排序結果的對比。由圖可見,相對于先到先服務排序結果,優化模型排序結果中的CSN6654落地次序推遲,CSZ9123落地次序提前,且次序變化量都為1,此結果同樣驗證了本文將MPS約束轉化為管制負荷限制時間窗的可行性。先到先服務排序結果最后一個進場航班的落地時間為66 613 s,優化模型排序結果為66 461 s,落地時間提前了152 s,即對于此排序階段可多容納1架進場航班落地。 圖12 不同策略下進場航班計劃落地時間(時段2-6)Fig.12 Scheduled landing time of arrival flights using different strategies (time interval 2-6) 可見,在高密度條件下,使用優化模型排序方法可使得最后一個進場航班的落地時間提前,進而實現提升跑道容量的目標。 2) 中密度 圖13為時段1第6個排序階段內的航班延誤均衡性(優化目標2)在不同進化代數對應的種群個體平均目標函數值和最優個體目標函數值的變化趨勢。從圖中可以看出,隨著種群的不斷進化,種群個體的平均和最優目標函數值變化趨勢一致,均朝著優化的方向變化。從種群最優個體目標函數值曲線中可以看出,在90代以內,最優目標函數值迅速由1 743 s下降到672 s;在90代至121代,最優目標函數值由672 s平緩的下降到656 s;121代以后,最優目標函數值不再發生變化。從種群個體平均目標函數值曲線中可以看出,種群的平均目標函數值迅速由3 078 s下降到1 280 s后趨于穩定,種群收斂。 圖13 種群進化過程中目標函數值變化趨勢(時段1-6)Fig.13 Trend of objective function value in population evolution process (time interval 1-6) 圖14為時段1第6個排序階段優化模型排序結果與先到先服務排序結果的對比。由圖可見,先到先服務排序結果和優化模型排序結果各航班落地次序相同。先到先服務排序結果的所有進場航班延誤總時間為765 s,優化模型排序結果的所有進場航班延誤總時間為481 s,減少了284 s (37.1%);先到先服務排序結果的航班延誤均衡性為1 100 s,優化橫型排序結果的航班延誤均衡性為656 s,提高了444 s(40.4%)。對具體的航班而言,先到先服務排序結果中后3架航班均發生延誤,分別為CDG4801延誤142 s、CCA8128延誤335 s、CXA8033延誤288 s。由于CDG4801的尾流等級為中級,而在其前落地的KAL805的尾流為重級,因此二者之間需要滿足較大的間隔要求,后續落地的CCA8128和CXA8033均存在較大延誤的原因是CDG4801延誤的傳遞。優化排序結果中KAL805和CDG4801分別提前 175 s 和33 s,CCA8128和CXA8033分別推遲160 s和113 s,優化排序結果中前機提前落地,減弱了前機延誤對后機的影響,在一定程度上避免了延誤的傳遞,可見優化排序結果將延誤均衡化。 圖14 不同策略下進場航班計劃落地時間(時段1-6)Fig.14 Scheduled landing time of arrival flights using different strategies (time interval 1-6) 圖15為時段2第18個排序階段內的航班延誤均衡性(優化目標2)在不同進化代數對應的種群個體平均目標函數值和最優個體目標函數值的變化趨勢。從圖中可以看出,隨著種群的不斷進化,種群個體的平均和最優目標函數值變化趨勢一致,均朝著優化的方向變化。從種群最優個體目標函數值曲線中可以看出,在50代以內,最優目標函數值迅速由714 s下降到206 s;在39代至159代,最優目標函數值由206 s平緩的下降到200 s;159代以后,最優目標函數值不再發生變化。從種群個體平均目標函數值曲線中可以看出,種群的平均目標函數值迅速由3 044 s下降到638 s后趨于穩定,種群收斂。 圖15 種群進化過程中目標函數值變化趨勢(時段2-18)Fig.15 Trend of objective function value in population evolution process (time interval 2-18) 圖16為時段2第18個排序階段優化模型排序結果與先到先服務排序結果的對比。由圖可見,先到先服務排序結果和優化模型排序結果各航班落地次序相同。先到先服務排序結果和優化模型排序結果所有進場航班延誤總時間均為133 s,但較先到先服務排序結果航班延誤均衡性266 s,優化模型模型排序結果航班延誤均衡性為200 s,提高了66 s(24.8%)。對具體的航班而言,先到先服務排序結果中僅CSC8128延誤133 s;優化模型排序結果中OKA3084提前67 s,CSC8128推遲66 s,可見優化模型排序結果將延誤均衡化。 圖16 不同策略下進場航班計劃落地時間(時段2-18)Fig.16 Scheduled landing time of arrival flights using different strategies (time interval 2-18) 在實際管制運行中,當2架進場航班間隔過小時,管制員通常使用“前快后慢”的方法拉開間隔,因此優化模型排序結果符合實際運行情況。在中密度條件下,優化模型排序結果均衡了總體延誤和個體延誤,并貼近實際運行,使用優化模型排序方法可有效提高延誤均衡性。 3) 低密度 由于目標函數和約束條件可相互轉換,本文在求解模型時將目標函數(3)轉換為航班正常率為1的約束。 圖17為時段1第5個排序階段內的進場航班延誤時間均值(優化目標4)和標準差(優化目標5)在種群進化完成時所得的Pareto最優解。 圖17 Pareto最優解(時段1-5)Fig.17 Pareto optimal solution (time interval 1-5) 圖18為時段1第5個排序階段優化模型排序結果與先到先服務排序結果的對比。可知,優化模型排序結果提供了2種排序模式:① 與先到先服務排序結果相同;② 較先到先服務排序結果,CCA1678和CCA8225的落地次序互換。此優化結果保證了時隙交換的可行性,對國航而言,由于CCA1678和CCA8225的尾流等級均為中級,其可根據實際需要選擇是否交換二者的落地次序。 圖18 不同策略下進場航班計劃落地時間(時段1-5)Fig.18 Scheduled landing time of arrival flights using different strategies (time interval 1-5) 圖19為時段2第8個排序階段內的進場航班延誤時間均值(優化目標4)和標準差(優化目標5)在種群進化完成時所得的Pareto最優解。由圖可見,此排序階段僅存在1個Pareto最優解,即算法尋找到對于優化目標4和優化目標5均為最優的解。該最優解表明,此排序階段的所有航班均無延誤發生。 圖19 Pareto最優解(時段2-8)Fig.19 Pareto optimal solution (time interval 2-8) 此階段的進場航班為GCR7826和GCR7896,二者尾流等級為中級和重級,但由于此階段的航班均屬于同一航空公司,故滿足時隙交換規則的要求。對天航而言,其可根據實際需要選擇是否交換GCR7826和GCR7896的落地次序,若選擇交換落地次序,則GCR7896最多可提前10分鐘落地。因此,使用時隙交換方法的優化模型排序結果提供了2種排序模式:①與先到先服務排序結果相同;②較先到先服務排序結果,GCR7826和GCR7896的落地次序互換。圖20為時段2第8個排序階段優化模型排序結果與先到先服務排序結果的對比。 可見,低密度條件下,在航班正常率及航班延誤公平性得到保證的前提下,進場航班排序的靈活性提高,實現了三方協同排序。 在理論層面上,本文基于以往的研究,所做的改進與主要區別如下: 1) 文獻[9-10]對某一時段內的所有航班進行排序,執行一次算法的時間均超過10 min,排序的實時性稍差。本文基于進場航班ADS-B數據和飛行計劃數據,設計了一種進場航班動態排序方法,將某一時段劃分為多個排序階段,并且在各排序階段內算法運行時間均小于1 s,實現了進場航班實時、動態和自動化排序。 2) 文獻[9]提出了“多元受限時間窗”的概念,本文在此基礎上進行改進:① 在可接受延誤時間窗中,考慮機場和航空公司雙方的訴求,將機場基地航空公司航班的重要度設置為次高等級;② 提出了“管制負荷限制時間窗”的概念,建立了MPS約束和航班計劃落地時間之間的關系。 3) 文獻[9-10]均使用了航班延誤總時間最小作為目標函數之一,本文提出“航班延誤均衡性”的概念,綜合考慮航班總體延誤時間和個體延誤時間,將航班總體和個體延誤均控制在較低水平。 在實踐應用層面上,本文基于以往的研究,所做的改進如下: 1) 本文深入分析管制運行特性,充分考慮管制負荷對進場航班排序的影響,對空中交通密度進行分類,在各密度條件下選擇合理的優化目標與排序方案,建立了基于空中交通密度的進場航班協同排序模型。 2) 在管制運行中優先保障重要度高的航班,其通常提前到達,但不可推遲到達;重要度低的航班可提前亦可推遲到達。基于此,本文將文獻[9]的“最大可接受延誤時間”細化,提出“可接受的最大提前到達時間”和“可接受的最大推遲到達時間”。 3) 在實際運行中,航空公司從商業角度出發,基于對本公司的商業利益等多方面綜合考慮,對于航班的重要性分析與管制單位的分析存在差異。因此在CDM的理念下,本文設計了一種時隙交換方法以充分考慮航空公司對于進場航班排序的決策因素。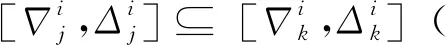
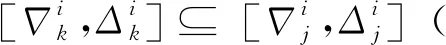

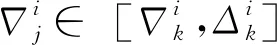
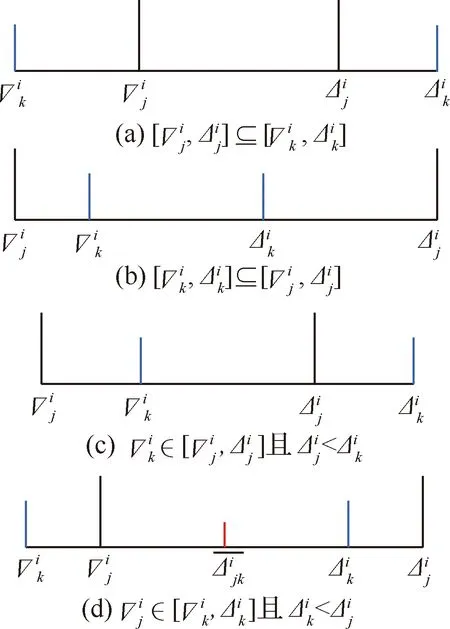

2.3 時隙交換方法
2.4 基于空中交通密度的進場航班協同排序模型
3 算法設計
3.1 算法流程

3.2 算法實現
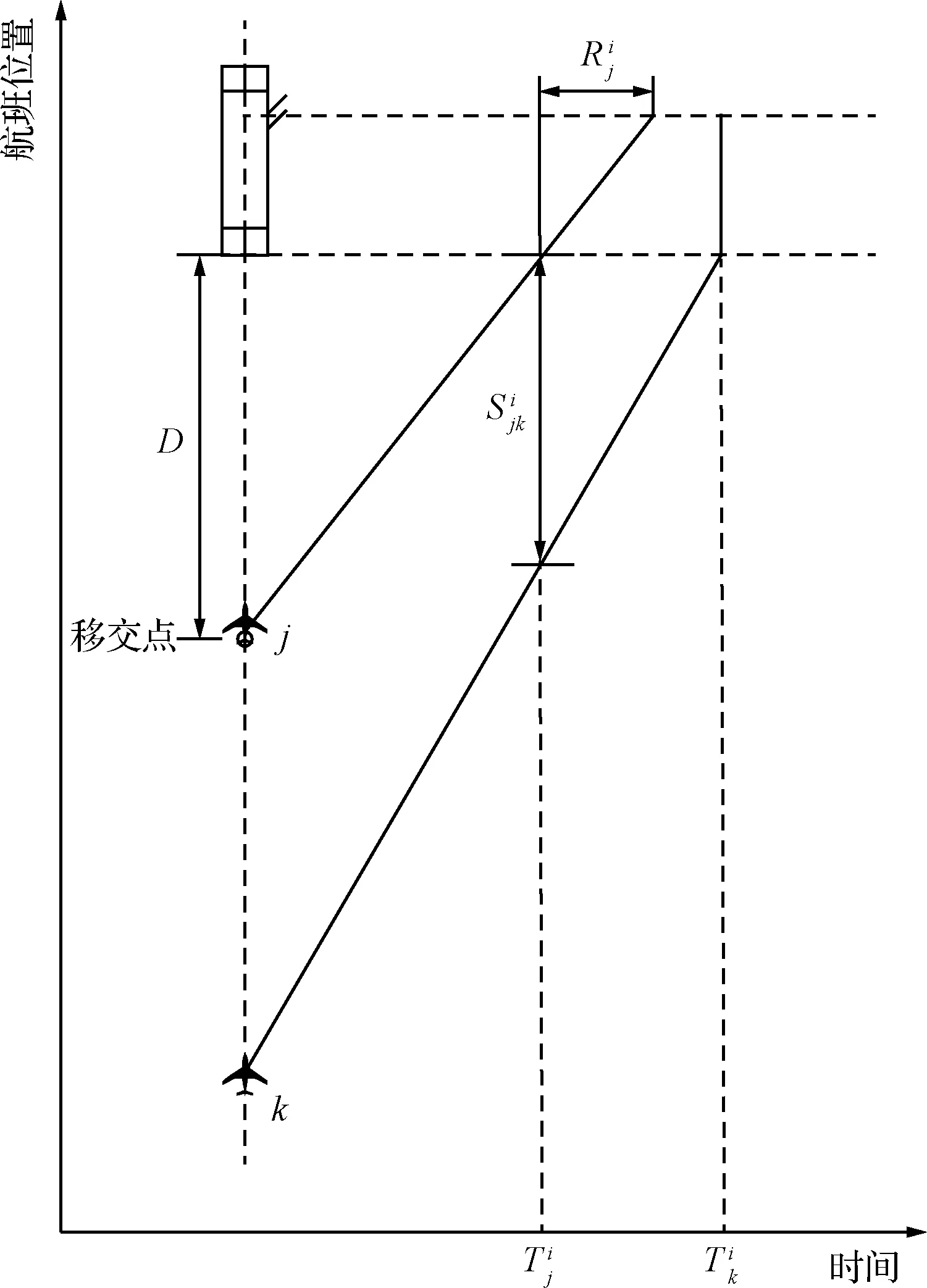


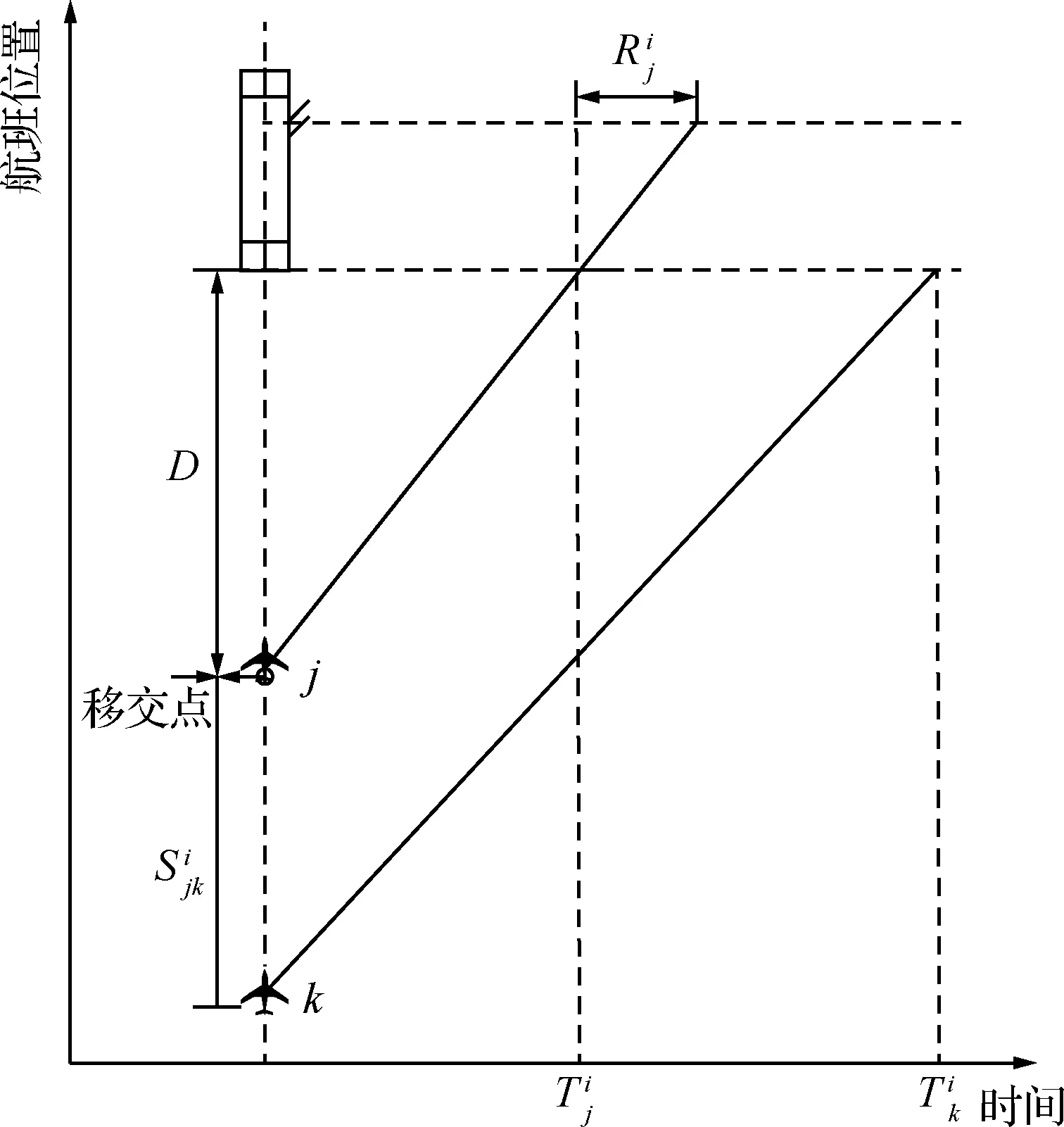

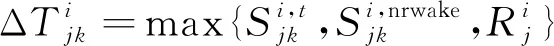
4 實例驗證
4.1 實驗設計
4.2 結果分析







5 結 論

