考慮多重影響因素的巡航飛行器增程優化設計研究

張嘉良　秦偉偉　秦慶強　鄭帥　劉剛

摘要：? ? ? 為有效提升現有巡航飛行器的航程， 在不改變飛行器總體布局的情況下， 考慮氣動特性、 質量等多重因素影響， 研究了某巡航飛行器增程優化技術。 首先， 分析了巡航飛行器在典型飛行任務下的氣動特性以及優化所需的有效參數; 其次， 構建了機翼翼展變化時翼展長度與機翼面積的映射模型， 估算了不同翼展長度情況下飛行器質量的變化; 然后， 以翼展長度作為直接設計變量， 考慮計算精度與優化效率， 設計了基于遺傳算法與神經網絡相結合的優化方法， 完成特定飛行條件下的航程優化。 仿真分析表明， 在設計約束范圍內， 當翼展長度增加到原來的1.16倍時， 其航程相比原來可以增加18.03%， 達到性能最優， 同時， 將影響航程變化的質量要素納入設計優化， 提高了性能優化的精準性。 本文方法具有一定的理論和應用價值。

關鍵詞：? ? ?巡航飛行器; 增程優化; 質量特性; 翼展變化

中圖分類號：? ? ? V212文獻標識碼：? ? A文章編號：? ? ?1673-5048（2020）02-0032-07

0引言

機翼設計在飛行器的氣動布局及總體設計中有著極其重要的地位[1-2]， 合理的翼形結構、 外形設計可以使飛行器具備良好的氣動、 飛行性能[3-4]。 所以飛行器的優化設計通常是從飛行器的任務需求、 性能要求出發， 對其結構、 外形以及重要飛行參數進行相應的探索， 進而給出具體的設計參考[5]。 例如， 王江華等[6]提出了分級伸縮翼構型， 優化計算了在相應飛行任務中不同伸縮構型， 降低了導彈燃料消耗的效能; 張公平等[7]對可變形翼戰術導彈的氣動特性進行深入研究， 提出了一種可同時兼顧可用過載與射程的優化方法; 張登成等[8]針對在寬速域內飛行器的氣動特性要求， 設計了變構型超聲速飛行器， 在保證良好氣動性能的前提下提升了低/跨/超聲速性能; 馬洋等[9]針對多任務、 全速域飛行要求， 提出了一種基于升力體的變構型超聲速飛行器。 可見， 改變翼形、 機翼結構等方法[10-11]， 對于改善飛行器氣動特性、 提升飛行器性能指標等方面有著顯著的優勢， 在飛行器的優化設計中越來越受到研究者的重視。

然而， 變翼形、 變結構不僅會引起飛行器展弦比、 浸濕面積等外形參數的變化， 也會使機身自重發生改變， 進而影響到航程、 續航時間、 燃料消耗等關鍵性能參數[12]。 因此， 在進行優化設計時， 有必要考慮質量變化的影響， 但是目前很少有文獻考慮相關方面的問題。 為此， 本文以亞聲速巡航飛行器為背景， 重點考慮在優化設計時機翼質量因素、 面積因素以及具體的參數約束等多重約束特性影響， 建立質量估計模型， 研究翼展的改變對某飛行器氣動特性以及航程的影響， 進而提出優化設計方法， 實現在給定設計約束條件下的航程優化。

1研究背景

基于翼展、 翼面積可變的概念， 對機翼進行優化設計。 保持飛行器的基本氣動布局、 最大起飛重量不變， 并保持機翼翼型不變， 概念示意圖如圖1所示。

在一定范圍內改變機翼的翼展長度、 探索翼展的變化對飛行器氣動性能、 以及對其航程的影響， 通過優化使得航程達到最大， 進而設計最佳增程方案。 關于航程的最初評估可以由Breguest航程公式[13-14]得到：

式中： R為飛行器在某特定飛行狀態下一段時間內的航程; v為飛行速度; ρ為空氣密度; g為重力加速度; c為比沖的倒數; m1， m2分別為初始時總質量和消耗燃料后的總質量; S為參考面積; CD0和k分別為零升阻力系數和升致阻力系數[15]。

由此可見， 從翼展長度的角度進行優化設計， 參數主要有翼展改變后具體飛行條件下飛行器的升阻力系數、 機翼面積以及機翼質量隨翼展長度變化的近似參數模型。

2氣動特性分析

首先， 由實際的外形參數、 氣動布局對巡航飛行器進行建模、 劃分網格， 然后進行CFD氣動仿真。 選取實際飛行條件下的工況進行數值計算： 馬赫數漸次取Ma=0.68～0.78， 以機身長度為參考長度確定流動雷諾數Re=1.07×107， 粘性系數μ的計算采用Sutherland公式， 并且假設來流滿足理想氣體方程。 攻角取4°～5.5°。 選取SST k-ω湍流模型進行粘性效應的模擬， 計算采用高精度的AUSM二階迎風格式。 計算網格的劃分和仿真結果云圖如圖2～3所示。

航空兵器2020年第27卷第2期張嘉良， 等： 考慮多重影響因素的巡航飛行器增程優化設計研究圖2計算網格

相同工況下使用Missile Datcom進行計算， 并繪圖對比了兩種計算方式所得數據結果， 如圖4～5所示。

由對比圖可見， 飛行器在以小攻角、 高亞聲速工況下飛行時， 其升阻比可達到最大。 在該飛行工況下改變翼展長度， 并繪制升阻比與阻力系數隨翼展增加的變化曲線， 如圖6所示。

3面積與質量估算模型

3.1機翼面積計算模型

機翼俯視面近似為梯形， 由原始設計參數可以獲得機翼的翼形、 根弦長度、 展弦比， 前緣后掠角及翼根厚度。 假設機翼沿翼展長度方向均勻伸長， 且前緣后掠角、 1/4弦線后掠角保持不變， 機翼翼展變化示意如圖7所示。

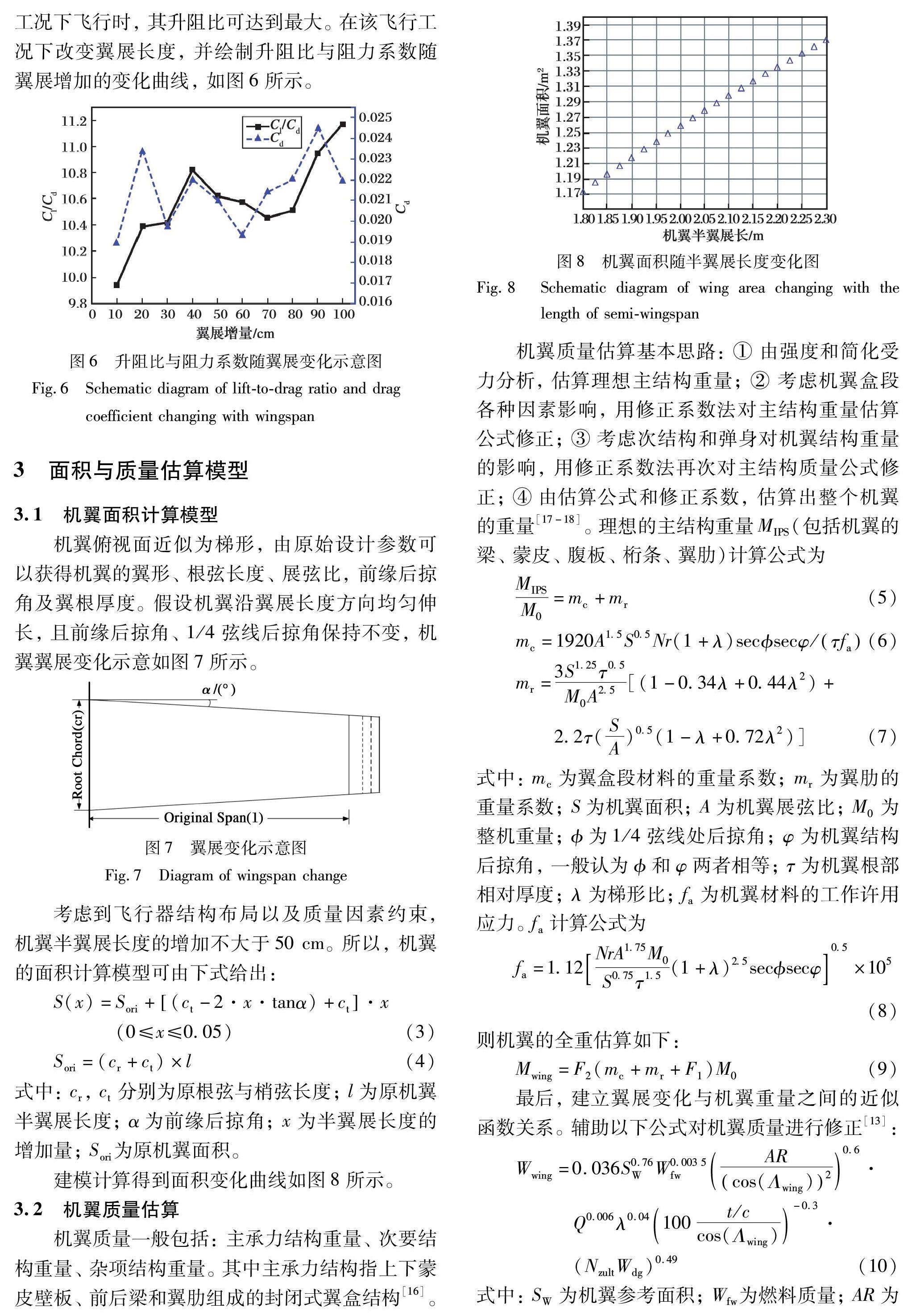
建模計算得到面積變化曲線如圖8所示。

3.2機翼質量估算

機翼質量一般包括： 主承力結構重量、 次要結構重量、 雜項結構重量。 其中主承力結構指上下蒙皮壁板、 前后梁和翼肋組成的封閉式翼盒結構[16]。

機翼質量估算基本思路： ① 由強度和簡化受力分析， 估算理想主結構重量; ② 考慮機翼盒段各種因素影響，? 用修正系數法對主結構重量估算公式修正; ③ 考慮次結構和彈身對機翼結構重量的影響， 用修正系數法再次對主結構質量公式修正; ④ 由估算公式和修正系數， 估算出整個機翼的重量[17-18]。 理想的主結構重量MIPS（包括機翼的梁、 蒙皮、 腹板、 桁條、 翼肋）計算公式為

4航程優化模型及算法

4.1優化模型

本文的優化目標是在翼展變化范圍內使航程達到最大。 根據航程公式， 速度、 比沖等參數可直接由相關資料確定， 所以將直接受翼展變化影響的機翼質量W、 機翼面積S、 零升阻力系數CD0、 升致阻力系數K作為設計變量W，S，CD0，KT。 根據建立的估算模型及氣動分析數據， 可以進一步確定各設計變量的約束范圍。

4.2算法描述

由于所采用的航程經驗公式為復雜的多元非線性方程， 對于特定的計算任務， 為了盡可能保證估算結果的準確性， 考慮利用神經網絡的非線性擬合能力對航程計算結果進一步精確化， 然而神經網絡的權值與閾值一般是隨機初始化的， 通常會導致擬合結果不穩定。 常用的梯度下降法優化神經網絡會面臨網絡收斂速度較慢和容易陷入局部最優兩個問題， 所以， 先用遺傳算法對神經網絡初始權值和閾值進行優化， 構建較高精度的神經網絡模型， 再用樣本點數據及計算結果作為非線性函數的輸入輸出訓練神經網絡， 更好地預測輸出航程值。

要得到航程在設計翼展變化范圍內的最大值， 需要對擬合的非線性函數進行全局極值尋優， 所以， 再次用遺傳算法的快速尋優能力對訓練好的神經網絡的輸出結果進行極值尋優， 即用訓練后的神經網絡的預測結果作為個體適應度值， 通過選擇、 交叉、 變異等操作， 尋找函數的全局最優值及對應的輸入。 優化方法的整體流程如圖10所示。

非線性函數有4個輸入參數， 1個輸出參數， 設置神經網絡的結構為4-9-1。 輸入層有4個節點， 中間層有9個節點， 輸出層有1個節點， 共有4×9+9×1=45個權值， 9+1=10個閾值， 所以優化網絡的遺傳算法中， 實數編碼的染色體長度取55。 取函數的100組輸入輸出數據， 隨機取90組數據訓練網絡， 10組數據測試網絡性能， 將預測誤差的絕對值之和作為個體適應度， 適應度值越小， 個體越優。

將網絡優化遺傳算法尋得的最優初始權值和閾值賦值給神經網絡， 訓練之后預測函數的輸出， 再次用遺傳算法尋得擬合后函數的全局最大值。

尋優遺傳算法的最大迭代次數為200， 個體同樣采用實數編碼， 但個體長度對應尋優函數的輸入變量個數為4， 個體適應度值為神經網絡的預測值， 適應度值越大， 個體越優。

神經網絡的隱藏層激活函數選擇Logistic函數： f（x）=11+e-x， 輸出層的激活函數選擇修正線性單元函數（ReLU）： f（x）=max（0，x）。

5優化結果與分析

5.1神經網絡優化結果

遺傳算法優化神經網絡過程中的最優個體適應度值及平均適應度變化如圖11所示， 優化所得最優初始閾值、 權值見表1。

節點閾值-1.542 3將優化后的神經網絡參數值賦值并訓練后， 得到如圖12～13所示的預測誤差百分比及預測輸出。 可以看出， 神經網絡可以較準確地擬合非線性函數的輸出， 且預測誤差百分比在可接受的范圍內。

5.2航程極值尋優結果

用遺傳算法對優化后的神經網絡預測值進行極值尋優， 優化過程中的最優個體適應度值（最大航程）及平均適應度值變化曲線如圖14所示。

假設巡航飛行器始終保持最佳巡飛狀態， 由仿真結果可以看出， 飛行器在巡飛段的最大航程相比原來可以增加約18.03%， 對應的輸入參數為[33.121， 1.305， 0.0294， 0.0127]T， 即機翼面積約為1.305 m2， 機翼質量約33.121 kg時航程達到最大， 由已知模型可反推得， 飛行器翼展大約增加為原來1.16倍。 在某一確定翼展長度時， 升致阻力系數與零升阻力系數的值不會與質量、 面積的值精確對應， 因為阻力系數受具體飛行工況及其他因素的影響。 但該結果可以為飛行器的相關的優化設計提供參考。

6結論

本文對某巡航飛行器及其選定的飛行任務， 以翼展長度作為直接設計變量， 以飛行器的航程為目標， 采取遺傳算法與神經網絡擬合相結合的優化策略， 對機翼進行了優化設計。 優化結果表明： （1） 遺傳算法與神經網絡結合的方法可以兼顧優化精度與效率， 能夠對翼展進行快速優化， 從而得到飛行器航程最大時機翼的翼展長度與面積， 為巡航飛行器的航程優化設計提供參考。 （2） 本文在對航程進行優化時， 以具體工況氣動特性仿真結果為依據， 考慮其質量變化特性， 具有一定的創新性。 （3） 設計是在假設機翼結構強度滿足要求的前提下進行的， 在后續的研究中還需考慮具體的強度要求。 此外還可以對翼形、 展弦比、 后掠角等其他多種參數進行改進試驗、 優化仿真， 從而得到飛行性能更優的設計結果。

參考文獻：

[1] 高正紅， 王超. 飛行器氣動外形設計方法研究與進展[J]. 空氣動力學學報， 2017， 35（4）： 516-528.

Gao Zhenghong， Wang Chao. Aerodynamic Shape Design Methods for Aircraft： Status and Trends[J]. Acta Aerodynamic Sinica， 2017， 35（4）： 516-528.（in Chinese）

[2] Koreanschi A， Gabor O S， Acotto J， et al. Optimization and Design of an Aircrafts Morphing WingTip Demonstrator for Drag Reduction at Low Speeds[J]. Chinese Journal of Aeronautics， 2017， 30（1）：? 164-174.

[3] Mosbah A B， Botez R M， Dao M F. New Methodology for Calculating Flight Parameters with Neural NetworkEGD Method[C]∥ 60th Aeronautics Conference and AGM，? Toronto，? Canada， 2013： 19-22.

[4] Gabor O S， Koreanschi A， Botez R M. LowSpeed Aerodynamic Characteristics Improvement of ATR 42 Airfoil Using a Morphing Approach[C]∥ IECON 2012-38th Annual Conference on IEEE Industrial Electronics Society， 2012： 5451-6.

[5] Gabor O S， Simon A， Koreanschi A ，et al. Aerodynamic Performance Improvement of the UASS4 Ehecatl Morphing Airfoil Using Novel Optimization Techniques[J]. Proceedings of the Institution of Mechanical Engineers， Part G： Journal of Aerospace Engineering ， 2016， 230 （7）： 1164-1180.

[6] 王江華， 谷良賢， 龔春林. 伸縮彈翼巡航導彈氣動外形優化研究[J]. 飛行力學， 2009， 27（6）： 37-40.

Wang Jianghua， Gu Liangxian， Gong Chunlin. Shape Optimization of Cruise Missile Based on the Concept of Telescopic Wing[J]. Flight Dynamics， 2009， 27（6）： 37-40. （in Chinese）

[7] 張公平， 段朝陽， 廖志忠. 可變形翼戰術導彈氣動特性研究[J]. 飛行力學， 2011， 29（1）： 54-58.

Zhang Gongping， Duan Chaoyang， Liao Zhizhong. Study on Aerodynamic Characteristics of Tactical Missile with Morphing Wings [J]. Flight Dynamics， 2011， 29（1）：? 54-58. （in Chinese）

[8] 張登成， 羅浩， 張艷華， 等. 寬速域變構型高超聲速飛行器氣動特性研究[J]. 固體火箭技術， 2019， 42（1）： 128-134.

Zhang Dengcheng， Luo Hao， Zhang Yanhua， et al. Aerodynamic Analysis of a WideRanged Morphing Hypersonic Vehicle[J]. Journal of Solid Rocket Technology， 2019， 42（1）： 128-134. （in Chinese）

[9] 馬洋， 周偉， 秦偉偉. 基于升力體的變構型超聲速飛行器氣動特性研究[C] ∥首屆兵器工程大會論文集， 重慶， 2017： 799-802.

Ma Yang， Zhou Wei， Qin Weiwei. Aerodynamic Characteristics of Variable Configuration Supersonic Aircraft Based on Lift Body[C] ∥ Proceedings of the First Ordnance Engineering Conference， Chongqing， 2017： 799-802.（in Chinese）

[10] Klimczyk W A， Goraj Z. Analysis and Optimization of Morphing Wing Aerodynamics[J]. Aircraft Engineering and Aerospace Technology， 2018， 91（3）： 538-546.

[11] 徐國武， 白鵬， 陳冰雁. 可變形飛行器新概念升阻特性分析[J].力學季刊， 2013， 34（3）： 444-450.

Xu Guowu， Bai Peng， Chen Bingyan. Analysis on the LiftDrag Characteristics of New Concept Morphing Aircraft[J]. Chinese Quarterly of Mechanics， 2013，34（3）： 444- 450. （in Chinese）

[12] 馬超， 吳大衛， 俞金海， 等. 基于參數化模型的大型民用飛機設計航程研究[J]. 航空學報， 2016， 37（1）：? 112-121.

Ma Chao， Wu Dawei， Yu Jinhai， et al. Design Range Research of Large Civil Aircraft Based on Parametric Model[J]. Acta Aeronautica et Astronautica Sinica， 2016， 37（1）： 112-121. （in Chinese）