基于聯(lián)合特征參數(shù)提取的非合作信號(hào)調(diào)制識(shí)別算法

司海飛，胡興柳，史震，李仕勇

（1.金陵科技學(xué)院智能科學(xué)與控制工程學(xué)院，江蘇 南京 211169；2.哈爾濱工程大學(xué)自動(dòng)化學(xué)院，黑龍江 哈爾濱 150001；3.哈爾濱工程大學(xué)信息與通信工程學(xué)院，黑龍江 哈爾濱 150001）

1 引言

在合作通信中，通信雙方依據(jù)事先既定傳輸協(xié)議進(jìn)行通信；而非合作通信中，通信傳輸信息的數(shù)據(jù)調(diào)制方式以及信號(hào)的編碼方式等參數(shù)對(duì)接收端是未知的，需要先對(duì)信號(hào)進(jìn)行各種合理的參數(shù)估計(jì)，再對(duì)信號(hào)進(jìn)行下一步分析。

當(dāng)前雷達(dá)系統(tǒng)和通信系統(tǒng)的自適應(yīng)程度越來(lái)越高，所采用的波形越來(lái)越先進(jìn)，調(diào)制方式也越來(lái)越復(fù)雜。同時(shí)，用頻設(shè)備數(shù)量飛速增加，頻譜變得越來(lái)越擁塞。解決調(diào)制方式復(fù)雜，用頻設(shè)備增多，頻譜擁塞且電磁環(huán)境干擾增加等因素給非合作信號(hào)識(shí)別處理帶來(lái)的問(wèn)題有著重要意義。

目前，國(guó)內(nèi)外研究主要針對(duì)單載波、正交頻分復(fù)用（OFDM,orthogonal frequency division multiplexing）信號(hào)的識(shí)別，對(duì)OFDM 波形傳輸子載波間的調(diào)制識(shí)別研究文獻(xiàn)較少。Karra 等[1]認(rèn)為可以采用能量檢測(cè)的方法來(lái)對(duì)OFDM 進(jìn)行檢測(cè)。其思路是利用在高斯白噪聲信道中信號(hào)噪聲能量之和大于單獨(dú)的白噪聲能量，設(shè)置合適的門(mén)限閾值將信號(hào)從這種復(fù)雜的環(huán)境中檢測(cè)出來(lái)。但在實(shí)際通信環(huán)境中，要選擇合適的門(mén)限閾值是極其困難的，尤其是在復(fù)雜的微弱電磁環(huán)境中，噪聲能量遠(yuǎn)大于信號(hào)的能量，或噪聲為非平穩(wěn)時(shí)，信號(hào)檢測(cè)結(jié)果會(huì)急劇惡化。

Dillard[2]認(rèn)為雷達(dá)中的脈沖檢測(cè)、二元滑窗技術(shù)與能量檢測(cè)算法可以結(jié)合起來(lái)做信號(hào)檢測(cè)，但沒(méi)有從根本上解決能量檢測(cè)門(mén)限閾值難以選取的問(wèn)題。基于此，Krasner[3]提出了結(jié)合經(jīng)典檢測(cè)和估計(jì)理論的算法，傳輸數(shù)據(jù)的各種信息都是已知的，先存儲(chǔ)在接收端的處理器中。

隨著通信技術(shù)飛速發(fā)展，OFDM 信號(hào)盲檢測(cè)越來(lái)越受到人們的關(guān)注，Shi 等[4]對(duì)OFDM 與直接序列擴(kuò)頻（DS-SS,direct sequence spread spectrum）信號(hào)都具有的譜線間隱含周期性特征進(jìn)行研究，把功率譜二次處理以及倒譜分析方法作為OFDM 檢測(cè)識(shí)別的算法，使OFDM 信號(hào)能夠在信噪比（SNR,signal to noise ratio）非常低的情況下實(shí)現(xiàn)盲檢測(cè)和參數(shù)的盲估計(jì)。

在實(shí)際通信中，常見(jiàn)信號(hào)都是循環(huán)平穩(wěn)的，因此建立循環(huán)平穩(wěn)的信號(hào)模型可以滿足通常情況下的算法仿真。Jaiswal 等[5]提出一種利用譜相關(guān)對(duì)信號(hào)的調(diào)制方式進(jìn)行分析的方法，得到不同調(diào)制方式信號(hào)各自的周期特征。在已有研究中，信號(hào)的循環(huán)平穩(wěn)性經(jīng)常被用來(lái)進(jìn)行信號(hào)的檢測(cè)、參數(shù)估計(jì)、調(diào)制方式識(shí)別、信道估計(jì)等盲研究[6]，基于此的OFDM 信號(hào)盲處理[7]技術(shù)也在不斷進(jìn)步。

從信號(hào)類別上，調(diào)制識(shí)別分為類間識(shí)別和類內(nèi)識(shí)別2 種，類間識(shí)別包括多進(jìn)制數(shù)字相位調(diào)制（MPSK,multiple phase shift keying）和多進(jìn)制正交幅度調(diào)制（MQAM,multiple quadrature amplitude modulation）等，類內(nèi)識(shí)別包括16QAM 和64QAM等[8]。在目前的研究中，從識(shí)別算法上，調(diào)制識(shí)別分為兩大類，即決策論識(shí)別和模式識(shí)別。決策論識(shí)別通常用于在待識(shí)別信號(hào)中至少能識(shí)別出一種的情形，其思想是根據(jù)信號(hào)能否滿足假設(shè)的條件來(lái)進(jìn)行識(shí)別；模式識(shí)別是根據(jù)統(tǒng)計(jì)信息提取特征量進(jìn)行識(shí)別。本文采用模式識(shí)別中的基于高階統(tǒng)計(jì)量算法來(lái)完成調(diào)制識(shí)別。

依據(jù)不同的調(diào)制方式，可以得到多種信號(hào)參數(shù)，因此研究者提出了各種特征量的構(gòu)造方式，例如，信號(hào)瞬時(shí)參數(shù)和功率譜特征[9]、信號(hào)高階統(tǒng)計(jì)量[10]、小波變換方法[11]、分形理論算法、信號(hào)星座圖法等。

本文以非合作OFDM 調(diào)制信號(hào)發(fā)送接收為背景，對(duì)信號(hào)的盲檢測(cè)、參數(shù)盲估計(jì)、子載波調(diào)制識(shí)別進(jìn)行研究分析。

2 OFDM 信號(hào)模型

2.1 OFDM 系統(tǒng)理論

由文獻(xiàn)[12-14]可知，OFDM 是一種特殊的多載波調(diào)制技術(shù)。OFDM 基本思想是，將信道分成若干正交子信道，將串行的高速數(shù)據(jù)流信號(hào)轉(zhuǎn)換成并行的低速子數(shù)據(jù)流，并調(diào)制到每個(gè)子信道上進(jìn)行傳輸。OFDM 系統(tǒng)框架如圖1 所示，在OFDM 通信系統(tǒng)中，每個(gè)OFDM 符號(hào)由調(diào)制后的子載波進(jìn)行相加而成，每個(gè)子載波都可以根據(jù)實(shí)際情況選擇合適的調(diào)制方式，如MPSK 或MQAM。

其中，t為時(shí)間，ts為起始時(shí)間，N為子信道的數(shù)目；Tc為OFDM 符號(hào)的持續(xù)時(shí)間長(zhǎng)度；di為第i個(gè)子載波上傳輸?shù)臄?shù)據(jù)符號(hào)；fi為第i個(gè)子載波使用的頻率點(diǎn)，fc為載頻；rect(t)為矩形函數(shù)，rect(t)=1，；s(t)=0，t＜ts或t＞Tc+ts。

圖1 OFDM 系統(tǒng)框架

各子載波相互正交，即

對(duì)第i個(gè)子信道上傳輸?shù)臄?shù)據(jù)進(jìn)行解調(diào)，在數(shù)據(jù)持續(xù)時(shí)間Tc內(nèi)積分，即

各子信道頻率點(diǎn)間有若干整數(shù)倍周期差，因此其他子載波此時(shí)的積分值為零。由式(3)可知，如果對(duì)接收信號(hào)中的任一子載波信號(hào)進(jìn)行解調(diào)，就能恢復(fù)原子載波信號(hào)。

在OFDM 系統(tǒng)中，由數(shù)據(jù)持續(xù)時(shí)間長(zhǎng)度Tc可得子信道的帶寬為進(jìn)而可知一個(gè)OFDM 符號(hào)的帶寬為

另外，從頻域角度來(lái)對(duì)OFDM 子載波間的位置進(jìn)行分析，在符號(hào)持續(xù)時(shí)間之內(nèi)，包括了許多子載波，因此它的頻譜可以認(rèn)為是矩形脈沖與許多位于子載波頻率點(diǎn)上的δ函數(shù)在頻域的卷積相加。已知矩形脈沖頻譜函數(shù)為sinc(Tc f)，該函數(shù)在OFDM 周期倒數(shù)的整數(shù)倍處均為零。由此可知，在每一個(gè)子頻率點(diǎn)上都有一個(gè)最大值，而對(duì)應(yīng)的時(shí)刻，其他子信道上的頻譜值等于零，即消除了碼間干擾（ICI,inter-chip interference）。

令s(t)中的ts=0，此時(shí)矩形函數(shù)可當(dāng)作不存在，對(duì)s(t)以的速率進(jìn)行采樣，即令，可得

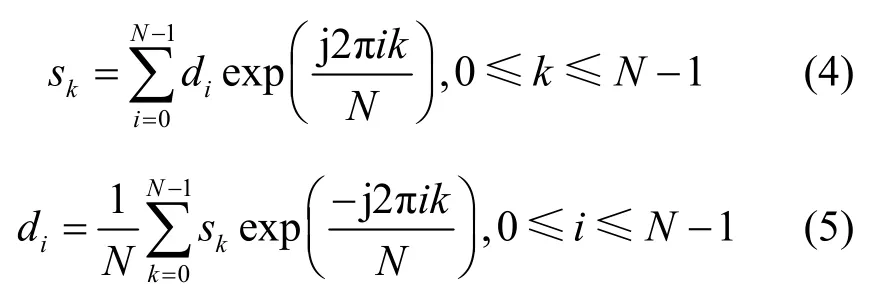
由此可知，離散傅里葉逆變換（IDFT,inverse discrete Fourier transform）和離散傅里葉變換（DFT,discrete Fourier transform）可用來(lái)完全代替OFDM的調(diào)制解調(diào)技術(shù)，IDFT 運(yùn)算之后，頻域符號(hào)d就被轉(zhuǎn)換成時(shí)域符號(hào)s，再將s解調(diào)恢復(fù)成d就取得了原始數(shù)據(jù)。另外可通過(guò)快速傅里葉逆變換（IFFT,inverse fast Fourier transform）和快速傅里葉變換（FFT,fast Fourier transform）代替IDFT 和DFT，進(jìn)一步降低運(yùn)算量。

2.2 信道編碼

信號(hào)在經(jīng)過(guò)信道傳輸時(shí)會(huì)受到噪聲的干擾，使接收數(shù)據(jù)存在較大的誤差，信道編碼和解碼在傳輸?shù)男畔⒅刑砑雍腿コ哂喽龋ＷC信息傳輸?shù)臏?zhǔn)確性[15-16]。本文選擇卷積碼，輸入位有k個(gè)，輸出位有n個(gè)，具有m節(jié)移位寄存器，構(gòu)成的有限狀態(tài)的有記憶系統(tǒng)原理如圖2 所示。

圖2 卷積碼編碼器原理

將輸入信息序列u接到系統(tǒng)中，再進(jìn)行相應(yīng)邏輯計(jì)算，就可以得到輸出碼字序列c。

1967 年Viterbi 提出了Viterbi 譯碼算法，1969年Omura 證明了Viterbi 譯碼算法是最大似然譯碼算法，其特別之處是利用了卷積碼的網(wǎng)絡(luò)結(jié)構(gòu)，從而在很大程度上降低了譯碼的復(fù)雜度。

2.3 擴(kuò)頻與解擴(kuò)

將偽噪聲序列和需要傳輸?shù)幕鶐?shù)據(jù)進(jìn)行相乘運(yùn)算，這種方式稱為直擴(kuò)，擴(kuò)頻需要的調(diào)制序列由專門(mén)的偽噪聲產(chǎn)生器得到。DS-SS 通信發(fā)射框架如圖3 所示。

圖3 DS-SS 通信發(fā)射框架

用戶收到的擴(kuò)頻信號(hào)如式(6)所示。

其中，m(t)表示傳輸?shù)男盘?hào)，p(t)是偽隨機(jī)序列（PN,pseudo-noise）碼。由此得到的信號(hào)波形滿足時(shí)間上的無(wú)重疊情況，且為矩形脈沖，幅度為±1。m(t)符號(hào)周期為T(mén)s，p(t)中矩形脈沖周期為T(mén)c，Ts和Tc相差整數(shù)倍。

2.4 保護(hù)間隔

實(shí)際通信中，數(shù)據(jù)傳輸?shù)男诺蓝际嵌鄰叫诺溃鄰綍?huì)在時(shí)域造成時(shí)延拓展，通信的脈沖響應(yīng)會(huì)產(chǎn)生嚴(yán)重的拖尾情況，進(jìn)而出現(xiàn)符號(hào)間干擾；多徑信道還會(huì)在頻域造成頻率選擇性衰落，從而影響正交性，對(duì)OFDM 系統(tǒng)的影響十分嚴(yán)重。為了消除或減小符號(hào)間干擾、頻率選擇性衰落的影響，需要加入保護(hù)間隔[17]。保護(hù)間隔長(zhǎng)度超過(guò)多徑問(wèn)題帶來(lái)的時(shí)延拓展時(shí)可以忽略掉由于OFDM 符號(hào)帶來(lái)的影響[18]。保護(hù)間隔Tg提高通信系統(tǒng)性能的同時(shí)會(huì)帶來(lái)功率損耗升高，可通過(guò)式(7)定量分析。

2.5 基于IFFT 技術(shù)的OFDM 信號(hào)

用IFFT 和FFT 技術(shù)來(lái)實(shí)現(xiàn)OFDM 調(diào)制解調(diào)需要保證子載波間嚴(yán)格正交，系統(tǒng)框架如圖4 所示，其中LPF 為低通濾波器。2 個(gè)正交子載波sin(t)、sin(2t)能夠推廣到一個(gè)正交信號(hào)集合，稱為正交基。根據(jù)歐拉公式，ejwnt就是OFDM 信號(hào)的正交基[6]。

以T為采樣間隔對(duì)信號(hào)SOFDM(t)采樣，基帶OFDM 信號(hào)的采樣表達(dá)式為

其中，ωn=ωc+nΔω，ωn為第n個(gè)子載波角頻率，ωc為載波角頻率，dn(t)為第n個(gè)子載波上的復(fù)信號(hào)，如果在符號(hào)周期Tc內(nèi)采樣N個(gè)點(diǎn)，則Tc=NTa。

基帶OFDM 信號(hào)上變頻形成發(fā)射信號(hào)。所以基帶處理時(shí)ωc=0，則式(8)可以簡(jiǎn)化為

而離散傅里葉反變換為

從式(9)和式(10)可知，如果dn(t)是頻域的采樣，則SOFDM(kTa)為相應(yīng)的時(shí)域波形，若則式(9)與式(10)等效，可得到子載波使用頻率點(diǎn)的間隔

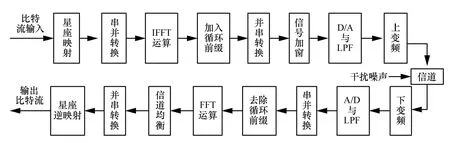
圖4 基于FFT/IFFT 的OFDM 調(diào)制通信系統(tǒng)框架

2.6 OFDM 信號(hào)模型仿真

2.6.1 OFDM 正交性驗(yàn)證

OFDM 通信傳輸系統(tǒng)中，各子頻率點(diǎn)保持著正交關(guān)系。通過(guò)MATLAB 仿真檢驗(yàn)其正交性，仿真結(jié)果如圖5 所示。

圖5 OFDM 子載波正交性仿真

OFDM 符號(hào)周期內(nèi)有許多子載波，從頻域的角度對(duì)OFDM 子載波間的位置進(jìn)行分析，在符號(hào)持續(xù)時(shí)間之內(nèi)，子載波的頻譜可以認(rèn)為是矩形脈沖與位于子載波頻率點(diǎn)上的函數(shù)在頻域的卷積相加。如圖5所示，OFDM 包含5 個(gè)子頻率點(diǎn)。圖5 中每個(gè)子頻率點(diǎn)上都有一個(gè)最大值，而此時(shí)，其他子頻率點(diǎn)上頻譜值為零，驗(yàn)證了仿真模型滿足正交性要求。

2.6.2 OFDM 信號(hào)時(shí)域特性

圖6 為基帶數(shù)據(jù)經(jīng)過(guò)星座映射后的星座圖。QPSK 對(duì)應(yīng)于星座圖上的4 個(gè)點(diǎn)，16QAM 信號(hào)映射為星座圖上16 個(gè)點(diǎn)，為了使OFDM 通信傳輸過(guò)程信號(hào)的功率分布均勻，需要對(duì)星座映射后的碼元信號(hào)進(jìn)行歸一化處理。

圖6 基帶數(shù)據(jù)星座圖

OFDM 信號(hào)在時(shí)域上是若干子載波的調(diào)制信號(hào)疊加之和，圖7 為多個(gè)子載波組成的OFDM 符號(hào)時(shí)域圖。在仿真中，需要先假設(shè)所有子載波的幅值相位相同。但是在實(shí)際的通信傳輸中，每個(gè)子載波的參數(shù)都是不確定的，都由各自的信道以及傳輸?shù)臄?shù)據(jù)選擇不同的調(diào)制方式，也就導(dǎo)致各自的幅值相位都不相同。

圖7 多個(gè)子載波組成的OFDM 符號(hào)時(shí)域圖

由圖7 可以看出，在同一時(shí)刻，存在不同的頻率的波形進(jìn)行傳輸。當(dāng)子載波個(gè)數(shù)較多時(shí)，在時(shí)域上很難對(duì)每個(gè)子載波信號(hào)進(jìn)行區(qū)分。

本文模型中子載波采用的調(diào)制信號(hào)有空子載波、QPSK、16QAM，其中OFDM 子載波數(shù)目確定為64，因此循環(huán)前綴（CP,cyclic prefix）的符號(hào)長(zhǎng)度為16，傳輸數(shù)據(jù)的子載波數(shù)為53，導(dǎo)頻數(shù)量為11。碼元速率為20 Mbaud/s；設(shè)定單載波信號(hào)速率為4 Mbit/s。

OFDM 信號(hào)時(shí)域波形仿真如圖8 所示。

圖8 OFDM 信號(hào)時(shí)域波形仿真

由于很多信號(hào)進(jìn)行疊加，在時(shí)域上分布密集。如果對(duì)時(shí)域信號(hào)進(jìn)行加窗處理，則得到的時(shí)域波形會(huì)較為平滑。OFDM 波形的功率譜帶外衰減速度不快，而加窗技術(shù)可以使OFDM 波形處于帶外的部分衰減速度加快，此時(shí)每一個(gè)OFDM 信號(hào)在其周期的邊緣幅值就能實(shí)現(xiàn)逐漸平滑地過(guò)渡到零。其經(jīng)過(guò)加窗處理后的時(shí)域波形如圖9 所示。

圖9 OFDM 信號(hào)加窗后的時(shí)域波形

數(shù)據(jù)進(jìn)行相應(yīng)的處理后進(jìn)行傳輸，在接收端接收到的數(shù)據(jù)解調(diào)星座圖如圖10 和圖11 所示。

圖10 QPSK 信號(hào)OFDM 調(diào)制解調(diào)后的星座圖

從解調(diào)星座圖可以看出，在接收端解調(diào)處理后的信號(hào)與原始數(shù)據(jù)相比，受到了信道的影響，星座點(diǎn)在一定的范圍內(nèi)變化，但始終能夠設(shè)置合適的閾值對(duì)信號(hào)進(jìn)行正確解調(diào)輸出。

2.6.3 OFDM 信號(hào)頻域特性

由仿真參數(shù)可知導(dǎo)頻數(shù)量為11，導(dǎo)頻可以用于接收端的接收處理，圖12 展示了OFDM 信號(hào)的頻譜圖，圖12 中峰值表示導(dǎo)頻。

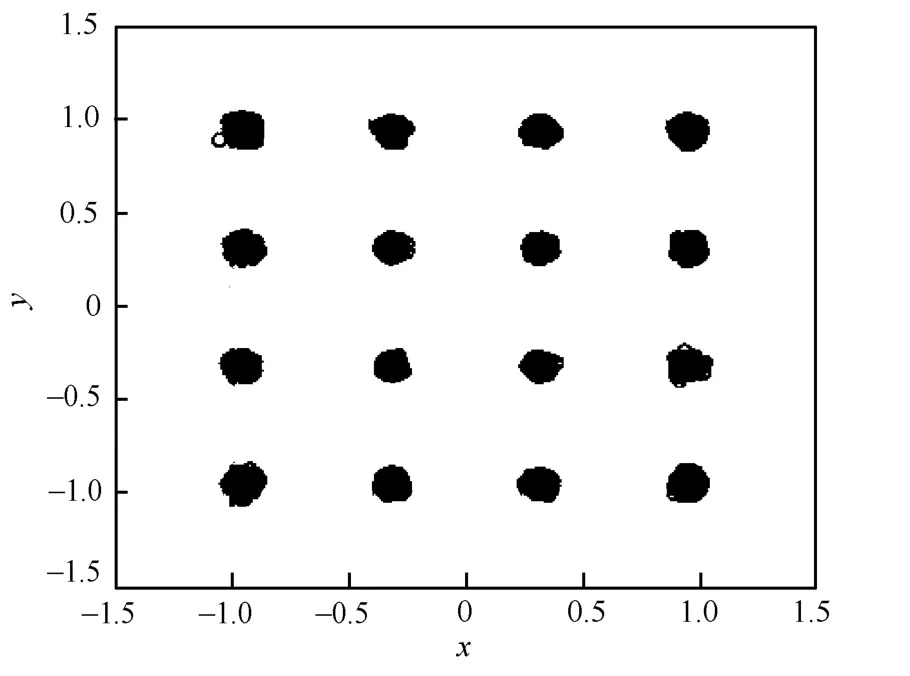
圖11 16QAM 信號(hào)OFDM 調(diào)制解調(diào)后的星座圖

圖12 OFDM 信號(hào)的頻譜圖

2.6.4 OFDM 信號(hào)誤比特率曲線仿真

本文的OFDM 信號(hào)仿真模型誤比特率如圖13 所示。當(dāng)信噪比達(dá)到9 dB 時(shí)，輸入的解調(diào)數(shù)據(jù)能夠達(dá)到10-6以下。證明本文基于IFFT 運(yùn)算的子載波包含不同調(diào)制方式的OFDM 信號(hào)仿真模型搭建成功，滿足研究需求，下面對(duì)OFDM 信號(hào)展開(kāi)相應(yīng)的研究分析。

圖13 OFDM 信號(hào)仿真模型誤比特率

3 OFDM 信號(hào)的存在性檢測(cè)算法

3.1 高階累積量

對(duì)于一組隨機(jī)變量[s1,s2,…,sn]，如果它們是平穩(wěn)的且取實(shí)數(shù)，則它們的聯(lián)合r=k1+k2+…+kn階累積量定義為

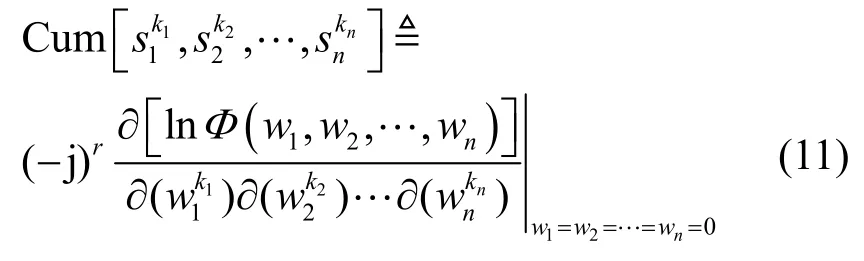
高階統(tǒng)計(jì)量的性質(zhì)如下。

1) 若λi（i=1,…,k）為常數(shù)，且xi（i=1,…,k）為隨機(jī)變量，則有

2) 對(duì)于變量的取值累積量的值有著對(duì)稱性，即

其中，(l1,…,lk)為(1,…,k)的任意一個(gè)排列。

3) 若隨機(jī)變量{xl}與隨機(jī)變量{yl}獨(dú)立，則有

3.2 基于高階累積量的OFDM 信號(hào)檢測(cè)

OFDM 信號(hào)在時(shí)域上是若干子載波的調(diào)制信號(hào)疊加之和，考慮中心極限定理的情況，由此可知OFDM信號(hào)呈漸進(jìn)正態(tài)分布。隨著子載波數(shù)量增加，信號(hào)逼近正態(tài)性。但單載波調(diào)制信號(hào)是非高斯性的，因此選取構(gòu)造一種4 階累積量作為信號(hào)識(shí)別的特征參數(shù)[19-20]，可以把OFDM 信號(hào)從待識(shí)別信號(hào)集合中識(shí)別出來(lái)。

在此基礎(chǔ)上，考慮到目前電磁環(huán)境的復(fù)雜情況，本文構(gòu)造一種新的聯(lián)合特征參數(shù)進(jìn)行OFDM 信號(hào)檢測(cè)。在瑞利信道環(huán)境下進(jìn)行研究，信道高斯時(shí)信道是被視作理想的。即H0：s(t)是OFDM 信號(hào)；H1：s(t)是單載波調(diào)制信號(hào)。

1) 單載波信號(hào)

其中，fc為載頻，θc為載波初始相位，為基帶傳輸數(shù)據(jù)。

理想高斯信道條件下的接收信號(hào)y(t)模型為

其中，s(t)是所有可能接收到的數(shù)字調(diào)制信號(hào)，w(t)是復(fù)加性高斯白噪聲。

對(duì)于PSK 信號(hào)，有

2) OFDM 信號(hào)的漸進(jìn)高斯性

功率歸一化后的OFDM 信號(hào)s(t)模型為

其中，cn,k為發(fā)射機(jī)產(chǎn)生的符合假設(shè)分布的符號(hào)數(shù)據(jù)；fc為載頻；Δf為子載波頻率點(diǎn)間隔，通常情況下；g(t)為成型函數(shù)；Tc為OFDM 波形有效數(shù)據(jù)持續(xù)時(shí)間，Ts=Tc+Tg代表了包含保護(hù)間隔的OFDM 符號(hào)持續(xù)時(shí)間，Tg是CP 長(zhǎng)度。

把復(fù)OFDM 信號(hào)s(t)分為實(shí)部sr(t)和虛部si(t)，如式(28)所示。

由各子載波數(shù)據(jù)間的獨(dú)立性和累積量線性性質(zhì)，可以得到t=t0時(shí)信號(hào)實(shí)部sr(t)的4 階累積量為

隨著N的增大，可得Cum4(sr)趨近于0。

對(duì)于信號(hào)虛部si(t)的計(jì)算也可以得到一樣的值。可知OFDM 信號(hào)具有漸近正態(tài)分布特性，其4階累積量取值為零。而單載波調(diào)制信號(hào)并不服從漸進(jìn)正態(tài)分布，由此得到的4 階累積量是不等于零的。該特征參數(shù)下，高斯白噪聲的取值為零，可以忽略噪聲的影響。因此，根據(jù)待檢測(cè)信號(hào)的4 階累積量可對(duì)單載波調(diào)制信號(hào)和OFDM 信號(hào)加以區(qū)分，從而檢測(cè)出OFDM 信號(hào)。

多徑信道中也可采用一種在4 階統(tǒng)計(jì)量的基礎(chǔ)上進(jìn)行特征參數(shù)改進(jìn)的方法對(duì)OFDM 實(shí)現(xiàn)波形檢測(cè)[21]。

多徑慢衰落信道環(huán)境下接收信號(hào)r(n)模型如式(31)所示。

其中，s(n)為所有可能接收到的數(shù)字調(diào)制信號(hào)；h(n)為不同的路徑增益，慢衰落信道中，h(n)被視作一個(gè)常數(shù)hl(n)=hl；τl為不同路徑時(shí)延；L為多徑數(shù)目；w(n)為加性高斯白噪聲。已有的算法通過(guò)提取特征量C40進(jìn)行檢測(cè)。本文采用接收信號(hào)r(n)的作為檢測(cè)特征量，如式(32)所示。

多徑數(shù)目L是一個(gè)有限的值，而且所有子信道的增益hl是一個(gè)確定的且有限大的值。對(duì)于OFDM信號(hào)有

結(jié)合式(32)和式(33)可得

由前文的推導(dǎo)可知，對(duì)于接收機(jī)收到的單載波調(diào)制信號(hào)，其沒(méi)有表現(xiàn)出正態(tài)分布特性，所以它們的是非零的。

如果直接使用特征量C40作為檢測(cè)參數(shù)，還需要考慮頻偏的影響[22]。本文研究中采用聯(lián)合特征量方式，即構(gòu)造C42和C21的組合，這樣排除載波頻率以及在傳輸過(guò)程中造成的頻偏對(duì)參數(shù)的影響，能夠?qū)χ蓄l信號(hào)進(jìn)行直接處理，而不需要中頻信號(hào)下變頻到基帶。

4 參數(shù)盲估計(jì)與子載波調(diào)制識(shí)別

4.1 OFDM 信號(hào)參數(shù)盲估計(jì)

由Ts=Tc+Tg知，對(duì)整個(gè)OFDM 符號(hào)長(zhǎng)度和保護(hù)間隔長(zhǎng)度進(jìn)行估計(jì)，可得有效數(shù)據(jù)的持續(xù)時(shí)間長(zhǎng)度。

OFDM 的時(shí)域符號(hào)結(jié)構(gòu)如圖14 所示。由圖14可知，只需計(jì)算OFDM 符號(hào)的數(shù)據(jù)間相關(guān)值，找到相關(guān)函數(shù)的峰值就能得到數(shù)據(jù)的符號(hào)長(zhǎng)度，對(duì)OFDM 的符號(hào)數(shù)估計(jì)直接關(guān)系到對(duì)其子載波調(diào)制方式識(shí)別的準(zhǔn)確性。

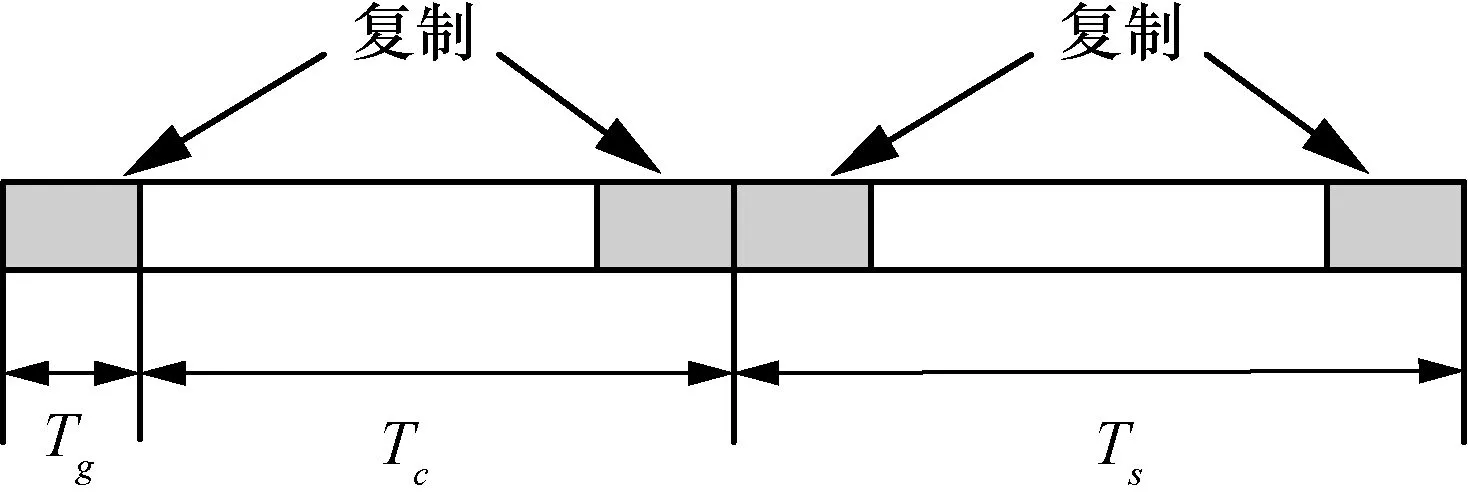
圖14 OFDM 的時(shí)域符號(hào)結(jié)構(gòu)

計(jì)算接收數(shù)據(jù)r(n)=s(n)+w(n)的自相關(guān)時(shí)，如果CP 和它的復(fù)制源進(jìn)行相關(guān)運(yùn)算，可得峰值為

可采用一種控制偏移長(zhǎng)度的方法計(jì)算數(shù)據(jù)流的相關(guān)性，以達(dá)到對(duì)有效符號(hào)長(zhǎng)度進(jìn)行估計(jì)。在偏移長(zhǎng)度的改變中，相關(guān)函數(shù)出現(xiàn)峰值的坐標(biāo)就是有效符號(hào)長(zhǎng)度N。在計(jì)算過(guò)程中，把數(shù)據(jù)的能量進(jìn)行歸一化處理就能消除計(jì)算抖動(dòng)。計(jì)算數(shù)據(jù)的有效符號(hào)長(zhǎng)度的方法如下。

其中，M為計(jì)算中所用符號(hào)長(zhǎng)度，L為在計(jì)算開(kāi)始時(shí)對(duì)有效符號(hào)長(zhǎng)度的估計(jì)，k為受控制變化的偏移長(zhǎng)度，r(i)為第i個(gè)數(shù)據(jù)，峰值坐標(biāo)即為有效符號(hào)長(zhǎng)度，Ru(k)為相關(guān)偏移長(zhǎng)度為1～L的相關(guān)結(jié)果，Enu(k)為該段數(shù)據(jù)的能量。

圖15 確定窗口長(zhǎng)度估計(jì)符號(hào)長(zhǎng)度

其中，m為偏移窗口初始位置，j為數(shù)據(jù)在可變窗口中的位置，r(j)為對(duì)應(yīng)的數(shù)據(jù)，L’為窗口大小，Rl(m)為在整個(gè)窗口中的所有相關(guān)值之和，Enl(m)為此窗口之內(nèi)的信號(hào)能量，LEN(m)是為了消除抖動(dòng)采用的歸一化處理值。因此在計(jì)算過(guò)程中，只需要找到LEN(m)的2 個(gè)峰值，再確定2 個(gè)峰值之間的距離就能知道整個(gè)OFDM 符號(hào)的符號(hào)長(zhǎng)度NOFDM。

已知OFDM 的符號(hào)長(zhǎng)度NOFDM和有效符號(hào)長(zhǎng)度?N，可求得CP 長(zhǎng)度。至此，關(guān)于OFDM 的符號(hào)參數(shù)已全部獲取。

Enu(k)和Enl(m)都是信號(hào)的能量，環(huán)境所帶來(lái)的相偏和頻偏不會(huì)對(duì)其造成影響。在式(37)和式(40)中使用了共軛乘法運(yùn)算，因此相偏對(duì)Ru(k)和Rl(m)也沒(méi)有影響。若存在頻偏，Ru(k)和Rl(m)中會(huì)出現(xiàn)一個(gè)復(fù)數(shù)因子，但|Ru(k)|對(duì)該復(fù)數(shù)因子也不敏感，因此相移和頻移在此方法中都可避免。

4.2 基于聯(lián)合特征參數(shù)Gr 方法的子載波調(diào)制識(shí)別

在實(shí)際的長(zhǎng)期演進(jìn)（LTE,long term evolution）通信中，對(duì)于通信系統(tǒng)的下行數(shù)據(jù)，OFDM信號(hào)的子載波上可以采用多種調(diào)制方式，對(duì)其準(zhǔn)確識(shí)別是研究的主要任務(wù)。在獲取到了OFDM 的符號(hào)參數(shù)，并且已經(jīng)進(jìn)行了準(zhǔn)確的同步之后，本文采用一種聯(lián)合特征參數(shù)的方法來(lái)對(duì)子載波進(jìn)行調(diào)制識(shí)別。

1) 本文研究的子載波數(shù)據(jù)映射方式有{空子載波,QPSK,16QAM}，各個(gè)子載波上的調(diào)制方式是M種中的一種，即

其中，d(i,n)為第i個(gè)OFDM 中第n個(gè)子信道的調(diào)制方式，均值是0，方差是1，且各個(gè)信號(hào)等概率出現(xiàn)，即

2) 接收機(jī)得到的離散采樣序列已實(shí)現(xiàn)準(zhǔn)確的同步。

3) 信道變換不明顯；多徑信道的每條信道噪聲是均值為零、方差為σ2的復(fù)白噪聲。實(shí)際中，多徑衰落信道通常用FIR 模型來(lái)表示，如式(44)所示。

其中，L為濾波的階數(shù)，al(l=0,1,…,L–1)為各階濾波的程度。此時(shí)多徑信道模型如圖16 所示。

圖16 等效并行衰落信道

其中，H(k)為信道h(k)的信道響應(yīng)，Td為抽樣周期。每個(gè)信道的數(shù)學(xué)表達(dá)式為

其中，R(i,n)為第i個(gè)接收數(shù)據(jù)的第n個(gè)子載波上的數(shù)據(jù)，W(i,n)為零均值的復(fù)正態(tài)分布過(guò)程，H(i,n)為信道傳遞函數(shù)。

對(duì)于上述OFDM通信信道模型中的第n個(gè)子信道數(shù)據(jù)，可表示為

其中，k=1,2,…,N，n=0,1,…,N-1，dn(k)為第n個(gè)子信道上傳輸?shù)臄?shù)據(jù)，Es為數(shù)據(jù)的功率密度，h(n)、θ(n)分別為第n條子載波上幅度相位相應(yīng)的變化，wn(k)為白噪聲。

選取的特征量定義為

對(duì)于OFDM 調(diào)制方式下的各子信道傳輸數(shù)據(jù)序列dn(k)。表1 為各種映射方式的C20的參考值。

表1 功率歸一化后C20 參考值

從表1 可知，選取的特征參數(shù)能夠用來(lái)檢測(cè)空子載波，并可將子信道上映射方式分成3 類，即{空子載波}{MPSK }和{MQAM}。

特征參數(shù)構(gòu)造的過(guò)程中消除掉了信道的影響，因此，特征參數(shù)C20和Gr對(duì)子信道的常見(jiàn)消極影響都不敏感。C20將傳輸數(shù)據(jù)分為3 類，即{空子載波}{MPSK}和{MQAM}，然后用Gr區(qū)分QPSK 與16QAM 信號(hào)。Gr的參考值如表2 所示。

表2 功率歸一化后Gr 參考值

設(shè)定相應(yīng)的閾值，并采用式(50)所示的判決準(zhǔn)可將OFDM 子載波上的調(diào)制方式進(jìn)行識(shí)別分類。

其中，i取值分別對(duì)應(yīng)調(diào)制集合中的調(diào)制方式{空子載波}{QPSK}和{16QAM}，為計(jì)算得到的接收序列的特征值，為調(diào)制方式為Mi時(shí)對(duì)應(yīng)信號(hào)識(shí)別特征參數(shù)的理論值，為識(shí)別出的子載波調(diào)制方式。

5 仿真實(shí)驗(yàn)

5.1 OFDM 信號(hào)檢測(cè)

本實(shí)驗(yàn)仿真中采用的調(diào)制信號(hào)有 QPSK、16QAM、64QAM、OFDM。OFDM 子載波個(gè)數(shù)64，有效子載波數(shù)52，碼元速率為20 Mbaud/s；單載波信號(hào)比特速率為4 Mbit/s。仿真信道信噪比為-10～25 dB。關(guān)于檢測(cè)OFDM 的聯(lián)合特征參數(shù)的理論推導(dǎo)值，如表3 所示。由表3 可知，設(shè)置合理的閾值門(mén)限就可以將OFDM 信號(hào)與其他單載波信號(hào)區(qū)分開(kāi)。仿真結(jié)果如圖17 所示。

表3 各種單載波信號(hào)的理論值

表3 各種單載波信號(hào)的理論值

仿真信噪比條件為-10～25 dB。由圖17 可看出，在信噪比大于-2 dB 時(shí)，可設(shè)定閾值從QPSK、16QAM、64QAM 中檢測(cè)出OFDM 信號(hào)。

對(duì)其進(jìn)行蒙特卡洛仿真，每個(gè)信噪比下仿真100 次得到OFDM 波形的檢測(cè)準(zhǔn)確率，從圖17 可以看出，在信噪比較低時(shí)，對(duì)OFDM 識(shí)別率很低，但是在使用相同特征提取參數(shù)的情況下，信噪比大于-2 dB 時(shí)識(shí)別率能夠達(dá)到100%。

圖17 OFDM 波形檢測(cè)準(zhǔn)確率

采取相同的仿真參數(shù)與仿真條件，將本文算法與文獻(xiàn)[21]算法進(jìn)行仿真性能對(duì)比，結(jié)果如圖18 所示。

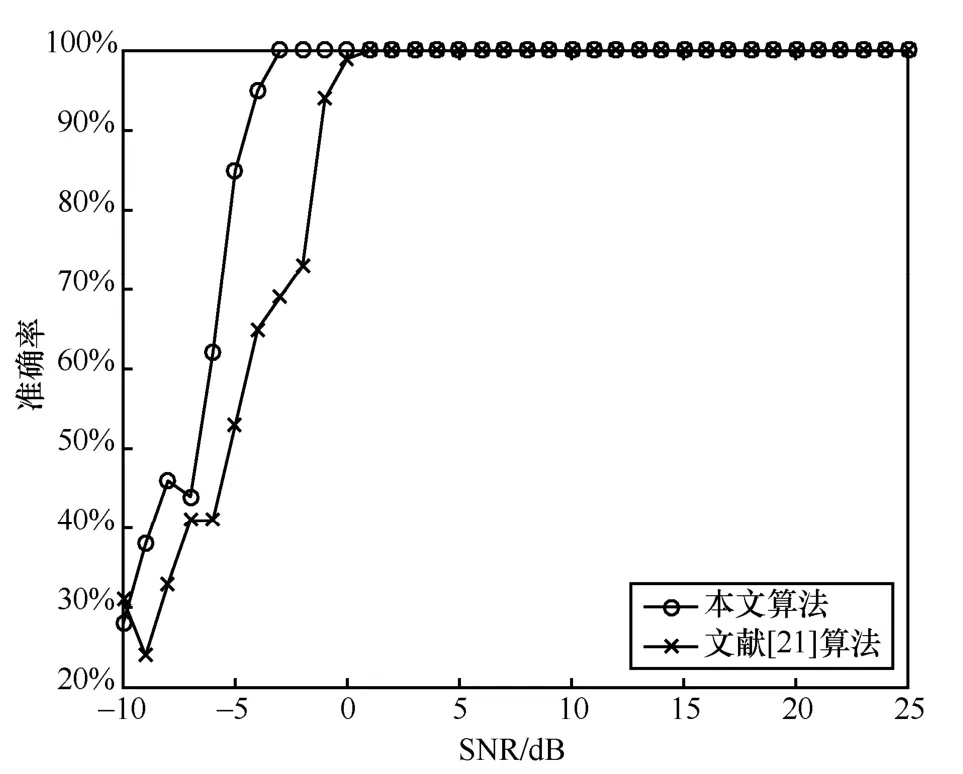
圖18 本文算法與已有算法檢測(cè)結(jié)果對(duì)比

從圖18 可以看出，通過(guò)提取聯(lián)合特征量，在低信噪比下能夠獲得比文獻(xiàn)[21]算法更高的準(zhǔn)確率。

實(shí)驗(yàn)表明，本文選取的聯(lián)合特征參數(shù)能夠在一定情況下忽略信道對(duì)信號(hào)帶來(lái)的多徑以及加性噪聲的影響。在信噪比較大時(shí)，可獲得理想的識(shí)別效果，在一定程度上說(shuō)明，該方法能夠達(dá)到在實(shí)際通信中對(duì)OFDM 信號(hào)檢測(cè)并進(jìn)行應(yīng)用。

為了探討OFDM 符號(hào)數(shù)目對(duì)聯(lián)合特征量的影響，接下來(lái)對(duì)不同數(shù)目時(shí)OFDM 信號(hào)檢測(cè)結(jié)果進(jìn)行仿真，在其他仿真條件不變的情況下，符號(hào)數(shù)目分別取4 270、42 700、427 000，進(jìn)行100 次蒙特卡洛仿真，仿真結(jié)果如圖19 所示。

圖19 不同符號(hào)數(shù)對(duì)OFDM 信號(hào)識(shí)別準(zhǔn)確率的影響

由圖19 可以看到，在相同信噪比的情況下，選取的符號(hào)越多，識(shí)別準(zhǔn)確率越高，且最后都能夠完全識(shí)別。當(dāng)符號(hào)數(shù)到達(dá)一定數(shù)量后，識(shí)別準(zhǔn)確率趨于一個(gè)穩(wěn)定值，不再隨符號(hào)數(shù)量變化而變化。

5.2 OFDM 信號(hào)參數(shù)盲估計(jì)

對(duì)已經(jīng)檢測(cè)出的OFDM 信號(hào)進(jìn)行FFT 運(yùn)算需要知道OFDM 信號(hào)的符號(hào)參數(shù)，包括有效符號(hào)長(zhǎng)度、符號(hào)持續(xù)總時(shí)間和CP 長(zhǎng)度。

在本文的仿真模型中，OFDM 的有效數(shù)據(jù)長(zhǎng)度為52，子載波個(gè)數(shù)為64，當(dāng)保護(hù)間隔為子載波個(gè)數(shù)的時(shí)得到符號(hào)的總長(zhǎng)度為80。在沒(méi)有先驗(yàn)信息的情況下，對(duì)仿真模型產(chǎn)生的數(shù)據(jù)進(jìn)行參數(shù)盲估計(jì)。得到的OFDM 子載波有效長(zhǎng)度估計(jì)仿真結(jié)果如圖20 所示。將圖20(a)放大得到圖20(b)，橫軸為信號(hào)的有效數(shù)據(jù)長(zhǎng)度，可得OFDM 信號(hào)的有效數(shù)據(jù)長(zhǎng)度為64，與仿真模型所選取的參數(shù)一致。

OFDM 符號(hào)的符號(hào)長(zhǎng)度NOFDM是LEN(m)的2個(gè)峰值之間的距離。

OFDM 信號(hào)符號(hào)總長(zhǎng)度估計(jì)如圖21 所示。由圖21 可知，OFDM 符號(hào)持續(xù)總長(zhǎng)度為80，正是仿真模型的OFDM 符號(hào)持續(xù)總長(zhǎng)度。由此可得，CP長(zhǎng)度為16，也符合仿真模型的預(yù)設(shè)。仿真結(jié)果表明，利用CP 產(chǎn)生的自相關(guān)性能夠?qū)崿F(xiàn)對(duì)OFDM 符號(hào)的參數(shù)盲估計(jì)。

5.3 OFDM 信號(hào)子載波調(diào)制識(shí)別

現(xiàn)有研究中，OFDM 信號(hào)的子載波只采用某一種調(diào)制方式，本文在OFDM 信號(hào)中同時(shí)使用了空子載波、QPSK、16QAM。仿真實(shí)驗(yàn)參數(shù)選取如下。

圖20 OFDM 波形有效符號(hào)長(zhǎng)度估計(jì)

圖21 OFDM 信號(hào)符號(hào)總長(zhǎng)度估計(jì)

映射方式為空子載波、QPSK、16QAM，相應(yīng)的子載波個(gè)數(shù)分別為3、30、20。

OFDM 子載波上調(diào)制識(shí)別過(guò)程如下。

首先，從接收的OFDM 信號(hào)中分離出各子載波信號(hào)；計(jì)算每一路子載波信號(hào)的統(tǒng)計(jì)信息，求出各自的C20，由此可判斷空子載波的位置。

然后，計(jì)算各非空子載波的特征參數(shù)Gr，根據(jù)計(jì)算結(jié)果可以判斷調(diào)制方式為QPSK 或16QAM，從而完成子載波調(diào)制識(shí)別。

整個(gè)子載波上調(diào)制方式的識(shí)別流程如圖22所示。

圖22 子載波調(diào)制識(shí)別流程

5.3.1 OFDM 信號(hào)空子載波識(shí)別仿真

在選定特征參數(shù)的情況下，通過(guò)設(shè)置閾值識(shí)別出空子載波。在本文的仿真模型中，空子載波的個(gè)數(shù)為3，且放在子載波前面3 個(gè)的位置。由4.2 節(jié)的推導(dǎo)可知，使用C20可以判斷出子載波上是否為空子載波。從表1 可知，當(dāng)子載波為空子載波時(shí)，C20的值為0；當(dāng)子載波為QPSK 調(diào)制時(shí)，C20的值為1；當(dāng)子載波為16QAM 調(diào)制時(shí)，C20為0.68。由不同調(diào)制方式的參數(shù)結(jié)果不同可識(shí)別出OFDM 子載波中的空子載波，如圖23 所示。可以看出，在信噪比大于0 時(shí)選取的特征參數(shù)C20能夠?qū)⒖兆虞d波的位置及個(gè)數(shù)全部識(shí)別出來(lái)，證明選取該參數(shù)C20進(jìn)行空子載波的識(shí)別是有效可行的。

圖23 OFDM 信號(hào)的空子載波識(shí)別特征參數(shù)C20

5.3.2 OFDM 信號(hào)子載波調(diào)制識(shí)別仿真

在本文仿真模型中，QPSK 調(diào)制的數(shù)據(jù)由傳輸有效數(shù)據(jù)的前30 個(gè)子載波傳輸，而16QAM 調(diào)制數(shù)據(jù)由后20 個(gè)有效子載波進(jìn)行傳輸。對(duì)OFDM 信號(hào)的子載波調(diào)制識(shí)別仿真如圖24 所示。

圖24 OFDM 信號(hào)子載波上調(diào)制識(shí)別特征參數(shù)Gr

本文選取的參數(shù)Gr對(duì)信道帶來(lái)的消極影響不敏感，在參數(shù)C20將子載波中的空子載波識(shí)別出之后，利用4.2 節(jié)的分析可知，參數(shù)Gr能夠在子載波使用QPSK和16QAM 時(shí)有很好的區(qū)分度，由表2 可看出，OFDM信號(hào)中調(diào)制方式為QPSK 時(shí)特征值Gr為16，調(diào)制方式為16QAM 時(shí)，Gr等于13.759。設(shè)置合適的閾值對(duì)OFDM 仿真模型進(jìn)行仿真。從圖24 可知，在信噪比大于7 時(shí)能夠完全將QPSK 調(diào)制的子載波和16QAM 調(diào)制的子載波區(qū)分開(kāi)，達(dá)到了子載波調(diào)制識(shí)別的要求。

6 結(jié)束語(yǔ)

本文以非合作接收處理為背景，對(duì)OFDM 信號(hào)檢測(cè)、符號(hào)數(shù)估計(jì)和子載波上調(diào)制識(shí)別問(wèn)題進(jìn)行了較為詳細(xì)的推導(dǎo)和研究。從理論上論述了OFDM 信號(hào)的產(chǎn)生、OFDM 波形符號(hào)數(shù)的估計(jì)，并針對(duì)通信的復(fù)雜環(huán)境提出一種新的聯(lián)合特征提取參數(shù)進(jìn)行OFDM檢測(cè)，在此基礎(chǔ)上對(duì)包含空子載波和QPSK 以及16QAM映射方式的OFDM信號(hào)使用一種基于特征參數(shù)提取的方法進(jìn)行子載波間調(diào)制方式識(shí)別模型，該模型能夠進(jìn)行OFDM 參數(shù)盲估計(jì)，故不需要先驗(yàn)信息，適合非合作通信中的調(diào)制識(shí)別。仿真結(jié)果顯示該模型能夠很好地實(shí)現(xiàn)OFDM 的信號(hào)的檢測(cè)以及子載波上調(diào)制方式識(shí)別，且運(yùn)算量適中，易于工程實(shí)現(xiàn)。