惠西南地區儲層含油氣性疊前地震固液解耦識別*

宗兆云 孫乾浩 陳維濤 羅 明 賈培蒙 何 葉 衛 哲

（1.中國石油大學（華東）地球科學與技術學院 山東青島 266580； 2.中海石油（中國）有限公司深圳分公司 廣東深圳 518054）

珠江口盆地惠西南H1地區油氣資源豐富，具有多源供烴、多層系含油的特點［1］。其中，惠西南地區位于珠江口盆地珠一坳陷惠西半地塹西南側，是東沙隆起向珠一坳陷的延伸地帶，以構造-巖性復式圈閉勘探為主，產量主要來自珠江組三角洲沉積體系，油氣層為K08—K22。由于該工區疊前數據主頻較低（約25 Hz）、大角度疊前數據信噪比低且目標砂體縱向變化大、巖性圈閉邊界難落實，復式油氣藏延展范圍難落實，常規的流體識別方法難以排除因孔隙度造成的假“亮點”。

地震巖石物理理論搭建了地震資料與彈性參數之間的橋梁，為利用疊前地震資料進行儲層流體識別奠定了理論基礎。地震巖石物理驅動的疊前地震流體識別方法是當今勘探地球物理領域中儲層含油氣性判別的主流方法［2-6］。該方法將與孔隙流體有關的特性表征為流體指示因子，或者基于地震巖石物理構建流體類型與彈性參數的量化關系，并利用地震資料所包含的豐富信息實現流體指示因子的反演或預測［7］，從而達到儲層油氣識別的目的。

針對常規地震反演方法對孔隙流體類型判別精度低的問題，首先基于目標儲層砂體巖石骨架結構、孔隙性質以及流體分布特征，建立了相應的砂泥巖油氣儲層地震巖石物理模型。其次，基于巖石物理分析結果，優選固體解耦等效流體體積模量作為流體指示因子。最終，推導相應的地震反射特征方程，實現了巖石物理驅動固液解耦油氣直接識別。該方法能夠有效避免因巖石骨架孔隙度等物性因素導致的流體識別假象，提高疊前地震孔隙流體判識的精度，降低油氣勘探開發的高風險。

1 地震巖石物理研究

1.1 地震巖石物理建模

惠西南H1地區的K08—K22儲層為砂泥巖儲層，在地震巖石物理建模過程中存在以下3個問題：①輸入礦物模量未知；②泥巖段缺少孔隙度解釋；③Xu-White模型干燥巖石孔隙縱橫比不變。本文采用3種策略解決相應的問題：①建立巖石彈性模量與巖石物性參數關系式，使飽和巖石模量誤差最小，得到最優礦物組分模量，對相同層位進行多井統計估算；②利用測井數據約束反演孔隙度；③利用DEM模型［8-10］和K-T模型［11］建立變孔隙縱橫比的干燥巖石。改進的砂泥巖模型除考慮了砂巖和泥巖影響，考慮到實際巖石中的孔隙縱橫比不是固定的，形成了一套變孔隙縱橫比的碎屑巖地震巖石物理模型來計算巖石的宏觀彈性模量（圖1）。

圖1 基于巖石物理模型的巖石彈性模量估算Fig.1 Estimation of elastic modulus based on rock physical model

在惠西南H1地區復雜含油氣儲層巖石物理模型構建的基礎上，利用已有的測井解釋曲線，如礦物含量、孔隙度、泥質含量以及含水飽和度等，采用測井約束反演修正方法對靶區的橫波速度數據進行估算，并與實測橫波數據進行對比來驗證巖石物理模型的合理性和有效性。針對不同巖性的目標儲層，選擇性地采用相應的模型來實現關鍵井的橫波速度估算。圖2為W1井縱橫波速度估算結果，可以看出，本方法預測的橫波速度與實測的橫波速度吻合很好，說明該巖石物理模型的合理性。同時發現在目標層處仍能夠預測較為準確的縱波速度和橫波速度，預測誤差大概在10%以內，在可接受范圍內。

1.2 巖石物理分析

基于1.1節構建的地震巖石物理模型，對H1地區進行多參數巖石物理交會分析，選出幾個較好的彈性參數作為備選參數，對工區內W1井的巖性進行交會分析。圖3為不同彈性參數交會分析結果，可以看出，砂巖顯示為低彈性阻抗（小角度部分疊加）和低密度，泥質砂巖顯示為較低的彈性阻抗，2個參數都可以區分砂巖和泥質砂巖，并能識別砂巖，為開展彈性阻抗反演提供了巖石物理理論支撐。圖4為W1井的流體參數交會分析結果，可以看出，固液解耦等效流體體積模量Kf能夠區分水層和油層。

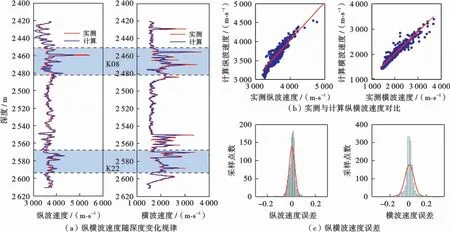
圖2 H1地區W1井縱橫波速度估算結果Fig.2 Results of the estimated P-wave and S-wave velocity of Well W1 in H1 area

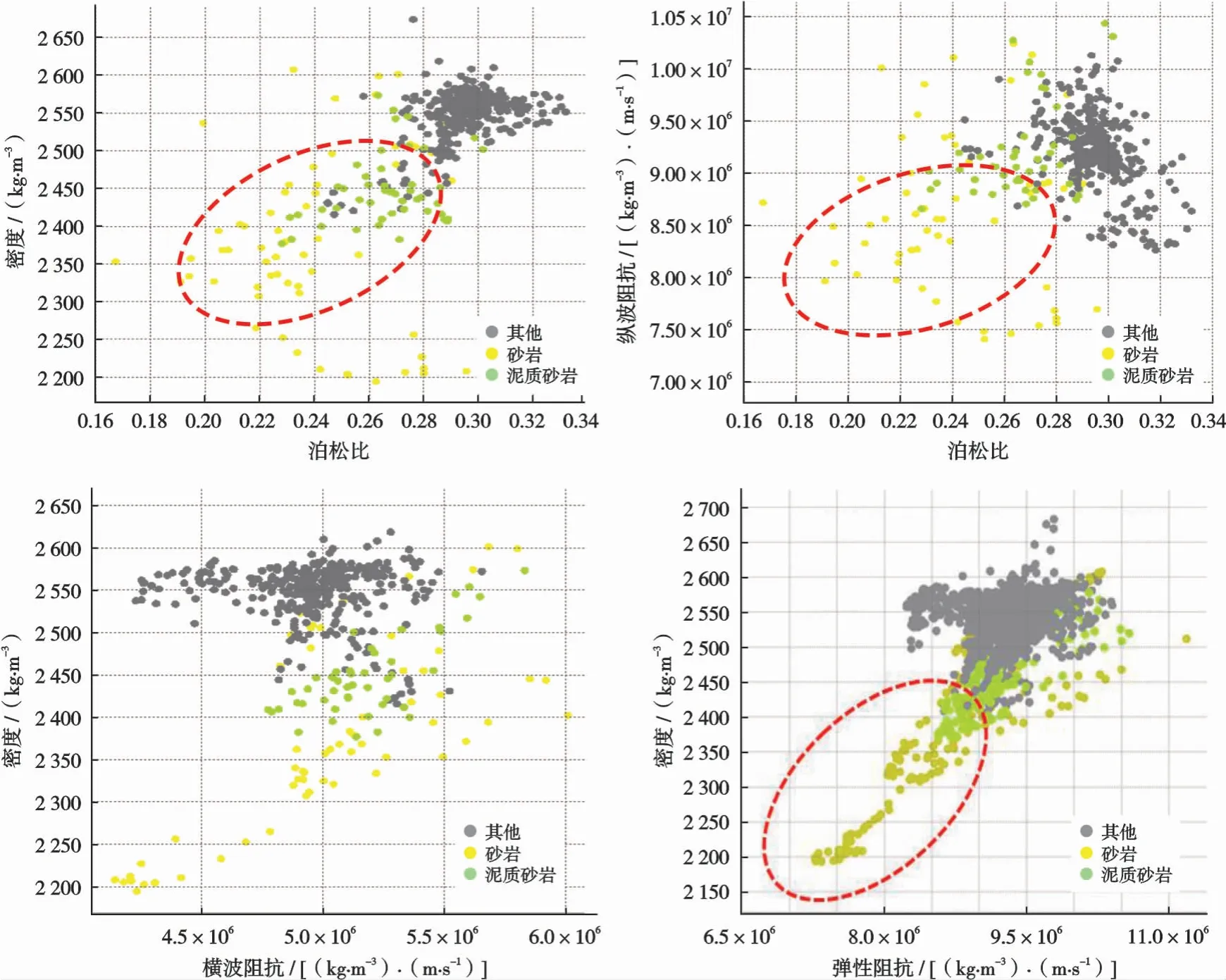
圖3 H1地區W1井不同彈性參數交會結果Fig.3 Intersection results of different elastic parameters of Well W1 in H1 area

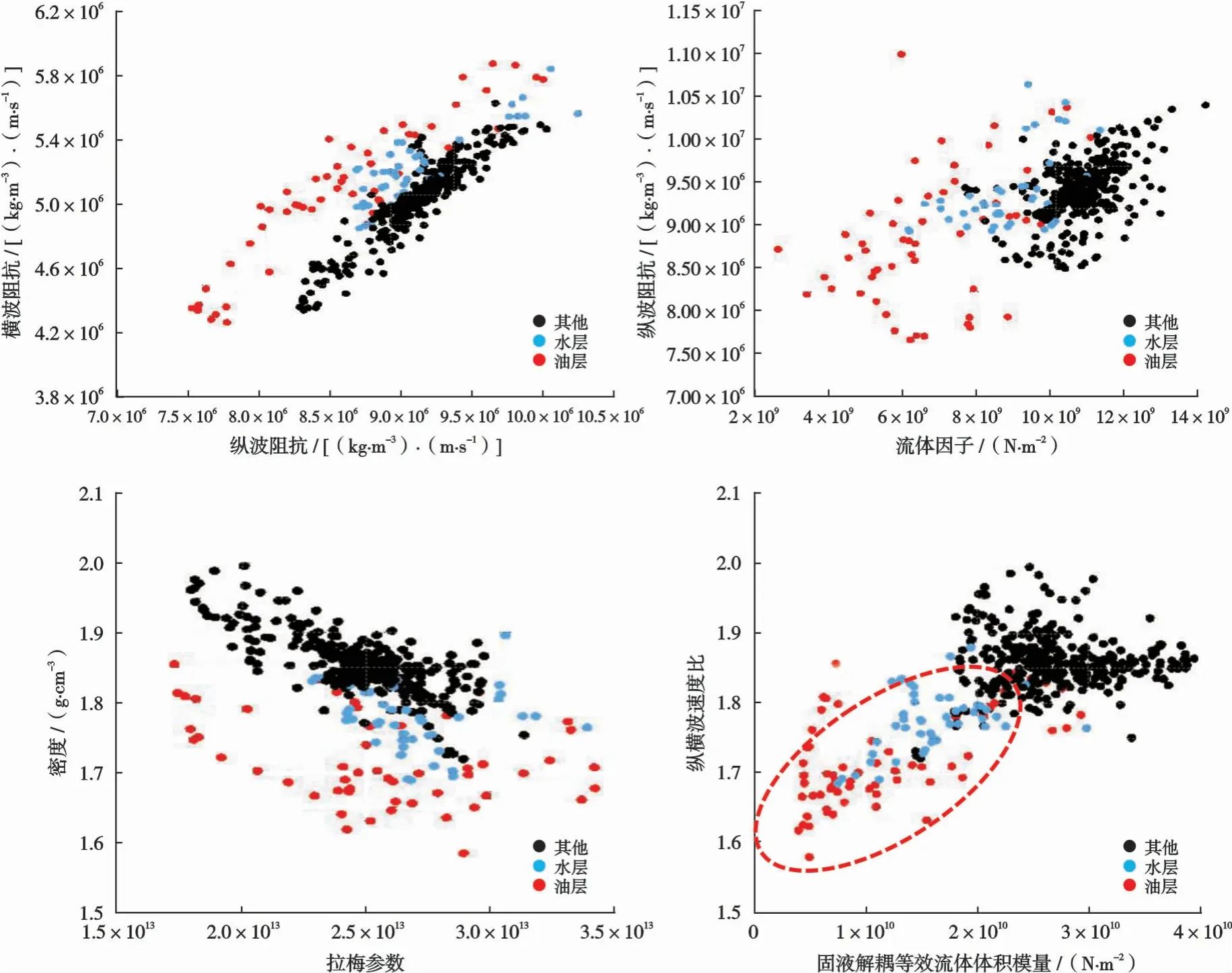
圖4 H1地區W1井不同流體參數交會結果Fig.4 Intersection results of different fluid parameters of Well W1 in H1 area

1.3 儲層敏感性參數分析

針對惠西南H1地區的優質儲層評價領域，成熟油區目前以構造-巖性復式圈閉勘探為主，常規的地震勘探手段往往不夠可靠穩定。首先需要選擇對目標儲層流體反映敏感的彈性參數，這對儲層預測和流體識別意義重大，選定合適的參數可以減小地震優質儲層評價的不確定性和多解性。圖5對W2井彈性參數和儲層物性參數進行了對比分析，彈性參數：①K22層油氣砂體VP降低明顯；②K22層彈性參數穩定；③密度明顯降低；④固液解耦等效流體體積模量Kf遞低（漸變模式）。儲層物性：①K22層有效孔隙度約8%～20%；②K22層水飽和度10%～95%；③K22層氣層物性較好。

一般情況下，流體類型的檢測具有多解性，因此，需要選擇對流體敏感性高的彈性參數作為流體指示因子。此處，利用測井中橫波信息，對目標工區的彈性參數進行流體敏感性分析，流體的敏感性可根據下式計算：

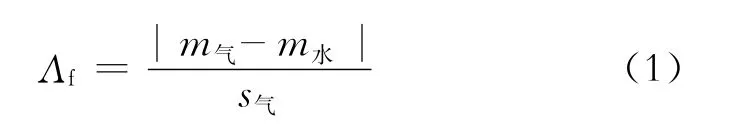
式（1）中：Λf表示彈性參數對流體的敏感系數；m氣為含氣層的彈性參數值；m水為含水層的彈性參數值；s氣為含氣層的彈性參數標準差。

目標工區的流體敏感性分析結果如圖6所示，IS為橫波阻抗，VS為橫波速度，λρ為拉梅參數和密度的乘積，μρ為剪切模量與密度的乘積，f為Gassmann孔隙流體項，σ為泊松比，VP為縱波速度，IP為縱波阻抗，Kf為固液解耦等效流體體積模量。通過流體敏感性對比分析可知，固液解耦等效流體體積模量Kf在區分水層和氣層方面具有最大的潛力。

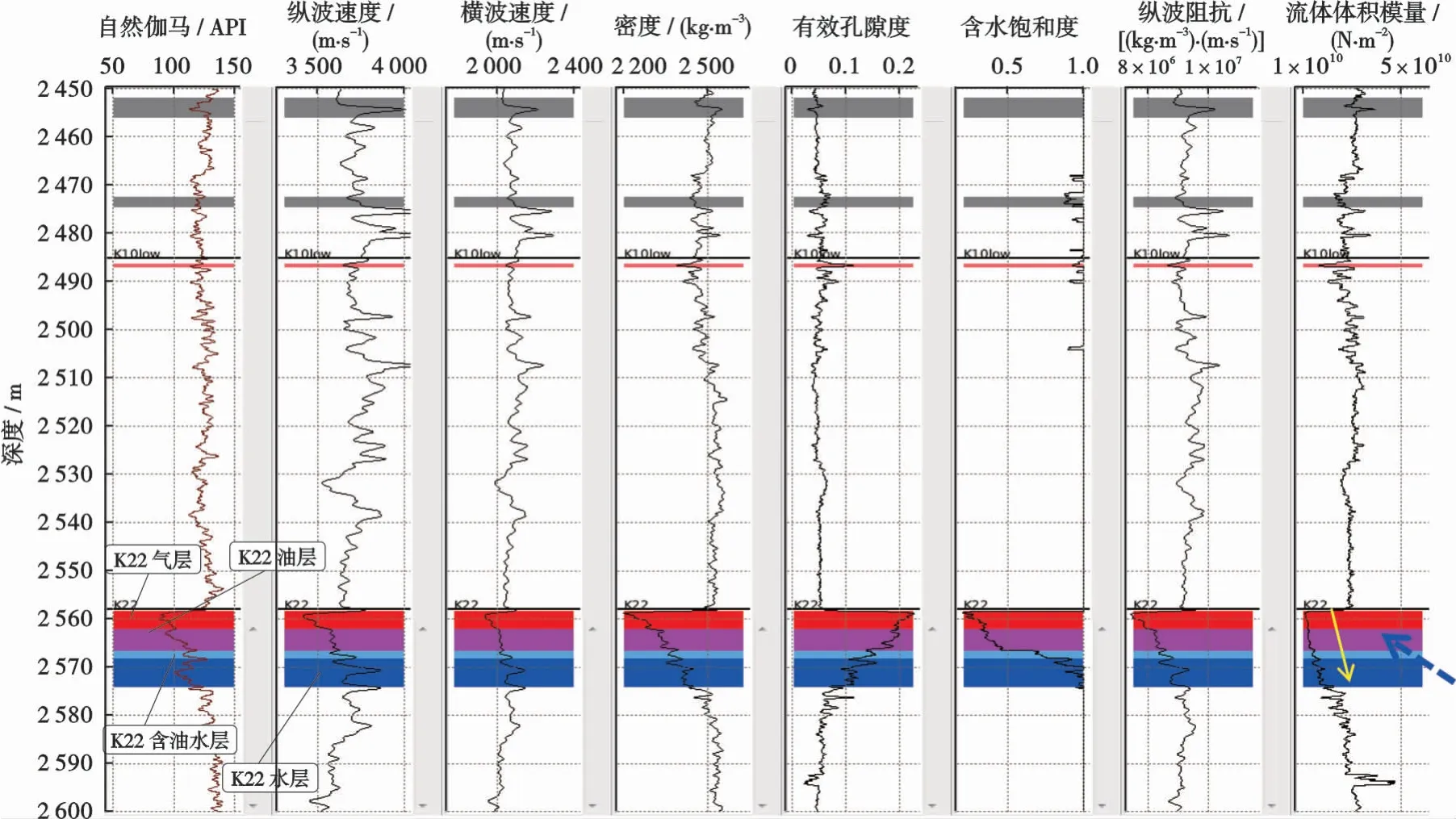
圖5 H1地區W2井彈性參數和儲層物性參數分析Fig.5 Analysis of elastic and physical parameters of Well W2 in H1 area

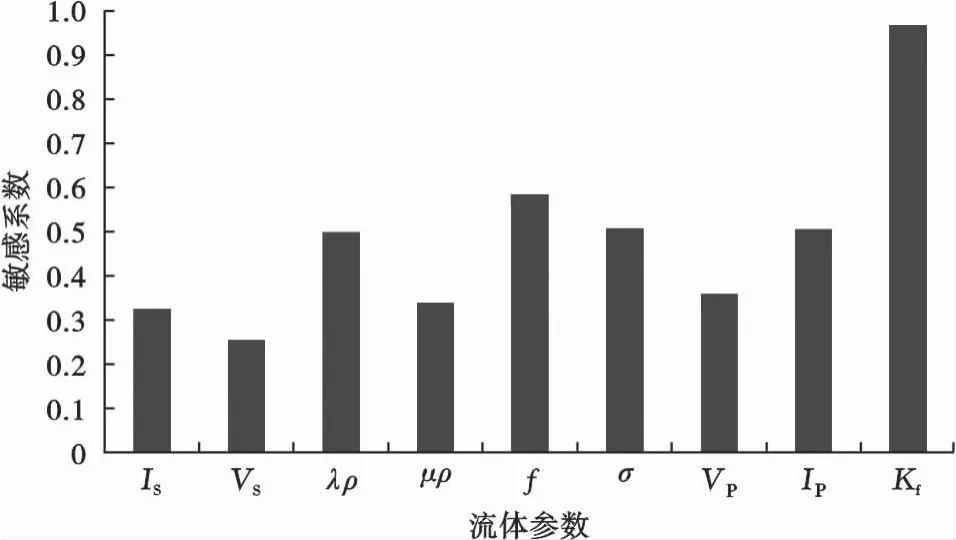
圖6 H1地區地震巖石物理流體參數敏感性對比分析Fig.6 Comparative analysis of sensitive of the rock physical fluid parameters in H1 area

2 固液解耦等效流體體積模量直接提取

基于構建的地震巖石物理模型，對含流體儲層進行正演模擬分析，獲取流體的地震響應特征，并將這種響應特征表征為流體指示因子，用于地下儲層流體類型的識別。因此，構建物理意義明確且對流體敏感性高的流體指示因子具有重要意義。

雙相介質理論因其能夠更好地表征孔隙流體的彈性特征而被廣泛應用于流體識別中。Russell等在消除了密度項的影響后［12］，直接給出Gassmann流體項f的表達式，即

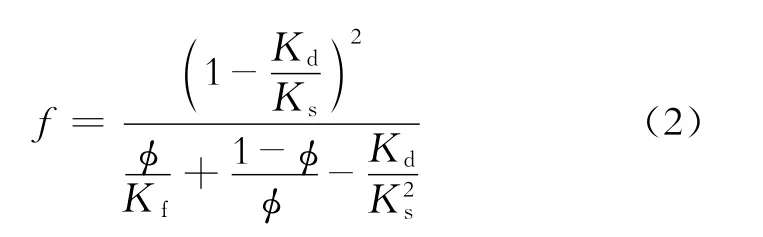
式（2）中：Kd為巖石骨架的體積模量，Ks為巖石基質的體積模量，Kf是固液解耦等效流體體積模量，對于有多相流體則可以利用Wood公式進行計算，計算公式為，Ko、Kg和Kw分別表示油、氣和水的體積模量；So、Sg和Sw分別表示含油、氣和水飽和度，且Sw+So+Sg=1。

通過分析式（2）可以發現，Gassmann流體項f不僅與流體的彈性特征有關，還受巖石固體參數（剛性參數）的影響，例如，礦物基質模量、干巖骨架模量以及孔隙度等，即固體相和液體相的彈性特征是耦合的。Dehua Han和Batzle等［13］利用統計巖石物理對碎屑巖進行了分析，研究了Biot-Gassmann理論中孔隙流體與巖石骨架間的耦合關系，將固液解耦等效流體體積模量Kf從耦合關系中解耦出來得［4］

基于臨界孔隙模型的巖石物理經驗公式［13-15］，得AVO線性近似公式為［4］

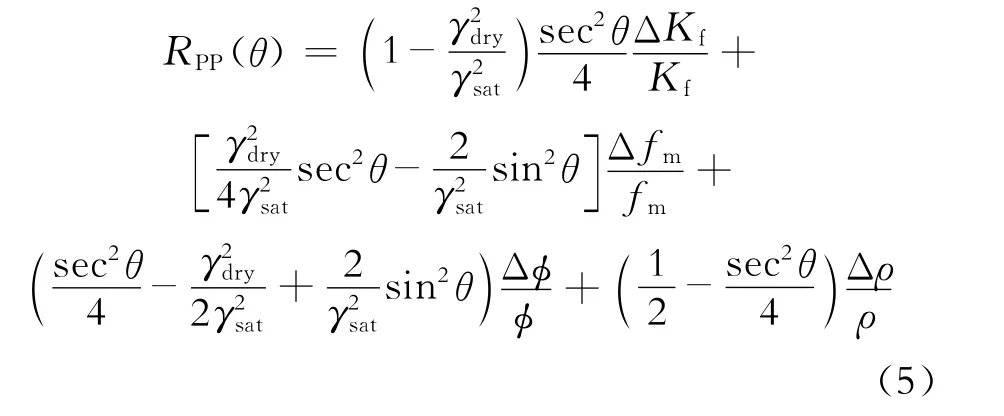
式（5）中：fm=φμ為固體剛性參數；γ2dry與γ2sat分別為干巖石與飽和巖石的縱橫波速度比的平方；Kf為介質的固液解耦等效流體體積模量；μ為介質的剪切模量；ρ為介質的密度；φ為介質的孔隙度。借鑒Connolly推導彈性阻抗的思想［16］，用彈性阻抗表示為

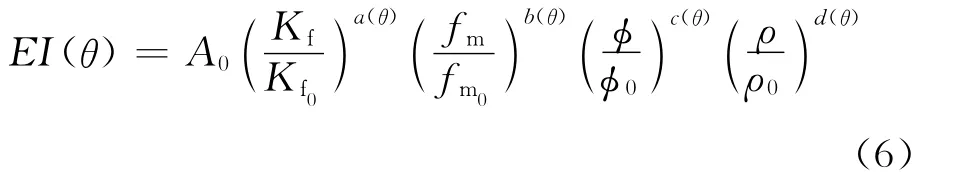
式（6）中：A0是標準化因子，具體表達式為

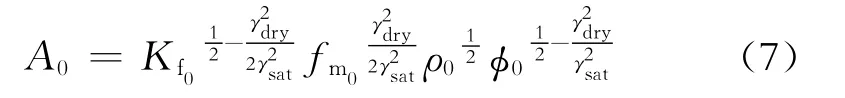
由式（7）可知，當入射角θ=0時，彈性阻抗與波阻抗的值相等，當入射角非零時，彈性阻抗數值發生變化，但其量綱仍然與波阻抗保持一致，為后續參數提取提供了保證。

彈性阻抗數據體的獲取是彈性參數提取第一步，通常彈性阻抗數據體可通過常規的疊后地震反演來獲取，獲得彈性阻抗數據體后，需要利用式（6）對彈性參數進行提取。經過標準化的彈性阻抗方程如式（6）所示，為了簡化求解方法，對公式進行對數變換，將其轉化為線性形式［7］

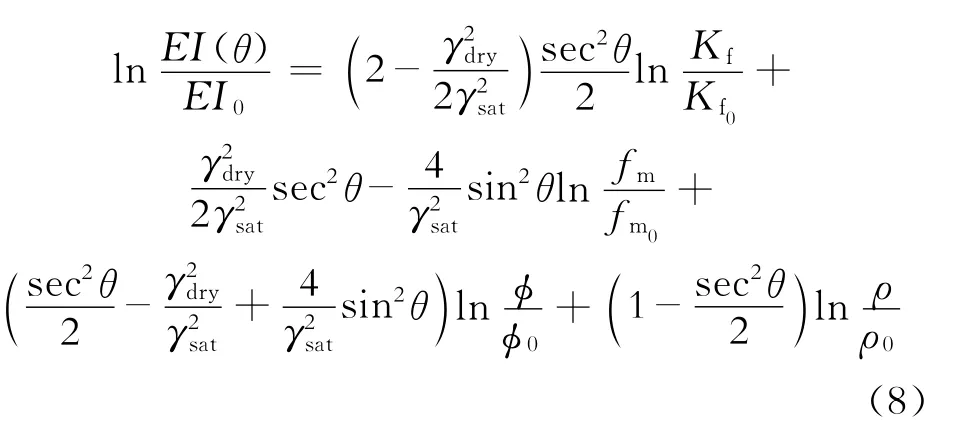
其中：EI0=A0。

根據式（8），在獲得彈性阻抗數據體以及孔隙度數據體時，利用

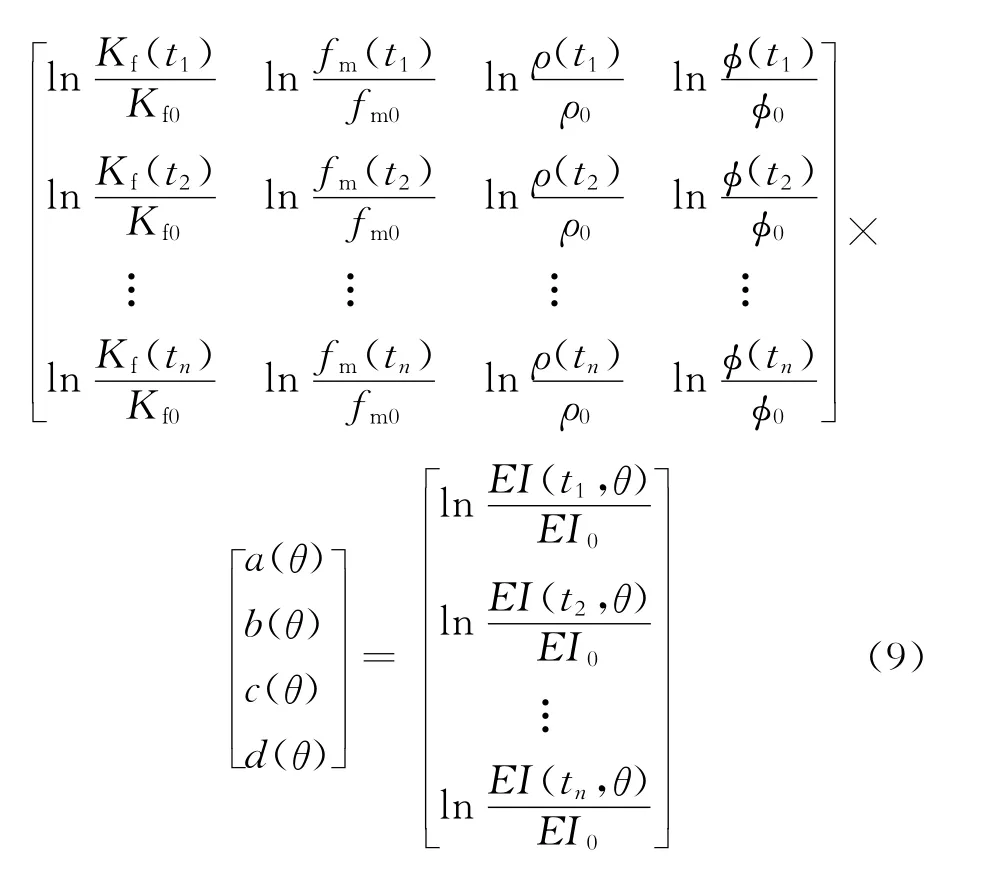
求解以上矩陣，即可獲得適用于研究工區的系數a（b）、b（θ）、c（θ）和d（θ）的數值，n為每一道對應的參數個數。針對不同的入射角度分別計算，便可得到4個角度（分別為θ1、θ2、θ3和θ4）對應的16個系數，即a（θ1）、b（θ1）、c（θ1）、d（θ1）；a（θ2）、b（θ2）、c（θ2）、d（θ2）；a（θ3）、b（θ3）、c（θ3）、d（θ3）；a（θ4）、b（θ4）、c（θ4）、d（θ4）。

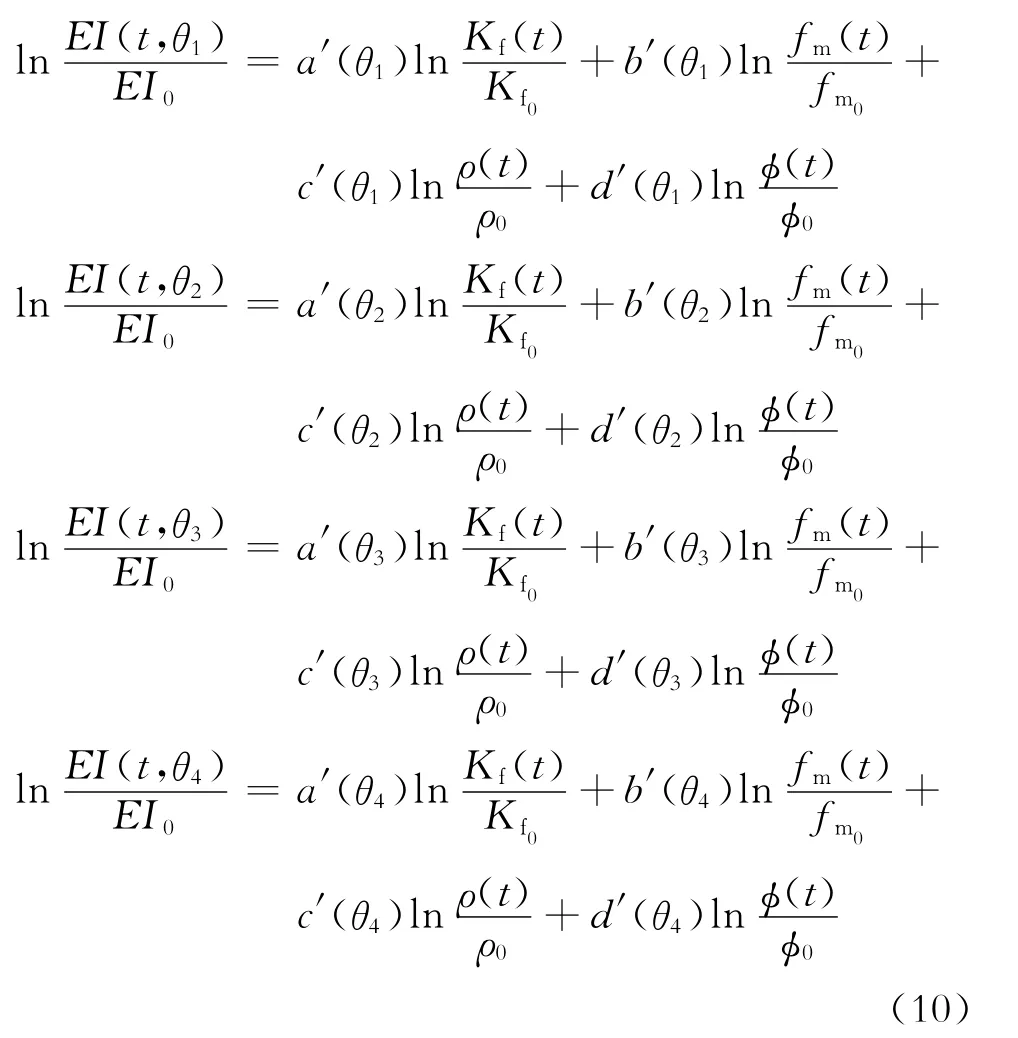
將16個系數代入方程組（10），可得到任意采樣點處的固液解耦等效流體體積模量、固體剛性系數以及密度參數。

3 實例應用

為了避免通過縱、橫波速度間接計算導致的誤差累積，基于式（6）開展了固液解耦等效流體體積模量直接提取的彈性阻抗反演方法。圖7為過6口井的部分角度疊加地震剖面。A井K08層為干層，K22up層為氣水界面，K22為油層；B井K08層為含氣水層，K22up層為差氣層，K22為氣層；C井K08層為油水，K22層為含油水層；D、E、F井發育氣層。

圖8為彈性阻抗的反演結果，可以看出彈性阻抗在6口井儲層發育位置顯示出明顯的低值異常，砂巖顯示低值異常，彈性阻抗會隨著泥質含量的增高而增高，泥質砂巖彈性阻抗值較砂巖和含泥砂高。 圖9為反演的彈性阻抗直接提取的固液解耦等效流體體積模量剖面，可以看到含氣區顯示明顯的低值，含油區低值程度次之，含水區低值程度較弱，這一結果與測井解釋結果吻合，證明基于固液解耦等效流體體積模量的疊前地震直接提取方法不僅可以有效識別儲層，還可以識別流體類型。

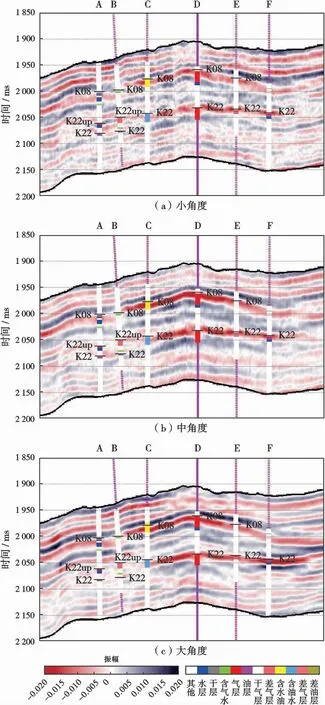
圖7 H1地區部分角度疊加地震剖面Fig.7 Seismic profile of partial angle stack of H1 area

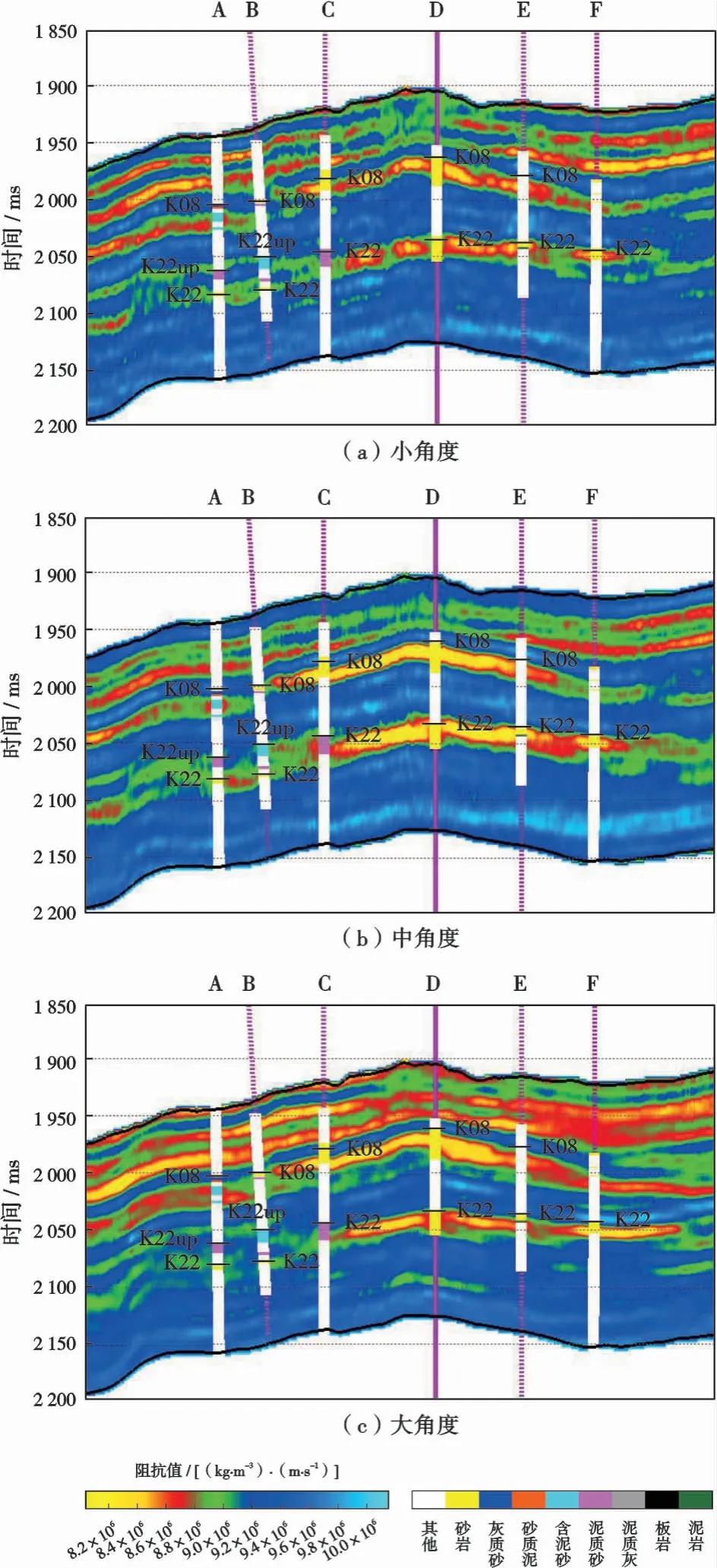
圖8 H1地區彈性阻抗剖面Fig.8 Elastic impedance of H1 area

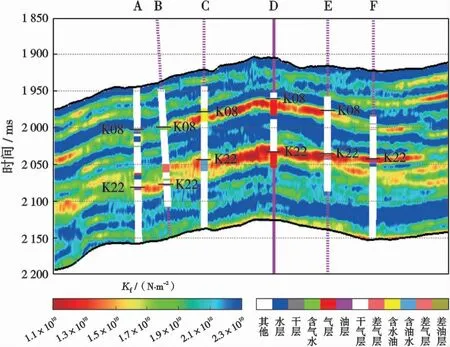
圖9 H1地區固液解耦等效流體體積模量剖面Fig.9 Profile of solid-liquid decoupling fluid factor of H1 area

圖10為沿K22層提取的小角度彈性阻抗均方根切片，為H1地區儲層砂體展布范圍。圖11為沿K22層提取的固液解耦等效流體體積模量均方根切片，為預測的流體展布范圍。可以看出，惠州D井區域有較強的能量響應，發育大范圍儲層并具有含流體性，與實際鉆井結果吻合。惠西南地區發育部分儲層，具有一定的含流體性。預測結果與地質認識吻合，證明了該方法對于儲層刻畫和流體識別的有效性。

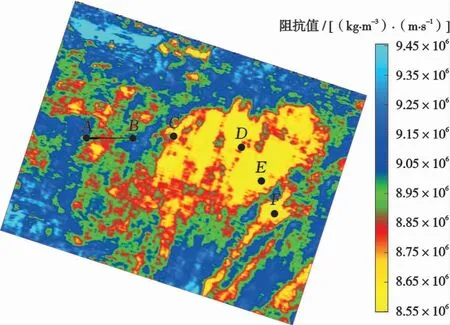
圖10 H1地區沿K22層提取的小角度彈性阻抗均方根切片Fig.10 RMSslice of small angel elastic impedance along K22 layer of H1 area

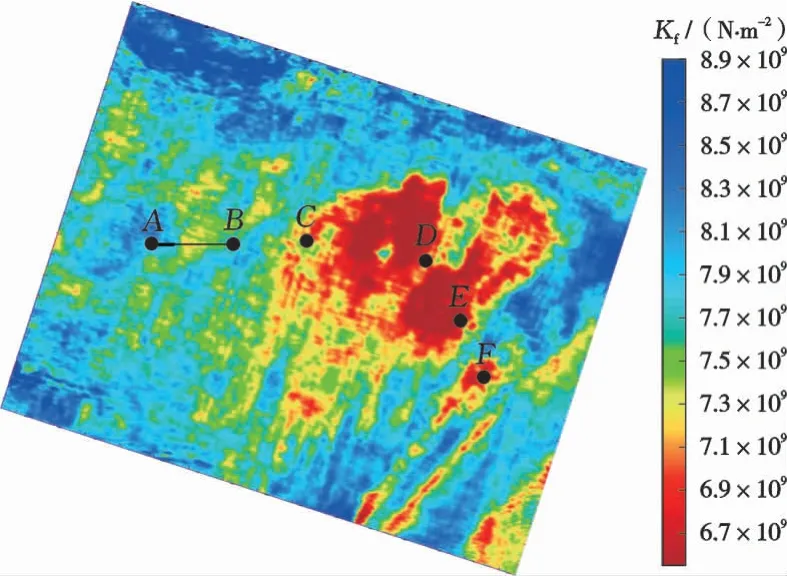
圖11 H1地區沿K22層提取的固液解耦流體因子均方根切片Fig.11 RMSslice of solid-liquid decoupling fluid factor along K22 layer of H1 area

4 結論

1）在分析該工區巖石物理特征的基礎上，構建了符合工區特點的變孔隙度砂泥巖巖石物理模型，并采用了基于測井約束反演修正的橫波預測技術進行橫波預測，預測橫波與實測橫波吻合，證明巖石物理模型的有效性。

2）通過地震巖石物理交會分析，對不同參數的巖性以及流體敏感性進行分析，認為小角度彈性阻抗和固液解耦流體因子可作為敏感性儲層和流體參數，為儲層描述和流體識別工作提供了有力支撐。

3）本文基于彈性阻抗利用直接反演的思想，實現了固液解耦流體體積模量的直接提取。該方法綜合利用了地質信息、測井數據以及疊前地震AVO信息，既保證了常規彈性阻抗反演的抗噪性，又避免了間接反演的誤差累積和孔隙度等物性的影響，可以更有效地識別儲層及流體類型。