基于融合算法的GM(1,1)模型在碼頭監測中的應用

遠 航，鄭成明

（青島港國際股份有限公司 港建分公司，山東 青島 266409）

引 言

碼頭是港口裝卸生產的主要設施，其安全穩定是保障安全作業的必要條件。由于受到海浪、風力、船舶擠靠力等多類型荷載的作用，兼受水文、氣象條件眾多因素影響，碼頭在服役期間，結構往往會產生破損、老化，受力狀態與設計服役條件產生偏離，形成安全隱患。

為保障服役期間碼頭安全，其結構變化形態能被及時察覺，碼頭監測已成為港口運行過程中必不可少的重要環節。根據監測結果對穩定狀態進行合理預測，并將預測結果及時反饋，對于避免碼頭失穩、周邊建筑物及地下管線破壞，及時排除險情，保障裝卸作業安全具有重要意義。

碼頭的穩定性受環境、水文、地質、氣候、施工等多種因素的綜合作用，其中有的因素具有確定性，但更多的體現了隨機性、模糊性、可變性等特點，具有明顯的灰色特征，因此，可采用灰色系統理論對碼頭變形進行預測。灰色系統理論[1]以部分信息已知，部分未知的不確定性系統為研究對象，通過對已知信息的充分挖掘，累加處理原始數據，并進行微分求導后對未知數據進行預測，從而有效識別系統整體狀態。

碼頭監測數據符合灰色模型時間序列數據要求，可以通過建立灰色動態 GM(1,1)模型對碼頭的未來變形進行預測。在我國，已經有眾多學者采用灰色理論對碼頭、基坑及大壩等結構物位移進行預測。郭健寶[2]等建立了某重力式碼頭沿岸水平位移的 GM(1,1)預測模型，證明了該理論用于碼頭變形預測是切實可行的。張印濤等[3]對常規GM(1,1)模型進行改進，成功應用于基坑變形預測，進一步提高了預測精度。王在泉[4]考慮了數據在時間軸上的不同權重，建立了不等時距的GM(1,1)模型，對某邊坡位移進行了預測分析。

灰色系統理論在數據預處理過程中，有時難以區分有效數據與噪聲信息，從而影響預測精度。為改善模型性能，提高預測精度，有學者引入置信距離、支持度等概念，采用融合算法對數據進行預處理，從而有效區分噪聲與信息，以提高預測精度[5-8]。但上述算法在計算支持區間時，均面臨置信距離的界限取值問題，不同的界限值對于計算結果有著直接影響，并降低預測結果的可信度。

針對上述缺點，本文采用的融合算法根據初始數據之間的差值構建支持度矩陣，并以此為基礎構建權重矩陣，充分利用數據的原始信息，不必預先設定界限值，降低了人為處理數據的主觀性，提高預測模型的準確性。

本文采用 GM(1,1)模型，對碼頭監測數據進行預測，并生成多個預測值，結合加權融合算法，對這些預測值進行融合，形成最終預測值，對青島港某高樁碼頭的位移進行預測分析，驗證了算法的有效性和準確性，具有良好的應用價值。

1 灰色系統建模

1.1 建模

GM(1,1)模型的適用條件是目標數列符合光滑離散函數的基本特征，即：

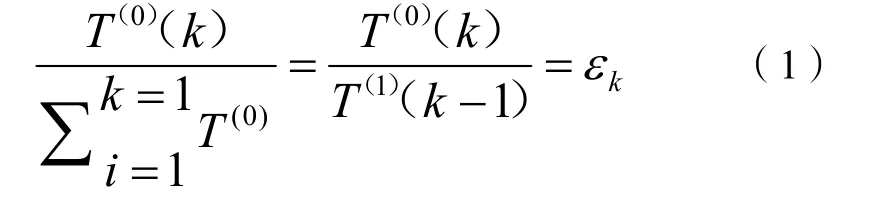
當k≥3時εk=｛ε3,ε4,…,εn｝為遞減數列，且0≤εk≤1，若k趨向于+∞，εn的數值趨向于0時，則X(0)可稱之為光滑離散函數。其中，εk的遞減速度越快，則意味著T(0)光滑性越好。

在獲取初始數據序列T(0)時，不可避免受到外界因素的干擾，從而導致光滑性出現隨機擾動。可通過采用累加生成（AGO）法進行處理，處理后的數據可在一定程度上去除隨機擾動。

若原始數列記為：

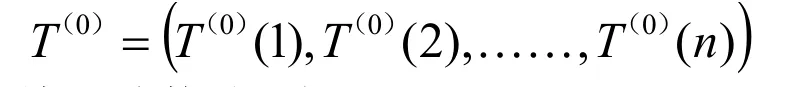
累加生成數列記為：

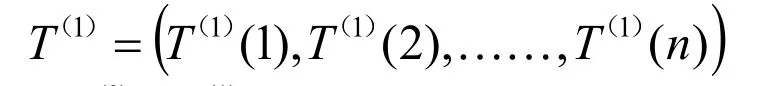
并且X(0)與X(1)滿足：

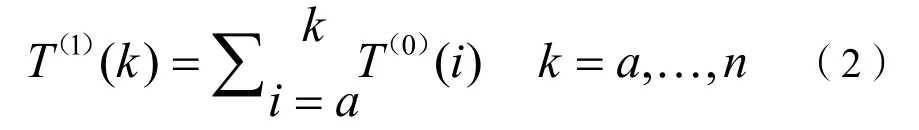
若經處理后的數列T(1)仍具有較明顯擾動，則可以通過多次累加處理，以保證其光滑性：

對處理后的數列建立微分方程：

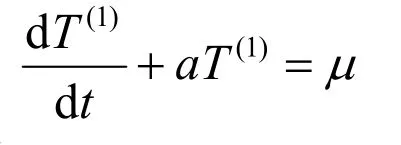
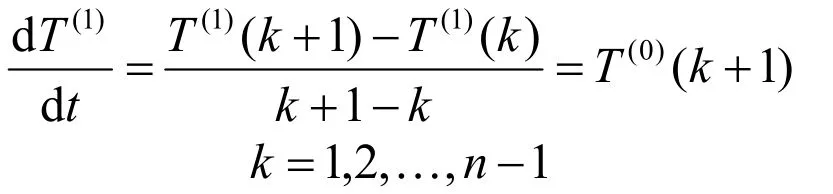
采用最小二乘法求解，得：

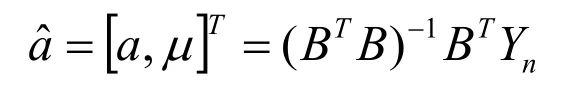
其中：

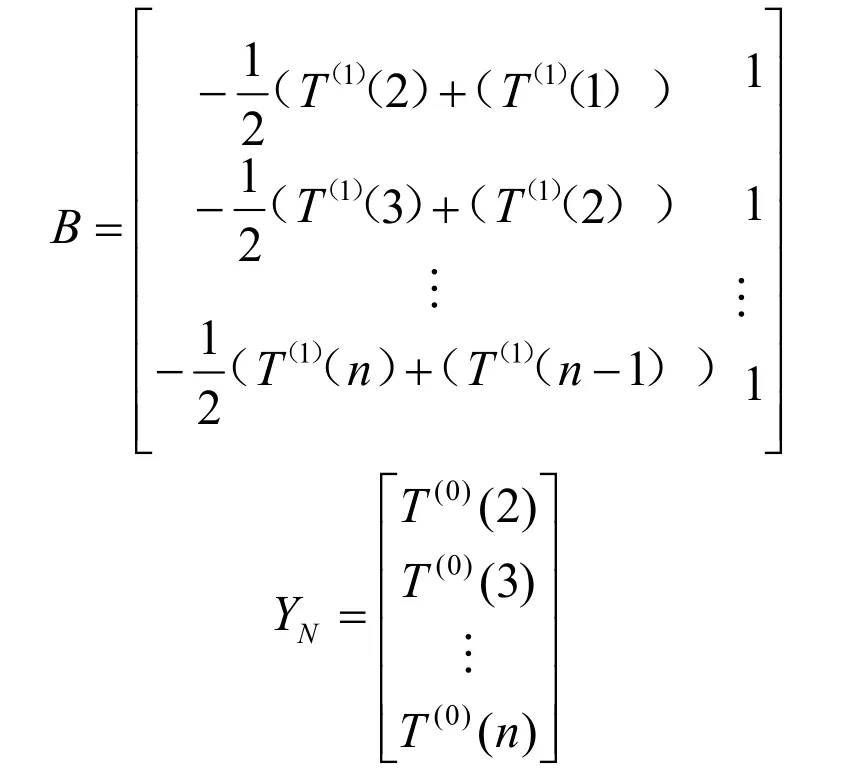
可以推導解出微分方程的解：

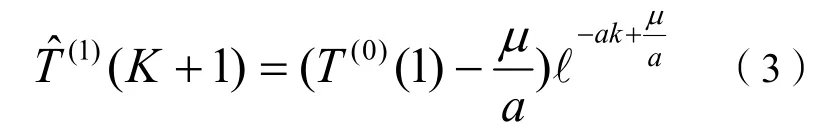
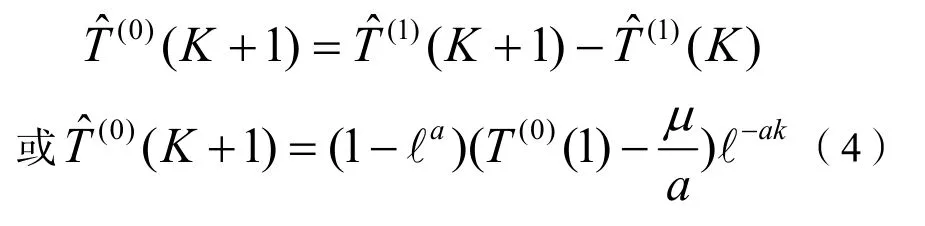
在實際應用當中，可以通過實測數據，建立灰色模型，利用有限樣本在k≤n時進行模擬，并將k推廣到k＞n的情況，此時即為模型預測值。

1.2 加權融合算法

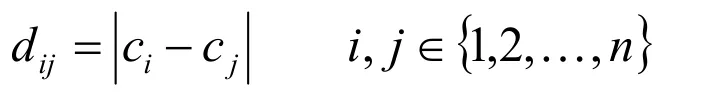
并做如下定義：

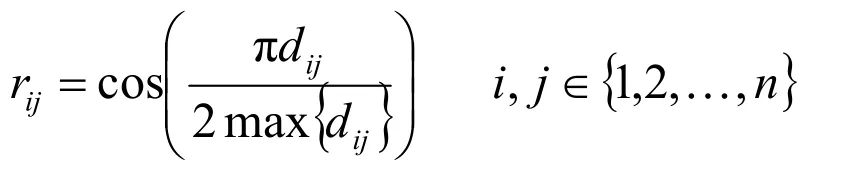
rij為數列C中任意兩個數值的支持度，且符合下列條件：

1）ci,cj數值相差越大，則其支持度越小。

2）rij∈［0,1］。

在先期得到數列C后，進一步計算得到每個ci的權重ωi，ωi應體現出相互之間支持度。

構造矩陣W=RV，W、V分別為由ωi和vj組成的列向量，R為非負對稱矩陣，并滿足，V存在最大特征值λ，與其對應的特征向量為則

經過上述方法與數列C中的其他數據融合后，便可求得融合后的解。

2 碼頭位移監測實例分析

2.1 工程背景

青島港木質高樁碼頭主要建于1901～1906年。碼頭結構組成為鋼筋混凝土前板樁、木質高樁、混凝土承臺等構件。

以青島港某高樁碼頭泊位為例，碼頭頂面高程為6.2 m，混凝土承臺底面高程為0.8 m，叉樁選材為美國紅松，樁長12～15 m，直徑約40 cm，上部嵌入承臺1～3 m不等，下部穿越表層淤泥層及黏土層，直至堅實持力層，斜率為4:1，前后傾斜交叉成樁，木樁前后間距1 m，側向間距1.5 m。

由于服役時間較長，期間部分混凝土構件破損，鋼筋銹蝕嚴重，木樁腐爛蟲蝕，板樁斷裂，碼頭填料也出現了不同程度的掏刷，分別于1948年和1983年進行改造加固，重新打設前板樁，并水下澆筑混凝土，使新板樁與原碼頭連接成整體，并將3.0 m以上部位改為混凝土胸墻，改造后碼頭兼有高樁碼頭及重力式碼頭特點。由于碼頭服役長逾百年，期間經多次改造加固，碼頭的結構型式已經與原設計發生較大變化。構件經過百余年的腐蝕、老化、變形，出現了不同程度的損傷，碼頭結構受力特征難以用數學模型準確描述。

基于上述情況，碼頭服役雖已經超過百年，但由于實際需求，仍需進行部分裝卸作業，為保障碼頭正常裝卸生產，確保安全作業，在碼頭受力不明確、構件損傷程度存在差異、環境復雜、外部條件難以充分掌握的情況下，對碼頭進行位移觀測，并采用灰色模型對碼頭位移觀測值進行預測分析，不失為一種直接簡便、易于操作的方法。

2.2 監測方案

為了測定作業期間碼頭岸線向海方向產生的絕對位移，沿岸線呈直線布設5個觀測點，測點之間距離30 m。以后方陸域的控制點D為基準點，測得方位角和距離，采用極坐標法測定其中某一觀測點Ti的坐標，并以該點為基準線的工作基點。然后將經緯儀挪至Ti點，后視D點，撥水平角α1，建立一條光學視準線。根據觀測點相對于視準線的偏離值，便可得到岸線上觀測點向海方向的水平位移值。如圖1所示。

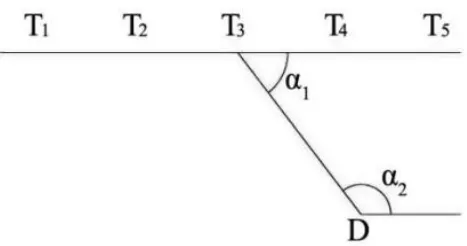
圖1 觀測點平面布置

對測點進行長期觀測，每月大潮低潮位時觀測一次，從而得到碼頭岸線各個測點位移的時間序列。

2.3 監測結果分析

選擇其中2個代表性測點T1和T5點，以最近連續觀測的共計55個數據為樣本進行預測。結果表明，由于在觀測期間碼頭存在持續裝卸作業，觀測點T1、T5的位移總體均呈現階段性增長的態勢，最大值分別為29.1 mm和24.7 mm，如圖2所示。碼頭前沿線位移總體上呈現向海側單調遞增的趨勢，個別觀測數據存在波動，可能由于觀測期間波浪、潮位、風力等外部因素影響所導致。兩個觀測點的位移大致同步，表明在相同的結構型式和外部荷載條件下，碼頭前沿線產生的位移趨勢相同。但由于構件損傷、荷載分布及周邊土體等因素的差異性，位移并不完全等值。

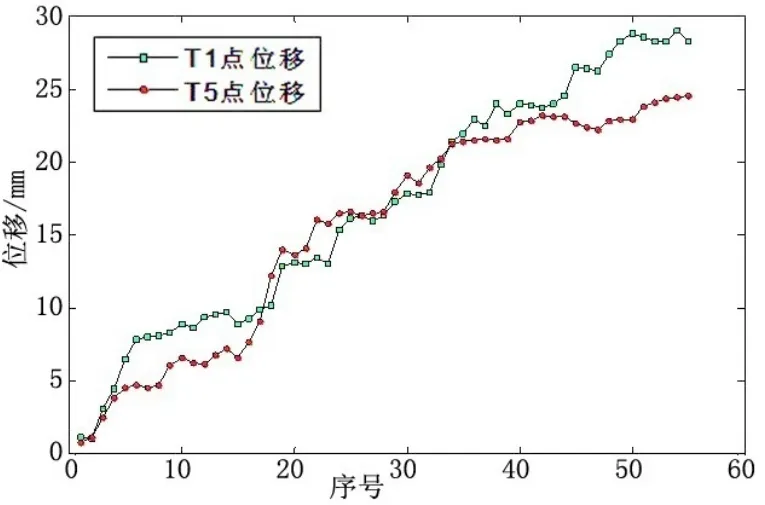
圖2 T1、T5的時間-位移曲線

根據觀測數據，測點處位移尚未達到主動土壓力的極限狀態，位移的階段性增長可能是由于在較大外荷載的情況下，碼頭結構出現塑性變形，導致向海一側的位移發生變化，并引起結構內部的內力重分布，在內力調整之后，結構物與周邊土體形成了新的平衡，位移不再進一步發展。當新的荷載超過結構所能承受的極限荷載時，又會導致新一輪的位移發展與內力重分布。

僅從位移絕對數值來看，碼頭的自穩性尚屬可控狀態，但由于其持續發展的態勢，應對碼頭的結構安全性予以高度關注。

由于本文僅對碼頭前沿線橫向位移這一單一指標進行觀測，不能具體反映出這一指標是由于碼頭整體側移或構件傾斜等原因所導致的，若需進一步明確位移產生原因，還需對碼頭進行整體的位移、形變、構件損傷程度、回填料漏失情況等全方位的健康監測，并結合水文、氣象及裝卸荷載等條件進行分析，明確位移發生的各項原因，以便后期采取針對性措施進行加固。

2.4 位移預測

根據已有的兩組觀測數據對下一月位移進行預測，可先對要預測日期之前的第41、42、…、55個數據分別進行預測，這樣對每個測點均可得到15個預測值，然后對這15個預測值進行融合處理，得到最終的預測值。如要預測第 56個月的位移值，需要采用第10～55、第9～55、…、第1～55個數據分別建模預測，得到15個預測值，然后對結果進行融合。由于觀測數據在時間軸上并非嚴格單調遞增，需對數據進行多次累加生成預處理以滿足模型計算條件。對T1、T5點的觀測值采用上述方法進行預測，并與實測數據對比，結果如表1。

表1 預測結果比較

通過預測值與實測值的對比可以看出，在對多個預測值進行加權融合處理后，可有效去除環境噪聲，而保留真實位移信息，避免了灰色模型處理過程中將真實信息與噪聲歸并處理造成的誤差。本文中所采用的融合算法，僅利用數據自身蘊含的信息建立支持度函數，不必預設界限值以確定支持區間，避免了人為干預數據的主觀性，使預測值精確度更高。與常規GM(1,1)模型相比，本文預測結果誤差更小，精度更高，可更準確地反映實際情況。

3 結 論

1）本文采取的融合算法在對碼頭位移觀測值進行預測過程中，利用初始數據之間的差值計算元素之間的支持度，并以此為基礎構建權重矩陣，可充分挖掘數據的原始信息，不必預先設定界限值，降低處理數據的主觀性，提高預測精度。

2）與常規GM(1,1)模型相比，本文采用的預測模型可充分利用數據間的冗余和互補信息，消除實測數據中存在的噪聲影響，更好的反應真實情況，具有更高的預測精度，其預測結果可以作為碼頭安全監測的相關依據，具有良好的應用價值。