機翼極限環顫振的CFD/CSD全隱式緊耦合方法*

黃 杰， 姚衛星,2， 姜志平， 周丹發

(1. 南京航空航天大學機械結構力學及控制國家重點實驗室 南京，210016)(2. 南京航空航天大學飛行器先進設計技術國防重點學科實驗室 南京，210016)(3. 中國航空工業集團公司沈陽飛機設計研究所 沈陽，110035)

引 言

氣動彈性是飛行器設計過程中必須考慮的問題，相比靜氣動彈性，顫振對飛行器帶來的危害更嚴重，若設計不當，飛行動壓達到顫振臨界動壓時，飛行器將發生機毀人亡的事故。早期的飛行器顫振分析基于經典顫振理論，典型的分析方法有v-g法和p-k法[1-2]。經典顫振理論為頻域分析方法，非定常氣動力的分析通常采用偶極子網格法[3-4]，該氣動力模型為線性模型，只適用于亞聲速和超聲速問題，無法分析高度非線性的跨聲速問題。當攻角較大時，流動分離也會導致氣動力非線性，故偶極子網格法也無法分析大攻角問題。經典顫振理論的結構動力學通常采用模態疊加法分析，同樣也為線性模型。因此，經典顫振理論僅能分析亞聲速或超聲速、小攻角、線性結構等條件下的顫振問題。

對于大型客機和高速無人機，巡航速度大多處于跨聲速區域，其氣動力是高度非線性的。而大展弦比無人機機翼柔度較大，在氣動力作用下會產生較大的幾何變形，機翼必然會產生明顯的幾何非線性效應，而幾何非線性會造成翼面結構在非定常氣動力作用下發生極限環振蕩(limit cycle oscillation,簡稱LCO)[5-6]，同時發生顫振問題和LCO現象時可稱為極限環顫振[7-9]。LCO顫振分析的關鍵是準確計算LCO幅值和頻率。因此，經典顫振理論無法分析這類高度非線性的LCO顫振問題。隨著計算流體力學(computation fluid dynamics,簡稱CFD)和計算結構動力學(computational structural dynamics,簡稱CSD)的發展，一些學者開始采用基于CFD/CSD的耦合方法進行LCO顫振的研究，非定常氣動力通過有限體積法求解Euler方程或Navier-Stokes方程獲得，而結構瞬態響應分析通常采用非線性有限元法，因此這是一種時域方法。目前LCO顫振的研究對象主要集中在壁板，而機翼的LCO顫振研究相對較少。Schairer等[10]通過試驗方法研究了切尖三角翼的LCO顫振問題，獲得了三角翼的模態及不同來流動壓下的翼尖LCO幅值和LCO頻率。文獻[11-13]通過CFD/CSD耦合方法研究了切尖三角翼的LCO顫振，并將計算結果與試驗結果進行了對比。該耦合方法具有松耦合的特點，耦合時間精度較低，具有時間滯后效應，已有學者證明了松耦合方法僅具有一階耦合時間精度[14]。

針對松耦合方法的時間滯后效應及耦合時間精度較低的缺點，筆者發展了一種跨聲速翼面極限環顫振的CFD/CSD緊耦合分析方法，其特點是在傳統松耦合方法的基礎上增加了內部偽迭代分析過程。采用Schairer等的試驗模型進行了緊耦合和松耦合分析，并將計算結果和試驗結果進行了對比，以驗證緊耦合方法的耦合時間精度。

1 氣動力和結構動力學控制方程

不考慮體積力和內熱源情況下，直角坐標系下的流體動力學Navier-Stokes控制方程的積分形式為

(1)

其中：W為守恒向量；Fc為對流通量；Fv為黏性通量；?V為控制體V的邊界面；n為?V的外法線單位向量。

(2)

(3)

(4)

(5)

其中：ρ為密度；p為壓強；u，v和w分別為直角坐標系下的速度分量；qx，qy和qz分別為直角坐標系下的熱流分量；e為單位質量氣體的總能量，其表達式為p/((γ-1)ρ)+(u2+v2+w2)/2；γ為氣體比熱比；τij為黏性應力分量。

將式(1)按有限體積法進行空間離散可得

(6)

其中：Wi和Vi分別為控制體i的守恒向量和體積；NF為控制體邊界面的數目；ΔSN為第N個邊界面的面積。

由于對流通量Fc具有高度非線性特點，并且集中體現了流場的對流特征，筆者采用Roe格式[15]對其進行空間離散，為獲得單調解，采用完全迎風的二階MUSCL格式[16]離散分裂后的無黏通量,并采用minmod限制器使空間離散格式達到空間二階精度，且非定常問題的求解采用雙時間步長法[17]。

以上是氣動力分析的控制方程和數值計算方法，而通過有限元法離散后結構動力學運動方程可表示為

(7)

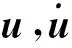
本研究的機翼極限環非線性顫振僅考慮結構的幾何非線性，不考慮其材料非線性，且采用Newmark法進行結構非線性瞬態動力學的求解，其屬于隱式求解方法。將式(7)寫為結構非線性動力學的平衡方程為

(8)

Fi體現了結構的幾何非線性，需要將其線性化以方便求解

Fi,n+1=Fi,n+KT,nΔu

(9)

其中：Δu=un+1-un。

將式(9)帶入式(8)，即可得到線性化的結構動力學的平衡方程

(10)

由于式(9)在一定程度上屬于一階線性化，故一階線性化的式(10)求解精度較差，可引入子迭代Newmark方法來求解式(10)，其平衡方程為

(11)

基于子迭代Newmark方法的結構瞬態非線性動力學求解的詳細過程可參考文獻[14]。

2 全隱式緊耦合分析策略

本研究非定常氣動力采用CFD方法求解，而結構非線性動力學采用基于有限元的CSD方法求解，且CFD和CSD均采用隱式時間推進，相比顯示格式，隱式格式能采用更大的時間步長且具有更好的穩定性。

傳統的機翼非線性顫振分析采用基于CFD/CSD的串行松耦合方法，其在相同的時間步進行氣動力和節點位移的數據交換，并進行迭代推進求解。松耦合方法簡單明了，實現起來較容易，但在任意n到n+1時間步內CFD(或CSD)求解過程中節點位移(或氣動力)不變，即凍結邊界條件，這樣會造成時間滯后的效應，且隨著分析的進行，累積誤差會越來越大。文獻[14]已經證明了即使CFD和CSD分析均達到了二階時間精度，由于耦合邊界上氣動力和節點位移在交換時間上的滯后，傳統松耦合方法只能達到一階時間精度。這明顯不滿足機翼極限環顫振對耦合方法時間精度的要求。

基于傳統松耦合方法時間精度較低的缺點，筆者采用全隱式緊耦合方法進行機翼極限環顫振的研究。其在任意一個時間步內CFD與CSD進行反復的內迭代，通常將其稱之為偽迭代。當流體與結構滿足精度要求，跳出偽迭代進行下一個時間步的求解，即進入物理迭代的分析。相比松耦合方法，緊耦合方法增加了偽迭代，并要求偽迭代收斂后才進行物理迭代的計算，這在一定程度上能消除松耦合方法在時間推進過程中累積的誤差，即降低松耦合方法存在的時間滯后效應，具有更高的耦合時間分析精度。由于偽迭代完全收斂后再進入物理迭代，造成了計算量大大增加。因此在實際的緊耦合分析中通常需要設置一個最大偽迭代次數，即當偽迭代達到最大次數時即使其還未完全收斂，也跳出偽迭代進入物理迭代。

如圖1所示，緊耦合方法的主要分析步驟如下：

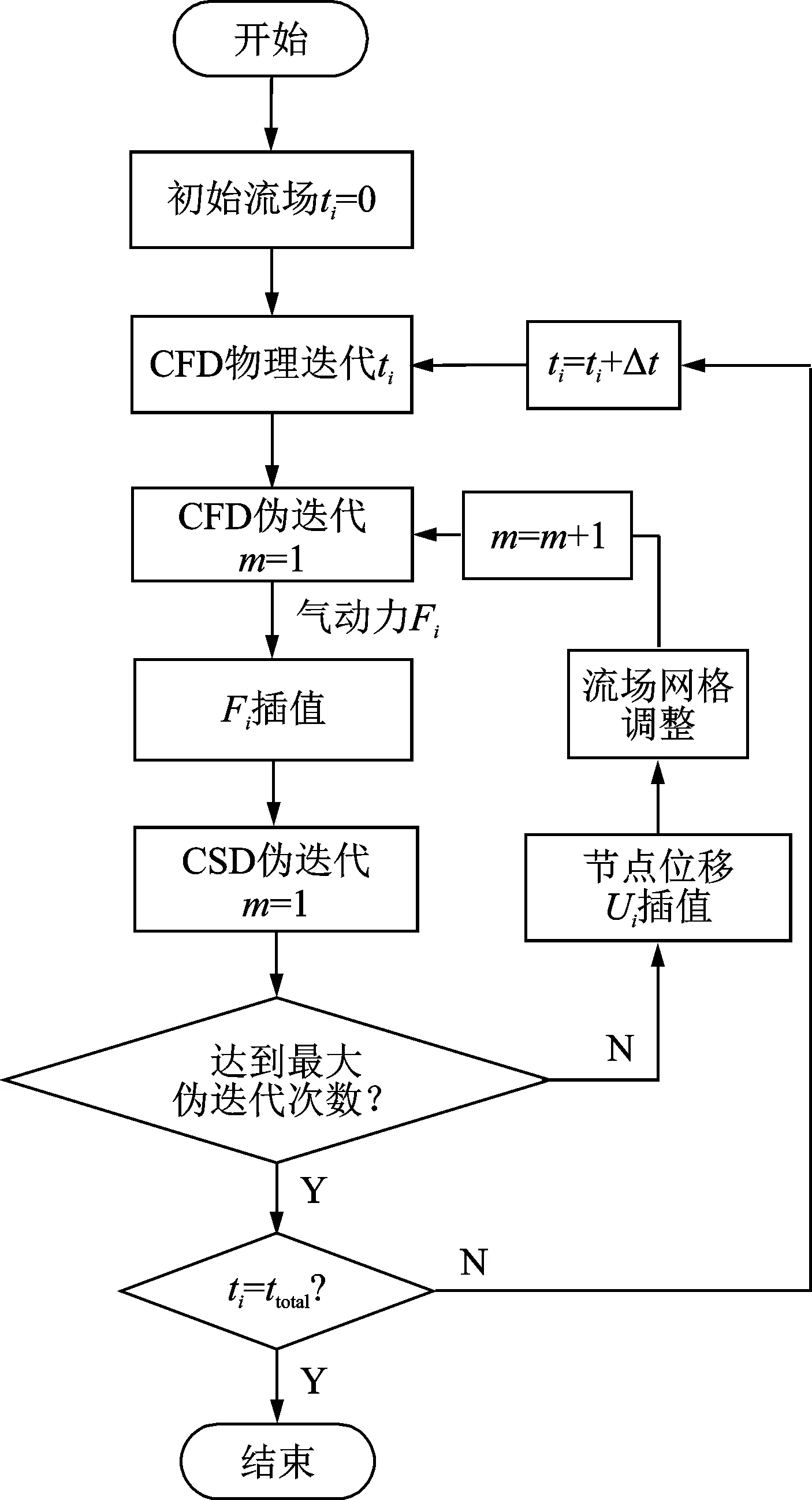
圖1 緊耦合方法分析流程Fig.1 Analysis process of tightly coupled method

1) 進行CFD和CSD建模，并進行CFD定常流場的計算，計算得到的定常氣動力結果作為耦合分析的初始條件；

2) 進行ti時刻的非定常氣動力的計算，并將壁面壓力熱Fi傳遞給CSD模型，進行CFD與CSD的偽迭代分析，直到偽迭代達到最大迭代次數后結束該時間步內的偽迭代分析；

3) 進行下一個時間步的分析，即進入物理迭代的計算；

4) 若物理迭代分析時間ti到達分析總時間ttotal，結束分析，否者返回步驟2，直至ti=ttotal為止。

以上耦合流程中涉及到氣動力和節點位移在耦合面上的數據交換，而CSD的網格尺寸通常遠大于CFD網格尺寸，故在耦合面上不能直接通過節點一一對應的方式進行以上耦合變量的傳遞，需要采用插值算法完成數據的傳遞。筆者采用三維薄板樣條插值方法進行氣動力和節點位移的插值計算。此外，結構變形會導致流場網格的重新調整，筆者采用基于無限插值方法的動網格技術實現流體網格的變形，其詳細計算方法可參考文獻[18]。

3 跨聲速切尖三角翼極限環顫振分析

3.1 數值模型

筆者采用跨聲速切尖三角翼試驗模型[11]進行研究，通過試驗可知，該模型的非線性因素來自于氣動載荷作用下的結構大變形和跨聲速非線性氣動力。此剪切三角翼為等厚度薄板，其厚度為0.889mm，材料為鋼，彈性模量為200GPa，泊松比為0.25，密度為7 850kg/m3，其平面形狀和幾何尺寸如圖2(a)所示，且翼根為固支邊界條件。來流馬赫數在0.86和0.879之間，攻角為0°。為了與試驗來流參數相匹配，來流動壓的單位采用psi，其與Pa的變換關系為1psi=6 895Pa。圖2為CFD和CSD數值模型，由于采用松耦合方法分析該模型極限環顫振的文獻中未考慮流場的黏性效應，為了對比分析，本研究CFD模型僅求解Euler方程。此外CSD模型采用殼單元模擬，且考慮結構大變形帶來的幾何非線性效應。

圖2 流體和結構模型網格Fig.2 Fluid and structural meshes

筆者進行了結構模態分析，結構振型的試驗和分析結果如圖3所示，機翼前3階振型分別為一階彎曲、一階扭轉和二階彎曲，且分析結果與試驗結果吻合得很好。表1列出了機翼前3階固有頻率的試驗和分析結果[11]，固有頻率的計算值與試驗值最大相對誤差為1.82%，這說明本研究的CSD模型能夠反映切尖三角翼的基本動力學性能。

圖3 機翼振型對比Fig.3 Comparison of modal shape of wing

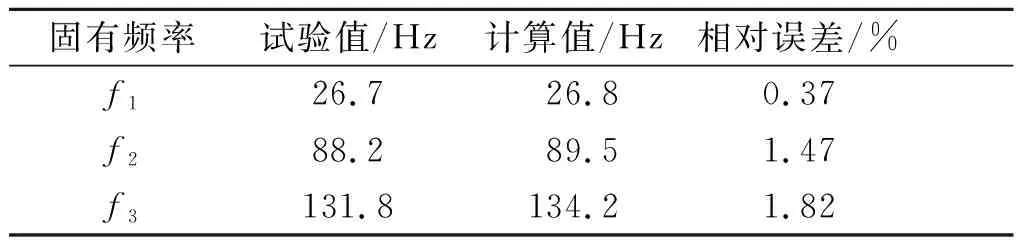
表1 機翼固有頻率的對比

3.2 機翼幾何非線性的影響

為了研究結構幾何非線性對顫振的影響，筆者采用緊耦合方法同時分析了來流動壓q=2.58psi下考慮和不考慮幾何非線性時的翼尖瞬態位移響應，其中耦合時間步長Δt取0.000 4s，每個時間步內的最大為迭代為10。圖4為線性結構(不考慮結構幾何非線性)和非線性結構下的結果對比圖，可知考慮結構幾何非線性時機翼在初始擾動下振動幅度逐漸增加，并且在最終呈等幅振蕩狀態。這是因為翼面為剛度漸硬的系統，即隨著翼面變形的增加，翼面幾何剛度也逐漸增加，機翼抵抗變形的能力得到了加強。線性剛度的機翼在分析過程中剛度保持不變，當受初始擾動時，機翼在初期呈現較小幅度的振動，隨后進入劇烈的動態發散階段，此階段機翼的變形遠大于考慮幾何非線性情況下的結果。據此可知機翼幾何非線性對時域分析結果產生了重要影響，必須考慮其影響才能獲得正確的顫振分析結果。

圖4 翼尖線性和非線性位移響應(動壓q=2.58psi)Fig.4 Linear and nonlinear displacement responses of wing tip(q=2.58psi)

3.3 非線性臨界顫振動壓

筆者采用緊耦合方法進行了切尖三角翼的臨界顫振動壓分析，同時考慮了非線性跨聲速氣動力和結構幾何非線性。圖5為不同動壓下機翼翼尖的法向位移時域分析結果，根據結果可知：動壓q為2.42psi時，在外界擾動下翼尖的振動呈收斂的趨勢；動壓q為2.44psi時，翼尖的振動逐漸發散；動壓q為2.43psi時，翼尖呈近似等幅振動的狀態，故本研究的切尖三角翼模型非線性臨界顫振動壓為2.43psi。

圖5 不同動壓下翼尖位移響應Fig.5 Displacement responses of wing tip under different dynamic pressure

表2為p-k法[13]與本研究緊耦合方法計算得到的臨界顫振動壓與試驗結果的對比情況，可知緊耦合方法獲得的臨界顫振動壓值2.43psi與試驗值2.40psi吻合良好，而p-k法計算得到的臨界顫振動壓為2.75psi，結果較差。這是因為p-k法為工程算法，其氣動力和結構分析均為線性，無法考慮切尖三角翼的非線性跨聲速氣動力和結構幾何非線性。表2中的數據同樣也驗證了緊耦合方法在求解非線性臨界顫振動壓中的高精度。

表2 非線性顫振動壓比較

3.4 LCO分析結果和討論

在切尖三角翼的顫振試驗中觀察到了LCO現象，其中的非線性來自于非線性跨聲速氣動力和結構幾何非線性，且結構幾何非線性是主要影響因素。筆者分析了不同來流動壓下的翼尖法向位移的時域結果和相應的相位圖，如圖6所示。從圖中結構可知，在初始擾動下翼尖振動在初始階段呈現輕微的發散趨勢，隨后翼尖振動進入劇烈發散階段，翼尖位

圖6 不同動壓下翼尖位移響應及相位圖Fig.6 Displacement responses and phase diagrams of wing tip under different dynamic pressure

移迅速增加，并且最終作等幅振蕩的狀態，即表現出LCO現象。此外隨著來流動壓的增加，翼尖會更劇烈且更快地進入LCO狀態。

分析獲得了不同來流動壓下的翼尖LCO幅值和頻率，如圖7所示，圖7(a)中的縱坐標為LCD與機翼半展長b(其值為203.2mm)之比。為了對比分析，圖中還給出了一些采用松耦合方法獲得的結果。為了保證對比分析的合理性，本研究緊耦合方法和文獻中松耦合方法的氣動力分析控制方程均為Euler方程，且耦合時間步長均為0.000 4s。由圖可知，緊耦合和松耦合方法獲得的LCO幅值在較低來流動壓下吻合較好，隨著來流動壓的增加，計算值與試驗值誤差越來越大，尤其在來流動壓q=3.45psi時LCO幅值的試驗值遠大于所有計算值，但可以明顯觀察到采用緊耦合方法獲得的LCO幅值更靠近試驗值。隨著來流動壓的增加，LCO頻率的試驗值逐漸增加，緊耦合方法計算得到的LCO頻率能清晰地反映這一規律，而松耦合方法卻不能。此外，緊耦合方法獲得的LCO頻率也與試驗值吻合得更好。

圖7 不同動壓下翼尖LCO幅值和頻率Fig.7 LCO amplitude and frequency of wing tip under different dynamic pressure

以上分析說明了緊耦合方法比傳統松耦合方法能更好地分析LCO幅值和頻率，具有更高的分析精度。但是在較高來流動壓下，緊耦合方法獲得的LCO幅值及頻率與試驗值還存在較大的誤差。主要原因有：①三角翼的扭轉變形會造成局部大攻角，三角翼在大攻角下會形成前緣分離渦和前緣低壓區，如圖8所示，這難以通過Euler方程進行數值模擬，即存在氣動力不精確的問題；②試驗過程中機翼的振動容易引起翼根的松動[11]，降低約束剛度，造成振動幅值增加；③翼根部為高應力區域，有部分結構已進入塑性階段，而本研究的分析不考慮材料非線性，這也將引起振幅增加。

圖8 翼面壓力系數分布Fig.8 Pressure coefficient distribution of wing

4 結 論

1) 傳統松耦合方法分析過程中存在嚴重的時間滯后問題，會影響耦合時間精度。筆者發展了一種機翼極限環顫振的CFD/CSD全隱式緊耦合研究方法，其特點是在傳統松耦合方法的基礎上增加了內部偽迭代分析過程。

2) 進行了切尖三角翼跨聲速極限環顫振的分析，結果表明結構幾何非線性對LCO顫振具有重要影響，且緊耦合方法獲得的機翼臨界顫振動壓與試驗結果吻合得很好，從而驗證了緊耦合方法的分析精度。

3) 緊耦合方法獲得的翼尖LCO幅值和LCO頻率均優于傳統松耦合方法，更靠近試驗結果，故緊耦合方法在一定程度上能消除時間推進累積的誤差，具有更高的耦合時間精度。

4) 本研究的緊耦合方法不僅能應用于機翼極限環顫振的分析，還可應用于對時間精度要求較高的機翼突風響應以及其他類型的瞬態耦合分析中，如氣動熱與結構傳熱的瞬態耦合分析，因此緊耦合方法具有廣泛地工程應用價值。