基于熱傳導模型的高溫作業專用服裝最優厚度設計

王哲 陳思 林可楓

摘要：對于高溫作業專用服裝最優厚度設計問題，通過建立相應熱傳導模型，使用有限差分方法得到溫度分布情況，并針對不同目標層數的優化問題，運用曲線擬合以及基于神經網絡的遺傳算法進行尋優求解。立足于實驗數據，合理利用MATLAB等軟件編程，得出在給定環境條件下高溫作業專用服裝的溫度分布及不同要求下的最優厚度。

關鍵詞：熱傳導定律;高溫作業專用服裝;有限差分;基于神經網絡的遺傳算法;MATLAB

中圖分類號：TB文獻標識碼：Adoi：10.19311/j.cnki.16723198.2020.25.076

高溫作業環境包括緊急滅火、工業冶金等高溫的危險環境，這極易對工作人員的人身安全構成威脅。工作人員需要在高溫環境中穿戴高溫作業專用服裝，保護自身不受火焰、蒸汽、易燃液體等傷害。隨著現代科學技術飛速發展，無論是工業生產還是高科技技術領域，工作人員在高溫作業環境中的需求越來越高，這就要求對高溫作業專用服裝需要進行更安全合理地設計。

目前高溫作業專用服裝的研究在國際上已是熱點問題。施無右對國內外高溫作業專用服裝的研究進行系統介紹，分析各類服裝的優缺點，為我國進一步研制高溫作業專用服裝提供參考。蘇云從服裝與人體之間空氣層出發，對空氣層的熱傳遞機制建立數學模型，在小平小尺度臺式實驗基礎上進行研究。王棋生從高溫作業服裝的相變材料分布出發，測試得出有效防護間隙分布，通過真人實驗經行驗證最終設計滿足作業環境要求的高溫作業專用服裝。以上研究不足之處在于僅設計了單層高溫作業防護服，但實際工作中是多層材料共同設計制作。基于目前研究，本文通過建立熱傳導模型求解得出各織物層及空氣層的溫度變化，并在已有實驗數據基礎上，設計在不同作業要求下高溫作業專用服裝的最優厚度。

1數據來源及假設

本文數據來源于2018年高教社杯全國大學生數學建模競賽A題，為了降低研發成本、縮短研發周期，對高溫作業專用服裝最優厚度進行優化求解。為更好地分析和解決問題，現提出以下假設：（1）假設防護服各層之間無縫隙。若防護服織物之間有縫隙，則會產生對流傳熱的現象，對實驗的計算產生影響。（2）假設不同情況下環境溫度與假人體內溫度恒定。若在研究某情況時，環境溫度與假人體內溫度變動，那么傳熱過程不會趨于穩態。（3）假設不考慮氣體對流及熱輻射現象。（4）假設熱傳遞沿垂直于皮膚方向進行。（5）假設數據來源準確可靠。（6）假設材料密度均勻，熱傳導系數不變。

2利用差分法對高溫作業專用服裝溫度分布求解

2.1研究思路

研究目的是在各織物層及空氣層已知的情況下，計算溫度分布。根據傳熱學的熱量守恒定律和傅里葉實驗定律，建立高溫作業專用服裝各層的熱傳遞模型。通過使用有限差分的方法來解決該系統偏微分方程，并利用已知假人皮膚外側溫度的數據，不斷改變未知量的取值來確定其最優值，最終即可得到最佳的模型解，該解即為在各織物層及空氣層厚度已知的情況下的溫度分布。

2.2模型建立

對于高溫環境-防護服-皮膚系統，由于織物層厚度較厚，且空氣層厚度值不超過6.4mm，所以不考慮熱輻射與氣體對流，其熱量傳遞的主要形式為熱傳導。又由假設知熱傳遞沿垂直于皮膚方向進行，所以可將該系統視為一維的問題。針對該系統問題，可得示意圖如圖1。

在三維空間中，要考察一給定物體D的熱傳導問題，首先設該物體上的點（x，y，z）在時刻t的溫度為T（x，y，z，t）。

根據傅里葉傳熱定律，在單位時間dt內，對于任意趨向無窮小的單位面積dS，流出該面積的熱量dQ沿其法線方向n與法線的方向導數T/n成正比，即：

其他織物層、空氣層、皮膚層及其邊界做相同的處理。

該模型中，時間的步長取Δt=0.01s，其它層距離的步長取Δx=0.0001m，空氣層的步長取Δx=00007m，根據相關文獻，可知人的皮膚組織的平均厚度為 0.5-4毫米，故假設假人的皮膚厚度為L

該模型的總體誤差為191.0909，平均誤差為0116，由此能夠看出該模型的擬合效果很好。

3設計第Ⅱ層最優厚度的單目標優化

3.1研究思路

本研究旨在找到環境溫度為65℃、第Ⅳ層的厚度為5.5mm時第Ⅱ層的最優厚度，在滿足工作條件要求下的時候希望高溫作業服的重量越輕越好，也就是越薄越好，使之既方便作業，也節省材料。因此可以通過建立以高溫作業專用服裝第Ⅱ層的最薄厚度為目標函數，研究中的工作條件要求為約束條件的單目標優化模型，并進行求解得到第Ⅱ層的最優厚度。

3.2模型建立

本研究仍使用如上建立的熱傳導模型，通過給定的條件確定新的定解條件來求解每一個位置在每一個時刻的溫度T（x，t），由于第Ⅱ層的厚度為變量LⅡ，因此這個時候的溫度是關于位置、時間以及第Ⅱ層的厚度的函數Tx，t，LⅡ。

設計要求得到第Ⅱ層的最優厚度，在滿足工作條件限制下希望高溫作業服的重量越輕越好，也就是越薄越好。因此以第Ⅱ層的最薄厚度為目標函數。又因為對高溫工作服也有一定的要求，即到了60分鐘的時候，假人皮膚外側溫度不超過47℃，以及到了55分鐘的時候，溫度不超過44℃。

由此建立以下單目標優化模型：

3.3模型求解

首先，在上一研究中所建立的數學模型的基礎上添加新的定解條件。

織物層的左邊界新條件為：

4利用基于神經網絡的遺傳算法求解Ⅱ層和Ⅳ層最優厚度

4.1研究思路

本研究旨在找到環境溫度為80℃下第Ⅱ層和第Ⅳ層的最優厚度，同樣在滿足工作條件要求下希望高溫作業專用服裝的重量越輕越好，越薄越好。因此可以通過建立以高溫作業專用服裝Ⅱ層和Ⅳ層的最薄厚度為目標函數，工作條件要求為約束條件的多目標優化模型，并通過基于神經網絡的遺傳算法解得最優解。

4.2模型建立

本研究是將上一研究中單個目標的尋優推廣到對兩個目標的尋優。通過給定的條件確定新的定解條件，從而求解每一個位置每一個時刻的溫度T（x，t）。此時的溫度是關于位置、時間以及Ⅱ、Ⅳ層的厚度的函數Tx，t，LⅡ，LⅣ。

為確定Ⅱ、Ⅳ層的最優厚度，在滿足工作條件要求下希望高溫作業服的重量越輕、體積越小越好。因此分別設Ⅱ層和Ⅳ層的最薄厚度為目標函數。此處對高溫作業服要求工作30分鐘時，假人皮膚外側溫度不超過47℃，且到了25分鐘時，假人皮膚外側溫度不超過44℃。

可建立以下多目標優化模型：

4.3模型求解

對于所建模型的求解，可取相同間隔不斷改變第Ⅱ層和第Ⅳ層的厚度，從而求得在這些厚度組合對應情況下的假人的皮膚外側溫度。通過使用BP神經網絡算法擬合第Ⅱ層和第Ⅳ層的厚度與溫度的關系，并用遺傳算法求得滿足約束條件的臨界條件，再用遺傳算法得到臨界條件中兩個厚度之和的最小值即可。具體求解過程如下。

4.3.1有限差分法求解

首先，通過選取相同間隔不斷改變第Ⅱ層和第Ⅳ層的厚度，代入探究溫度分布時建立的熱傳導模型，并根據對應的定界條件得到30分鐘和25分鐘假人皮膚溫度關于第Ⅱ層和第Ⅳ層的厚度關系。

4.3.2BP神經網絡算法擬合

通過BP神經網絡來擬合出30分鐘和25分鐘假人皮膚溫度關于第Ⅱ層和第Ⅳ層的厚度的關系。

（1）BP神經網絡基本原理。

神經網絡是經過模仿大腦處理信息的方式，具有多個神經元相互連接而成的網絡。BP神經網絡是一種前饋型神經網絡，輸入層神經元與中間層神經元發生信息傳遞時需要計算兩個神經元之間的權重。中間層或輸出層將處理過的信息作為該層神經元輸入。如果輸出層的輸出結果不是期望輸入，就根據誤差修正模型不斷修正網絡的權值和閾值，從而使BP神經網絡預測輸出不斷逼近期望輸出。

（2）訓練網絡樣本數據處理。

由于神經網絡訓練需要大量數據，所以已知的100組數據不能滿足訓練要求，因此從插值過后的數據中隨機選擇10000組數據，前9900組作為訓練數據，后100組數據作為檢驗數據集。為了使數據的輸入更穩定有效，輸入數據必須能夠體現全面的樣本特征。于是為了獲得更好的擬合效果，需要對輸入數據進行歸一化處理，以助于對不同特征的樣本進行計算和分析，本研究中使用如下公式進行歸一化處理：

（3）網絡初始化。

本研究輸入第Ⅱ、Ⅳ層的厚度組，所以輸入層節點有2個，需要的結果為第Ⅱ、Ⅳ層與其對應溫度的關系，因此建立2-N-N-1的BP神經網絡結構，如圖6。

（5）結果輸出。

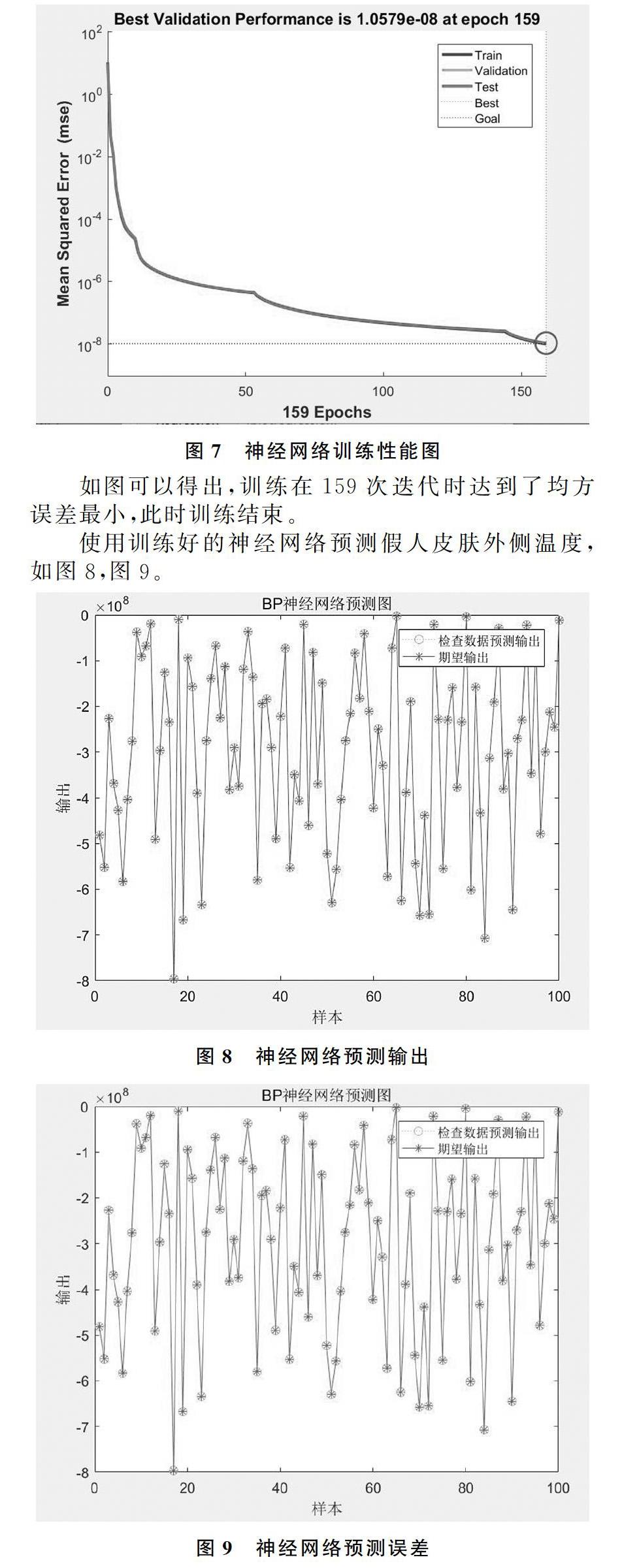
編程求解得到30分鐘和25分鐘假人皮膚溫度關于第Ⅱ層和第Ⅳ層的厚度關系，并用MATLAB將歸一化的數據進行反歸一化得到真實數據，訓練結束后的神經網絡性能圖如圖7。

通過以上圖像可以看出，預測輸出的結果與期望輸出相差不大，該模型的擬合效果良好。

4.3.3遺傳算法求解

為了滿足工作條件要求，可以使用遺傳算法求出臨界溫度所處的兩層織料厚度條件，然后在臨界條件再次使用遺傳算法求出兩層厚度和的最小值就即可得到兩層織料的最優厚度。

（1）遺傳算法概述。

遺傳算法是借鑒生物界的自然選擇和自然遺傳機制的一種計算算法，適用于機器學習、工程優化、人工智能、自適應控制等多個領域，并且大量應用于解決傳統優化算法難以解決的優化問題。其基本原理是模擬生物在自然環境中的優勝劣汰、適者生存的演化法則，將問題的參數編碼為染色體。把當初始種群確定之后，利用迭代的方式對種群進行選擇、交叉及變異等運算逐代演化，產生新的種群。這個過程使種群更加適應環境，最終生成符合優化目標的個體。

（2）初始化種群。

首先，對進行遺傳算法的種群初始化，確定對種群進行初始化的控制參數。由杜干的優化控制參數可得控制參數如表2。

（5）選擇、交叉、變異。

計算出每一個個體的適應度后，采用輪盤選擇法進行選擇，將選擇出的個體保留到下一代。在繁殖過程中兩個體對應的基因型會產生交叉，即對應位點的二進制編碼發生交換。依照突變規則，每個基因有0001的概率發生突變。突變時對應位點的二進制編碼會發生改變，即對應位點“0”與“1”發生變換。

（6）重復Step4、Step5，直到得到滿足誤差精度或者達到最大進化代數為止。此時得到的解即為第II層厚度最優解的二進制。通過將其解碼既得所求。

最終求得第Ⅱ層和第Ⅳ層的厚度的最優值為：

5結語

本文根據熱傳導定律，主要針對高溫環境-專業服-皮膚系統建立熱傳遞模型。對于熱傳導模型的偏微分求解問題使用有限差分的方法，列出各層模型的顯式迭代格式，從而將定邊界問題中的邊界條件離散化。該方法與傳統求解偏微分方程的方法相比，可以得到各離散節點的函數值。使用曲線擬合的方法對第Ⅱ層厚度的單目標函數求最優解，有效避免了線性函數擬合效果較差的問題。利用基于神經網絡的遺傳算法，確定Ⅱ層和Ⅳ層在滿足約束條件的情況下的最小厚度。該算法可以較全面的得到多目標優化問題的解集而不是一個全局最優解。在實際操作中，熱傳導過程中還應考慮熱輻射與熱對流組成的影響，減少誤差，提升模型準確性。

綜上所述，本文建立的熱傳遞模型，綜合考慮了不同熱傳遞層的情況，同時巧妙運用智能算法進行求解，具有極大的科學性和創新性。所以本文的模型可用于高溫工作環境下的工作服研究，例如消防服織物層與空氣層的熱傳遞機制的研究，鋼鐵鍛造工廠的防護服設計等與熱傳遞有關的問題。同時，該熱傳遞模型也適用于對復合高溫隔熱材料隔熱性的測試問題。進行優化控制參數后的遺傳算法及基于遺傳算法的多目標優化算法，可以應用于機器學習領域，解決人工智能的學習問題;又可應用工期-成本-質量等工程中的優化問題。

參考文獻

[1]施無右.高溫作業防護展望──介紹幾種防熱服及“室溫冰”[J].勞動保護，1981，（07）：25.

[2]蘇云，王云儀，李俊，等.消防服衣下空氣層熱傳遞機制研究進展[J].紡織學報，2016，37（01）：167172.

[3]王棋生.相變材料分布對相變調溫熱防護效果的影響分析[D].蘇州大學，2016.

[4]盧琳珍，徐定華，徐映紅，等.應用三層熱防護服熱傳遞改進模型的皮膚燒傷度預測[J].紡織學報，2018，39（01）：111118+125.

[5]徐建良，湯炳書.一維熱傳導方程的數值解[J].淮陰師范學院學報（自然科學版），2004，（03）：210214.

[6]閆英.彩超測定皮膚及皮下組織厚度在慢性下肢靜脈性水腫療效評價中的意義[C].中華中醫藥學會周圍血管病分會學術大會論文集（一）.中華中醫藥學會，2009：243245.

[7]周雄，梁金祿，譚茂波，等.遺傳算法優化神經網絡的重金屬污染源預測[J].欽州學院學報，2017，32（05）：3439.

[8]劉慧敏，王宏強，黎湘，等.基于RPROP算法目標識別的數據歸一化研究[J].現代雷達，2009，31（05）：5560.

[9]王嶸冰，徐紅艷，李波，等.BP神經網絡隱含層節點數確定方法研究[J].計算機技術與發展，2018，28（04）：3135.

[10]邊霞，米良.遺傳算法理論及其應用研究進展[J].計算機應用研究，2010，27（07）：24252429+2434.