利用多普勒測量確定嫦娥四號著陸器精密定軌

曹建峰，張 宇，陳 略，段建鋒，鞠 冰，李 勰

(1. 航天飛行動力學技術重點實驗室，北京100094；2. 北京航天飛行控制中心，北京100094)

0 引 言

月球自轉與公轉速度相當，該特性使得月球始終以固定的一面指向地球[1]。為了提升對月球背面的認知，歷史上多顆探測器開展了月球背面的遙感探測[2-4]。受限于測控能力，早期月球的著陸探測僅停留于月球的正面[5]。2018年5月21日，嫦娥四號中繼衛星成功發射，并于同年6月14日進入位于地月拉格朗日L2點的使命軌道，具備為月球背面的著陸探測提供數傳服務的能力[6]。嫦娥四號的科學探測目標包括：低頻射電天文觀測、月表淺層結構探測以及形貌與礦物組成探測等[7]。

軌道計算是月球探測任務及科學探測活動實施一項關鍵技術，多普勒測量在環月探測器的定軌計算中一直扮演著重要角色。20世紀70年代，Muller等[8]利用Lunar orbiter 1～5的S頻段多普勒測量數據進行月球重力場研究，發現了質量瘤分布。Lunar Prospector探測器的多普勒測量精度為0.2 mm/s(10 s積分周期)，2011年發射的GRAIL-A，其軌道計算也主要依賴于X頻段的多普勒數據，其測量精度為0.03 mm/s(10 s積分周期)[9]。

中國探月工程以地基USB/UXB(嫦娥一號、嫦娥二號，嫦娥四號中繼星采用S頻段，其余探測任務采用X頻段)，天文VLBI測量完成月球探測器的測軌工作[10-11]。受限于測量數據的精度，嫦娥一號任務的軌道計算主要使用國內測站USB測距與VLBI時延、時延率測量數據[12]，實現了環月階段優于50 m的軌道精度。在探月工程的系統建設中，VLBI技術取得了長足進步[13-14]。嫦娥二號任務中，開展了深空相位測量試驗，獲取了約0.1 mm/s測量精度的多普勒數據(30 s積分周期)[11]，為我國自主高精度多普勒測量奠定了基礎。嫦娥三號任務中，X頻段的雙差多普勒測量精度為0.2～0.4 mm/s(10 s積分周期)，三程多普勒測量精度大約為0.3～0.5 mm/s(10 s積分周期)[15]。

嫦娥四號著陸器采用X頻段測量體制，測軌系統延續USB與VLBI模式，得益于設備的改造，多普勒測量精度得到進一步提升。本文對嫦娥四號著陸器環月飛行階段的測軌數據進行處理，分析多普勒數據對軌道計算的貢獻。

1 嫦娥四號任務概況

2018年12月8日，嫦娥四號著陸器搭載長征三號乙(CZ-3B)運載火箭從西昌衛星發射中心發射，歷經發射段、地月轉移段、環月飛行段后，12月12日進入環月軌道，2019年1月3日在距離月表15 km處實施動力下降，進行軟著陸。

嫦娥四號著陸器延續了嫦娥三號姿控模式，通過姿控發動機噴氣維持姿態穩定。環月飛行階段，著陸器采用環月飛行姿態，其-Y軸與月球自轉軸夾角偏差為8°，+X軸與太陽方向矢量夾角大約6°。當姿態偏移超過設計閾值，姿控發動機進行噴氣調整姿態。雖然姿控發動機設計為力偶模式，實際工作狀態下仍會對著陸器產生一定的加速度，影響著陸器的飛行軌跡。此外，著陸器還需要判斷是否需要姿態調整轉動角以滿足測控要求，即對日定向偏置，該動作也會對著陸器產生作用力。嫦娥三號的分析表明，環月飛行階段，姿控噴氣對1天的軌道預報精度影響大約為50 m[16]，因而任務實施期間并不考慮姿控噴氣對軌道計算與預報影響。

嫦娥四號著陸器攜帶有X頻段應答機，地基UXB設備跟蹤著陸器獲取觀測數據包括測距與測速(1 s積分周期)數據，中國VLBI網參與著陸器的跟蹤，準實時提供時延與時延率觀測數據。

2 多普勒觀測模型

為了滿足高精度多普勒數據的應用需求，軌道計算軟件中的多普勒建模采用基于泰勒展開的算法，使用月球、著陸器的速度與加速度信息，有效降低字長截斷誤差、行星星歷表插值誤差對多普勒建模精度的影響[17]。算法本質是對積分開始與積分末端的信號傳播距離的差分計算進行了改進。信號傳播距離的計算公式為，

(1)

(2)

式中：l表示信號的傳播距離，下標s,e分別表示積分開始與積分結束，rE表示質心天球參考系中的信號收(發)時刻地球的位置矢量，rsta表示測站的天球參考系位置矢量，rM表示信號轉發時刻月球的位置矢量，rsc表示探測器在月心天球參考系中的位置矢量，傳播距離的計算需要進行光行時迭代。

(3)

式中:x,y,z為r的坐標分量，Δx,Δy,Δz為Δr的坐標分量。則積分結束與積分開始的信號傳播距離差分可以表示為:

(4)

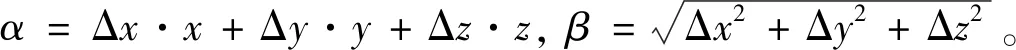
為避免計算精度損失，式中ΔrE與ΔrM使用質心天球參考系中地球與中心天體的速度計算，

(5)

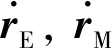
3 基于多普勒測量的軌道計算

為分析多普勒數據的獨立定軌能力，僅選用嫦娥四號環月階段的多普勒數據進行軌道解算。定軌計算中，為便于殘差統計與軌道比較，定軌弧段選取為每日0時至次日4時，共計28 h數據。在環月飛行階段，嫦娥四號除了常規的姿控噴氣外，還進行了多次的對日定向偏置，以及軌道控制。因此，28 h的定軌弧段內如果發生了軌道機動或是對日定向偏置之類的間斷力，則對該過程產生的加速度進行解算。定軌計算中采用勻加速度模型對此類間斷力進行建模，假定該作用力對探測器產生的加速度在軌道坐標系中恒定。表1給出了定軌計算所使用的基本策略。

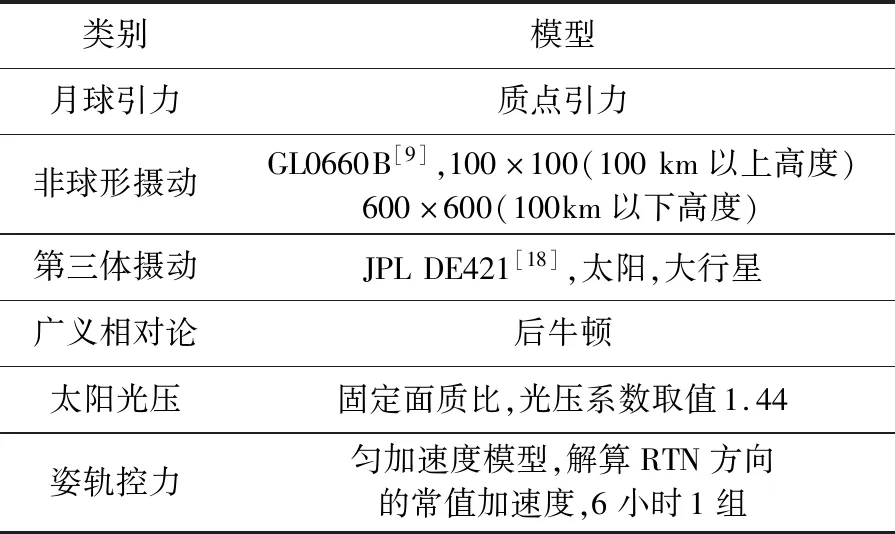
表1 定軌計算策略Table 1 Orbit Determination Strategy

3.1 定軌殘差統計

中國深空網的3個測站參與跟蹤嫦娥四號著陸器，其中佳木斯天線口徑為66 m，喀什35 m以及南美35 m天線[19]。對3個測站每天多普勒數據的定軌殘差進行統計，圖1給出了每個深空站多普勒數據定軌殘差RMS每日統計值。

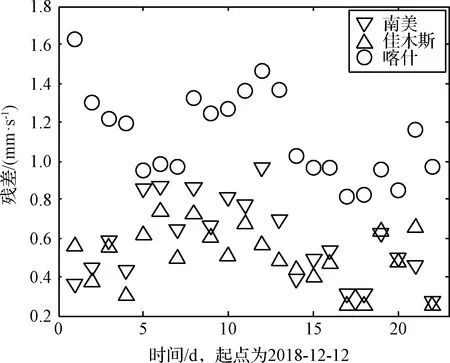
圖1 深空站多普勒數據殘差RMS統計Fig.1 RMS of DSN doppler residuals

3.2 重疊弧段軌道比較

選取每日1時至3時共計2 h的重疊弧段進行軌道精度比較，以降低邊值效應產生的影響。圖2給出了環月階段每天定軌星歷的重疊弧段比較。12月30日著陸器實施降軌控制，由100 km圓軌道降低至100 km×15 km軌道，期間還有頻繁對日定向偏置，因而這兩天的重疊弧段軌道比較結果稍差，但優于50 m，其余階段的重疊弧段總體偏差小于35 m，軌道偏差小于20 m的有10個重疊弧段。

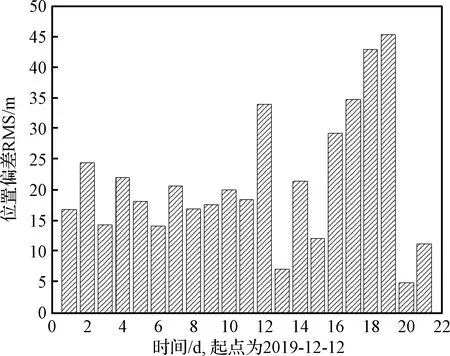
圖2 多普勒解算軌道重疊弧段比較精度統計Fig.2 Overlap comparison of doppler-only orbits

3.3 考慮姿控噴氣的軌道計算

著陸器依靠姿控發動機噴氣維持姿態穩定，所產生的作用力并非嚴格力偶，對質心產生一個細微加速度。對于頻繁姿控噴氣的飛行階段，該作用力會對軌道產生影響，若在定軌計算中完全忽略姿控噴氣的影響，會導致測軌數據的擬合較差，殘差呈現與軌道周期相一致的周期性。為了降低該作用力對軌道計算的影響，定軌計算中對頻繁姿控的弧段進行加速度估計，姿控力建模采用勻加速度模型，每6 h 解算一組軌道坐標系的常值加速度。

選取12月28日至29日(100 km軌道高度)連續2 d的數據進行分析，這2個弧段內著陸器未實施對日定向偏置，但姿控噴氣持續發生，軌道相對穩定。圖3～圖4給出了2 d定軌計算殘差圖，(a)部分為未進行姿控力解算，殘差存在明顯的周期項，(b)部分為解算姿控力后的殘差。通過姿控力的解算，數據殘差的周期性得到顯著抑制，噪聲水平大幅降低。

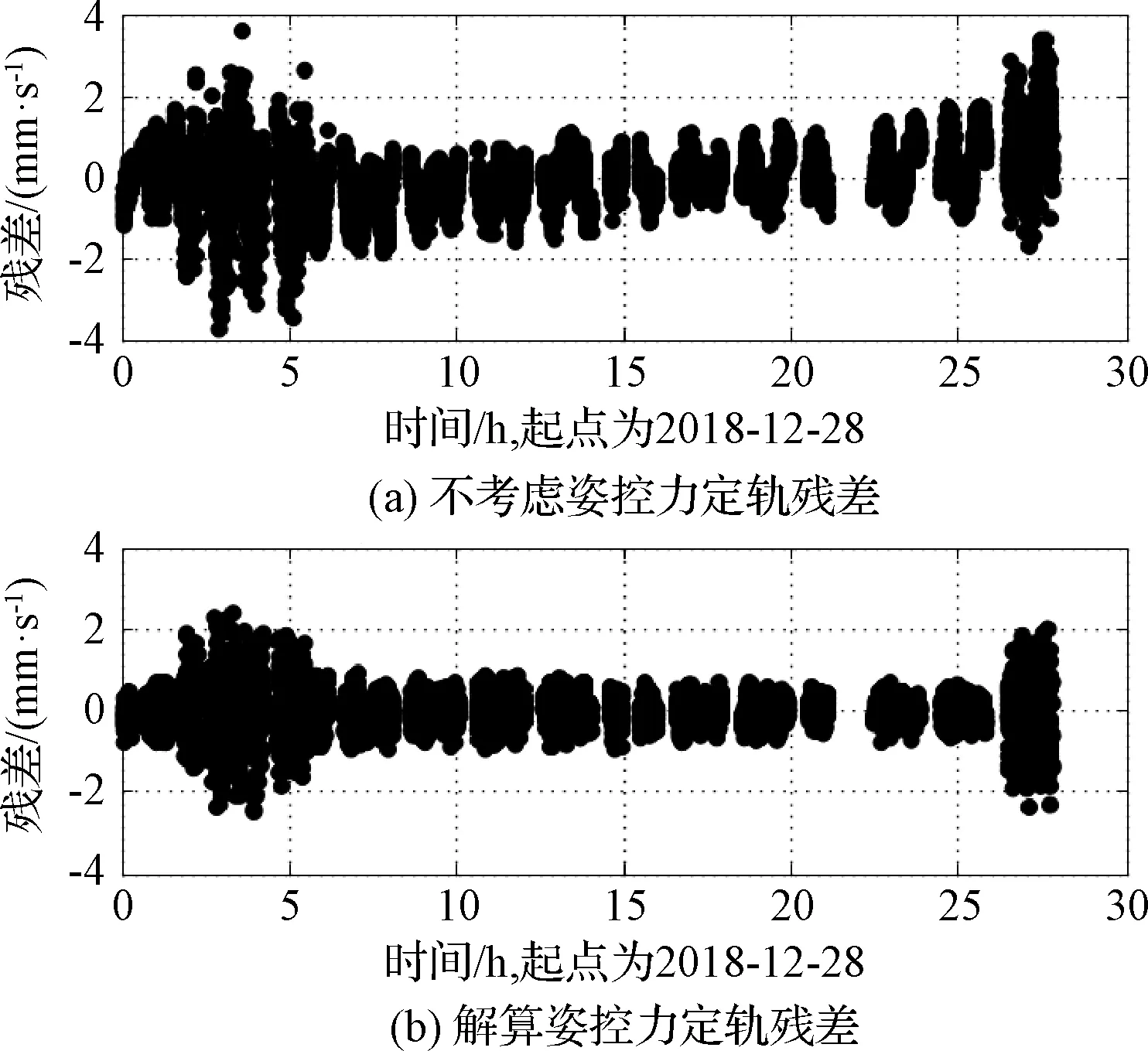
圖3 12月28日多普勒數據定軌殘差Fig.3 Postfit doppler residuals on December 28

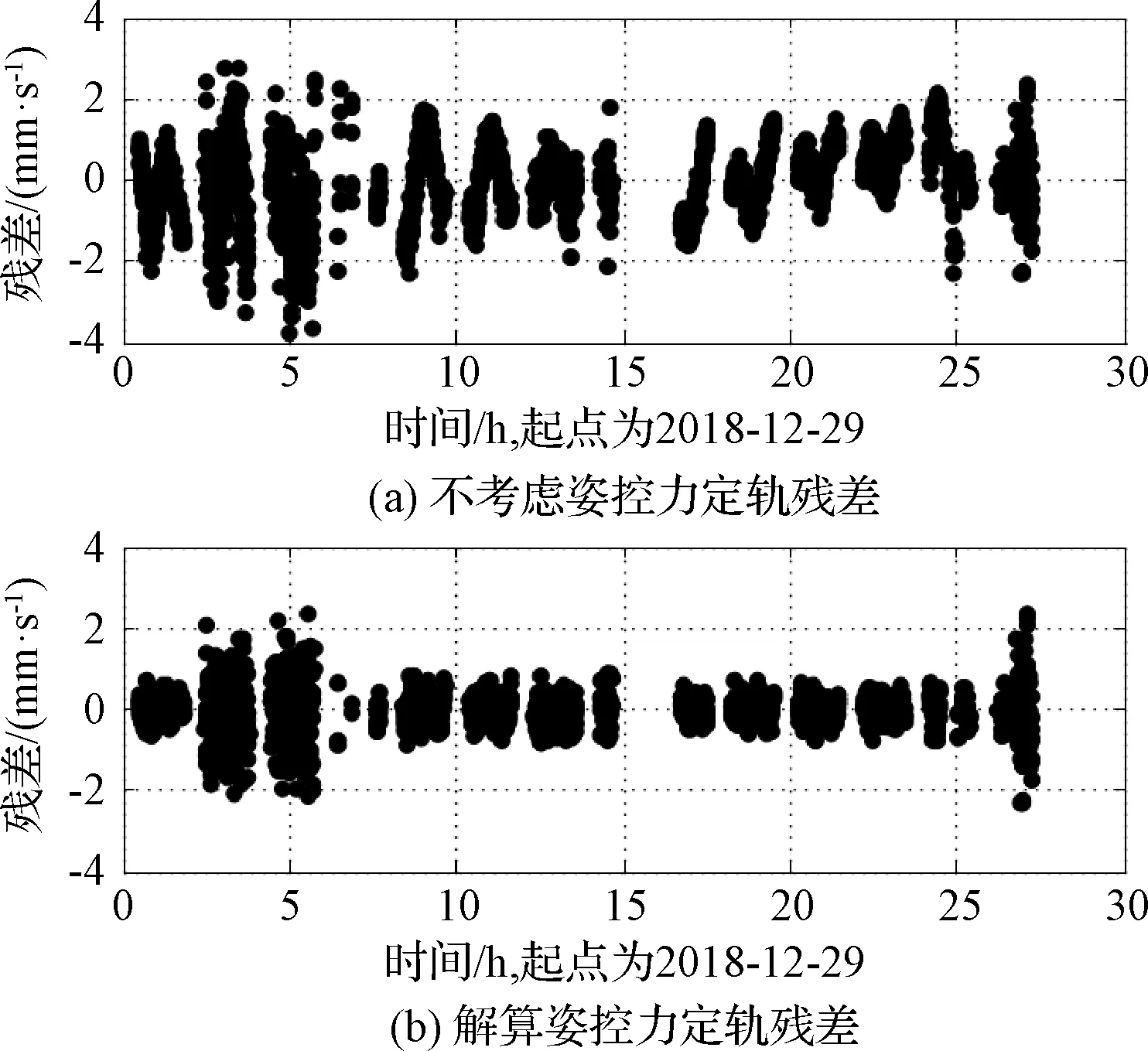
圖4 12月29日多普勒數據定軌殘差Fig.4 Postfit doppler residuals on December 29

對100 km×15 km軌道高度的軌道，選取2019年1月1日與2日兩天的數據分別進行分析，圖4～圖5為殘差分布。通過姿控噴氣力的解算，1月1日南美與佳木斯測站數據殘差的RMS降低1倍，喀什站數據殘差的RMS由0.99 mm/s降低至0.87 mm/s。1月2日，南美與佳木斯多普勒數據殘差RMS降低1倍，喀什數據RMS由2.0 mm/s降低至1.2 mm/s。與100 km×15 km高度軌道相比，100 km×15 km階段姿控噴氣更為頻繁，高階重力場的不準確對軌道的影響也更為顯著，因而姿控力的解算可以得到更為明顯的殘差擬合結果。

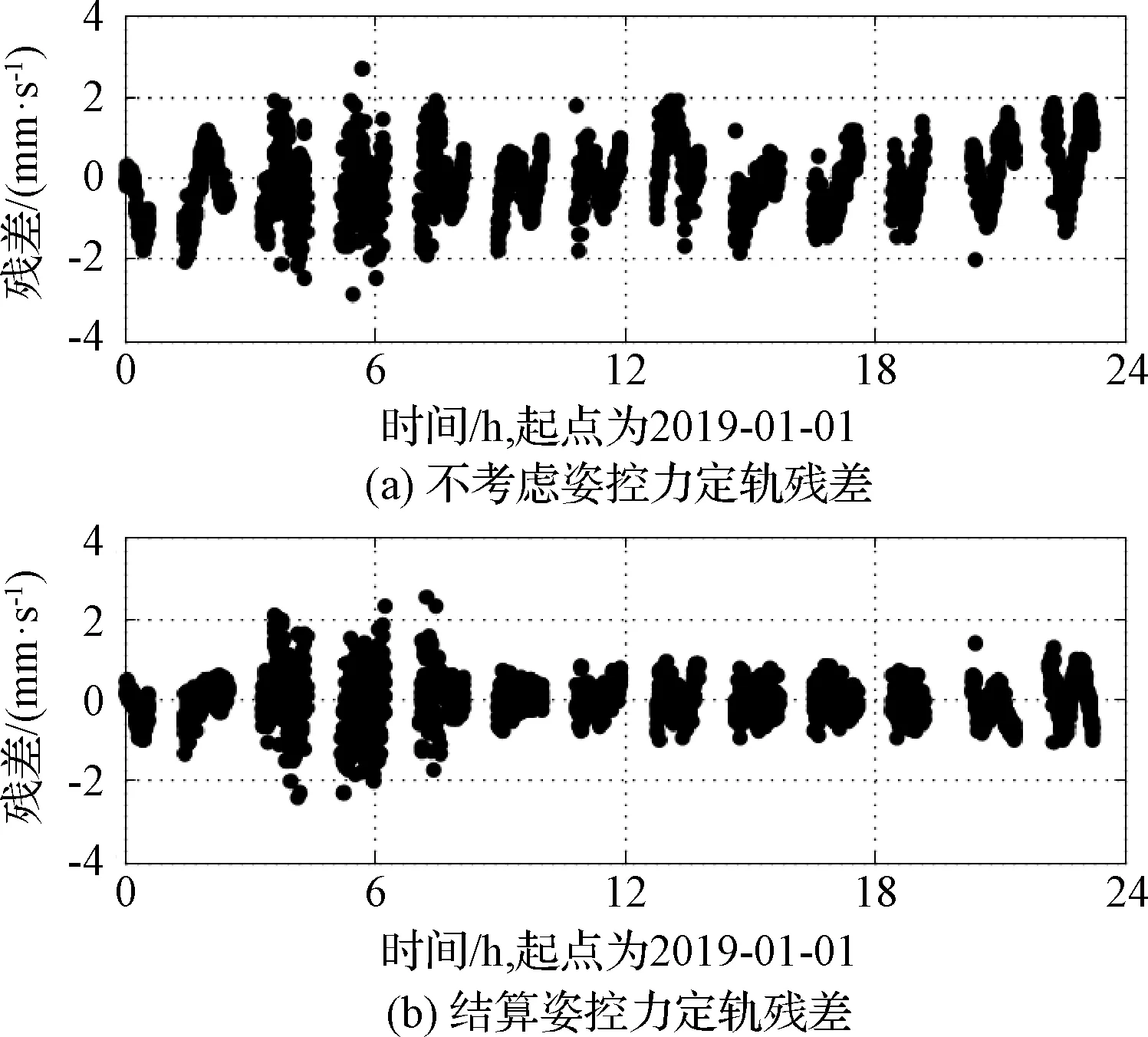
圖5 1月1日多普勒數據定軌殘差Fig.5 Postfit doppler residuals on January 1

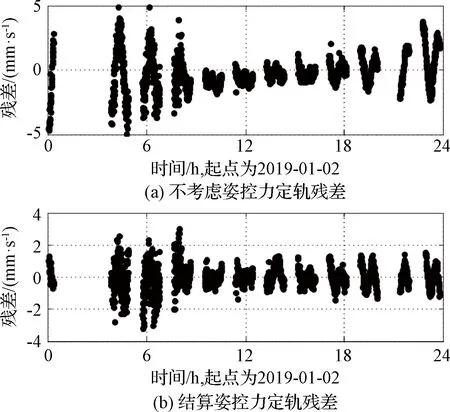
圖6 1月2日多普勒數據定軌殘差Fig.6 Postfit doppler residuals on January 2

以解算姿控力的軌道為基準，不解算姿控力的軌道作為比較軌道，分析姿控力解算對軌道計算的影響。100 km高度軌道，2組策略解算軌道的差異小于20 m；100 km×15 km軌道，2組策略解算軌道的差異小于50 m(如圖7～圖10所示)。對100 km×15 km軌道，軌道的偏差與姿控力解算的分段存在相關性。比較2組策略解算軌道的協方差，解算姿控力后的數據殘差雖然變小，但是解算軌道協方差并沒有顯著降低，甚至變大。如1月2日(如圖10所示)，不解算姿控力的軌道形式誤差為7.2 m，解算姿控力后的軌道形式誤差為13.1 m，姿控力的解算可能會增大軌道參數的協方差，即可能得到更差的解算軌道。

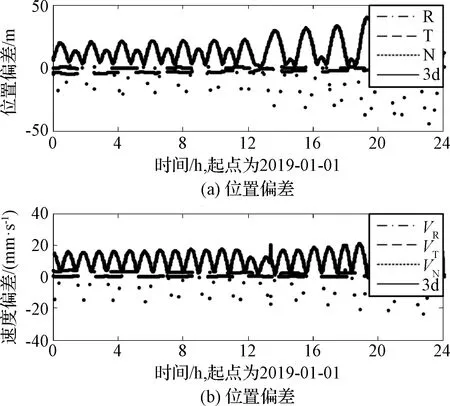
圖9 1月1日解算軌道比較Fig.9 Orbit solution comparison on January 1

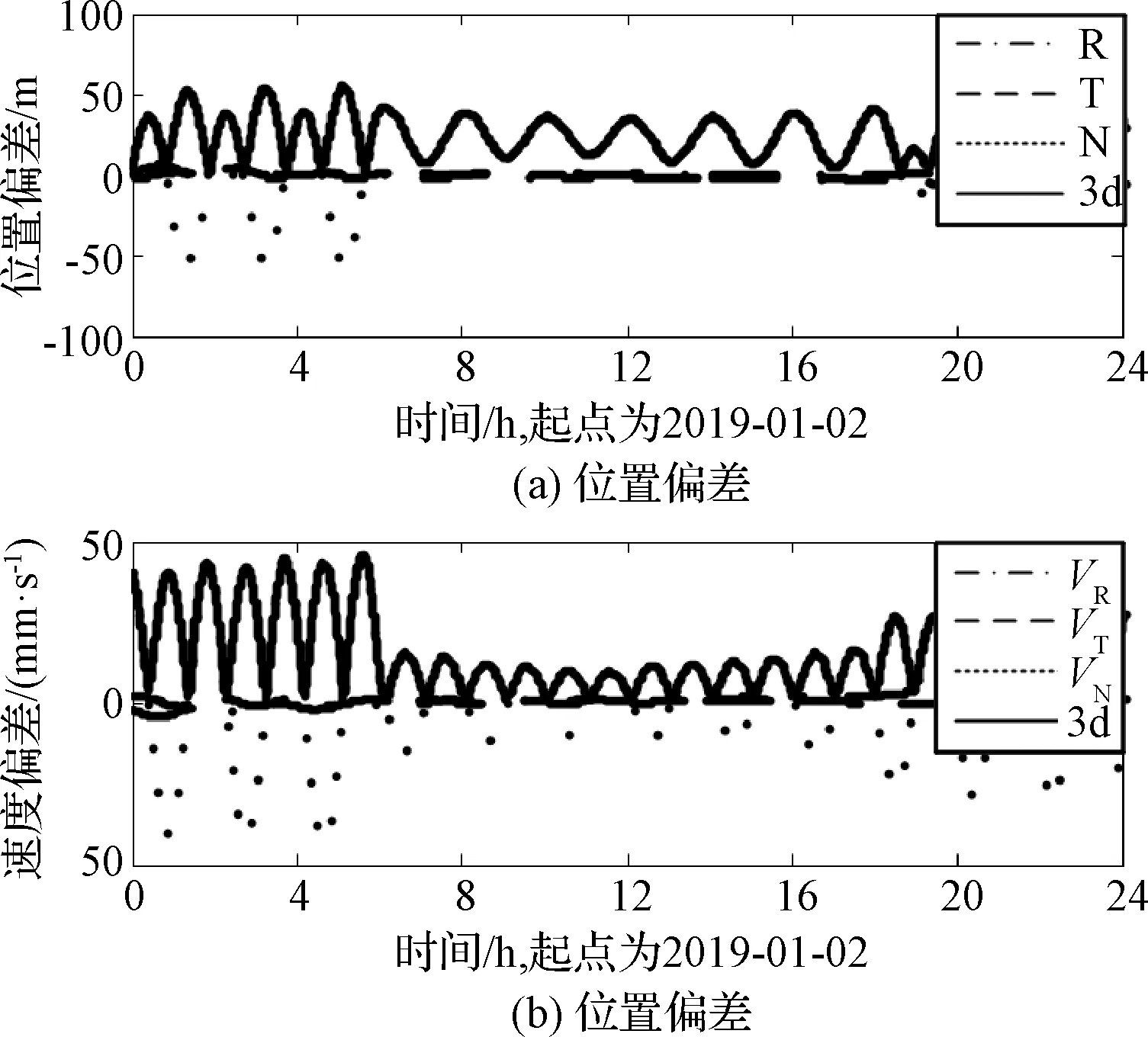
圖10 1月2日解算軌道比較Fig.10 Orbit solution comparison on January 2

4 基于測距+VLBI解算軌道的比較

本節對環月階段不同高度的軌道分別進行定軌計算，以基于測距和VLBI數據的解算軌道作為基準，檢驗多普勒數據獨立定軌的精度。

測距與VLBI聯合解算的軌道精度在歷次月球探測任務中得到了驗證，其精度可以穩定在10～50 m，圖11給出了使用USB測距與VLBI數據計算軌道的重疊弧段比較，定軌策略如表1所示。

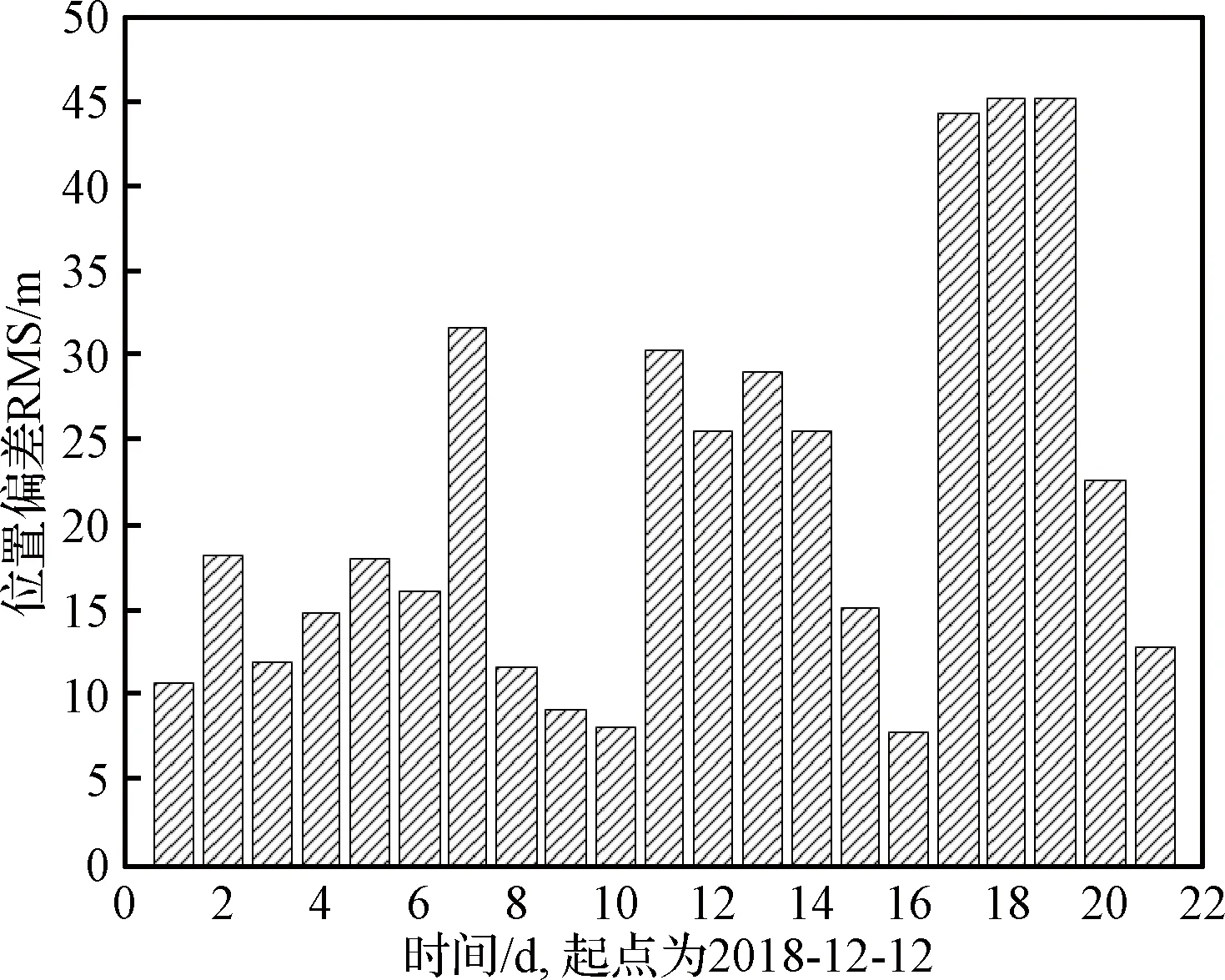
圖11 基于測距與VLBI解算軌道的重疊弧段比較Fig.11 Overlap comparison of ranging+VLBI orbits

以測距與VLBI解算的軌道作為基準，比較每天多普勒解算軌道與基準軌道的差異，并統計RMS，結果顯示2種數據源解算軌道有較好的一致性(如圖12所示)，兩者的差異小于40 m(2組結果小于70 m)。

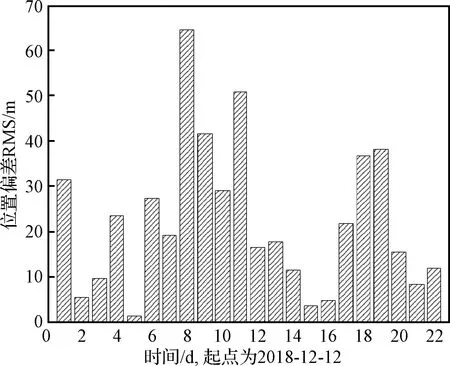
圖12 多普勒定軌與測距+VLBI定軌的比較Fig.12 Comparison of doppler-only and ranging+VLBI orbits

5 結 論

對嫦娥四號著陸器環月階段的多普勒測量數據進行處理。中國深空網佳木斯與南美測站的多普勒測量數據精度水平相當，定軌殘差RMS大約為0.3～0.8 mm/s，喀什站數據精度水平稍差，大約為0.6～1.2 mm/s。頻繁的姿控噴氣及對日定向偏置對著陸器產生細微的加速度，對軌道計算會產生20～50 m的影響。通過重疊弧段軌道比較，基于多普勒數據獨立解算軌道的三維精度為5～50 m。通過與測距及VLBI解算的軌道進行比較，兩種數據源解算軌道精度相當，整體差異為小于50 m。