主從式編隊航天器連通性保持與碰撞規避
薛向宏,岳曉奎,袁建平
(1. 西北工業大學航天學院,西安 710072;2. 航天飛行動力學技術重點實驗室,西安 710072)
0 引 言
相比于傳統的單個航天器,編隊航天器具有靈活性好、可靠性高、成本低等優勢[1-2],因此在合成孔徑雷達、重力場測量、天基干涉儀和分離模塊航天器等領域有著廣泛的應用[3-4]。文獻[5]對目前已有的航天器協同控制方法進行綜述,主要包括主從式方法、基于行為的方法、虛擬結構方法、循環追蹤方法、人工勢函數方法、代數圖方法和非接觸式方法等。
航天器編隊過程中的碰撞規避是完成其他一切任務的基礎。在執行跟蹤和編隊構型保持等任務時,必須防止航天器之間的碰撞規避。文獻[6-8]對編隊協同過程中的碰撞規避問題進行了研究,分別利用基于行為的方法[6-7]和勢函數法[8]實現了編隊過程中航天器之間的碰撞規避。文獻[6-7]采用的零空間法是一種典型的基于行為的編隊協同控制方法。該方法將低優先級任務的速度投影到高優先級任務的零空間中得到各個航天器的期望軌跡,然后再設計控制器對期望軌跡進行跟蹤。雖然零空間法能夠靈活地應對不同的任務要求,但是該方法得到的期望速度可能不連續,這會導致在某些時刻對控制器的輸入需求為無窮大。文獻[8]利用勢函數研究了驅動非完整時的編隊協同控制問題。勢函數法由于原理簡單,且易于和控制器相結合,在編隊協同控制中有著廣泛的研究。
文獻[9-14]針對主從式航天器編隊設計了分布式協同控制器。文獻[9]通過利用勢函數與非線性觀測器相結合,實現了高精度的分布式衛星協同控制。文獻[10]針對雙星編隊過程中主航天器軌道參數、軌道位置和軌道機動信息未知的情況,提出了一種自適應的控制方法。文獻[11-12]研究了主從式航天器編隊中的碰撞規避問題,但是文中假設所有航天器的狀態都是全局已知的。文獻[13]針對主從式衛星集群系統的空間構型長期保持問題提出一種控制算法。文獻[14]以線性雙積分系統的循環追蹤算法為基礎,設計了航天器編隊六自由度協同控制的循環追蹤算法。上述文獻都沒有考慮航天器之間的通信距離約束,都假設航天器之間的通信網絡在整個編隊過程中都是連通的。但是,由于航天器之間通信距離有限,編隊過程中航天器之間的相對位置的變化可能破壞航天器通信網絡的連通性。因此,需要在衛星協同控制中考慮通信網絡的連通性。文獻[15]利用勢函數給出了一種同時考慮航天器之間碰撞規避和通信網絡連通性保持控制方法,但是該研究中沒有考慮存在主航天器的情況。
目前少有文獻同時考慮主從式航天器通信網絡連通性保持和航天器之間的碰撞規避問題。本文針對主從式航天器系統,將勢函數、滑模控制和非線性干擾觀測器相結合,提出了一種分布式的航天器協同控制方法。具體來說,首先利用勢函數分別設計了排斥勢函數和吸引勢函數,分別用于實現航天器之間的碰撞規避以及通信網絡的連通性保持。其次,針對主航天器速度僅對部分從航天器已知的情況,設計了分布式的速度觀測器。此外,利用干擾觀測器對空間環境中存在的J2項攝動和大氣拖拽等干擾進行估計,從而實現高精度的編隊協同控制。最后,利用李雅普諾夫函數和仿真分析校驗了所提出方法的有效性。
1 相關基礎
1.1 相對動力學方程
(1)
式中:

1.2 圖 論




1.3 通信網絡初始化
首先對通信網絡進行初始化。航天器i的安全區域和通信區域在二維平面的投影如圖1所示,其中δij表示航天器i和j之間的安全距離,Δ為航天器之間的通信距離。由圖1可知,航天器i與航天器j之間發生了碰撞,航天器i與航天器l之間無通信,航天器i與航天器k之間存在通信連接且無碰撞發生,稱航天器i與航天器k之間存在一條邊。

圖1 安全和通信區域二維示意圖Fig.1 Two-dimensional illustration of collision and communication areas
根據上述模型,從航天器之間的鄰接矩陣元素可以定義為
(2)

(3)
式中:pi 0=pi-p0,p0表示主航天器的位置矢量。由上述定義可知從航天器之間的通信網絡是無向的,主航天器與從航天器之間的通信連接是有向的。
1.4 問題描述
本文的主要目的是實現在主航天器的狀態僅對部分航天器已知、空間干擾未知條件下的主從式航天器系統分布式協同控制。在編隊過程中防止航天器之間發生碰撞,且保證航天器通信網絡的連通性。上述描述可以敘述為如下形式。
問題 1:考慮由式(1)描述的航天器系統,假設初始時刻從主航天器到任意從航天器都存在著至少一條有向路,設計分布式協同控制器和干擾觀測器,使得如下結論成立:
(1)對于?t≥0,主航天器到任一從航天器都存在著有向路。
2 勢函數和控制器設計
2.1 人工勢函數設計
為了實現通信網絡的連通性保持和航天器之間的碰撞規避,設計如下人工勢函數
(4)

各部分勢函數具有如下性質:
(1)ψij是對稱函數,且滿足▽piψij=-▽pjψij。其中,▽piψij表示函數ψij在向量pi方向上的梯度。


2.2 主航天器速度恒定
本節研究主航天器速度恒定時的航天器編隊控制器設計。為了便于后續分析,定義如下輔助參數
(5)

(6)
設計如下分布式協同控制器、速度估計器和干擾觀測器
(7)
(8)
(9)
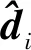
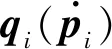
證. 對式(5)求導并將式(1)和式(7)代入可得閉環方程
(10)
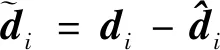
定義如下李雅普諾夫函數
V=V1+V2+V3
(11)
式中:
(12)
(13)
(14)
(15)
對式(13)求導可得:
(16)

(17)
(18)
將式(9)和式(18)代入式(14) 并求導可得
(19)
式(15)、式(17)和式(19)相加,并將式(8)代入可得
(20)

(21)

2.3 主航天器速度變化
第2.2節研究了主航天器速度恒定時,編隊衛星的協同控制,本節進一步考慮當主航天器速度動態變化時的航天器編隊控制器設計。首先對主航天器的加速度做出如下假設。
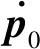
設計如下控制器和主航天器速度估計
(22)
(23)
式中:sgn(·)表示符號函數。
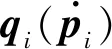
證. 將式(1)和式(22)代入式(2) 并求導可得閉環方程
(24)
考慮李雅普諾夫函數
V=V1+V2+V3
(25)
對式(25)求導并代入式(24)可得
(26)
將式(23)代入式(26)可得
(27)

(28)
假設圖的通信網絡只在時刻t=t1,t2,…發生變化,其他時間段固定不變。對時間t用歸納法:

(29)
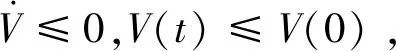
(30)

3 仿真校驗
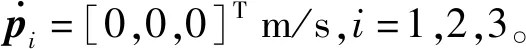
di=[5,5,5]T·sin(2πnct+iπ/10)
(31)
式中:nc為參考軌道平均角速度。
為了實現主從式航天器的協同控制,排斥勢函數、吸引勢函數和編隊勢函數的設計與文獻[17]類似
(32)
對上述勢函數分別求偏導可得
(33)
容易驗證上述勢函數是連續的,且滿足第2.1節中勢函數的性質。
3.1 主航天器速度恒定


表1 航天器的位置Table 1 The initial position of spacecraft

圖2 通信網絡Fig.2 The communication graph
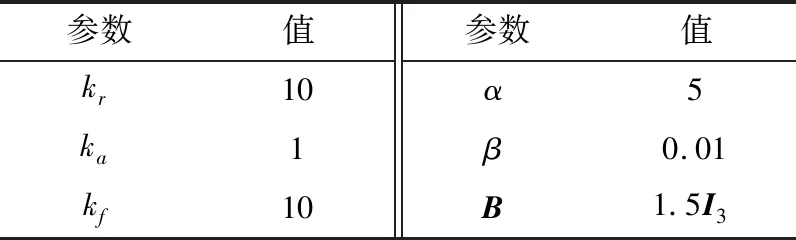
表2 控制器參數Table 2 Parameters of controller

表3 控制器參數[12]Table 3 Parameters of controller[12]
圖3~4分別給出了從航天器之間的距離、從航天器和主航天器之間的距離隨時間變化的曲線,其中實線表示航天器之間的通信距離。圖3(a)和圖4(a)為采用文獻[12]中控制器得到的仿真結果,圖3(b)和圖4(b)為采用本文提出控制器得到的仿真結果。由圖3(a)可知,在編隊過程中三個從航天器之間的距離在t∈(10,100) s時,其距離均大于航天器之間的通信范圍。因此,在實際情況下編隊通信網絡被破壞,航天器之間相互失去聯系。作為對比,圖3(b)中從航天器1和2以及航天器2和3之間的距離始終小于航天器的通信范圍。因此,航天器之間的通信網絡一直是連通的,航天器之間可以利用通信網絡實現最終的編隊。由圖4可知在兩種情況下,所有航天器都能夠實現期望構型。圖5和圖6分別為從航天器和主航天器速度誤差以及從航天器加速度隨時間變化的曲線。圖5表明本文提出的分布式協同控制算法能夠使得所有從航天器與主航天器之間的速度跟蹤誤差最終趨于零。由圖6可知從航天器的加速度最終也趨于零。

圖3 從航天器之間的相對距離Fig.3 The distance between the followers
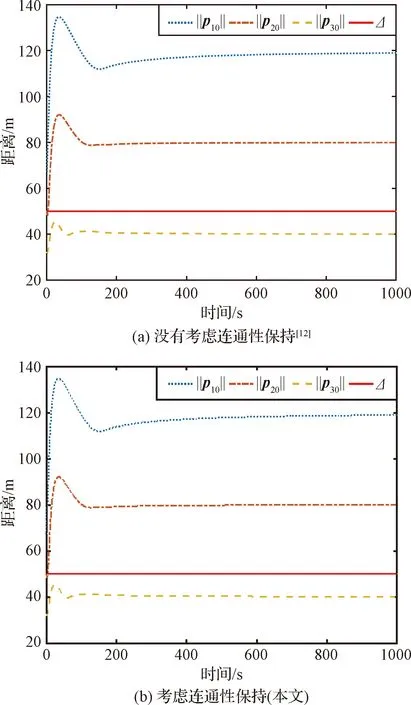
圖4 從航天與主航天器之間的距離Fig.4 The distance between the followers and the leader

圖5 速度跟蹤誤差Fig.5 The velocity tracking errors

圖6 從航天器的加速度Fig.6 The acceleration of the followers
為了說明本文中干擾觀測器對航天器編隊精度的影響,將仿真時間延長到12000 s。圖7為航天器1所受的干擾和干擾估計的差值隨時間變化的曲線圖。由圖7可知干擾觀測器精度為10-5m。圖8對比了在有無干擾觀測器的情況下,航天器1和航天器2之間的距離與期望距離差的精度。由圖8可知,在無干擾觀測器的情況下,編隊跟蹤誤差精度為10-2m,而采用了干擾觀測器之后,跟蹤誤差精度提升到了10-5m。

圖7 干擾估計差值Fig.7 The disturbance estimation errors

圖8 航天器1和航天器2之間的距離跟蹤誤差Fig.8 The distance tracking error between spacecraft 1 and 2
3.2 主航天器速度變化


表4 航天器的位置Table 4 The initial position of spacecraft

圖9 通信網絡Fig.9 The communication graph
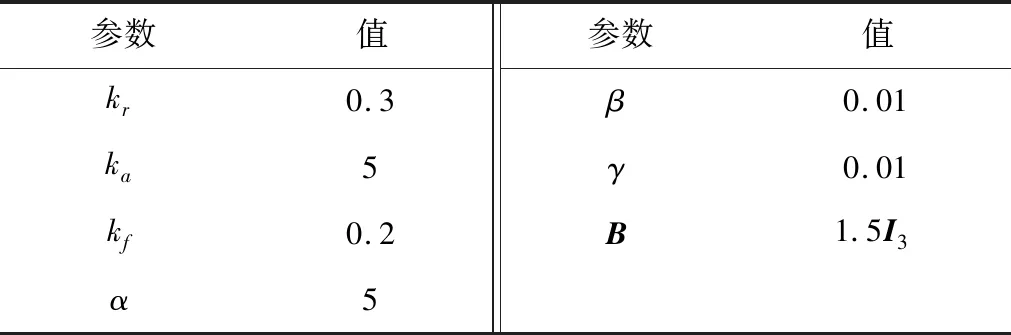
表5 控制器參數Table 5 Parameters of controller

表6 控制器參數[12]Table 6 Parameters of controller[12]
圖10~11分別給出了從航天器之間的距離、從航天器和主航天器之間的距離隨時間變化的曲線,其中實線表示航天器之間的通信距離。圖10(a)和圖11(a)為文獻[12]中的沒有考慮通信網絡連通性的仿真結果,圖10(b)和圖11(b)為本文的仿真結果。由圖10可知,在兩種情況下,從航天器1和2以及從航天器2和3之間的距離都小于航天器之間的通信距離,因此可以實現從航天器之間的期望構型。由圖11(a)可知,在文獻[12]中的控制算法作用下,當t=100 s時,所有從航天器與主航天器之間的距離都大于通信距離,這就導致了所有從航天器不能獲得主航天器的信息,從而不能實現對主航天器的速度和位置跟蹤。作為對比,由于采用了吸引勢函數,圖11(b)中從航天器2和主航天器之間的距離始終小于航天器的通信范圍。因此,航天器之間的通信網絡一直是連通的,從航天器可以實現對主航天器的速度和位置跟蹤。圖12和圖13分別為從航天器和主航天器速度誤差以及從航天器加速度隨時間變化的曲線。圖12表明盡管主航天器的速度是變化的,所有從航天器的速度都能夠與主航天器的速度達到一致,其速度跟蹤誤差為零。圖13表明從航天器的加速度最終收斂到零。

圖10 從航天器之間的相對距離Fig.10 The distance between the followers

圖11 從航天與主航天器之間的距離Fig.11 The distance between the followers and the leader

圖12 速度跟蹤誤差Fig.12 The velocity tracking errors

圖13 從航天器的加速度Fig.13 The acceleration of the followers
4 結 論
對于主從式編隊系統,航天器之間通信網絡的連通性是實現航天器分布式編隊協同的基礎。本文利用勢函數和干擾觀測器分別給出了主航天器速度恒定和變化時候的分布式協同控制器。該方法能夠在航天器之間通信距離有限的約束下,且航天器之間通信網絡在初始時刻連通時,能夠保證該動態網絡在編隊協同控制過程中始終連通。從而保證了航天器編隊任務的順利實施。

