溫度-孔隙水壓耦合作用下砂巖卸荷損傷本構模型研究

郭永成，劉鑫宇，王克輝，胡 鵬

(1.三峽庫區地質災害教育部重點實驗室，湖北 宜昌 443002；2.防災減災湖北省重點實驗室，湖北 宜昌 443002；3.三峽大學土木與建筑學院，湖北 宜昌 443002)

0 引 言

巖石的本構關系是巖石力學研究的關鍵問題。地下工程開挖深度較大，而內部巖石在地熱能的作用下會有高溫存在，高溫的長期作用會加劇巖石內部裂紋的發展。同時，開挖過程會伴隨著溫度的變化，不同溫度下底部巖石的地應力會發生改變，也會帶來巖石變形的改變，而工程建設是否安全的最直接的依據就是巖石的變形量。深層工程開挖過程中，除了溫度變化外，地下水位也對開挖影響較大。因此，結合實際開挖工程，開展溫度-孔隙水壓作用下的砂巖卸荷力學特性研究，基于此條件推導相應的本構方程，對深入理解砂巖卸荷力學問題具有重要的現實意義。王震等[1]開展了凍融作用下巖石力-熱-水耦合試驗，推導出力-熱-水三場耦合下的巖石本構模型；劉俊[2]開展高應力、高水壓下砂巖卸荷試驗，基于試驗結果提出改進的Duncan-Chang本構模型，建立符合卸荷條件下的線彈塑性分段模型，并將試驗結果與理論模型進行對比驗證；李濤[3]開展不同卸荷方式下的粉砂巖卸荷試驗，結合不同條件試驗的結果，區別探討不同強度準則的適用性，并將卸荷破壞過程分段，分別建立每一段的本構模型；王興霞等[4]開展升軸壓峰前卸圍壓、軸壓和圍壓等量減小2種應力路徑下的砂巖卸荷試驗，利用Hoek-Rrown準則推導出增量形式的卸荷彈脆塑型本構模型，并驗證了模型的正確性；李宏哲等[5]開展大理巖加卸荷變形特性試驗，利用M. C. Weng等人提出的各向異性非線性模型描述砂巖的變形特征，在變形模量弱化規律中引入了系數R，修正了Weng模型中的不足；張嘉威[6]開展巖石三軸壓縮試驗，采用修正的Harris函數和Hoek-Brown準則，建立巖石在三軸壓縮條件下的全過程損傷本構模型；Lau等[7]驗證了利用卸荷路徑獲取的力學參數和實際開挖工程的工況更為匹配；Wu等[8]開展巖石卸荷試驗，建立巖石卸荷的本構模型；Li等[9]開展不同溫度下的巖土體的損傷試驗，基于M-C屈服準則，推導出巖土材料的損傷本構模型。此外，文獻[10-16]對巖石在溫度場下的力學特性開展了較全面的試驗分析。

以上研究為正確認識多場耦合作用下的巖石損傷機理奠定了基礎，但對溫度-水壓耦合作用下的砂巖卸荷損傷本構關系研究比較少。為此，本文以湖北省白水河滑坡段砂巖為試驗對象，在室內試驗結果及其分析的基礎上，考慮溫度-孔隙水壓對砂巖損傷的影響，運用孔隙水壓作用過程中的能耗關系作為損傷變量，基于最小能耗原理，推導并驗證溫度-孔隙水壓耦合作用下砂巖卸荷損傷本構模型。

1 試驗設計

1.1 試驗儀器

試驗儀器為TOP INDUSTRIE公司和法國里爾科技大學合作共同研發的試驗機(見圖1)。該儀器的體積及壓力控制高壓液壓泵采用高級無電刷伺服機驅動液壓泵，通過高精度傳感器和伺服編碼器實現閉環回路控制。溫度控制主要采用加熱元件直接纏繞在壓力室表面給壓力室及加熱，控制精度可達到±0.1 ℃。同時，該儀器的一套多通道PC控制系統可獨立伺服控制軸向壓力、徑向壓力、孔隙水壓力和測試溫度，以保證試驗中溫度不受孔隙水壓等因素變化的影響。

圖1 TOP INDUSTRIE巖石三軸流變儀

1.2 試驗方案

本次試驗所需的巖樣全部取自三峽庫岸邊坡中的白水河滑坡段。基于試驗儀器及規范要求，砂巖巖樣尺寸符合國際標準(直徑50 mm、高度100 mm的圓柱體)。其誤差需滿足規范要求：高度及沿高度方向的直徑誤差應控制在0.3 mm以內；端面不平整度應控制在0.05 mm以內；端面垂直軸線的偏差應控制在0.25°以內等。制樣完成后，先將試樣烘干，再利用真空飽和儀進行飽和，最后對飽水砂巖試樣進行強度試驗。對1組試樣進行不同初始圍壓(5、10、20 MPa)下的單、三軸抗壓試驗，獲得峰值強度。利用儀器溫度控制系統加熱試樣至預定值(20、40、60℃)后，維持目標溫度6 h以上，確保受熱均勻；加載圍壓至目標值(5、10、20 MPa)后維持恒定；加載水壓至預定值(0.3、0.6、1.2 MPa)后，維持30 min；加載偏壓至抗壓強度的80%后維持恒定；以0.2 MPa/min的速率卸荷至巖樣破壞，停止試驗，取出試樣。為剔除離散性，每組試驗取3個試樣。

1.3 試驗結果

溫度-水壓耦合作用下砂巖力學參數關系見圖2。從圖2可知：

(1)砂巖的彈性模量與溫度呈反比例增長的關系，即溫度越高，彈性模量越小。這是由于溫度增加，砂巖內部的細小顆粒將發生膨脹產生新的裂紋，從而會使結構弱化導致的；砂巖在某一恒定溫度環境下，彈性模量隨水壓的增大而降低，且水壓越大，彈性模量降低的幅度也越大。溫度環境越高時，低水壓時彈性模量降低幅度不明顯，但會隨水壓增大而使降低幅度增大。

(2)砂巖軸向峰值應變表現為隨溫度的升高而降低，溫度越高時，峰值應變值越小，最后減小的差量及降幅趨于穩定，曲線逐漸趨于平緩狀態。

(3)砂巖的粘聚力c、內摩擦角φ均隨溫度和孔隙水壓的升高而降低，變化趨勢大體上相同。砂巖在溫度環境下，粘聚力隨著水壓的增大而下降，水壓力越大，粘聚力的劣化趨勢和幅度越明顯，相鄰2個水壓條件下的變化幅度也越大；低水壓作用時，各溫度環境間的粘聚力變化量一般比在高一級水壓作用時的變化量要小，說明孔隙水壓對粘聚力有影響。砂巖在相同的溫度環境下，內摩擦角φ與水壓表現為負相關關系，水壓力越大，內摩擦角的劣化趨勢與粘聚力的趨勢相似，其變化趨勢會有一些不同，尤其是溫度越高不同之處越明顯；低水壓作用時，各溫度環境間的內摩擦角變化一般比在高一級水壓作用時的變化量要小；相鄰2個溫度條件下的內摩擦角變化差值不同，低水壓時內摩擦角的下降趨勢在高一級溫度環境下會減緩，而在高水壓時則會加快，并且其變化有一定的規律。

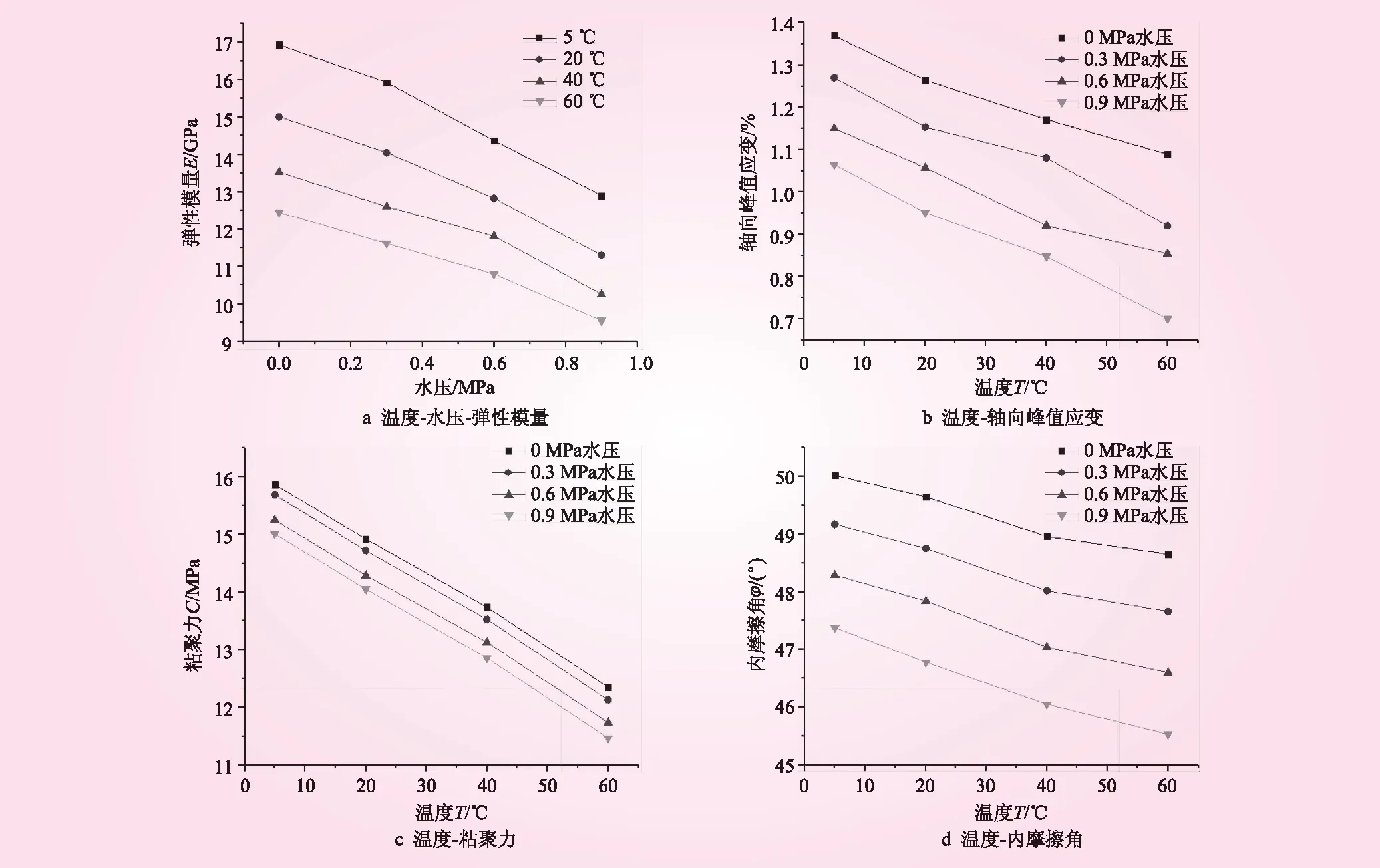
圖2 溫度-水壓耦合作用下砂巖力學參數關系

2 砂巖損傷本構方程

從試驗數據分析中可知，溫度對砂巖試樣的彈性模量影響比較明顯，故選定彈性模量來描述砂巖試樣在損傷狀態時的變量，將熱損傷D定義為

(1)

式中，ET為溫度T作用時室內試驗得出的彈性模量值；E0為初始溫度時砂巖的彈性模量。在不考慮巖石的初始損傷情況下，巖石各力學指標在不同溫度作用下呈弱化趨勢，20 ℃時的弱化趨勢最不明顯，故認為20℃時的砂巖試樣處于無損傷狀態(D=0)，即用巖石室溫時的彈性模量作為初始彈性模量E0。

試驗所使用的巖樣由于內部存在裂隙、雜質等，使試樣各微觀單元的強度存在差異性，排列具有隨機性。為了能更好地描述和分析微元體的強度特性，提出以下假設：①巖石內部的微觀單元體在宏觀上表現出各向同性；②巖石內的微元體的損傷具有各向同性；③巖石內各微元體破壞前符合廣義胡克定律；④巖石發生彈性變形前的損傷不發展是由溫度與孔隙水壓共同作用的；⑤巖石在試驗前沒有產生初始損傷，隨溫度升高和孔隙水壓增加，損傷值逐漸增加；⑥服從Weibull分布規律。公式為

(2)

式中，k為砂巖各微元體強度Weibull分布的分布變量；m、F為Weibull的分布參數。

砂巖內部損傷的過程是砂巖內部裂隙在外荷載的影響下發育、擴展的過程，這一損傷過程與砂巖內部產生損傷的微元體個數有著最直接的關系。即

(3)

式中，Nf為損傷微元體的個數；N為砂巖總微元體個數。式(3)中，k=0時，D=0，結合式(2)、(3)得到損傷變量D的表達式為

(4)

3 溫度-孔隙水壓耦合作用下砂巖卸荷本構研究

3.1 損傷理論基礎

巖石損傷變形實質是由于巖石內部產生能量轉化過程，是造成巖石產生損傷的本質屬性[17]。本文擬運用孔隙水壓作用過程中的能耗關系作為損傷變量，建立一個相對全面、宏觀的損傷變量。基于最小能耗原理，砂巖損傷變量Dw定義為砂巖卸荷破壞過程中所釋放的耗散能U耗與所吸收的總能量U總之間的比值，并將卸荷過程中的彈性應變能U彈與總能量U總的比值定義為彈性能占比系數ζ，即

(5)

由于水壓作用下的砂巖損傷過程并不是簡單地將水壓損傷與應力損傷損傷進行疊加，需根據等效原理推導出水壓作用下砂巖卸荷過程中的總損傷變量Ds[18]，即

Ds=D+Dw-DDw

(6)

將式(4)、(5)代入式(6)，得出砂巖在水壓作用下卸荷過程中綜合損傷變量計算公式為

(7)

根據式(5)計算出不同卸荷條件下，砂巖損傷的損傷變量Dw與彈性能占比系數ζ，并進行統計，結果見表1。

砂巖試樣內部微元體采用摩爾-庫倫準則作為其破壞依據，即

(8)

(9)

考慮本文所進行的試驗為假三軸試驗，即σ2=σ3，且試樣在每個溫度下的水壓試驗環境是恒定的，不存在由于溫度差產生熱能的損失，由胡克定律得

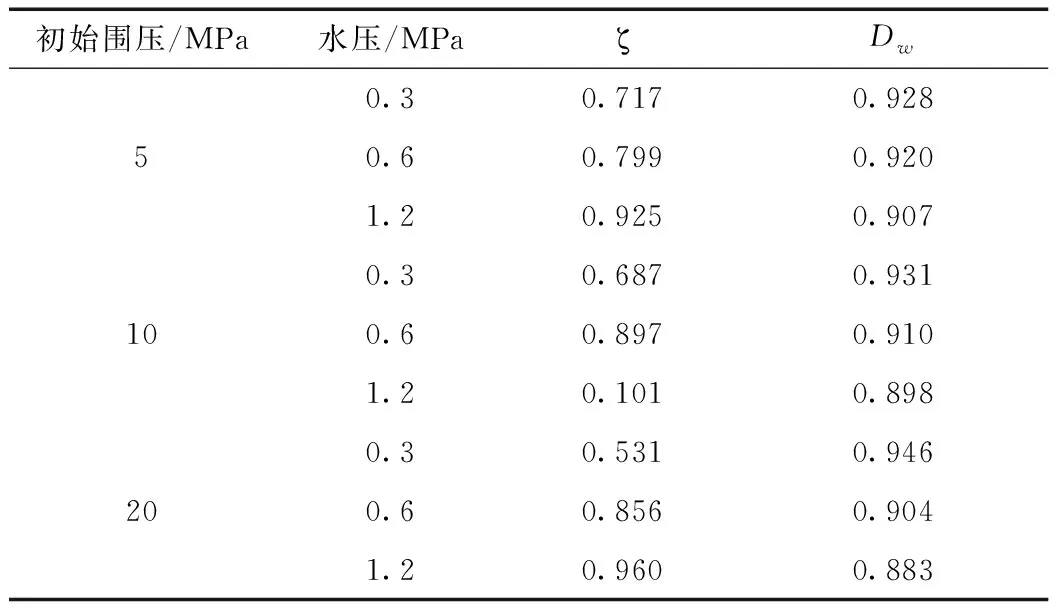
表1 不同卸荷條件下ζ和Dw統計結果

(10)

式中，ν為泊松比。由于本文試驗為假三軸試驗，即σ2=σ3，將式(10)代帶入式(9)可得

(11)

砂巖的損傷受孔隙水壓作用的影響，從該試驗結果中可知孔隙水壓與彈性模量、內摩擦角之間的關系，即

(12)

式中，Ep和φp分別為在有孔隙水壓下試樣的彈性模量和內摩擦角；A、B、C、a、b、c均為參數。

將式(12)代入式(11)得到砂巖試樣在考慮孔隙水壓時損傷演化方程為

(13)

式中，E、φ分別為在沒有孔隙水壓(p=0)時試樣的彈性模量、內摩擦角。

3.2 小能耗原理的溫度-水壓作用下砂巖卸荷損傷本構模型構建

不同溫度下砂巖試樣的均勻性、彈性模量、峰值強度也不盡相同，即

m(T)=(1-DT)m0
F(T)=(1-DT)F0

(14)

式中，m0、F0分別是試驗初始時溫度(5 ℃)下的Weibull的分布參數。把式(14)代入式(13)可得

(15)

根據Lemaitre[19]提出的應變等效假設式及連續損傷理論、巖石內部微元體在破壞前服從廣義胡克定律，有

(16)

結合本三軸試驗的應力條件σ2=σ3及式(16)進行整理變形得

σ1=Eε1(1-D)+2vσ3

(17)

將式(1)、(17)代入式(15)，整理得到砂巖試樣在考慮溫度效應及孔隙水壓時損傷演化方程為

(18)

式中，ET.P為T溫度和P水壓下的彈性模量。

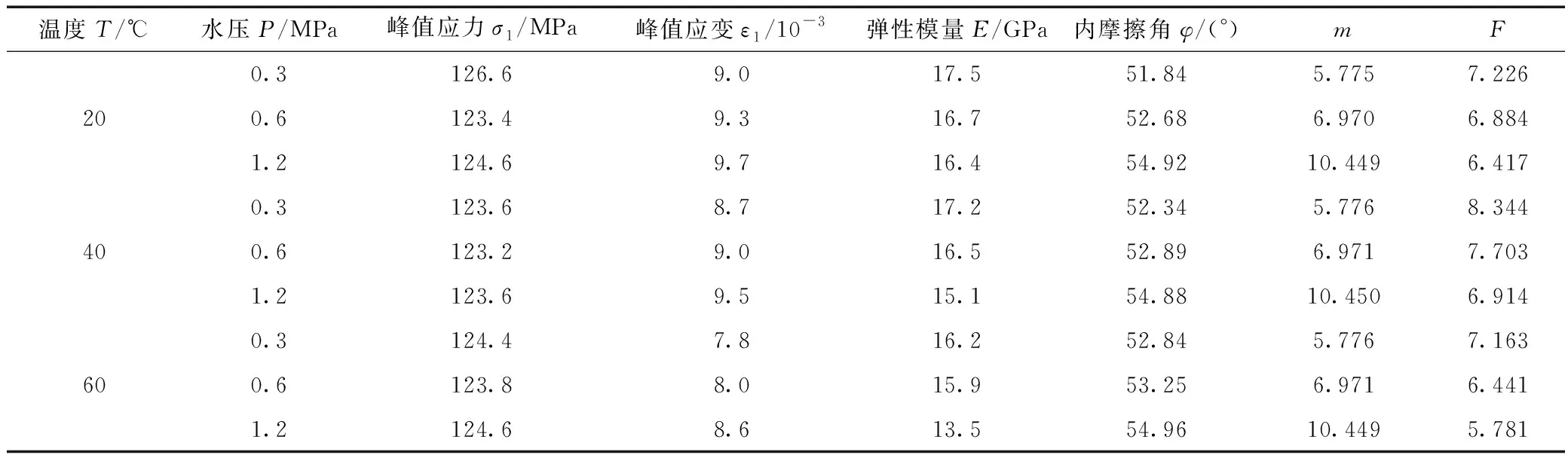
表2 砂巖試樣試驗曲線擬合計算結果

3.3 模型參數推導

前文所推導本構模型中，存在Weibull分布中F、m這2個未知的分布參數，這2個未知參數的確定需要引入卸荷破壞點p(σp，εp)，即

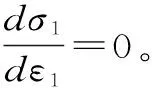
考慮情況①，代入式(18)可得

σ1p=ET.Pζε1pexp[-(Eε1p(σ1p-σ3)-(σ1p+σ3)sinφ/2F(σ1p-2vσ3))m0(ET/E0)]+2vσ3

(19)

將式(19)改寫為

(20)

考慮情況②，并對(18)求微分后可得

(21)

由于ET.Pζexp[-(ET.Pε1(σ1-σ3)-(σ1+σ3)sinφ/2F(σ1-2vσ3))m]≠0，故整理后可得

(22)

聯立式(20)、(22)，求解得

(23)

(24)

將試驗得到的數據，代入式(23)、(24)中，通過曲線擬合的方法依次求得損傷本構方程中的2個重要的分布參數m、F的值。本文選取圍壓為10 MPa(σ3=10 MPa)時對應的三軸試驗數據(見表2)。根據損傷本構方程求解得到砂巖試樣在不同溫度-孔隙水壓作用下的分布參數m和F。

從表2可知，損傷本構模型參數m、F并不是固定值，會隨著溫度與水壓的變化而改變。大體呈現出Weibull分布參數F會隨著溫度升高而下降，隨著水壓增大，m增大F減小，說明砂巖試樣在此耦合作用下的宏觀強度逐漸降低。分析表2并建立參數與溫度-水壓的關系，進而得出任意溫度-水壓下的損傷本構模型。由試驗數據對參數m、F擬合可得

m=73.41+1.243E-31.033ln(0.756 5+E0.975 8)

(25)

F=-0.23+0.023E+3.609e(0.065E+0.12)

(26)

結合式(17)、(20)、(22)，將上述擬合所得式(25)、(26)代入損傷本構方程中，得出溫度、孔隙水壓耦合作用下的砂巖的損傷本構方程的經驗公式

(27)

3.3 本構模型驗證

限于篇幅，本文選取10 MPa圍壓、0.6 MPa孔隙水壓條件下的試驗數據驗證。將求出的參數m和F以及試驗數據代入本構模型式(18)，得到σ1-ε1的函數關系，然后分別繪制出在相應試驗條件下的應力-應變關系曲線，并與實際的試驗曲線對比，引用文獻[20]中基于常規損傷變量的卸荷巖石的統計損傷本構模型，與本文所建立的基于最小能耗原理的卸荷巖石的損傷本構進行對比驗證。應力-應變曲線試驗值與模型值對比見圖3。從圖3可知，本文所建模型的理論曲線與試驗曲線吻合較好，平均相關性系數為0.937 4，誤差較小，而文獻[20]模型的理

圖3 應力-應變曲線試驗值與模型值對比

論曲線平均相關性系數僅有0.795 3，實際工程應用可能會出現較大誤差甚至偏于危險。說明考慮溫度-孔隙水壓耦合作用下，砂巖卸荷過程中能量的損耗的影響是合理可行的，且可較好地反應溫度-孔隙水耦合作用對砂巖的損傷影響。砂巖的劣化損傷效應雖然在開始及破壞階段有些出入，即該模型的理論應力-應變曲線均隨溫度及水壓的增大，在破壞時的σ1和ε1應變都有一些延遲，這主要是因為在模型推導時引入的一些假設與實際的試驗過程存在誤差。

4 結 語

本文以湖北省白水河滑坡段砂巖為試驗對象，基于室內試驗數據，根據Weibull統計分布理論及廣義胡克定律，運用孔隙水壓作用過程中的能耗關系作為損傷變量，考慮溫度-孔隙水壓耦合作用下對砂巖損傷的影響，選取彈性能占比系數，并基于最小能耗原理，建立了溫度-孔隙水壓耦合作用下砂巖卸荷損傷本構模型，得出以下結論：

(1)在溫度-孔隙水壓耦合作用過程中，不同溫度及孔隙水壓會對砂巖試樣的內部不斷造成損傷，使其內部的結構弱化，從砂巖的彈性模量、峰值應變、粘聚力、內摩擦角等參數變化的規律可知，該作用不利于巖石的發育，而不同初始圍壓則會使應力-應變曲線的斜率變大，即彈性模量在逐漸增大。

(2)對比分析表明，所建立的損傷本構模型模擬曲線與試驗曲線整體上保持一致、相似程度較高，試樣破壞時的各軸向應力和應變均隨各試驗條件的改變而發生相應的變化，也表明了此本構模型有其實用意義。Weibull分布參數F會隨著溫度升高而下降，隨著水壓增大，m增大，F減小，說明砂巖試樣在此耦合作用下的宏觀強度逐漸降低。