基于有序聚類的發動機溫度劃分研究

石 鋒，補 涵，賀玉龍，陳兵碩，崔世超，王慶陽，譙 鑫，賀曉娜

（1.中國汽車工程研究院，重慶 401122；2.北京工業大學，北京 100124；3.長安大學，西安 710064）

溫度是熱量不斷積累的結果。汽車正常行駛時，發動機在不停地工作，因為發動機冷卻系的作用，使發動機產生的多余熱量能夠快速散發出去，從而使發動機在良好的狀態下工作。

發動機在冷卻水溫度為80～90℃時工作最佳，冷卻水溫度過低或者過高都會使發動機的排放、燃油消耗、使用壽命等受到很大的影響[1]。冷卻水溫度過低會使缸壁處于較低的溫度狀態，使缸內的燃油和空氣難以充分混合，導致可燃混合氣質量下降，汽車燃油經濟性下降[2]。潤滑油在低溫時黏度變大，使發動機內零件相對運動時的阻力增大，降低了發動機的輸出功率[3-4]。同時，在低溫情況下潤滑油因黏度大而難以形成潤滑良好的油膜，使發動機內各部件運動時的摩擦損失加大，摩擦產生的磨屑會加劇氣缸的腐蝕磨損[5]。冷卻水溫度過高，會導致發動機內部的金屬材料受熱膨脹，使其正常的工作間隙不能得到滿足，進而導致發動機工作粗暴，易出現活塞咬死、拉缸等故障[6]。同時，冷卻水溫度過高會使發動機內潤滑油因密度減小而變稀，加快潤滑油氧化變質的速度，使潤滑油膜質量變差進而加重氣缸磨損[7]。試驗表明，冷卻水溫度為50℃時，發動機磨損量是溫度為90℃的3倍；當溫度下降到40℃時，磨損量是90℃的5倍[1]。因此，保證發動機水溫處于正常范圍之內，對于降低發動機油耗，提升發動機性能，延長發動機壽命有著重要的意義。

1 問題描述

汽車在行駛過程中，發動機出水口溫度總是在不斷地改變。車輛在正常行駛工況下一般會經歷以下幾個階段：在剛啟動時會有一段熱車時間，此階段發動機溫度上升較快，當水溫表溫度上升至80℃左右時，車輛開始行駛；隨著發動機工作負荷的增大，出水口溫度會有所上升；當車輛行駛時間較長時，發動機出水口溫度會上升至某一較高溫度，此時，發動機輔助冷卻裝置工作，從而使發動機工作溫度降低，但溫度仍然處于一個較高的狀態。發動機冷卻水溫度與正常工作的溫度范圍偏離較大，因此，對車輛發動機出水溫度進行分析，可以判斷其是否處于正常狀態。通過采用Fisher有序聚類分析的方法對發動機出水溫度進行聚類分段[8]，對分段后的每一段發動機出水溫度進行分析，得出其是否處于正常工作狀態，輔以相應的發動機溫度調節措施，進而就能夠達到提升發動機性能、延長發動機使用壽命的目的。

2 劃分依據及意義

2.1 劃分依據

汽車在道路上行駛時，其發動機出水溫度是一組連續變化的有序數據，其排列順序不可打亂。因此，在數據分析時應當用到有序樣品聚類法。通過對汽車發動機工作過程中出水溫度的統計分析，采用Fisher最優分割法的聚類分析算法，對發動機出水溫度數據進行正規化處理，根據Fisher最優分割法的極差計算公式得出極差（或變差）矩陣，再由該矩陣計算全部分兩類的分割方法相應的總變差，找出其中最小值確定最優二分割點，得到最優二分割。在最優二分割的基礎上用相同的方法再進行最優三分割，依次產生最優k分割。最后計算每種分割方法的組內離差平方和，離差平方和最小的分割即為最優分割[9]。

2.2 劃分意義

采用Fisher最優分割法得到的最優分割數可使同類出水溫度之間的差別最小，不同類別出水溫度之間的差別最大。這樣即可結合發動機實際工作情況，將不同類別的出水溫度和相應的發動機工作狀況緊密聯系起來。通過對發動機出水溫度的連續測量便可了解到發動機所處的工作狀態，配合相應的發動機溫度控制措施，就可在一定程度上使發動機工作在最佳溫度范圍內，從而使汽車具有良好的燃油經濟性和排放特性，并延長發動機的使用壽命。

3 模型構建

3.1 Fisher最優分割法

有序樣品聚類法作為常用的一種聚類分析方法，與其它聚類方法的不同主要是在通常的聚類分析中，樣品之間彼此是平等的，聚類時是將樣品混在一起按照距離或相似系數的標準來進行分類，但有時在聚類時要求不能打亂原來樣品的排列順序，這個時候就要用到有序樣品聚類法[10-11]。

有序樣品的分類實質上是在樣本上找一些分割點，利用找到的這一系列分割點將一段按一定順序排列的樣品進行分割，分割得到的每一段都單獨看作一個類。可以看出，當分割點取在不同的位置時，就會得到完全不同的分割結果。要保證分割方法是最優的，首先要保證分割后的各段中內部樣品之間的差異最小，同時也要保證不同段樣品之間的差異最大，因此有序聚類法又叫做最優分割法[9]。

Fisher最優分割法的原理是通過計算樣本數據的離差平方和，以此反映同類樣本間不同數據的差別程度，并用規定的計算步驟確定最佳的分類數。確定分類數之后可以采用檢驗法來檢驗該最佳分類數的合理性[12]。這個最佳分類數就可以使不同類樣本之間的差別最大，而同類別樣本之間的差別最小。

以下兩個遞推公式是有序聚類過程的核心：

從上述公式可以看出，若想找到將n個有序樣品劃分成k類的最優分割方法，應當建立在把j-1（j=2,3,…,n）個樣品分成k-1類的最優分割方法的基礎上[13]。

3.2 基于Fisher最優分割法的聚類分析算法

3.2.1 數據正規化

設原始信息矩陣為：

將矩陣Y中的元素Yij變換為：

3.2.2 計算極差（變差）矩陣

由上述極差（變差）公式可得到矩陣：

3.2.3 進行最優二分割

由M矩陣計算所有分為兩類的不同分割方法對應的總變差，即把每一個m(m=N,N-1,…,2 )相對應的總變差Hij(j= 1 ,2, … ,m-1)計算出來并找出其中的最小值，以此得出各個子段的最優二分割點;α1(m))，即進一步就能確定將N個樣品進行最優二分割的分割方法[12]。最后，分別對每一種分割方法的組內離差平方和進行計算，并從計算結果中找出組內離差平方和最小的那組分割，即可得到所要求的最優二段分割[14]。在實際應用的過程中，往往很難得知這n個有序樣品在事實上究竟可以分為幾個子段。因此，必須先對樣本點進行二分割分析。

3.2.4 進行最優三分割

對于m=N,N-1,…,4,3，由3,4, … ,m-1)及M矩陣分別計算：

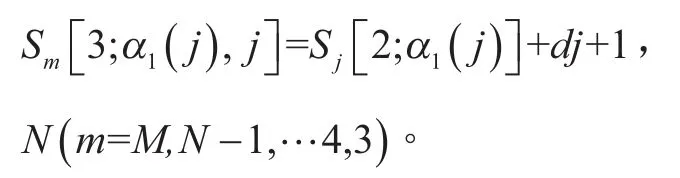
然后求出最小值，即：

從而得到N個樣品最優三分割：

3.2.5 進行最優k分割

重復上述步驟，在最優三分割的基礎上可以進行最優四分割，接著繼續進行最優五分割，依此類推，如果已經做出最優k-1分割，則可以產生最優k分割[15-16]。

4 實例分析與求解

根據有序聚類原理，以發動機出水溫度為聚類指標進行汽車發動機工況分析。采得試驗數據有效時長41 min。發動機出水溫度變化較慢，因此，每分鐘取一個樣本點進行分析。各樣本點數據見表1。

按照有序聚類方法的步驟，首先進行樣品正規化，結果見表2。

接著計算極差矩陣M，結果見表3。

由極差矩陣依次計算全部分成2、3、4類的各種分割方法對應的總變差，使組內離差平方和最小的分割即為最優分割，最終得到的最優k分割的k=3，具體結果見表4。

表1 各樣本點數據 ℃

表2 樣品點正規化

表3 極差矩陣

表4 最優分割結果

車輛發動機出水溫度隨時間變化曲線如圖1所示。

圖1 發動機出水溫度-時間曲線

由分割結果可知，本次所選道路被分割為4段，結合發動機出水溫度隨時間變化的曲線可以看出，車輛處于熱車狀態時，發動機剛啟動，出水溫度略有波動，大概在82～87℃范圍內波動；在第4 min末結束熱車，車輛開始正常行駛，發動機工作負荷逐漸增加，發動機出水溫度也逐漸上升。因為車輛在行駛過程中會經過各種不同的路段，擋位、車速都在不斷變化，所以發動機出水溫度也會略有波動，大致穩定在90℃左右，發動機工作狀態良好[8,17]；在第30 min末由于發動機出水溫度較高，發動機輔助冷卻裝置開始工作，所以發動機出水溫度略有下降的趨勢，但總體上仍是處于上升趨勢。隨著車輛繼續行駛，發動機出水溫度已經處于110℃左右，此時冷卻水溫度與正常工作范圍偏離較大，會在一定程度上導致發動機工作粗暴，汽車的油耗和排放也會明顯增加[18]。

5 結論

本文通過采用Fisher有序聚類方法對在道路上行駛的車輛發動機出水溫度進行聚類分析，得出車輛發動機在不同路段時的工作狀態。綜合來看，用有序聚類的方法可以得出汽車發動機在運行過程中出水溫度的變化規律，從而在一定程度上使發動機盡可能在最佳溫度范圍內工作，達到降低油耗，減少排放污染，提高發動機壽命的目的。