混凝土重力壩結構斷面優化設計研究

韓繼陽 ，韓 康 ，杜傳陽

（1.莒縣水利局，山東 莒縣 276500；2.德州市李家岸灌區管理局，山東 德州 253000；3.濟南市市政工程設計研究院（集團）有限責任公司，山東 濟南250000）

0 引言

重力壩斷面基本呈三角形，筑壩材料大多數為混凝土，這種壩稱為傳統的重力壩。據統計，在各國修建的大壩中,因傳統重力壩具有安全性高、耐久性和抗滲性好，設計、施工技術簡單，對不同的地形和地質條件適應性強等優點，在各種壩型中往往占有較大的比重。但同時也具有壩體應力較低，壩體體積大，耗用材料多等缺點。因此，從安全性、經濟性和美觀性出發，對傳統重力壩斷面進行優化設計尤為重要。本文采用一種新的斷面形式為曲線形式的重力壩[1]。本文以新建某樞紐工程重力壩為例，借助ANSYS軟件建立數學模型，求解優化設計變量，對優化結果進行分析；對曲線形式重力壩進行應力和抗滑穩定分析，并與傳統三角形斷面重力壩優化結果進行對比[2]。

1 數學模型的建立

1.1 設計變量

根據傳統重力壩與優化后重力壩橫斷面形式的不同，得到重力壩不同設計變量，傳統的重力壩根據其斷面形式需要取5個設計變量，即x1～x5，分別表示重力壩斷面的不同位置，優化后的重力壩斷面為曲面形式，設計中我們將重力壩斷面曲線擬定為y=ax2+bx+c的二次拋物線形式，選取上下游曲線方程系數a1，b1，a2作為本文模型設計變量[3]。兩種重力壩壩體斷面形式見圖1。

圖1 兩種重力壩體斷面形式

1.2 設計函數

（1）目標函數

本次設計主要是在滿足自重和抗滑穩定的情況下確定目標函數為求重力壩設計最小斷面A(x)，即求minA(x)，從而達到經濟、節省投資的效果。

（2）約束條件

本文建立目標函數，必須滿足以下約束條件:

幾何約束:a1＞0，a2＞0，a2≧0；

式中:Ks為抗滑穩定安全系數；f為抗滑穩定摩擦系數，取值區間0.5～0.8；ΣW為壩體所有荷載在豎向的分力總和，kN；ΣP為壩體上全所有荷載沿滑動面的分力總和，kN；U為壩體所受揚壓力，kN。

應力約束:

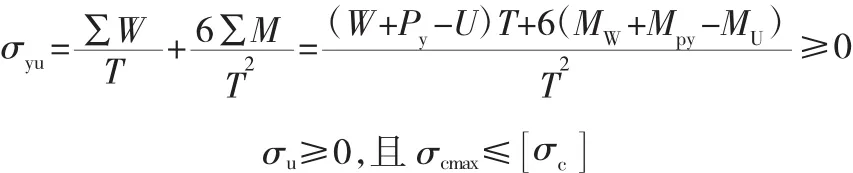
式中:σyu為壩踵處的豎向應力，MPa；ΣM為荷載對該截面形心的力矩總和，kN·m；MW、MU、Mpy分別為重力、揚壓力以及豎向分力對于計算截面形心處的力矩，kN·m；T為計算截面沿上下游方向的寬度，m；σu為壩體的上游邊緣處豎向應力，MPa。

1.3 曲線重力壩參數化建模

本文是通過大型有限元計算軟件ANSYS軟件進行重力壩斷面優化設計[4]，采用二維平面進行建模求解，得到有限元計算模型。

（1）參數設置

壩面曲線方程系數取值為:a1=1.1，b1=0.8和a2=0.5，γ為水的容重，揚壓力折減系數α取值0.2；抗滑穩定摩擦系數f取值為壩踵距壩頂距離為壩底寬度[5]。

（2）單元類型和材料屬性

本文中，對混凝土而言，彈性模量E=2.85×104MPa，密度ρ=2400 kg/m3，泊松比 ν=0.167；對基巖而言，彈性模量E=2.00×104MPa，密度 ρ=2600 kg/m3，泊松比 ν=0.300。壩體混凝土，本文采用PLANE82結構實體單元，模型的基巖部分，本文采用PLANE183結構實體單元，基巖范圍取上游1.5H，下游2H，壩基深為2H，曲線重力壩有限元網格劃分見圖2、圖3。

圖2 有限元模型網格劃分圖

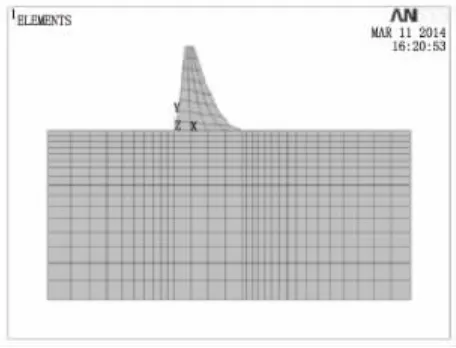
圖3 曲線重力壩優化模型

（3）約束與加載

在建立有限元模型時，沿壩體軸線的方向取x軸方向，沿重力壩壩體上、下游面上取y方向，建立坐標系，在重力壩壩基底面位置按照固定約束處理，在重力壩壩體上、下游面上（y方向）按照簡支約束設置，沿壩體壩軸線的方向(x方向)按簡支約束進行處理，為簡化計算模型，重力壩其他邊界以自由邊界進行考慮。

重力壩荷載主要由自重、靜水壓力、揚壓力和地震荷載進行組合加載[6]。在ANSYS中，常規重力壩和優化重力壩在材料參數、計算范圍、邊界約束條件、單元類型等是相同的。曲線重力壩優化模型圖見圖3。

2 優化結果分析

本文在ANSYS軟件有限元分析時，將零階分析得到的設計結果做為初值，再通過一階方法進行更加精確的計算分析[7]。重力壩優化后的設計變量值見表1。

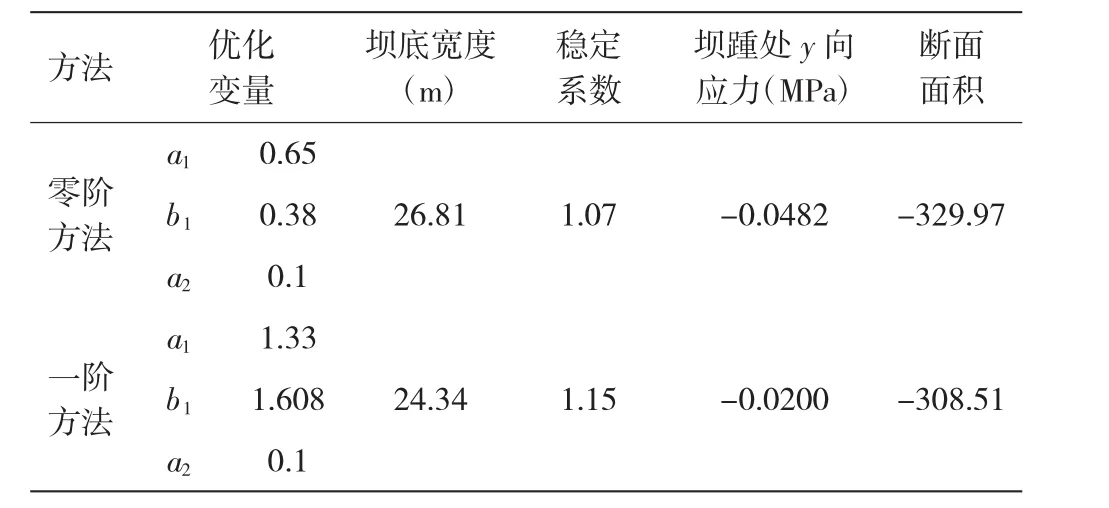
表1 重力壩優化后的設計變量值

2.1 靜荷載作用下壩體優化結果分析

靜荷載作用下曲線壩體y方向的應力和位移云圖見圖4。

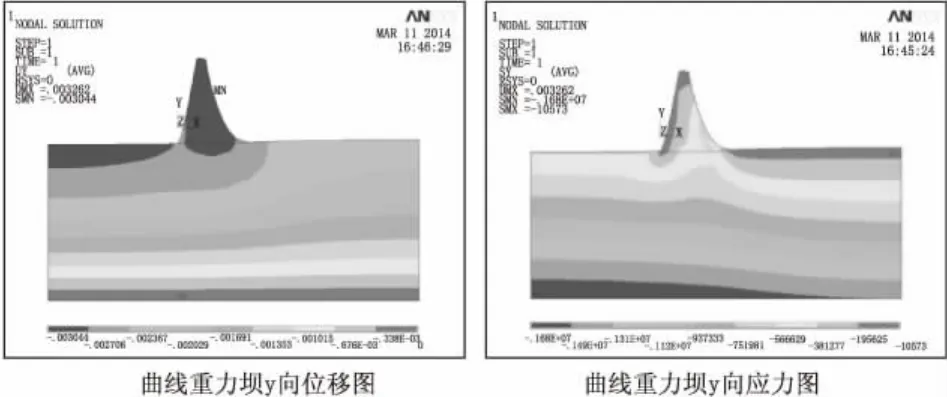
圖4 靜力荷載作用下曲線重力壩位移和應力云圖

由圖4可以看出，優化后的重力壩在靜荷載作用下，y方向的最大位移發生在壩體上，位移值很小，約3.2 mm，靜荷載作用下壩體壩踵位置不會產生拉應力，同時因壩體下游無荷載，壩體的垂直正應力發生在壩體下游基巖上，應力滿足設計要求。

2.2 壩體動力分析

動力分析是通過ANSYS對曲線重力壩進行模態分析[8～10]，振型圖見圖5。壩體在完成模態合并后便可得出壩體相應的位移和應力情況。在地震作用下曲線壩體y方向的部分應力和位移云圖見圖6、圖7。

圖5 模態分析下各階振型圖（部分）

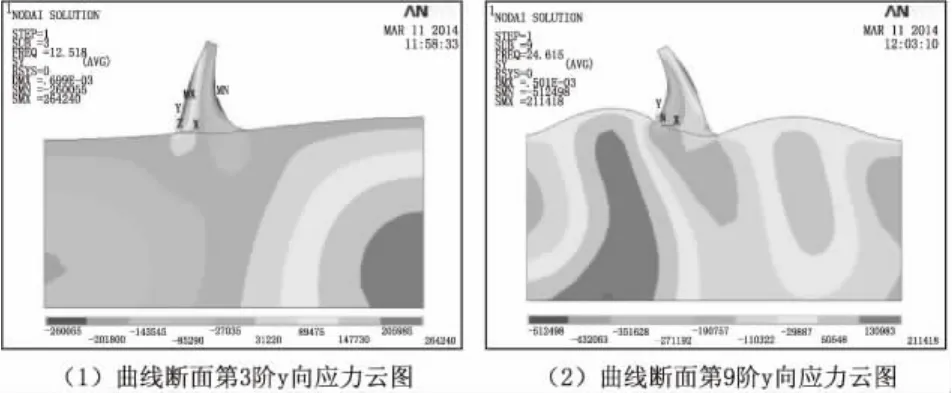
圖6 曲線重力壩抗震分析應力云圖

圖7 曲線重力壩抗震分析位移云圖

由圖6和圖7可知，重力壩在地震荷載作用下壩體的位移和應力都較受靜荷載作用時大，位移最大值為4.6 cm，但應力和位移最大值均滿足設計要求，最大應力和位移主要發生在基巖上。

2.3 基本斷面優化結果

為了更好的體現優化重力設計斷面的優越性，對原三角形重力壩斷面同樣進行了優化設計。優化后的傳統剖面圖見圖8，靜力荷載作用下第一主應力云圖見圖9，傳統三角形重力壩斷面優化結果見表2。

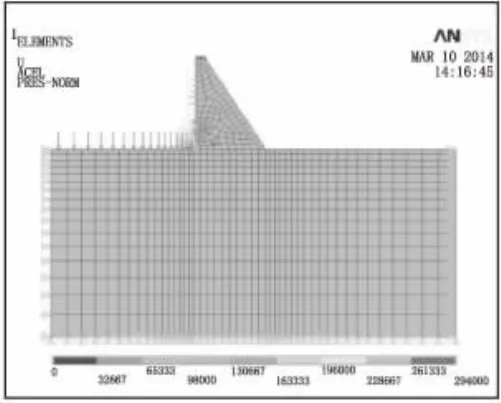
圖8 優化后的傳統剖面圖

圖9 靜力荷載作用下的第一主應力云圖

表2 傳統三角型重力壩斷面優化結果數據

傳統壩面在地震作用下，重力壩的最大位移出現在壩頂位置，其抗震分析的應力、位移云圖見圖10。由圖10可知，壩體的最大應力都發生在基巖上，壩體壩踵處的應力滿足要求。

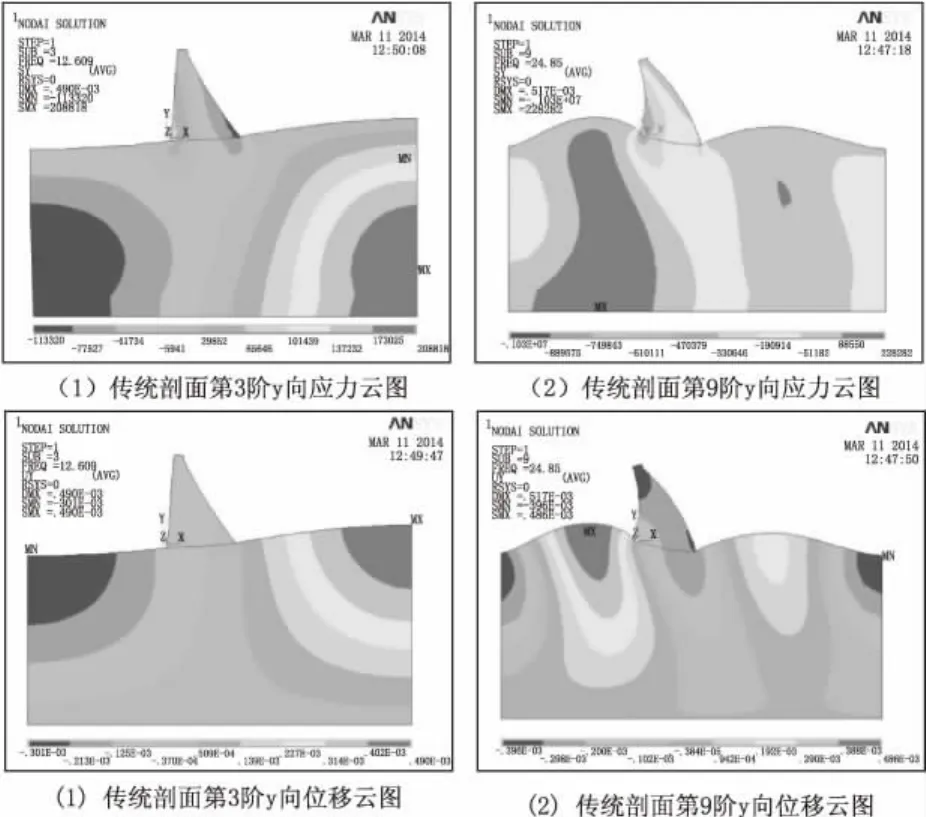
圖10 常規重力壩抗震分析應力、位移云圖

2.4 斷面優化結果對比

運用ANSYS軟件，對兩種斷面進行模擬分析[11]，現將相同壩高、相同材料、相同工況下的兩種不同斷面的結果進行對比，分析結果見表3。

表3 兩種壩型優化結果對比表

通過表3兩種對比結果可以看出，優化的曲線重力壩明顯優于同樣優化的三角形重力壩斷面，在ANSYS軟件經過0階和1階優化后，前者較后者在面積上減少16.6%，在經濟方面很有優勢。

3 結論

本文借助新建小（1）型水庫重力壩斷面設計，采用ANSYS軟件，兩種壩型在相同壩高、相同材料、相同荷載情況下，分別進行常規重力壩及曲線重力壩斷面優化并進行應力變形分析，得到兩種壩型在靜荷載和地震荷載作用下壩體應力變形均滿足規范要求，但曲線重力壩比基本三角形斷面更加節約材料，在經濟上占優勢；同時與三角形重力壩斷面相比，曲線斷面的壩底寬度加大而更加有利于壩體穩定。