基于數據驅動緊框架理論的三維地震數據去噪與重建

陳 杰 牛 聰 李 勇*③ 黃 饒 陳力鑫 馬澤川

（①成都理工大學地球物理學院，四川成都610059；②中海油研究總院有限責任公司，北京100027；③油氣藏地質及開發工程國家重點實驗室（成都理工大學），四川成都610059）

0 引言

三維地震勘探是油氣勘探的主要技術，包括地震資料采集、處理及解釋流程。由于受經濟成本、地質條件等因素限制，地震采集數據一般為欠采樣數據且含有噪聲［1-2］，將對數據處理和地質解釋產生嚴重影響。因此，三維地震數據去噪與重建是一個有重要意義的課題。

地震數據去噪方法很多，主要分為濾波法和數學變換法兩類。地震數據重建方法主要分為五類：預測濾波法、波動方程法、相干傾角插值法、矩陣降秩法和數學變換法。其中數學變換法是基于壓縮感知理論的一類稀疏變換算法，是目前較為主流的地震數據重建和去噪算法，如傅里葉變換［3-4］、Radon變換［5-6］、小波變換［7-8］、曲波變換［9-10］等稀疏變換算法。

上述傳統的基于變換域的去噪和數據重建算法都是對原始數據進行某種變換，然后在變換域對系數進行閾值處理，從而恢復高精度數據。傳統算法中稀疏變換的基函數一般是固定不變的，不同的稀疏變換局限于處理特定結構的數據，使這些算法無法適應結構復雜的地震數據。塊匹配三維協同濾波（BM3D）和塊匹配四維協同濾波（BM4D）是一類利用數據局部相似性的算法［11-12］，近年來被用于地震信號恢復，這類算法可用于結構復雜的地震數據重建與去噪。為了獲得一種自適應的稀疏變換基函數，人們提出了多種通過字典學習估計基函數的自適應稀疏變換算法，這類算法能夠自適應地從數據本身派生出模型，從而處理結構復雜的數據。常用的具有代表性的字典學習算法有：①最優方向法［13］，是一種較早提出的字典學習算法，用L0范數計算數據的稀疏性、用交替優化方式求解學習模型；②K奇異值分解（K-singular value decomposition，K-SVD）算法［14-15］，是對K均值算法的拓展，通過字典更新和稀疏編碼兩個步驟的不斷迭代處理數據；③在線字典學習算法［16-17］，通過一次只處理一個樣本并結合最小角回歸算法進行系數編碼獲得更快的字典學習收斂速度，實現大規模樣本的字典學習。此外，還有廣義主成分分析、組結構字典學習等具有代表性的字典學習算法。

上述字典學習算法都對字典的自由度進行一定控制，從而使算法穩定。數據驅動緊框架（datadriven tight frame，DDTF）理論［18］限定學習字典為一組平移不變的冗余小波緊框架，通過進一步控制字典的自由度，使DDTF算法擁有良好的魯棒性，并且利用小波緊框架完美的重構特性，可更好地保留數據的精細特征。

DDTF算法已廣泛用于圖像處理領域，近年來也嘗試處理二維地震數據［19］。本文將DDTF理論擴展到處理三維地震數據，并通過仿真實驗和實際數據處理，對比曲波變換、BM4D和DDTF的三維地震數據去噪與重建效果。數值試算結果表明，DDTF算法在地震數據去噪和重建方面更具優勢。

1 基本原理

應用DDTF算法實現三維地震數據去噪和重建包含兩個主要階段：第一階段是DDTF字典學習階段，以數據驅動的方式獲取地震數據的稀疏表示；第二階段是去噪和插值階段，通過對稀疏系數進行閾值處理實現數據去噪、重建。

1.1 DDTF

定義1 設｛fi｝i∈N∈H，其中｛fi｝i∈N是一個序列，N為自然數集或是自然數集的某一子集，H為希爾伯特（Hilbert）空間，如果存在兩個正常數A、B，且A≤B，有

則稱｛fi｝i∈N是H中的框架，其中A、B為框架的上、下界。當A＝B時，｛fi｝i∈N稱為緊框架。對于緊框架，框架界的值稱為冗余比，若衡量冗余比的界值A＝B＝1，則緊框架是一組正交基，此時｛fi｝i∈N稱為正規化緊框架［20］，即

在緊框架上可以定義濾波器組（字典）矩陣W及其轉置WT

式中：L2（N）表示可測集為N的L2空間；ai為WT中的第i個列向量，｛ai｝為ai的向量集。利用W可以將原始數據變換為系數，利用WT又能把處理過的系數重構為數據。

定義2 小波緊框架是將小波理論和框架理論相結合的產物，小波緊框架是正交小波基的一般變換，即在小波系統中引入冗余性。可測集為R的L2空間L2（R）中的小波框架是由有限母小波Ψ＝｛ψ1，…，ψm｝∈L2（R）集合的平移和放大產生的［21］，即

當X（Ψ）是緊框架時，稱之為小波緊框架。本文使用小波緊框架初始化字典對字典進行限定。

利用DDTF算法的去噪和重建問題可以看作最優化問題，目標函數為

式中：v為系數向量；g為數據向量；λ為拉格朗日常數，用于平衡重構誤差‖v－Wg‖22和稀疏性‖v‖0的權重參數；I為單位矩陣。

通過以下迭代過程得到目標函數。

（1）稀疏編碼階段。固定W，通過經典的稀疏近似問題求解系數向量v

通過硬閾值方法解決上述優化問題［18］。

（2）字典更新階段。固定v，求解W

Cai等［18］推出了上述問題的顯式解，本文省略了推導過程

可以通過SVD法得出S和U

式中：U、S和D分別為將VGT通過SVD算法分解所得的兩個相互正交的矩陣和一個對角矩陣；V＝［v1，v2，…，vN］為gN在W下變換所得系數向量組合而成的矩陣；G＝［g1，g2，…，gN］為矢量形式的樣本組合矩陣。

圖1為DDTF初始字典與訓練字典。由圖可見，對應于初始字典（圖1a），在訓練字典中可以看到明顯的結構性特征（圖1b），故訓練字典能更稀疏地表示原始數據。

1.2 數據分塊與塊聚合

字典訓練的樣本由數據分塊策略獲取，且為了獲取更多的樣本，在分塊時保證塊之間具有一定的重疊度。由數據分塊策略得到的樣本不但可以獲取數據本身的先驗信息，且基于數據塊之間的相似性，在保留數據有效信息的同時去除無用信息。本文將數據分塊后，然后將塊向量化，作為一個列向量得到樣本矩陣（圖2）。數據分塊時使用分塊算子B，塊聚合時使用合成算子BT。若將塊轉換為數據時，把每一個像素除以其重疊度，即可得到原始數據。

圖1 DDTF初始字典（a）與訓練字典（b）

圖2 數據分塊

1.3 去噪與插值算法

從迭代中得到訓練字典W后，采用稀疏促進方法去噪和重建。優化以下目標函數

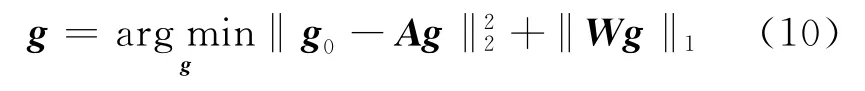
式中：g0為采樣數據；A為采樣矩陣。如果A＝I，上述目標函數表示去噪問題。如果A是一個稀疏采樣矩陣，則上述目標函數表示插值問題。

對于去噪問題，使用單步閾值算法求解

式中Tθ為軟閾值算子，其中θ為閾值參數。

對于插值問題，使用迭代收縮閾值（IST）算法求解

式中參數αk控制算法的穩定性，迭代過程中αk從1減小到0。

1.4 算法實現流程

算法主要包含兩個階段（圖3）。

（1）字典學習，在此階段利用小波緊框架初始化字典，再通過稀疏編碼和字典更新得到訓練后的字典。

（2）去噪或插值，由訓練后的字典得到數據的稀疏表示。若輸入含噪地震數據，則使用單步閾值法處理稀疏系數，得到去噪后數據；若輸入預插值后的欠采樣地震數據，則使用迭代收縮閾值法處理稀疏系數，得到重建數據。

圖3 本文算法流程

2 仿真實驗和實際應用

對于三維地震數據去噪和重建，應用DDTF算法進行仿真實驗，作為算法對比，選用固定基函數的典型稀疏變換方法（曲波變換）和基于塊匹配策略的協同濾波算法（BM4D）處理地震數據。利用三維合成地震數據和三維實際地震數據作為原始數據，原始數據尺寸為128×128×128，字典尺寸和樣本尺寸為8×8×8，并盡量選擇能達到最高信噪比（SNR）的其他參數，利用

初步判斷不同方法的數據處理效果。式中X*和X分別表示原始地震數據及去噪或重建后的地震數據。

2.1 仿真實驗

為了驗證本文算法的可行性和優勢，合成了一個三維地震數據作為仿真實驗模型并驗證處理結果（圖4）。

2.1.1 合成數據去噪

對純凈的三維合成地震數據添加強隨機噪聲后，致使部分有效信號被強噪聲覆蓋，同相軸連續性變差、細節變模糊（圖5）。曲波變換具有多尺度、多方向性質，適用于處理同相軸完整、連續的地震數據。BM4D通過相似匹配獲取數據先驗信息，DDTF通過字典學習獲取數據先驗信息。上述三種算法對含噪數據（圖5）的去噪結果（圖6）中均殘留少量噪聲，整體去噪效果較好，但DDTF的去噪效果更好（圖6c、圖6f），同相軸更完整。

圖4 三維合成地震數據（a）及其局部放大（b）

圖5 對圖4a數據添加20%隨機噪聲（SNR＝14.44dB）

2.1.2 合成數據重建

對圖4a數據隨機剔除50%的地震道得到欠采樣三維合成地震數據（圖7），其同相軸不連續、有效信號缺失嚴重。同樣使用曲波變換、BM4D、DDTF算法對圖7數據的重建結果表明：①整體上三種算法的重建效果較好，較完整地恢復了同相軸。②曲波變換重建效果較好，但是同相軸外的區域產生了少量噪聲，造成同相軸局部扭曲（圖8a、圖8d）；BM4D重建結果中存在同相軸局部輕微錯動（圖8b、圖8e）；DDTF重建結果中同相軸更完整且連續，重建數據的信噪比最高（圖8c、圖8f）。

圖6 合成數據去噪結果及其局部特征

2.2 實際應用

為了驗證DDTF算法的實際應用效果，從新疆A區的三維實際地震數據中截取了尺寸為128×128×128的數據（圖9a）作為含噪數據或欠采樣數據的原始數據，并驗證處理結果。

2.2.1 實際數據去噪

對實際三維地震數據添加20%的隨機噪聲，能量較強的噪聲幾乎將能量較弱的有效信號全部覆蓋，同相軸連續性很差、細節特征丟失嚴重（圖10）。應用曲波變換、BM4D和DDTF三種算法對圖10數據的去噪結果表明：①由于實際地震數據結構更復雜，傳統的固定基函數的曲波變換算法的去噪效果較差，同相軸連續性差（圖11a、圖11d）。因此由固定的模型套用結構復雜的數據是勉強的，須利用數據的先驗信息自適應構建稀疏變換的基函數。②BM4D和DDTF能夠較好地利用數據的先驗信息，去噪效果較好，但是BM4D的去噪結果過于平滑，缺失了數據本身的一些細節特征（圖11b、圖11e）；DDTF的去噪結果更多地保留了原始數據的精細特征，且信噪比更高（圖11c、圖11f）。

圖7 欠采樣合成三維地震數據（SNR＝3.29dB）

圖8 合成數據重建結果及其局部特征

圖9 三維實際地震數據（a）及其局部放大（b）

圖10 對圖9a數據添加20%的隨機噪聲（SNR＝14.56dB）

2.2.2 實際數據重建

對實際三維地震數據隨機剔除50%的地震道得到欠采樣數據（圖12），使用曲波變換、BM4D、DDTF算法對欠采樣數據的重建結果表明：①由于曲波變換固定基函數的局限性，重建結果不理想（圖13a、圖13d）；BM4D的重建結果過于平滑，細節特征缺失嚴重（圖13b、圖13e）；DDTF的重建結果信噪比更高，且盡量保留了原始數據的精細特征，從而驗證了DDTF算法的實用性（圖13c、圖13f）。②曲波變換和BM4D在處理結構更復雜的實際地震數據時，去噪和重建效果較仿真實驗差，但是DDTF去噪和重建效果仍然較好。

2.3 計算效率分析

表1為不同方法的計算時間對比。由表可見，DDTF算法的計算時間是另外兩種算法的幾倍至幾十倍，原因為：一是計算機自身屬性；二是DDTF方法采用字典學習算法，大量的字典訓練量會消耗較多的時間；三是DDTF算法進行數據重建時進行了多重迭代過程，同樣會消耗較多的時間。在實際工作中如果遇到數據量更大的三維地震數據，可以采用并行化算法，或在數據分塊時減少塊之間的重疊，減少訓練樣本數量，從而提高DDTF算法的計算效率。

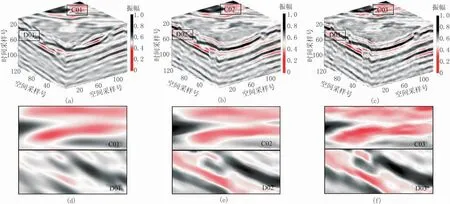
圖11 實際數據去噪結果及其局部特征

圖12 欠采樣實際三維地震數據（SNR＝3.01dB）

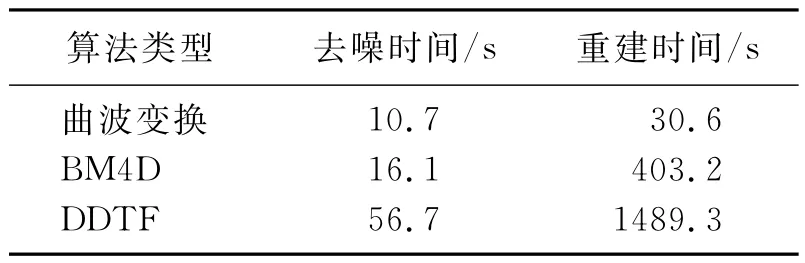
表1 不同方法的計算時間對比

圖13 實際數據重建結果及其局部特征

3 結論

本文基于DDTF理論，研究了三維地震數據去噪和重建問題。DDTF算法通過字典學習，能從數據本身得到最優的稀疏表示，從而適用于結構復雜的地震數據，并且利用小波緊框架完美的重構特性，可以很好地恢復原始數據的精細特征。仿真實驗和實際數據應用結果表明：DDTF算法對結構簡單的三維合成地震數據及結構復雜的實際三維地震數據都具有良好的去噪和重建效果，但計算效率較低，還需進一步改進；曲波變換對實際數據的去噪和重建效果較差；BM4D的去噪和重建結果過于光滑，會丟失一些結構特征。