疊前深度偏移地震記錄直接模擬方法

吳 涵 廉西猛 孫成禹* 芮擁軍 蔡瑞乾 鄧小凡

（①中國(guó)石油大學(xué)（華東）地球科學(xué)與技術(shù)學(xué)院地球物理系，山東青島266580；②中國(guó)石化勝利油田分公司物探研究院，山東東營(yíng)257022）

0 引言

疊前深度偏移是目前油氣地震勘探資料處理中的關(guān)鍵技術(shù)。獲取疊前深度偏移地震記錄要經(jīng)過炮記錄采集或正演、常規(guī)處理和偏移歸位處理等諸多環(huán)節(jié)。而地震正演與偏移成像存在計(jì)算量大、運(yùn)行周期長(zhǎng)等問題，且常規(guī)處理和偏移流程較為繁瑣。為提高正演和偏移的效率，研究人員做了許多工作：王德利等［1］對(duì)黏彈介質(zhì)中三維波動(dòng)方程進(jìn)行了有限差分MPI并行正演及驗(yàn)證；Micikevicius［2］針對(duì)GPU的有限差分實(shí)現(xiàn)給出了快速算法；龍桂華等［3］應(yīng)用GPU實(shí)現(xiàn)了三維地震波交錯(cuò)網(wǎng)格有限差分模擬的加速計(jì)算；李博等［4］、劉守偉等［5］、Foltinek等［6］研究了基于GPU加速的高階有限差分疊前逆時(shí)偏移，取得了顯著的成果；李振華等［7］利用無記憶擬牛頓—模擬退火法對(duì)偏移算子方程進(jìn)行求解，提出了一種正則化偏移成像的全局優(yōu)化快速算法；屠寧［8］對(duì)基于壓縮感知的快速最小二乘逆時(shí)偏移進(jìn)行了研究，降低了最小二乘逆時(shí)偏移中波動(dòng)方程的計(jì)算量。

盡管如此，獲取疊前深度偏移剖面流程繁瑣的根本問題依舊未能得到解決。為簡(jiǎn)化這一復(fù)雜流程、快速獲得偏移剖面，人們往往應(yīng)用一維褶積進(jìn)行偏移剖面的模擬，但對(duì)于二維、三維復(fù)雜速度模型模擬效果不甚理想［9］。Hamran等［10-11］、Gelius等［12-14］、Wu等［15］、Zhu等［16］、朱小三等［17］在廣義散射層析成像的研究中詳細(xì)介紹了波場(chǎng)的成像條件及成像分辨率算子，實(shí)現(xiàn)了高精度的散射層析成像反演；馬在田［18］研究了地震偏移成像分辨率與觀測(cè)系統(tǒng)、成像點(diǎn)、震源等的關(guān)系，給出地震成像分辨率的定量計(jì)算公式，闡述了觀測(cè)地震道的分辨率和成像分辨率的空間變化的特征。

Lecomte等［19-22］分析了疊前深度偏移成像分辨率算子，提出用散射波數(shù)算子表征地震成像分辨率函數(shù)，并以此實(shí)現(xiàn)局部小區(qū)域的疊前深度直接模擬成像。在此基礎(chǔ)上，本文發(fā)展了一種基于深度域廣義卷積技術(shù)的疊前深度偏移地震記錄直接模擬方法，在已知速度模型和野外采集參數(shù)的前提下，無需經(jīng)過波場(chǎng)正演和偏移處理，便可以直接快速生成偏移剖面，得到理論成像結(jié)果。根據(jù)理論成像結(jié)果，可以檢測(cè)觀測(cè)系統(tǒng)的優(yōu)劣和地震數(shù)據(jù)的質(zhì)量，為優(yōu)化觀測(cè)系統(tǒng)參數(shù)和評(píng)價(jià)成像質(zhì)量提供參考，以滿足數(shù)據(jù)采集和處理中質(zhì)量控制的需求［23-25］。

1 方法原理

對(duì)地下介質(zhì)正演和成像過程可以用算子的形式分別表示為

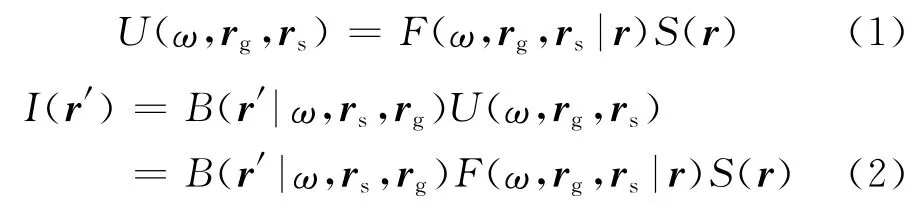
式中：F是模型的正演算子，用于生成模型S的正演數(shù)據(jù)U；B是成像算子，用于生成U的成像結(jié)果I；r表示模型中散射點(diǎn)位置；r′表示模型中散射點(diǎn)成像位置；rg為檢波點(diǎn)位置；rs為震源位置（圖1）。由式（2）可知，通過算子可實(shí)現(xiàn)由模型S直接獲取成像結(jié)果I。

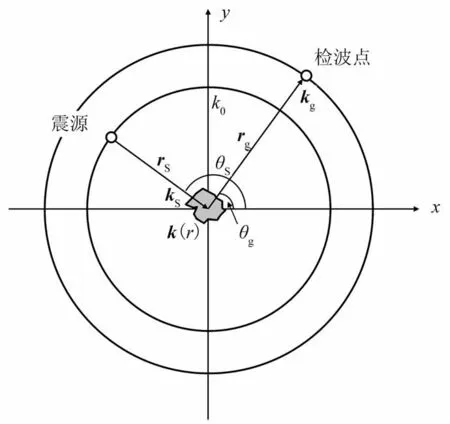
圖1 地震散射波場(chǎng)傳播示意圖

標(biāo)量聲波方程可表示為

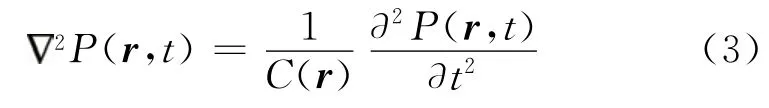
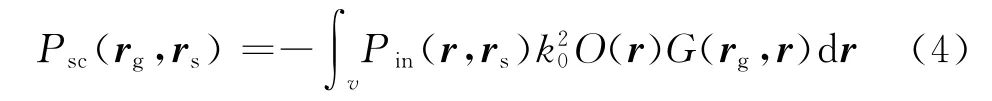
式中：速度擾動(dòng)函數(shù)O（r）一定程度上可近似看作反射率；C0（r）為背景速度場(chǎng)；k0＝ω/C0為背景波數(shù)；Psc、Pin分別代表散射波場(chǎng)和入射波場(chǎng)；v為散射體范圍。對(duì)于一個(gè)非均勻且無衰減的背景場(chǎng)，可以使用動(dòng)態(tài)射線追蹤得到其格林函數(shù)G（rg，r）［26］，結(jié)合Stamnes［27］給出的格林函數(shù)近似解，并引入一個(gè)偏移算子l（rg，rs，r′），則此時(shí)散射點(diǎn)的成像結(jié)果可表示為

式中：D（r，r′）即是直接成像算子，本文將其稱為點(diǎn)擴(kuò)散算子；a和τ為

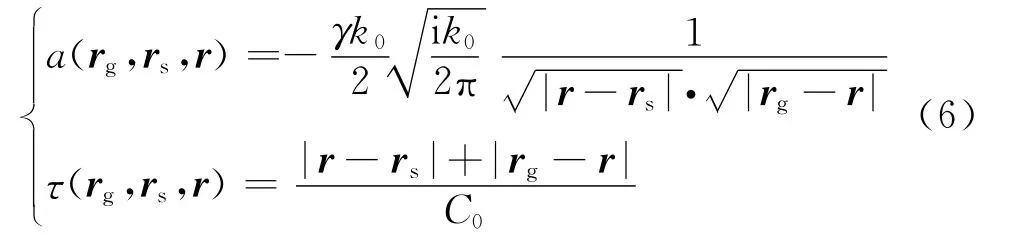
其中γ表征振幅項(xiàng)。

結(jié)合Beylkin等［28-29］提出的理論，在成像點(diǎn)的鄰域內(nèi)將振幅項(xiàng)和相位項(xiàng)Talor展開，結(jié)合程函方程并使點(diǎn)擴(kuò)散算子趨近于δ函數(shù)，同時(shí)為了得到攜帶地震波響應(yīng)的疊前深度偏移剖面，需將地震子波作用在點(diǎn)擴(kuò)散算子上，則有

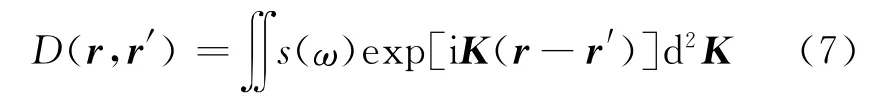
式中：s（ω）為地震子波的頻譜；，其中ks為沿著震源點(diǎn)到成像點(diǎn)的射線路徑上的波數(shù)向量，kg為沿著成像點(diǎn)到檢波器的射線路徑上的波數(shù)向量，且有。由此，可以使用地震子波信息、觀測(cè)系統(tǒng)參數(shù)和射線路徑信息在波數(shù)域構(gòu)建點(diǎn)擴(kuò)散算子，與地下速度模型的速度擾動(dòng)或反射率信息相互作用，即可得到理論成像結(jié)果。同時(shí)，還可以將擾動(dòng)點(diǎn)近似看成是一個(gè)小區(qū)域內(nèi)的照明點(diǎn)，即擾動(dòng)點(diǎn)處的點(diǎn)擴(kuò)散算子可以對(duì)擾動(dòng)點(diǎn)臨近區(qū)域進(jìn)行局部模擬成像。

2 點(diǎn)擴(kuò)散算子分析

由上文可知，將點(diǎn)擴(kuò)散算子與速度擾動(dòng)函數(shù)褶積即可得到模擬成像結(jié)果。速度擾動(dòng)函數(shù)可以近似看作反射率，由地下速度模型直接得出。空間域的褶積運(yùn)算相當(dāng)于波數(shù)域的乘積運(yùn)算，點(diǎn)擴(kuò)散算子可以在波數(shù)域由震源信息、觀測(cè)系統(tǒng)信息及其射線路徑信息構(gòu)建。為說明具體算法和效果，本文以主頻為25Hz的Ricker子波作為震源，起始炮點(diǎn)位置為50m，終止炮點(diǎn)位置為4600m，炮點(diǎn)距為50m，每炮共461道接收，道間距為10m，計(jì)算了Marmousi模型（圖2）中四個(gè)點(diǎn)處的點(diǎn)擴(kuò)散算子（圖3），以此觀察點(diǎn)擴(kuò)散算子的形態(tài)。由圖3可以看出，點(diǎn)擴(kuò)散算子隨著深度的增加，地震波頻譜帶寬變窄、波長(zhǎng)變長(zhǎng)，表明成像分辨率逐漸降低。圖4、圖5展示了（1500m，2000m）附近局部區(qū)域（1000m×1000m）的模擬成像過程，可以看出，在給定速度模型信息、震源信息、觀測(cè)系統(tǒng)信息的情況下，構(gòu)建的點(diǎn)擴(kuò)散算子可以對(duì)地下構(gòu)造進(jìn)行準(zhǔn)確模擬成像。

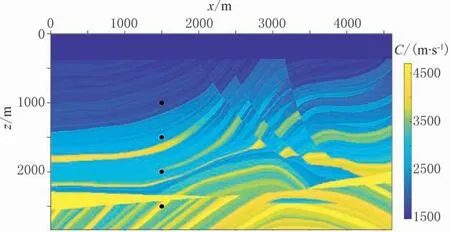
圖2 Marmousi模型及四個(gè)散射點(diǎn)示意圖

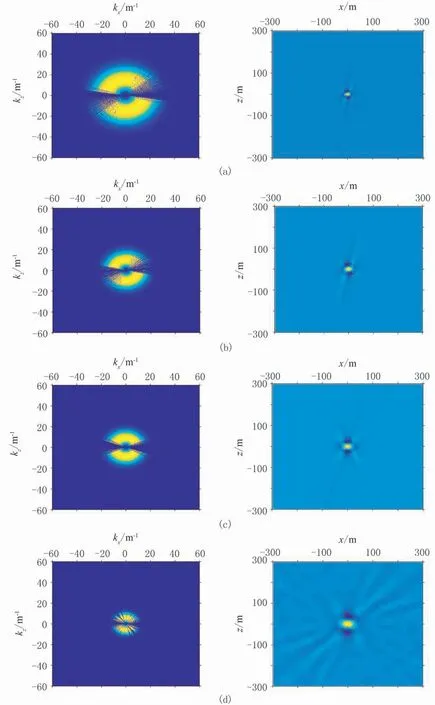
圖3 Marmousi模型不同位置處的波數(shù)（左）和空間（右）域點(diǎn)擴(kuò)散算子

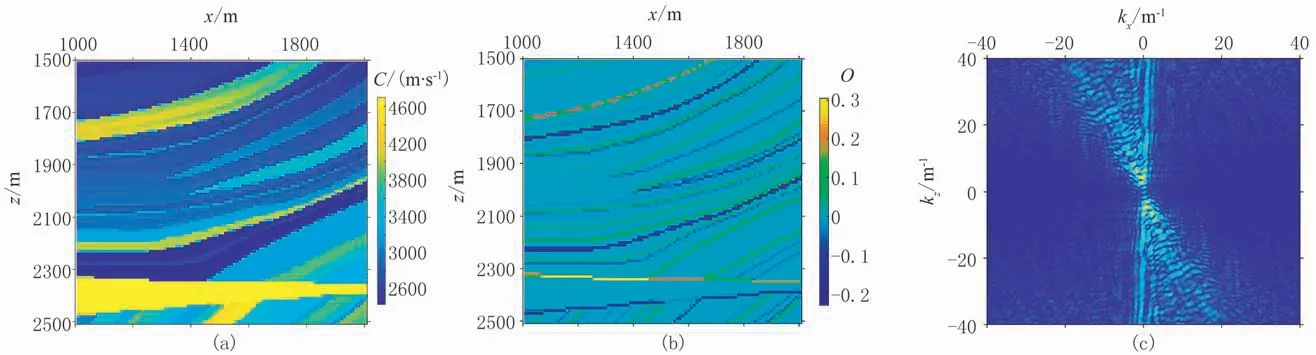
圖4 Marmousi模型（1500m，2000m）附近的速度分布（a）、反射率模型（b）及反射率模型的波數(shù)域振幅譜（c）

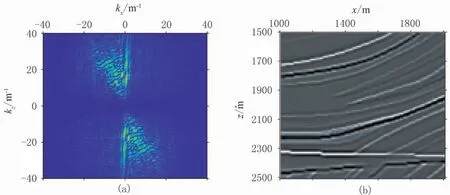
圖5 Marmousi模型（1500m，2000m）附近的直接模擬成像波數(shù)域結(jié)果（a）及空間域結(jié)果（b）

3 模型試算

通過簡(jiǎn)單凹槽模型和Marmousi模型，驗(yàn)證疊前深度偏移地震記錄直接模擬方法的準(zhǔn)確性及其在指導(dǎo)觀測(cè)系統(tǒng)設(shè)計(jì)方面的高效性。

3.1 簡(jiǎn)單凹槽模型

建立圖6所示的凹槽模型，尺寸為200×300個(gè)網(wǎng)格，網(wǎng)格間距Δx＝Δz＝5m。采用主頻為30Hz的Ricker子波作為震源進(jìn)行試算，起始炮點(diǎn)位置為5m，終止炮點(diǎn)位置為1000m，炮點(diǎn)距為50m（共20炮），每炮共200道接收，道間距5m。疊前深度偏移地震記錄直接模擬結(jié)果（圖7）能夠準(zhǔn)確反映地下層位位置、形態(tài)以及對(duì)應(yīng)的波形信息。

3.2 Marmousi模型

為了檢驗(yàn)算法的適用性和準(zhǔn)確性，使用圖2所示的Marmousi速度模型進(jìn)行試算。該模型尺寸為461×284個(gè)網(wǎng)格，網(wǎng)格間距Δx＝Δz＝10m。采用主頻為25Hz的Ricker子波作為震源，起始炮點(diǎn)位置為50m，終止炮點(diǎn)位置為4600m，炮點(diǎn)距為50m（共92炮），每炮共461道接收，道間距為10m。圖8為疊前深度偏移地震記錄直接模擬結(jié)果，能夠準(zhǔn)確反映地下地質(zhì)構(gòu)造信息。與地下反射系數(shù)深度域褶積波形相似度很高（圖9），相關(guān)系數(shù)為0.9494，驗(yàn)證了疊前深度偏移地震記錄直接模擬方法的準(zhǔn)確性。

圖10為相同觀測(cè)參數(shù)下Marmousi模型不同方法的疊前深度偏移結(jié)果（正演數(shù)據(jù)由空間八階、時(shí)間二階的波動(dòng)方程有限差分正演方法計(jì)算）。與圖8對(duì)比可以看出：逆時(shí)偏移成像結(jié)果在深部細(xì)節(jié)上，尤其是深部低速目標(biāo)區(qū)以及中部層狀背斜構(gòu)造處，成像效果較差（圖10a深部方框所示），且淺部存在明顯的噪聲干擾（圖10a淺部方框所示）；最小二乘逆時(shí)偏移能夠?qū)ι畈考?xì)節(jié)進(jìn)行準(zhǔn)確成像，但深部與淺部反射率信息對(duì)應(yīng)性較差（圖10b方框所示）；Kirchhoff偏移在中部層狀背斜構(gòu)造和深部低速層附近的成像效果明顯較差，不能夠完整準(zhǔn)確描述地下真實(shí)構(gòu)造（圖10c方框所示）。由此可見，疊前深度偏移地震記錄直接模擬方法能夠?yàn)槌上褓|(zhì)量提供評(píng)價(jià)的參考標(biāo)準(zhǔn)。

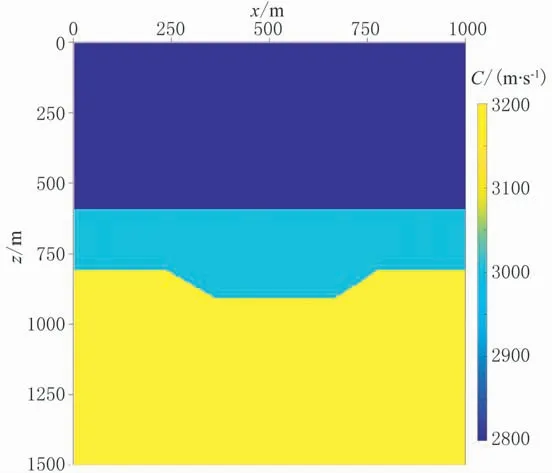
圖6 凹槽速度模型

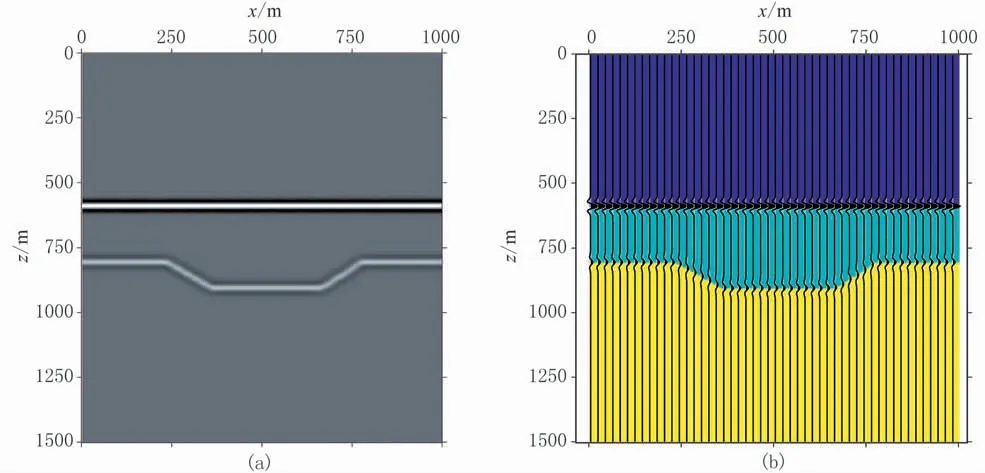
圖7 凹槽模型疊前深度偏移記錄直接模擬結(jié)果（a）及其波形顯示（b）

圖8 Marmousi模型疊前深度偏移地震記錄直接模擬結(jié)果

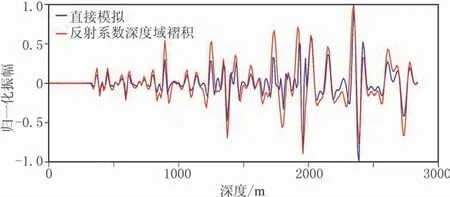
圖9 Marmousi模型直接模擬結(jié)果第200道歸一化波形與反射系數(shù)深度域褶積的對(duì)比

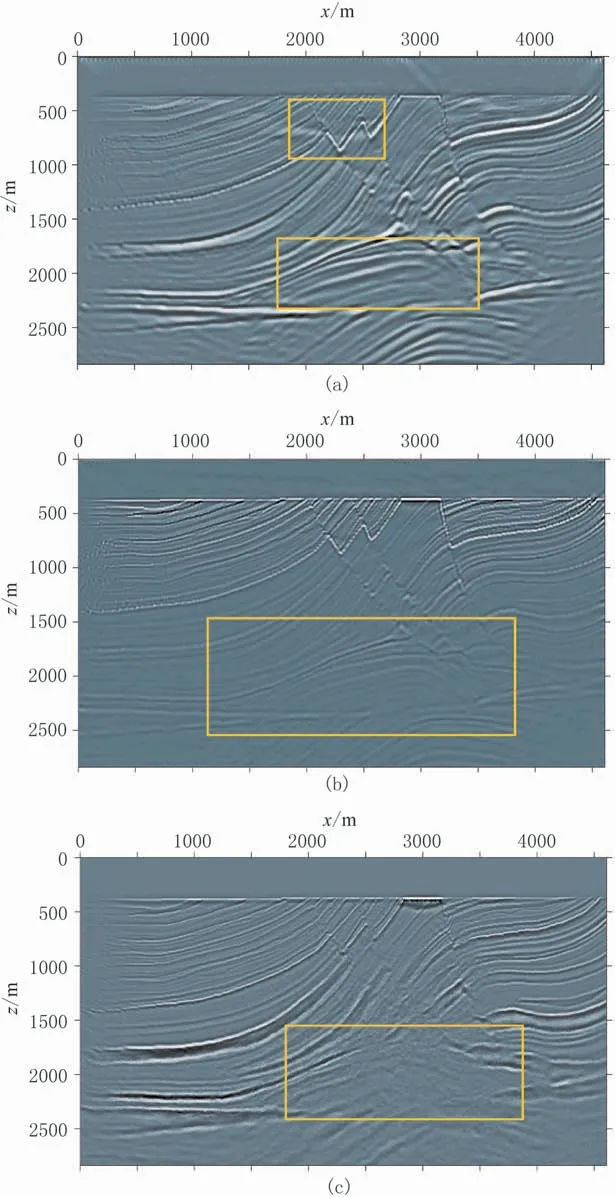
圖10 不同疊前深度偏移方法成像結(jié)果對(duì)比

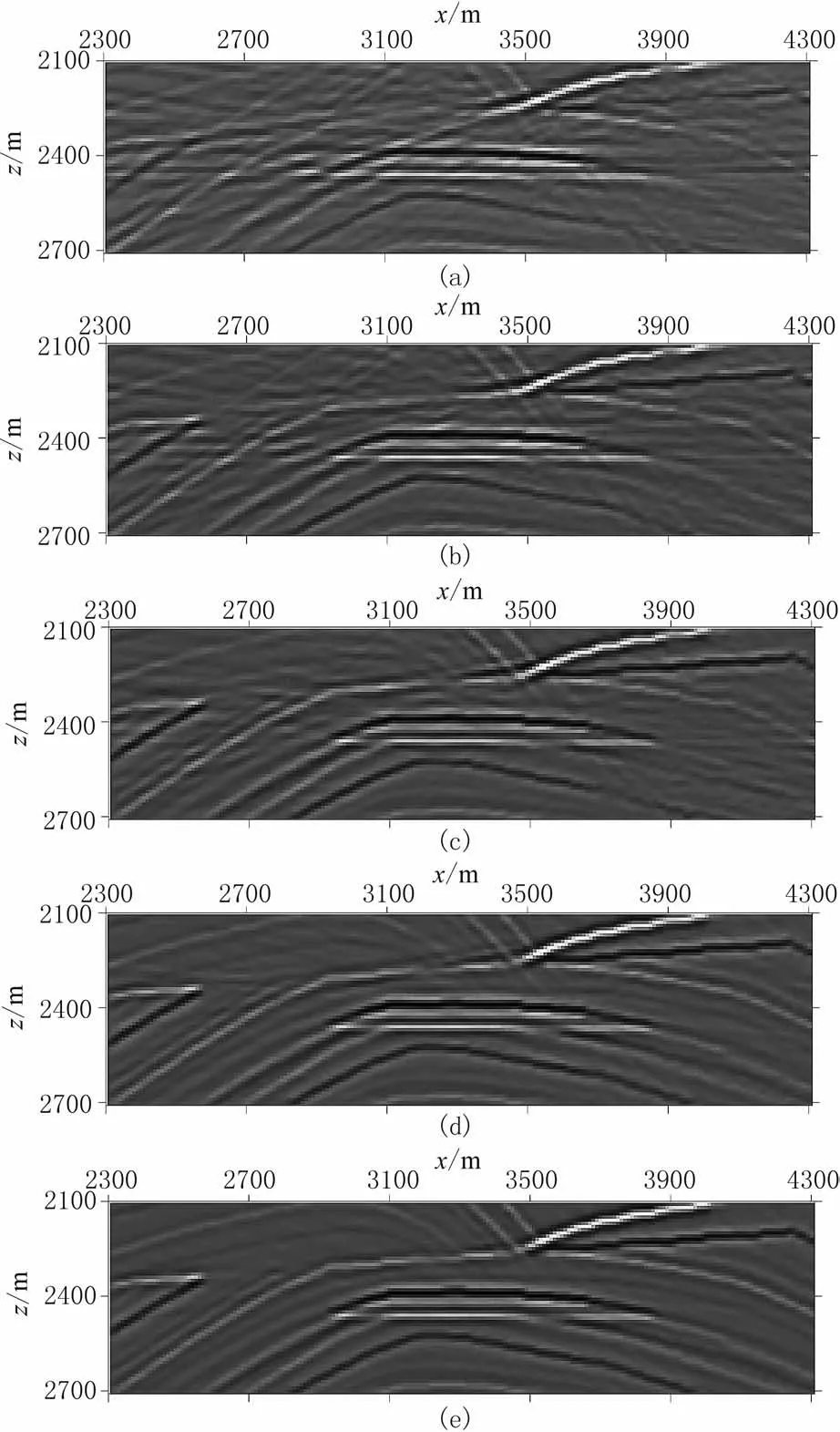
圖11 Marmousi模型不同炮點(diǎn)距低速目標(biāo)層模擬成像結(jié)果

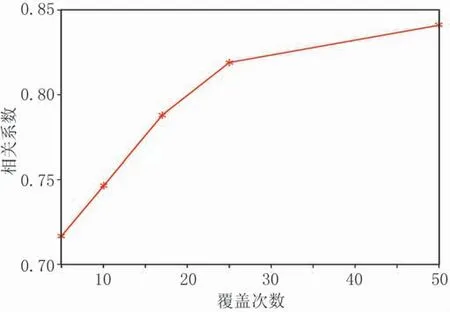
圖12 Marmousi模型不同覆蓋次數(shù)模擬成像剖面第340道與對(duì)應(yīng)反射系數(shù)深度域褶積的波形相關(guān)性分析

采用主頻為25Hz的Ricker子波作為震源，起始炮點(diǎn)位置為0，炮點(diǎn)距分別為100、50、30、20、10m，炮點(diǎn)右側(cè)接收，最小炮檢距為10m，最大炮檢距為1000m，道間距為10m，共100道接收，計(jì)算不同覆蓋次數(shù)（分別為5、10、17、25、50）的直接模擬成像結(jié)果。圖11展示了不同觀測(cè)系統(tǒng)參數(shù)下Marmousi模型深度2500m附近低速目標(biāo)區(qū)域疊前深度偏移地震記錄直接模擬結(jié)果，覆蓋次數(shù)越高的觀測(cè)系統(tǒng)成像效果越好。炮點(diǎn)距為20m（覆蓋次數(shù)為25）時(shí)成像準(zhǔn)確（圖11d），成像剖面第340道波形與對(duì)應(yīng)反射系數(shù)深度域褶積波形相關(guān)系數(shù)為0.8190（圖12）；炮點(diǎn)距為30m（覆蓋次數(shù)為17）時(shí)成像結(jié)果（圖11c）也可識(shí)別出目標(biāo)層及其附近構(gòu)造，第340道波形與對(duì)應(yīng)反射系數(shù)深度域褶積波形相關(guān)系數(shù)為0.7878（圖12）。兼顧經(jīng)濟(jì)、效率兩方面要求，建議采用20～30m的炮點(diǎn)距進(jìn)行地震采集。

4 結(jié)束語

本文研究了一種在已知速度模型和野外采集參數(shù)的前提下直接模擬疊前深度偏移記錄的方法。該方法可以簡(jiǎn)單高效地獲得疊前深度偏移的理論成像結(jié)果，省去了繁瑣的炮記錄正演、常規(guī)處理及偏移等一系列過程。其模擬成像精度能夠準(zhǔn)確反映地質(zhì)構(gòu)造信息及反射率信息，可為評(píng)價(jià)觀測(cè)系統(tǒng)和成像質(zhì)量提供參考標(biāo)準(zhǔn)，以滿足采集觀測(cè)系統(tǒng)設(shè)計(jì)、成像處理和儲(chǔ)層分析等領(lǐng)域的研究需求。