傾斜檢波器與地表雙自由度耦合效應
孫 超,孫 亮,何登科,田思清
(1.山東省煤田地質規劃勘察研究院,山東 濟南 251000;2.中國礦業大學(北京) 煤炭資源與安全開采國家重點實驗室,北京 100083)
地震數據采集過程中,檢波器用于感知地表介質的運動狀態。檢波器與地表介質相互作用形成耦合系統,在頻率域表現為特定的濾波器。該濾波器對不同頻帶的地震信號產生不同的壓制或放大作用,導致原始地震信號畸變。因此,檢波器與地表耦合系統直接影響地震信號的品質[1-4]。
H.Washburn 等[5]通過實驗揭示了檢波器與地表形成的耦合系統會影響地震信號的振幅與相位。A.Wolf[6]從理論角度證明檢波器與地表耦合系統可以用阻尼振動系統進行描述。李之權[7]討論了數字檢波器的非線性失真問題。C.E.Krohn[8]通過實驗揭示了耦合系統對低于諧振頻率的信號具有較好的信號還原能力,而對高于諧振頻率的信號造成相位和振幅畸變。徐錦璽等[9]通過實驗表明適當增加檢波器尾椎長度能夠拓寬地震的有效頻帶,有利于高頻信號的采集和保真性。董世學等[10]分析了檢波器地表耦合系統對地震信號的影響,認為需要對地震信號進行校正,改善地震信號的信噪比。呂公河[11]研究認為檢波器對地震波的接收本質上是振動問題,利用振動理論進行分析,可以提高對檢波器接收機理的認識,有利于發展地震信號的接收和激發技術。劉志田等[12]基于振動力學理論提出了檢波器與地表雙自由度耦合系統模型。石戰結等[13-14]提出了檢波器-耦合介質-灰巖的三自由度耦合系統模型,通過野外實驗對比了雙自由度和三自由度耦合系統模型的地震信號響應特征。魏繼東[15]指出檢波器與地表耦合很好地固結時,可以用單自由度耦合模型描述檢波器與地表耦合系統。
何登科等[16]和Sun Liang 等[17]指出煤田地震數據采集過程中,存在同一檢波點位置重復插拔布設檢波器的情況,檢波器多次插拔布設存在傾角差異,影響檢波器與地表耦合效應。針對這一問題,筆者將檢波器傾角參數引入“雙自由度系統”,從振動力學的角度推導傾斜檢波器“雙自由度耦合振動系統”,分析檢波器傾角、相對阻尼系數、地表介質參數對耦合系統的影響。
1 檢波器與地表雙自由度耦合系統運動方程
利用振動力學研究檢波器與地表耦合問題時,地表介質只具有彈性特征,不具有慣性(無質量);檢波器只具有慣性(有質量),不具有彈性特征。地震波在經地表介質傳播至檢波器尾椎過程中,忽略因檢波器與地表介質之間摩擦而造成的能量消耗[12-13]。許多學者[2,12,14]認為地震信號經檢波器尾椎傳播至檢波器機芯過程中,將存在2 個振動系統:檢波器芯體的振動和檢波器尾椎相對于地表的振動,即“雙自由度系統”。當某一檢波點位置初次布設檢波器時,由于地表介質固結較好,檢波器與地表耦合響應滿足“雙自由度系統”。
由于人為和外界因素影響,檢波器在實際埋置過程中產生傾斜,因此,將檢波器傾角引入“雙自由度耦合振動系統”。圖1a 為傾斜檢波器,其表示小角度傾斜的檢波器被埋置于地表介質中。圖1b 為檢波器傾斜情況下的雙自由度耦合系統模型,mg為檢波器芯體內慣性體(線圈架及線圈)的質量,kg為檢波器內部的彈簧剛度,dg為檢波器內部的阻尼系數;mc為檢波器尾椎和外殼的總質量,kc為地表介質的剛度,dc為檢波器尾椎與地表介質的阻尼系數;y為地震波傳播至地表引起的垂向振動位移,yc為mc垂直方向振動位移,yg為檢波器內部慣性體mg的垂直方向振動位移;θ為耦合模型傾角(角度以垂直方向為零度)。
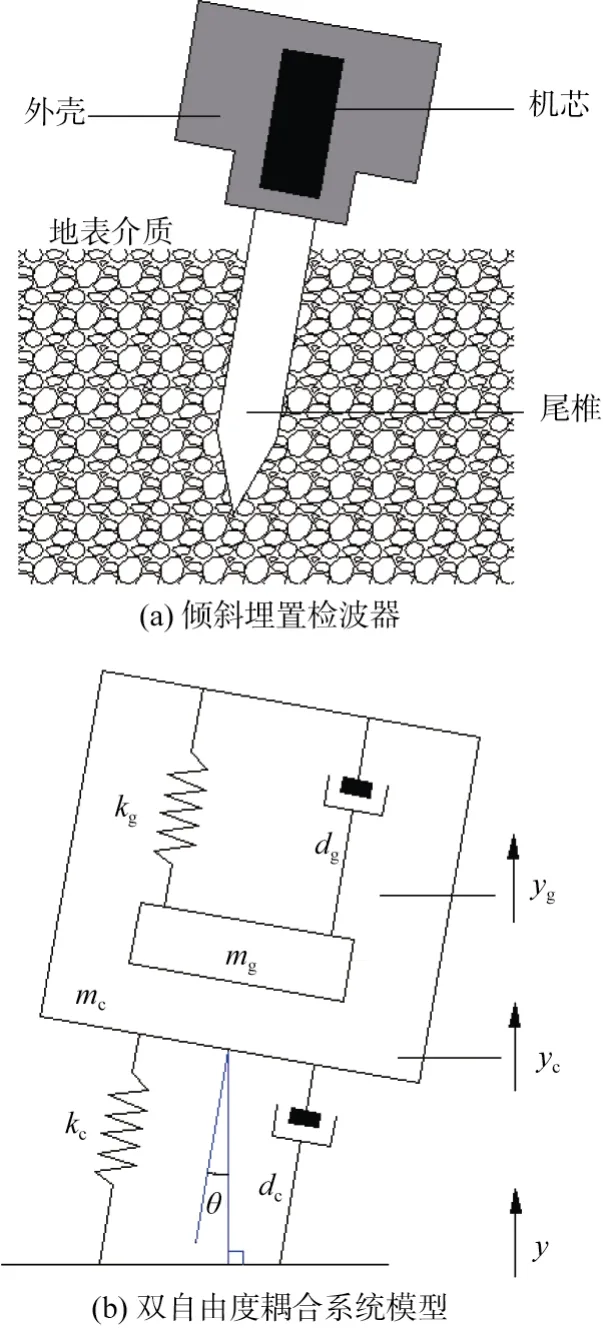
圖1 傾斜檢波器與地表耦合模型Fig.1 Coupling model of the tilt geophones and the surface
若將檢波器作為一個整體,雙自由度耦合系統滿足牛頓第二定律[2,14]:

其中,t表示位移時間。地震波傳播至地表引起的垂向振動y與檢波器最終檢測到的輸出振動之間的比值,即振動傳輸函數H(f):

式中:f為檢波器的激勵頻率;fg為檢波器固有頻率(自然頻率);fc為檢波器尾椎與地表耦合系統的諧振頻率;ξg表示為檢波器芯體內部的相對阻尼系數;ξc為檢波器尾椎與地表耦合系統(“尾耦系統”)的相對阻尼系數。
2 檢波器與地表雙自由度耦合系統響應分析
基于式(10)的傾斜檢波器與地表雙自由度耦合系統的傳輸函數,分析檢波器傾角、地表物性參數和阻尼系數對地震信號振幅、頻率和相位的影響。結合檢波器與地表耦合情況,這里引入一個較為簡單的檢波器地表耦合模型,把檢波器尾椎抽象為圓柱體,檢波器尾椎埋置于地表介質[13]。
檢波器尾椎與檢波器外殼質量mc可以通過式(8)獲得。

式中:gρ為檢波器尾椎的密度;cR為檢波器尾椎的半徑;h為檢波器尾椎高度;mk為檢波器外殼的質量。
設地表介質的彈性系數為ks,地表介質與檢波器尾椎的接觸彈性系數為kcs,基于彈簧串聯計算公式[18],那么檢波器與地表介質的剛度系數kc為:

基于文獻[19],可以得到地表介質的剛度和接觸剛度系數為:
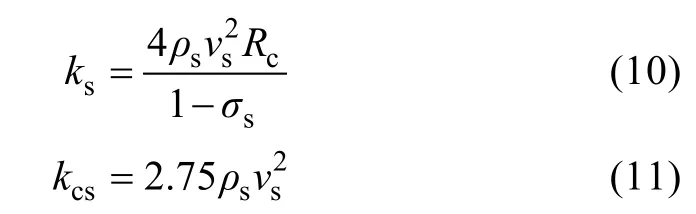
利用地表介質物性參數和檢波器尾椎參數(表1),地表介質物性參數、耦合介質物性參數和檢波器尾椎的基本參數引用前人實驗測試結果[20-21]。檢波器與地表雙自由度耦合系統中“尾耦系統”的相對阻尼系數與地表介質的內阻尼、檢波器尾椎材料、尾椎與地表介質的接觸阻尼和空氣阻尼等有關。在理論上計算阻尼系數十分困難,一般采用實驗測試進行確定;在數值模擬過程中,檢波器與地表雙自由度耦合系統中“尾耦系統”的相對阻尼系數取0.2。檢波器參數為:mg=0.011 3 kg,kg=45 N/m,ξg=0.6,mk=0.01 kg。

表1 表土和檢波器尾椎參數Table 1 Parameters of the surface soil and the geophone spike
2.1 檢波器傾角對耦合系統的影響
當檢波器分別傾斜0o、15o、30o、45o時,檢波器-地表介質耦合系統的幅頻、相頻響應分別如圖2a 和2b 所示。圖2a 中曲線表明:檢波器-地表耦合系統的2 個諧振頻率分別為檢波器芯體的諧振頻率(10 Hz)和檢波器尾椎-地表耦合系統的諧振頻率(180 Hz 附近)。檢波器傾角對檢波器芯體振動的諧振頻率和振幅響應沒有明顯影響;隨著傾角的增加,檢波器尾椎-地表耦合系統的諧振頻率提高,并且導致各頻段的振幅能量減小。當頻率分布在0~10 Hz,檢波器-地表耦合系統的振幅譜值小于1,該頻段地震信號的振幅能量將被衰減;當頻率分布在10~50 Hz,隨著檢波器傾斜角度的增加,振幅譜能量衰減,導致檢波器-地表耦合系統的振幅譜值略小于1,有效地震信號基本分布在該頻段,因此,有效信號的振幅能量會有一定的衰減;當頻率分布大于50 Hz,檢波器-地表耦合系統的振幅譜值不斷增加,將對該頻段地震信號的振幅產生明顯影響,因此,增強了高頻地震信號的影響,地震信號的信噪比將降低。從圖2b 中的曲線可知:檢波器-地表雙自由度耦合系統具有2 個相位躍變點,分別對應檢波器芯體的諧振頻率(10 Hz)和檢波器尾椎-地表耦合系統的諧振頻率(200 Hz 附近)。檢波器-地表耦合系統將引起相位的躍變,對地震信號的接收時間產生一定影響。

圖2 傾角對耦合系統的影響Fig.2 The influence of tilt angle on coupling system
圖3 表示地震信號通過傾斜檢波器-地表耦合系統的波形差異,由圖中可知,地震信號在通過具有不同傾角的檢波器-地表耦合系統后波形的振幅能量變化較小。結合圖2 可知:檢波器傾角的增加使得幅頻響應減小,檢波器接收的地震信號的振幅能量將減小;相頻響應變化較小,因此相位變化較小,檢波器接收的地震信號的波形與實際地震信號的波形基本沒有差別。因此,檢波器傾角的變化對地震信號的影響主要表現為振幅能量的差異,波形特征基本沒有變化。

圖3 傾角對地震信號的影響Fig.3 The influence of tilt angle on seismic signal
2.2 阻尼系數對耦合系統的影響
圖4a 和圖4b 為“尾耦系統”的相對阻尼系數分別取值為0.2、0.5、1.0 時,檢波器與地表雙自由度耦合系統的幅頻、相頻響應。圖4a 表明:阻尼系數增加對雙自由度耦合系統的諧振頻率影響較小,檢波器芯體振動的諧振頻率和檢波器尾椎相對于地表介質振動的諧振頻率均沒有發生變化,阻尼系數的增加,導致檢波器與地表耦合系統的幅頻響應減小,幅頻響應曲線線性明顯增強。當ξc=1 時,幅頻響應曲線趨近于線性特征,幅頻響應趨近于1,雙自由度耦合系統對地震信號的影響減小;當ξc減小時,幅頻響應曲線的非線性增強,且會在一定的頻帶內存在振幅響應峰值,導致耦合系統對高頻地震信號的響應增強。
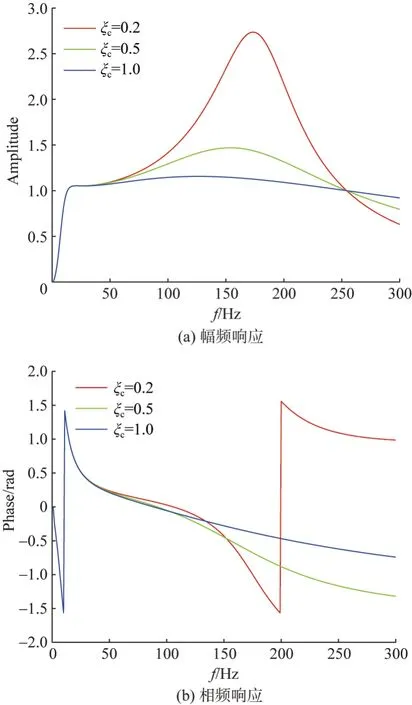
圖4 阻尼系數對耦合系統的影響Fig.4 The influence of damping coefficient on the coupling system
圖4b 可知:阻尼系數的變化對相頻響應曲線影響明顯,阻尼系數的增加會引起相頻響應曲線的線性增強;f>10 Hz 相頻響應趨于零,雙自由度耦合系統對地震信號的相位影響減小。因此,布設檢波器可以通過增加檢波器尾椎與地表介質之間的阻尼系數,提高地震數據的品質。
圖5 為地震信號通過不同阻尼系數的雙自由度耦合系統的波形變化。由圖中可知,地震信號在通過不同阻尼系數的雙自由度耦合系統后波形、振幅能量變化較小。結合圖4 分析,雙自由度耦合系統在f>100 Hz 才表現出明顯的幅頻響應增加和相位畸變。地震信號頻帶在小于100 Hz 時,幅頻響應較弱,地震信號波形的振幅能量變化較小。當ξc增大時,雙自由度耦合系統的幅頻響應和相頻響應線性增強,幅頻響應趨近于1,相頻響應趨近于0。因此,雙自由度耦合系統對地震信號的影響減小。

圖5 阻尼系數對地震信號的影響Fig.5 The influence of damping coefficient on seismic signal.
2.3 地表介質參數和耦合介質參數對耦合系統的影響
圖6a 和圖 6b 為地表介質彈性模量分別取Es=1.0×107、Es=1.2×107、Es=1.4×107時,檢波器與地表雙自由度耦合系統的幅頻、相頻響應。圖6a 表明:檢波器與地表雙自由度耦合系統是具有2 個諧振頻率的諧振系統。隨著彈性模量的增加,檢波器尾椎相對于地表介質的諧振頻率提高。由圖6b 可知:檢波器與地表耦合系統具有2 個相位躍變點,分別對應檢波器芯體的諧振頻率(10 Hz)和檢波器尾椎相對地表介質振動的諧振頻率(190 Hz 附近)。隨著彈性模量的提高,檢波器尾椎相對于地表介質的諧振頻率增加。因此,相位躍變點向后移動。
圖7 為地震信號通過具有不同彈性模量的雙自由度耦合系統的波形變化,由圖中可知,地震信號在通過不同地表介質彈性模量的雙自由度耦合系統后,波形、振幅能量變化較小。結合圖6 分析,地表介質彈性模量的增加使得檢波器與地表雙自由度耦合系統的諧振頻率不斷提高,耦合系統對地震信號的影響將減小。此外,相頻響應變化也較小,進一步減小了相位畸變對地震信號的影響。因此,雙自由度耦合系統條件下,地表介質彈性模量的增加可以減小耦合系統對地震信號的影響,提高地震信號品質。
3 結論

圖6 彈性模量對耦合系統的影響Fig.6 The influence of elastic modulus on the coupling system

圖7 彈性模量對地震信號的影響Fig.7 The influence of the elastic modulus on the seismic signals.
a.檢波器傾斜角度的增加將減弱耦合系統對地震信號的幅頻響應,提高耦合系統的諧振頻率。隨著檢波器傾角的增加,耦合系統對地震響應的影響更顯著,主要體現在振幅的衰減。因此,地震數據采集過程中應盡量保持檢波器趨近于垂直地表。相較于相對阻尼系數和地表介質彈性模量,檢波器傾角對地震信號振幅的影響較大。
b.隨著相對阻尼系數的增大,檢波器-地表耦合系統的幅頻響應趨近于1,諧振頻率變化較小。因此,地震數據采集過程中應盡量增加檢波器與地表之間的相對阻尼,提高地震數據的品質。
c.地表介質彈性模量的增大將導致檢波器-地表耦合系統的諧振頻率提高,但幅頻響應特征變化較小,對地震數據的影響較小。
d.本次以雙自由度耦合系統理論為基礎,建立了傾斜檢波器與地表耦合模型,該模型不適用于灰巖裸露區地震數據采集。下一步可開展三自由度耦合系統理論研究,對比分析2 種耦合模型的幅頻響應差異,拓展模型適用范圍。
請聽作者語音介紹創新技術成果等信息,歡迎與作者進行交流

OSID 碼

