基于ARIMA模型的中國豬肉價格預測

安徽財經大學 張瑩瑩

1 背景

近年來，中國人均對豬肉的消費占比始終在75%以上。盡管我國對牛羊肉等替代產品肉類的消費有所上升，但中國居民人均對牛羊肉的消費始終不及豬肉的1/4。鑒于豬肉消費的重要性，豬肉價格變動一直是生產者和消費者密切關注的重點，豬肉市場的供給情況也是農業部門重點監控對象。自2007年起，豬肉價格開始劇烈波動，豬肉價格的漲跌更替對市場的影響是直接且劇烈的。豬肉價格頻繁的漲跌對生豬養殖產業帶來極大的挑戰。當豬肉供大于求時，豬肉過剩，價格下跌，使養殖戶承受了巨大的經濟損失；當豬肉供不應求時，短期內會使豬肉市場發生膨脹，豬肉價格快速上漲，養殖戶獲得暴利后會擴大養殖規模。

針對豬肉價格波動趨勢的研究，曙光等(2008)采用譜分析的方法測定北京市豬肉價格的季節波動情形，并通過Tukey-Hanning窗譜估計法來預估長期豬肉價格波動，其認為豬肉價格將圍繞31個月形成周期波動。同是研究北京市豬肉價格波動規律，于少東(2012)利用X12季節調整法和H-P濾波法對豬肉價格月度數據進行分析，得出北京市豬肉價格短期內波動劇烈，長期波動周期可能是3年的結論。夏海峰(2016)利用數據挖掘中的關聯規則理念，在去除異常數據以后，結合二維時間序列對每日的豬肉價格進行預測，預測精度達到89.33%。郭剛奇(2017)基于ARCH模型探究短期市場的豬肉價格波動機制，并總結豬肉價格波動的特征之一就是簇集性明顯，短期內豬肉價格極易受外部沖擊如疫病等的影響。李子涵等(2019)收集2010年1月—2019年2月的上海市豬肉價格數據，建立ARIMA(p，d，q)模型對未來5個月的豬肉價格進行預測，得出豬肉價格仍將小幅度上漲的結論。羅創國、吳靜婷在ARIMA模型的基礎上對中國生豬價格以及有代表性的畜產品進行預測，均取得較好的效果。經過對傳統ARIMA模型加以改善，吳培(2019)選擇運用ARIMA-GM-RBF組合模型對中國豬肉價格進行預測，對每個單一模型進行優缺互補，最后在2011—2018年數據的基礎上預測2019年上半年豬肉價格將繼續上漲。綜上所述，國內學者對豬肉價格的研究取得了不菲的成果。他們對豬肉價格的研究所選取的時間跨度不盡相同，分別對每日、每月、每季度的豬肉價格進行研究，考慮到豬肉價格受到外部因素沖擊的影響力度較大，主要進行短期內的豬肉價格預測。豬肉價格的波動不僅影響著豬肉產業鏈的健康發展，也對人民生產生活和整體經濟運行產生重要影響。因此如何準確地預測豬肉價格的波動趨勢，是本文研究的重點。基于此，本文將建立ARIMA(p，d，q)模型的豬肉價格預測，通過對豬肉價格的合理預測為市場各經濟主體提供有效的理論指導，同時減少對生豬養殖戶造成的收益損失，為市場上豬肉價格的宏觀調控提供借鑒和參考。

2 ARIMA模型

1970年，博克思和詹金斯提出了一種時間序列預測方法，即差分自回歸滑動平均模型又稱ARIMA模型。該算法的工作原理是通過多次差分使非平穩序列轉變為白噪聲序列，充分運用變量的歷史信息尋求變化規律，以達到準確預測的目標。該模型多用于農產品和畜產品的價格預測，且實現效果良好。

ARIMA模型構建的基礎是ARMA模型，一般形式為ARMA(p，q)模型：

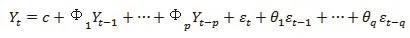
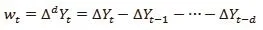
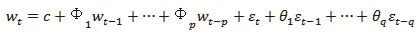
原ARMA(p，q)模型是非平穩時間序列，在d階差分后變為平穩，即ARIMA(p，d，q)模型。ARIMA模型將預測對象隨時間的變化而形成數據流視為隨機序列，通過該模型就可以利用隨機序列的歷史值來預測未來值。

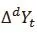
3 基于ARIMA模型的實證分析

本文選取中華人民共和國農業農村部2013年1月—2019年5月的中國豬肉、羊肉和牛肉價格月度時間序列數據，并通過Eviews9.0軟件完成模型計算。近年來，我國豬肉平均價格波動較大，呈現出“跌—漲—跌—漲”的趨勢，波動大致呈現出“W”的形狀，豬肉價格波動趨勢圖，如圖1所示。

為消除原數據異方差性對模型的建立造成影響，需要對豬肉價格提取自然對數。

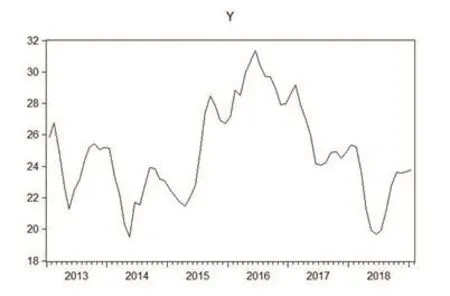
圖1 我國豬肉價格時序圖

為了更好地優化模型，做到更精準的預測，可以適當增加模型的滯后長度，并根據赤池信息準則確定最終設置的模型，結果如表1所示。

由表1可知，根據AIC和SC信息值，本文選擇p=3、q=2建立最終的模型ARIMA(3，1，2)。

對預先設定的ARIMA模型采用線性最小二乘法預測，預測點數為3，得到的豬肉價格如表2所示。

其中，絕對誤差=實際值－預測值，相對誤差=絕對誤差/預測值。由表2計算可得，平均絕對誤差為－1.68，平均相對誤差為－0.54%，預測精度良好，可以接受。

表1 ARIMA模型的赤池信息準則

表2 ARIMA(0，1，1)模型預測結果

對于誤差均方根RMSE，如式(1)所示。

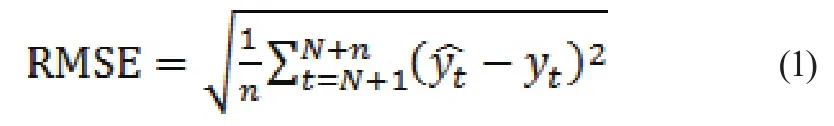
模型中RMSE=0.03，說明觀測值與真實值之間離散程度較小。

為了避免誤差之間可能存在相互抵消的現象，以及更加準確的反映實際值與預測值誤差的大小，選用絕對誤差平均(MAE)指標進行衡量，如式(2)所示。

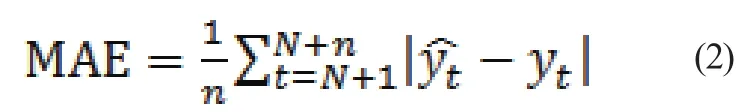
在本文中，絕對誤差平均指數測值為0.03，進一步證明了模型數據之間的離散程度較低，在一定程度上避免了誤差間的互相抵消。

為進一步檢測模型擬合效果，選用Theil不等系數進行評判，即

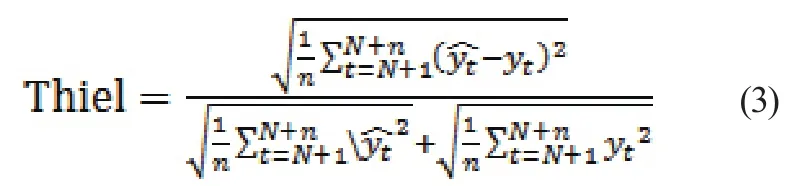
ARIMA(3，1，2)模型的Thiel指數值算出得0.47，取值在0～1且更接近零值，說明擬合程度不錯，預測效果較好。

誤差均方根、絕對誤差平均以及Theil不等系數指標的數值均證明構建的ARIMA(3，1，2)模型，預測結果如圖2所示。 Static預測結果理想，具有準確的精度，可以在實際生產生活中進行運用。

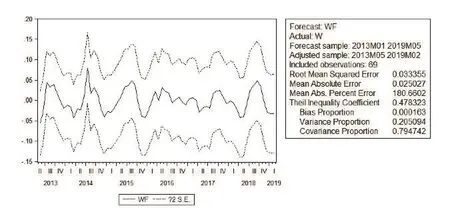
圖2 Static預測結果圖

4 結語

本文首先分析整理大量數據，對近年來我國居民人均肉類消費數量及結構進行分析，發現豬肉基本壟斷我國肉類市場。在豬肉市場份額占比減少時，其替代產品如牛肉、羊肉等其他肉質產品的市場占比就會增加。

繼而以2013年1月—2019年1月的全國豬肉平均價格月度數據為基礎，建立ARIMA(3，1，2)模型進行預測分析，得出的結果是2019年2—4月我國每公斤豬肉平均價格分別為29.92元、37.63元、40.09元。預測結果普遍比真實值要大，但是模型的精度較好，預測出短期內豬肉價格波動呈現上漲趨勢，符合客觀事實。

由于ARIMA模型的被解釋變量為滯后變量，非常適合進行價格的預測。本文所建立的ARIMA(p，d，q)一般模型可以便于價格信息使用者快速、簡便地掌握價格變動趨勢，不僅適用于對豬肉價格的預測，還適用于其他肉質產品及農業產品的價格預測，具有較強普適性。