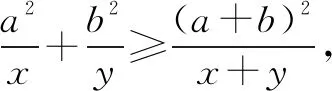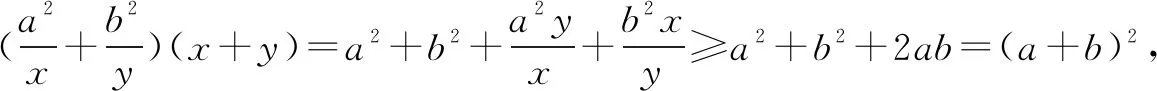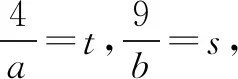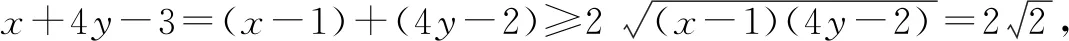對(duì)比習(xí)題研模式 統(tǒng)一解法促效能
——以不等式求解為例
李秀元
(湖北省武穴市實(shí)驗(yàn)高級(jí)中學(xué) 435400)
數(shù)學(xué)是一門尋求“完美”模式的學(xué)問.數(shù)學(xué)解題一般都是有模式的.研究解題模式,熟練運(yùn)用模式解題,對(duì)提高數(shù)學(xué)學(xué)習(xí)成績的現(xiàn)實(shí)意義是積極的.而且,研究解題模式,對(duì)于理解不同題目的關(guān)系,快速解題也是非常有好處的.下面基于不等式問題,舉例說明統(tǒng)一求解模式在不同題目中的應(yīng)用,借此彰顯統(tǒng)一解題模式的積極意義.
一、統(tǒng)一模式,加深對(duì)問題的理解

(2)已知-1 分析對(duì)于問題(1),由于a,b單獨(dú)變化,互不影響,可直接利用不等式的性質(zhì)求解.求解問題(2)時(shí),學(xué)生往往受問題(1)的影響,總是先求a,b的取值范圍,再求2a+3b的范圍.事實(shí)上,a和b在變化過程中是相互制約的,因此不能單獨(dú)確定a和b各自的取值范圍.如果對(duì)a+b和a-b分別換元后,則問題(2)可以回歸到問題(1)的模式. 評(píng)析問題(2)是學(xué)生最易出錯(cuò)的一道題,人教A版課標(biāo)實(shí)驗(yàn)教科書必修5,用一個(gè)“閱讀與思考”來解釋,為什么正確應(yīng)用不等式性質(zhì)的求解,結(jié)果卻是多樣的、錯(cuò)誤的.應(yīng)用模式化方法,使新問題回歸到已有模型,復(fù)雜問題簡單化,求解不會(huì)出現(xiàn)偏差,也根本不需要任何解釋.轉(zhuǎn)化為問題(1)的模型,本質(zhì)上是用a+b和a-b這兩個(gè)整體變量來表示2a+3b,不破壞單獨(dú)變量a和b之間的依賴性,然后借助不等式的性質(zhì),確定其取值范圍. 例2(1)已知f(x)=(ax-1)(x+b),如果f(x)>0的解集為(-1,3),求f(-2x+3)<0的解集; (2)若不等式ax2+bx+c>0的解集為{x|-1 分析對(duì)于問題(1),一般先根據(jù)函數(shù)結(jié)構(gòu),和不等式解的形式,確定函數(shù)類型,求出參數(shù)a和b的值,進(jìn)而解一個(gè)基于f(x)的更復(fù)雜不等式.但這樣求解無視結(jié)構(gòu)特點(diǎn),毫無靈性,無法提高解題的速度和準(zhǔn)確度. 所以不等式a(x2+1)+b(x-1)+c>2ax的解集為(0,3). 方法2:不等式a(x2+1)+b(x-1)+c>2ax可化為a(x-1)2+b(x-1)+c>0,由題意知-1 因此,不等式a(x2+1)+b(x-1)+c>2ax的解集為(0,3). 評(píng)析這兩個(gè)不等式的求解,并不是多么困難,甚至可以說是簡單的,基于一般化思想未嘗不可,但如果關(guān)注到不等式的結(jié)構(gòu)特點(diǎn),則為快速而準(zhǔn)確解題,提供了必要條件,這也許就是模式化的極大好處. 分析一這是等式條件下利用均值不等式求最值的典型試題.問題(1)條件形式復(fù)雜,目標(biāo)結(jié)構(gòu)更簡單,從復(fù)雜到簡單容易操作,既可以利用消元法,又可以利用“1”的代換.問題(2)則是條件簡單,目標(biāo)復(fù)雜,從簡單到復(fù)雜構(gòu)造難.在解題技巧上可以利用“1”的代換,如果用消元法,則目標(biāo)式會(huì)越來越復(fù)雜,除了借助特殊不等式,似乎沒有更好的辦法.若能把問題(2)轉(zhuǎn)化為問題(1)的形式,則兩者的求解就統(tǒng)一了. 解(1)方法1:消元法. 方法2:“1”的代換. (2)方法1:“1”的代換. 方法2:消元后利用特殊不等式. 為了說明問題,我們先證明下面的不等式: 證明因?yàn)閍,b,x,y為正數(shù), 再看問題的解. 方法3:換元法. 評(píng)析特殊不等式的證明思路,正是源于問題(1)的求解方法2.問題(2)的方法1用技巧取勝,不太符合新高考命題理念,方法2以特殊不等式為背景,看似簡單,實(shí)際上增加了識(shí)記要求,如能抓住問題的本質(zhì),即“1”的代換,不用特殊不等式也是可行的.此時(shí)所謂“1”的代換,已經(jīng)不僅僅限于和為1,只要和為正常數(shù),都是可以的.對(duì)條件和目標(biāo)的結(jié)構(gòu)進(jìn)行變換,則問題(2)回歸到問題(1)的形式,難度自然降低. 分析二換個(gè)角度看問題(1).一般地,應(yīng)用均值不等式求最值,結(jié)構(gòu)上往往具有“給和求積”,“給積求和”的特點(diǎn).如果能將 “分式和結(jié)構(gòu)”的等式條件,變換成“整式積”的形式,那么,試題也就能回歸到更一般的解題模式上了. 評(píng)析相對(duì)于分析一的特殊解法,對(duì)于“給分式和求整式和”問題,將分式型等式條件化為整式等式條件,只需要進(jìn)行一次因式分解,湊一湊就行了,因式的構(gòu)成完全依賴于目標(biāo)的線性結(jié)構(gòu),無論系數(shù)與等式是否一致,都是可以的.這樣解題難度似乎又降低了不少. 不同知識(shí)點(diǎn)的試題,往往具有各自獨(dú)立而特別的解題模式,如數(shù)列問題的構(gòu)造模式,三角函數(shù)問題中的變角模式,解析幾何問題的運(yùn)算模式,等等.研究模式,洞悉模式,進(jìn)而利用模式,為快速解題創(chuàng)造得分條件,正是試題研究的方向之一,值得擁有.
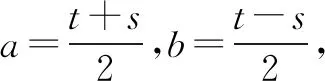
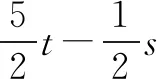
二、統(tǒng)一模式,提高解題速度





三、統(tǒng)一模式,降低解題難度