向量是表達幾何性質(zhì)的語言

沈海全

(浙江省紹興市越州中學 312000)

平面向量是高中數(shù)學中重要和基本的概念之一， 也是浙江高考的亮點和難點內(nèi)容. 它是溝通代數(shù)、幾何與三角函數(shù)的一種工具，有著極其豐富的實際背景,常用平面向量解決一些比較復雜的幾何問題，即幾何問題代數(shù)化.而在高考中某些向量問題常具有豐富的幾何背景和幾何性質(zhì)，反而需要把向量問題轉(zhuǎn)化為幾何問題，借助幾何方法來更好地解決，那就需要我們用敏銳的眼光識別向量語言中所蘊含的幾何性質(zhì)，這也是解決此類問題的難點.本文從課本習題出發(fā)通過一系列的拓展變式將一些具有明顯幾何意義的向量問題進行歸納總結(jié)，揭示問題的本質(zhì)，供老師同學參考學習.

一、在教材中尋根

人教版必修四課本P120 第2,3題.

1.已知向量a，b為非零向量，且|a+b|=|a-b|，求證：a⊥b，并解釋幾何意義.

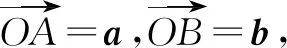
2.已知向量a，b為非零向量, 且(a+b)⊥(a-b)，求證：|a|=|b|，并解釋幾何意義.

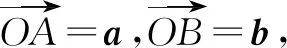
下面再看兩個小問題.

3.已知向量a，b滿足|a|=2，b·(a-b)=0，你能解釋其中蘊含的幾何意義嗎？

4.已知向量a，b滿足|a|=2，|b|=|a-b|，你能解釋其中蘊含的幾何意義嗎？

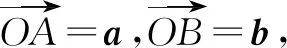
四個簡單的向量表達式，蘊含了我們最熟悉的平行四邊形、菱形、線段、圓所具有的最美的性質(zhì)．為變式拓展提供了材料和動力，結(jié)合以上性質(zhì)再加入新的元素|λa-b|設(shè)計了這么一個問題. 已知向量a，b滿足|a|=2，b·(a-b)=0，|b|=|a-b|，λ∈R，求|λa-b|的最小值.

解由以上幾個問題可知，b的終點B既在以線段OA為直徑的圓周上，又在線段OA的中垂線上，所以b唯一固定，而|λa-b|所表示的幾何意義為向量λa終點D和向量b終點B連線距離，即為直線OA上的動點D與定點B連線距離，所以表達的幾何意義為直線外一點與直線上一動點的最小距離，即|BD|min=|BC|=1.

二、在根基中求變

問題1已知向量a，b滿足|a|=2，a與a-b的夾角為60°，求|b|的最小值.

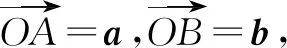
以上問題源于2010年浙江高考試題，體現(xiàn)了直線外一點到直線上動點連線的最短距離為垂線段長度.下面將條件a與a-b的夾角為60°改為b與a-b的夾角為120°,驚喜的發(fā)現(xiàn)b終點的軌跡由射線變?yōu)榱藞A弧，而初中已經(jīng)知道圓最優(yōu)美的幾何性質(zhì)是同弧所對的圓周角相等.這么優(yōu)美的幾何性質(zhì)以向量語言表現(xiàn)出來了.而解決這個問題又可以用正弦定理來解決，從而又用到了三角形最美的性質(zhì)即正弦定理.下面給出問題和解答.

問題2已知向量a，b，c滿足|a|=|b|=2，a⊥b，c=λa+(1-λ)b，λ∈R，求|c|的最小值.

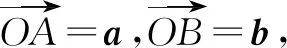
問題2是在問題1的基礎(chǔ)上再加進一個新的向量c，向量表達式c=λa+(1-λ)b體現(xiàn)了三點共線.變式1-4對各條件和角度進行了改變，產(chǎn)生了不同的幾何性質(zhì)，變式5更大膽地讓c也運動起來，最后轉(zhuǎn)化為兩圓相切問題.有了以上的探究，下面對2018年浙江高考平面向量試題進行分析,原來試題是那么自然而漂亮.

三、在真題中實踐

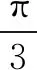
(b-e)·(b-2e)=0，即(b-e)⊥(b-2e).所以b的終點在以E1E2為直徑的圓周上.下面同解法一.

著名的藝術(shù)家羅丹說：“美到處都有，生活中不是缺少美，而是缺少發(fā)現(xiàn)美的眼睛.”本文中簡潔的向量表達式展現(xiàn)了平面幾何中一些最美的性質(zhì).這就需要教師在高考復習過程中精心選擇教學復習材料，精心設(shè)計教學過程.在教學過程中要注意知識發(fā)現(xiàn)的過程，讓學生體會知識的來龍去脈，使學生在發(fā)現(xiàn)知識的過程中，經(jīng)歷探究、思考、加工的過程，實現(xiàn)知識的“表象特征”到“內(nèi)在價值”理解升華.著力讓學生數(shù)學能力數(shù)學素養(yǎng)在數(shù)學問題的解決過程中生成、在教學互動的過程中成長、在思維思辨過程中升華.