淺談數形結合思想在小學低段教學中的應用
李巧瑞
【摘 要】小學生思維形式以具體形象思維為主,因此如何在解決問題中讓學生正確理解“數”與“形”的相對性,使之有機地結合起來,就能將復雜的問題簡單化。本文將重點介紹數形結合思想在小學低段教學中的應用。
【關鍵詞】數形結合思想;小學低段教學;思維習慣
中圖分類號:G612 文獻標識碼:A 文章編號:1006-7485(2020)21-0148-02
一、數形結合思想在教學中的重要作用
(一)數形結合思想有利于培養學生的“數感”和“符號”意識
如:在一年級認識1 - 10的數時,我們即要采用將實物和圖形與具體的數字對應起來。有幾個數我們就擺出幾個實物或者畫出幾張圖片。這樣學生能形象具體地感知到數字的大小和多少,在接下來的“加減法”教學中,如:“3+2=5”,我們將數字與實物對應,或者畫出具體的圖片呈現,學生一下子就明白了“3+2=5”的道理。這樣,在類似的教學中學生對數字有具體的感知,久而久之對數字變得敏感,進而再認識較大的數時,如“千”“萬”的認識通過擺方塊呈現“10個十是100,10個百是1000,10個千是10000”,也采用數形結合思想指引教學,學生就會在大腦中產生一種符號意識,這樣學生很容易接受新知識,使教學輕松推進。
(二)數形結合有利于培養學生良好的思維習慣
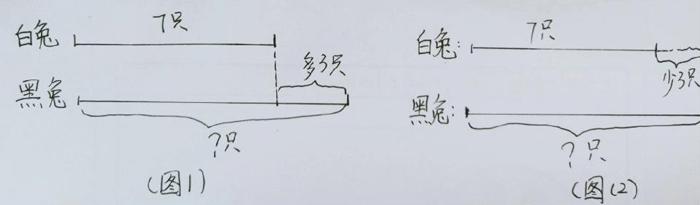
例如:教學“比多少”。草地上有白兔7只,黑兔比白兔多3只,黑兔有多少只?要求學生讀完題目找出條件和問題,并且要求其畫出線段圖來解決。(如圖1)
畫出線段圖,學生一目了然,列出算式7+3=10(只),而有些題目是這樣問的,白兔有7只,比黑兔少3只,那么黑兔有多少只?這時學生就容易出錯,很難理解題目中“比黑兔少3只”如果學生能用畫線段的思維方式入手,畫出圖(圖2)對照著圖形,學生就很容易理解到底是黑兔多還是白兔多,進而,很容易列出算式,7+3=10(只)。
(三)數形結合有利于打開解題思路,化難為易
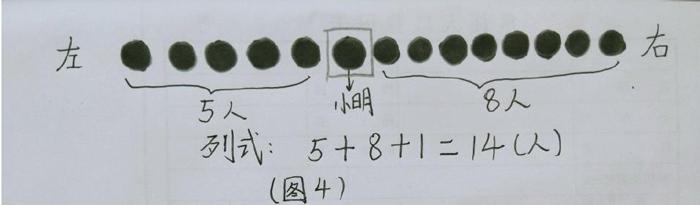
在小學低段中有些題目比較抽象,感覺無從下手,但如能有效運用數形結合的思想,打開解題思路,問題就會迎刃而解。如:課間小明和同學排成一行,他站在從左起的第6個位置,從右起的第9個位置,問這一行站了多少名同學?對于一年級學生,類似這樣的問題是比較困難的,如果我們借助小學生站隊已有的經驗,畫出做操時的隊形,就能變抽象為直觀,有效幫助學生解決問題。(圖4)
二、如何有效運用數形結合思想解決問題
(一)強化應用意識,提高應用能力
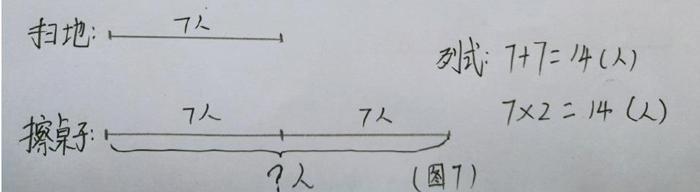
在教學中,教師應有這樣的導向,能畫圖的盡量將相對抽象的思考對象“圖形化”,逐步培養學生運用數形結合思想解決問題的能力,做到所謂的“潤物細無聲”。如:“倍數問題”。掃地的有7人,擦桌子的是掃地的2倍,求擦桌子的有多少人?(畫圖表示)學生們一眼就能看清楚,列式7x2=14(人)。為后面進行“差倍問題”做好鋪墊。(圖7)
教師加強在教學中數形結合思想的滲透,學生才能慢慢地形成應用數形結合思想解決問題的意識。
(二)深挖教材,養成運用數形結合思想解題的習慣
如:“鋪地磚問題”。學校有一段走廊長6米,寬3米,在走廊地面鋪上邊長是3分米的正方形地磚,需要鋪多少塊兒?通常我們給學生講用“大面積÷小面積=塊數”,60x30=1800(平方分米),3x3=9(平方分米),1800÷9=200(塊),但往往學生很難理解這種做法,那我們用數形結合思想怎么解決呢?30÷3=10(塊),60÷3=20(塊),10x20=200(塊),這種做法學生看起來一目了然,進而再去講解“大面積÷小面積=塊數”,這時學生就很容易理解其中的道理。還有解決問題中的典型行程問題,數形結合思想都是行之有效的數學教學思想。
(三)通過舉一反三練習將數形結合思想內化為解題方法
如:教學完“鋸木頭”問題后,可以舉一反三地給出以下練習題目。1.一根25cm長的鐵絲,把它剪成5cm長的小段,可以剪幾段?要剪幾次?2.一根鐵絲長15米,剪了4次,平均每段長多少米?3.一根繩子被剪了5次后,每段長4米,原來繩子有多長?4.時鐘4點鐘敲4下用12秒敲完,那么9點鐘敲9下,幾分鐘敲完?5.科學家上午6:00開始進行一次實驗,每隔3小時重復做一次,當他開始做第5次試驗時應是幾點鐘?
總之,在小學數學日常施教過程中,培養學生運用數學思想方法的意識和能力,鍛煉學生思維,可以切實提高學生的學習能力。我相信通過我們教師的深入鉆研,巧妙地將數形結合思想應用于課堂教學中,一定會引導學生由怕數學而愛上數學,在數學學科的學習上走得更遠。
注:本文為隴南市2018年度教育科學研究課題“數形結合思想在小學低年級數學教學‘解決問題領域的實踐研究”(課題立項號:LN[2018126)階段性研究成果。
參考文獻:
[1]符穎.感悟“數形結合”體會數學魅力——數形結合思想在小學數學課堂教學例談[J].小學教學研究,2018(14).
[2]賈威龍.淺談小學數學概念課的教學策略[J].吉林教育,2011(8).
(責編楊菲)

