基于音圈電機(jī)的魯棒控制器設(shè)計(jì)與仿真

胡永珊，李志濤，謝求泉，羅志良

(江西工業(yè)工程職業(yè)技術(shù)學(xué)院 機(jī)械工程學(xué)院，江西 萍鄉(xiāng) 337000)

0 引言

音圈電機(jī)(Voice Coil Motor,VCM)是一款由單相直流電直接驅(qū)動(dòng)的直線電機(jī)，可以實(shí)現(xiàn)高速高精度且力波動(dòng)較小的定位運(yùn)動(dòng)，由于沒有復(fù)雜的機(jī)械結(jié)構(gòu)，現(xiàn)在普遍運(yùn)用在三維運(yùn)動(dòng)平臺(tái)的Z軸，并搭配力-位置切換控制算法進(jìn)行推壓力控制。

魯棒控制主要用于那些被控對(duì)象存在高頻動(dòng)態(tài)不能建模以及系統(tǒng)存在一些不確定性參數(shù)等問題的運(yùn)控系統(tǒng)，其最核心的概念是得到被控對(duì)象的數(shù)學(xué)模型，分析系統(tǒng)具有的不確定因素和攝動(dòng)，通過對(duì)被控對(duì)象的伯德圖分析，選取相應(yīng)的加權(quán)函數(shù)，使系統(tǒng)能夠快速響應(yīng)動(dòng)態(tài)指令，并在一定的干擾下可以快速恢復(fù)自身的穩(wěn)定性，從而保證點(diǎn)到點(diǎn)運(yùn)動(dòng)的精準(zhǔn)定位。

在進(jìn)行魯棒控制器設(shè)計(jì)時(shí)，最重要的是在對(duì)應(yīng)的頻域段選取被控對(duì)象的不確定性上界函數(shù)和被控對(duì)象的性能加權(quán)函數(shù)，并要滿足系統(tǒng)抑制干擾能力強(qiáng)、動(dòng)態(tài)過程響應(yīng)快和穩(wěn)態(tài)過程整定精度高的性能要求；其次就是要盡量使所設(shè)計(jì)的魯棒控制器傳遞函數(shù)的階次低。為此，本文對(duì)基于音圈電機(jī)的魯棒控制器進(jìn)行設(shè)計(jì)與仿真。

1 建立音圈電機(jī)數(shù)學(xué)模型

在高速高精密的三維運(yùn)動(dòng)平臺(tái)中，音圈電機(jī)一般運(yùn)用在Z軸，由于音圈電機(jī)沒有自鎖結(jié)構(gòu)，每次下使能時(shí)，動(dòng)子會(huì)因自身重力而往下掉，并且不易確定其運(yùn)動(dòng)初始位置，所以在工程應(yīng)用時(shí)會(huì)用一個(gè)拉力彈簧或恒力氣缸來平衡動(dòng)子的重力，使音圈電機(jī)的動(dòng)子在去使能的狀態(tài)下可以處于一個(gè)固定的初始位置。所以在對(duì)音圈電機(jī)構(gòu)建數(shù)學(xué)模型時(shí)，可以將被控對(duì)象構(gòu)建成一個(gè)質(zhì)量-阻尼-彈簧系統(tǒng)(MFK系統(tǒng))，音圈電機(jī)力學(xué)模型如圖1所示。圖1中，F(xiàn)K為拉力彈簧的彈簧力，F(xiàn)G為電機(jī)動(dòng)子的重力，F(xiàn)C為系統(tǒng)的阻尼力，F(xiàn)為電機(jī)產(chǎn)生的推拉力,y為動(dòng)子的位移。

根據(jù)音圈電機(jī)工作原理，其等效電路模型如圖2所示。圖2中，U為音圈電機(jī)的母線電壓，E為音圈電機(jī)運(yùn)動(dòng)時(shí)產(chǎn)生的反電動(dòng)勢(shì)，L為動(dòng)子線圈等效電感，R為動(dòng)子線圈等效電阻，I為流經(jīng)動(dòng)子線圈的電流。

圖1 音圈電機(jī)力學(xué)模型 圖2 音圈電機(jī)等效電路模型

根據(jù)等效電路模型可以推導(dǎo)出音圈電機(jī)母線電壓平衡方程式：

(1)

其中：t為時(shí)間；B為定子產(chǎn)生的磁感應(yīng)強(qiáng)度；l為動(dòng)子線圈長(zhǎng)度；v為動(dòng)子的運(yùn)動(dòng)速度。

根據(jù)電機(jī)力學(xué)模型可以得到音圈電機(jī)力學(xué)平衡方程式：

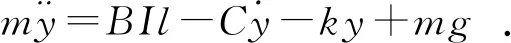
(2)

其中：m為動(dòng)子線圈的質(zhì)量；y為動(dòng)子的運(yùn)動(dòng)位移；C為電機(jī)的等效阻尼系數(shù)；k為彈簧的彈力系數(shù)；g為重力加速度。

將式(1)和式(2)進(jìn)行拉氏變換后再整理數(shù)據(jù)，就得到了音圈電機(jī)關(guān)于輸出運(yùn)動(dòng)位移y與相線輸入電壓u之間的數(shù)學(xué)模型，其傳遞函數(shù)P(s)表達(dá)式為：

(3)

2 系統(tǒng)辨識(shí)

在進(jìn)行魯棒控制時(shí)，先要對(duì)被控對(duì)象進(jìn)行系統(tǒng)辨識(shí)，得到被控對(duì)象的標(biāo)稱數(shù)學(xué)模型。一般在工程設(shè)計(jì)中均采用掃頻的方式來分析和獲取被控對(duì)象的模型參數(shù)，掃頻時(shí)常選用的激勵(lì)信號(hào)有正弦波、PBRS和Chirp等。

正弦掃頻是將整個(gè)運(yùn)控系統(tǒng)處于開環(huán)控制狀態(tài)，利用運(yùn)動(dòng)控制器產(chǎn)生一組模擬量電流信號(hào)來激勵(lì)音圈電機(jī)來回運(yùn)動(dòng)，并采集光柵尺的位置信號(hào)。該激勵(lì)信號(hào)是由一組在0 Hz～2 000 Hz的頻率段內(nèi)間隔一定步距的模擬量電流信號(hào)組成。

將運(yùn)控系統(tǒng)采集的模擬量電流信號(hào)和音圈電機(jī)光柵尺的位置信號(hào)進(jìn)行快速傅里葉變換，并在MATLAB里畫出伯德圖，如圖3所示。利用圖3可以在頻域里分析被控對(duì)象的幅值特性和相角特性。

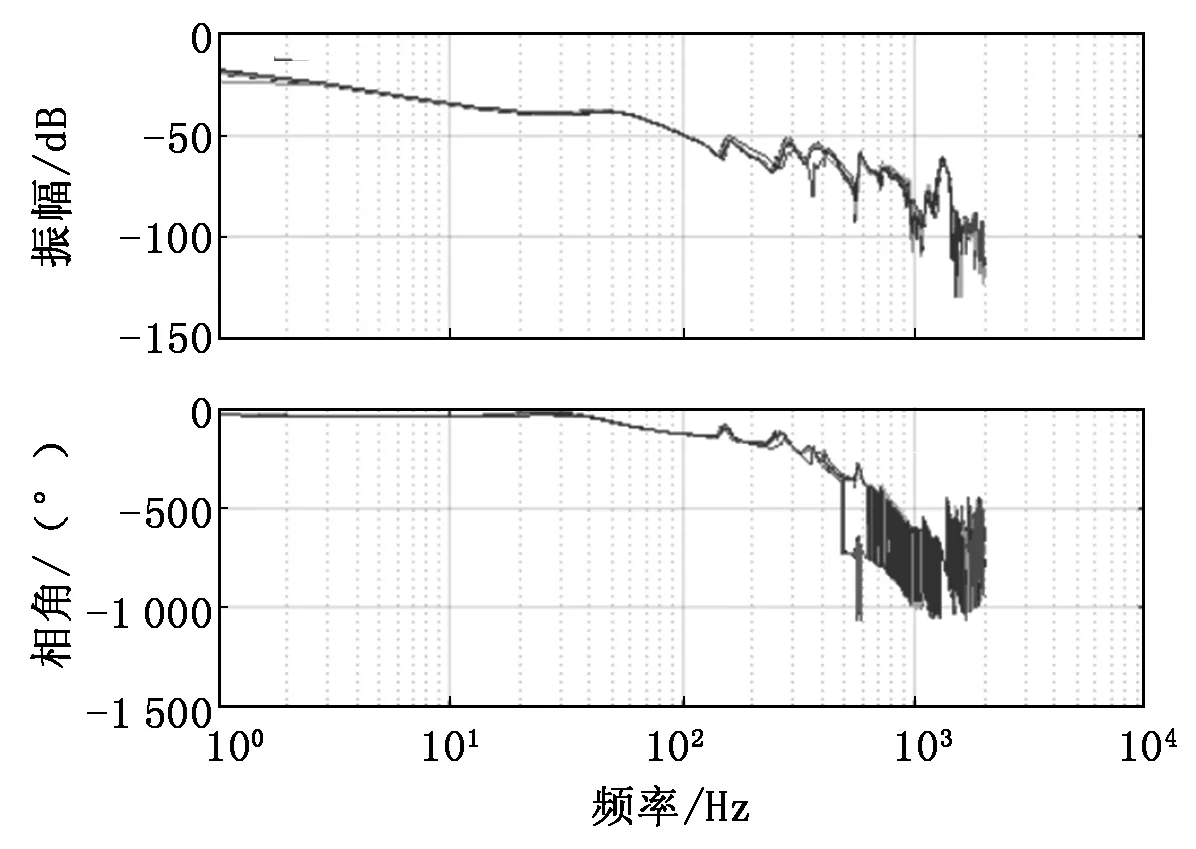
圖3 音圈電機(jī)經(jīng)正弦掃頻得到的伯德圖

將經(jīng)過快速傅里葉變換處理后所得到的頻率、幅值和相角等數(shù)據(jù)導(dǎo)入MATLAB軟件中，使用MATLAB系統(tǒng)辨識(shí)ident工具箱，通過分析被控系統(tǒng)的頻率特性曲線圖進(jìn)行最小二乘法擬合。

擬合方式選用零極點(diǎn)配置方式。通過選用不同組合的零點(diǎn)和極點(diǎn)，與被控對(duì)象的數(shù)據(jù)進(jìn)行最小二乘法擬合。分析經(jīng)多次擬合后的效果，選取其中匹配度最高的那組零點(diǎn)和極點(diǎn)。最后擬合結(jié)果匹配度最高的是3個(gè)極點(diǎn)和0個(gè)零點(diǎn)，這也正好可以驗(yàn)證機(jī)理數(shù)學(xué)建模的合理性。最終被控對(duì)象音圈電機(jī)所確定的數(shù)學(xué)模型的傳遞函數(shù)為：

(4)

對(duì)得到的傳遞函數(shù)進(jìn)行頻域分析以及動(dòng)態(tài)響應(yīng)性分析，并對(duì)掃頻所得的數(shù)據(jù)進(jìn)行不確定性及擾動(dòng)分析，為魯棒控制器設(shè)計(jì)做準(zhǔn)備。

3 魯棒控制器的設(shè)計(jì)

根據(jù)運(yùn)控系統(tǒng)要求的性能指標(biāo)和魯棒穩(wěn)定性，選擇用H∞混合靈敏度方法來設(shè)計(jì)控制器，其控制結(jié)構(gòu)如圖4所示。圖4中，W1、W2和W3為系統(tǒng)的加權(quán)函數(shù)，z1、z2、z3為系統(tǒng)的評(píng)價(jià)函數(shù)，Δ1、Δ2和Δ3為系統(tǒng)存在的不確定性擾動(dòng)，R1(s)為規(guī)劃位置輸入，e為位置跟蹤誤差，K(s)為H∞控制器，P(s)為被控對(duì)象標(biāo)稱傳遞函數(shù)，u為H∞控制器輸出，d為控制對(duì)象輸出的測(cè)量噪聲，w1、w2、w3為Δ1、Δ2和Δ3的輸出，Y(s)為實(shí)際位移輸出。

加權(quán)函數(shù)W1、W2和W3的標(biāo)準(zhǔn)框架如式(5)所示：

(5)

其中：G(s)為廣義被控對(duì)象；y為Y(s)控制器輸出。

圖4 被控對(duì)象基于混合靈敏度控制的控制器結(jié)構(gòu)

魯棒控制器性能的好壞依賴于權(quán)函數(shù)的選取。在選取加權(quán)函數(shù)時(shí)要注意各加權(quán)函數(shù)的特點(diǎn):W1主要用來抑制系統(tǒng)的高頻噪聲以及權(quán)衡高頻域中因不能建模的不確定性因素，所以該傳遞函數(shù)具有高通特性；W2用來抑制外界低頻干擾，確保系統(tǒng)在運(yùn)行中有較好的抗干擾能力和定位誤差跟隨調(diào)節(jié)能力，所以該傳遞函數(shù)具有低通特性；W3用來防止系統(tǒng)出現(xiàn)動(dòng)態(tài)跟隨誤差輸出過大和穩(wěn)態(tài)時(shí)積分過飽和而導(dǎo)致被控對(duì)象出現(xiàn)過沖或震蕩的現(xiàn)象。

最終選取的三個(gè)加權(quán)函數(shù)如下：

(6)

三個(gè)加權(quán)函數(shù)的伯德圖如圖5所示。

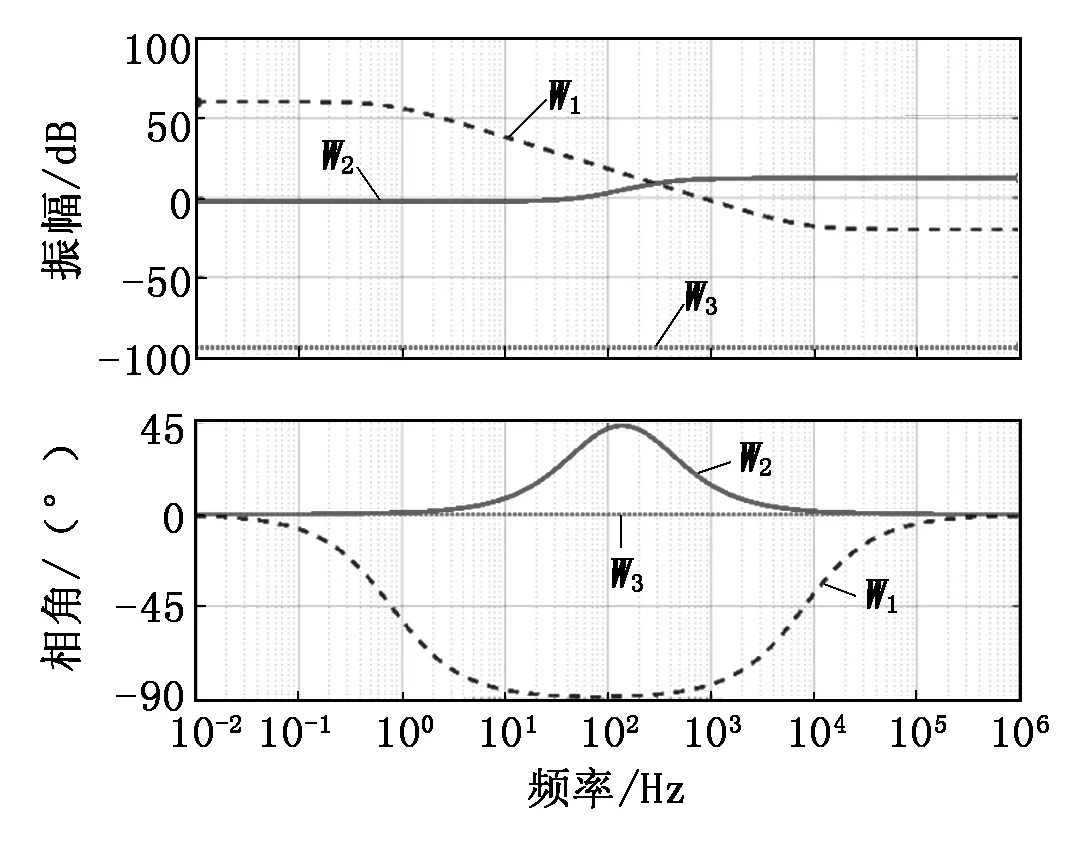
圖5 W1、W2和W3的伯德圖

最后根據(jù)三個(gè)加權(quán)函數(shù)，在MATLAB上求出魯棒控制器的傳遞函數(shù)，其傳遞函數(shù)的伯德圖如圖6所示。

4 仿真分析

4.1 分析方法

在MATLAB的Simulink模塊中搭建一套含魯棒控制算法、PID控制算法和開環(huán)控制算法的仿真系統(tǒng)，如圖7所示。

首先給系統(tǒng)觸發(fā)一個(gè)階躍單位信號(hào)，在示波器上得到相應(yīng)的階躍響應(yīng)曲線，分別來分析各個(gè)控制器的上升時(shí)間、超調(diào)量和調(diào)節(jié)時(shí)間，從而來分析控制器的動(dòng)態(tài)響應(yīng)性能和穩(wěn)態(tài)整定性能。

其次當(dāng)被控對(duì)象整定到穩(wěn)態(tài)時(shí)，再給系統(tǒng)觸發(fā)一個(gè)干擾信號(hào)，來分析魯棒控制器和PID控制器抑制干擾的性能。

4.2 仿真結(jié)果

首先在沒加干擾信號(hào)條件下，給系統(tǒng)觸發(fā)一個(gè)單位階躍激勵(lì)信號(hào)，得到如圖8所示的魯棒控制算法和PID控制算法的階躍響應(yīng)。

由圖8可知:在相同情況和條件下，魯棒控制器在動(dòng)態(tài)上升過程中沒有出現(xiàn)明顯的過沖，可以迅速地進(jìn)入穩(wěn)態(tài)過程；而PID控制器卻達(dá)不到這種效果，說明魯棒控制算法有良好的動(dòng)態(tài)響應(yīng)性能和穩(wěn)態(tài)整定性能。

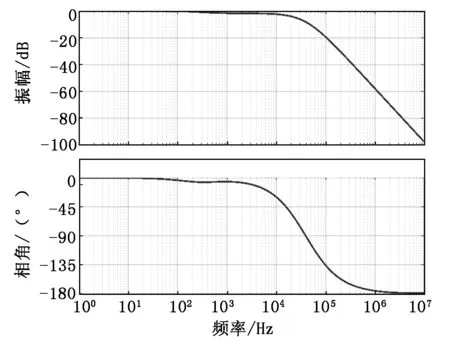
圖6 魯棒控制器的傳遞函數(shù)伯德圖

圖7 魯棒控制算法與PID控制算法性能對(duì)比仿真系統(tǒng)

然后再給系統(tǒng)觸發(fā)一個(gè)階躍激勵(lì)信號(hào)，待系統(tǒng)達(dá)到穩(wěn)定后，添加一個(gè)干擾信號(hào)，最后分別在示波器中得到魯棒控制器和PID控制器抑制干擾能力的結(jié)果，如圖9所示。

由圖9可知：當(dāng)遇到擾動(dòng)時(shí)，魯棒控制算法可以迅速恢復(fù)到穩(wěn)定狀態(tài)，且沒有出現(xiàn)顯著的波動(dòng)，從而驗(yàn)證了所設(shè)計(jì)的魯棒控制算法具有良好的抑制外來干擾的能力。

5 結(jié)論

通過與PID控制算法仿真對(duì)比，驗(yàn)證了魯棒控制算法較好地改善了被控對(duì)象的動(dòng)態(tài)響應(yīng)品質(zhì)和穩(wěn)態(tài)抑制干擾的能力。

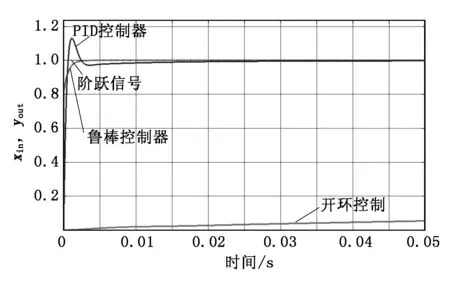
圖8 魯棒控制算法與PID控制算法階躍響應(yīng)對(duì)比

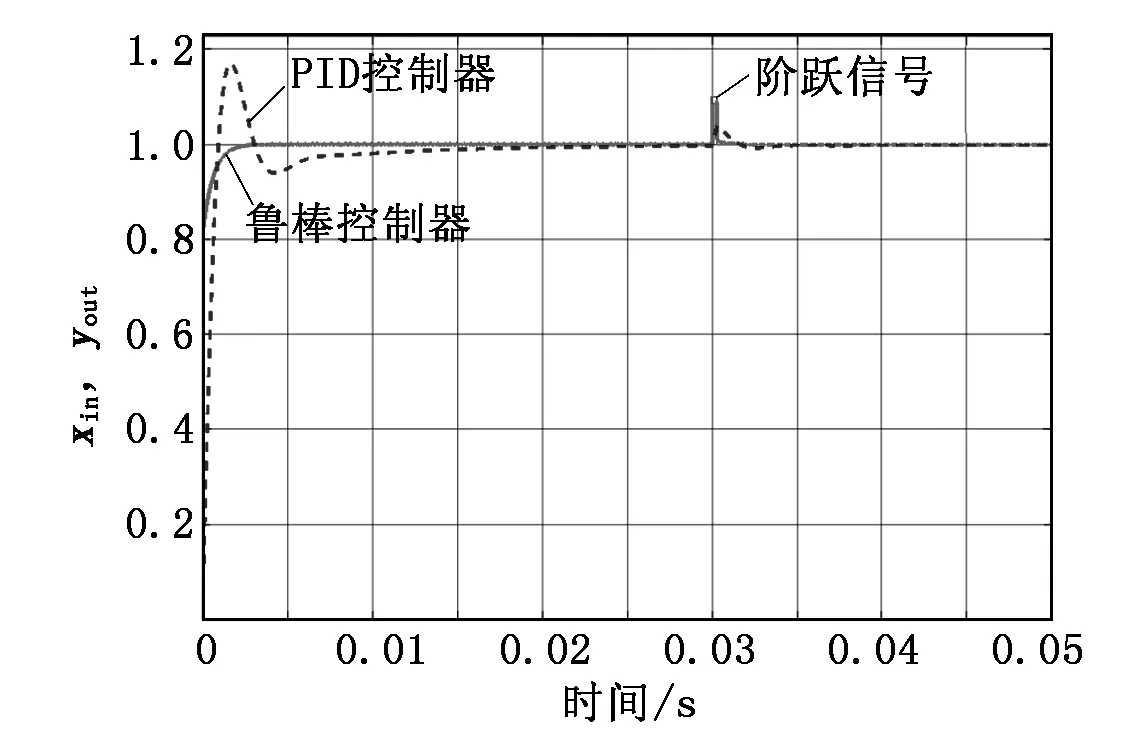
圖9 魯棒控制算法與PID控制算法抑制干擾性能對(duì)比