W36+離子雙電子復(fù)合的理論研究

丁軍順，符彥飆

(1.甘肅省武山縣第一高級中學(xué)，甘肅 天水 741300;2.西北師范大學(xué)物理與電子工程學(xué)院，甘肅 蘭州 730000)

1 概述

由于高熔點、低濺射和氚的滯留低等特點，鎢被用作國際熱核聚變實驗堆（ITER）主腔和偏濾器區(qū)的面壁材料[1-2]。也因此鎢離子會成為聚變的雜質(zhì)離子。在ITER等離子體中，電離平衡是電子的碰撞電離和各種復(fù)合過程的平衡，雙電子復(fù)合（DR）過程在其中起到很大的作用。因而，鎢離子DR過程的研究備受關(guān)注。Schippers等人[3]在海德堡重離子儲存環(huán)上對類氙W20+離子的DR過程進行了0～140eV范圍內(nèi)碰撞能量的實驗研究。實驗得出的等離子體DR速率系數(shù)與理論計算值存在較大差異。為解釋、解 決 這種差 異 ，Badnell等 人[4]利 用AUTOSTRUCTURE程序包對W20+離子的DR速率系數(shù)重新進行了計算。Spruck等人也對W18+([Kr]4d104f10)[5]和W19+([Kr]4d104f9)[6]在理論計算和實驗測量上進行了研究。Krantz等人[7]計算了W18+和W19+的DR速率系數(shù)。對于開4d殼層鎢離子，Ballance等人[8]計算了W35+基組態(tài)為4s24p64d3的4d→4f和 4p→4d的DR速率系數(shù)。Precal等人[9]利用AUTOSTRUCTURE計算了W37+到W28+(4dq,q=1-10)的部分DR速率系數(shù)。因為開4d和開4f殼層離子DR計算的復(fù)雜性，采用能級到能級的從頭計算的很少。對可能的輻射躍遷到可自電離態(tài)及其隨后的級聯(lián)退激（DAC）效應(yīng)的計算需要耗費很多資源和時間。但在Fu等[10]和Meng等[11]的研究發(fā)現(xiàn)DAC效應(yīng)對總DR速率系數(shù)的影響非常重要，應(yīng)該給予考慮。

本文利用基于全相對論組態(tài)相互作用方法的FAC程序包[12]計算了W36+([Zn]4p64d2)離子總的DR速率系數(shù)。計算包含了 [Zn]4p54d3nln’l’和[Zn]4p64d1nln’l’(n=4,5,6,n’＜24,l’＜12)所有內(nèi)殼層激發(fā)的能級。考察了不同激發(fā)與輻射通道對DR速率系數(shù)的貢獻(xiàn)，考慮了所有可能輻射躍遷到可自電離態(tài)及級聯(lián)退激（DAC）的影響，并進一步的利用外推的方法外推了n’=24-1000的結(jié)果。

2 理論方法

W36+離子俘獲一個特定能量的電子形成雙激發(fā)態(tài)，然后雙激發(fā)態(tài)輻射躍遷放出光子的DR過程可以簡單表示為：

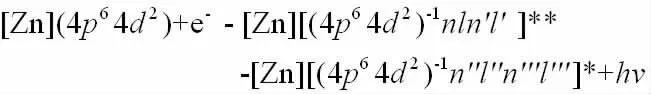
其中**表示中間雙激發(fā)態(tài)j,*表示輻射躍遷末態(tài)f.由初態(tài)i經(jīng)過雙激發(fā)態(tài)j再到所有輻射躍遷末態(tài)f的DR速率系數(shù)：

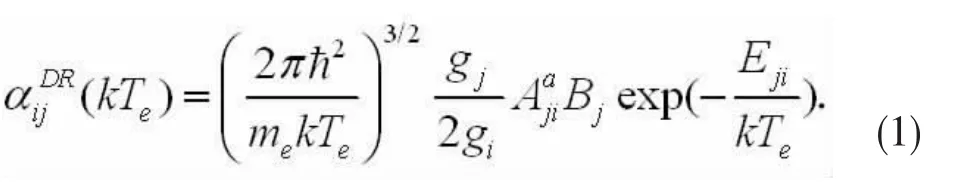
這里,Te是電子溫度,k是波爾茲曼常數(shù),Eij是共振能量,me是電子質(zhì)量,gi和gj分別是態(tài)i和態(tài)j的統(tǒng)計權(quán)重,Aaji是由態(tài)j到i的自電離速率；Bj是分支比, 其表達(dá)式為：

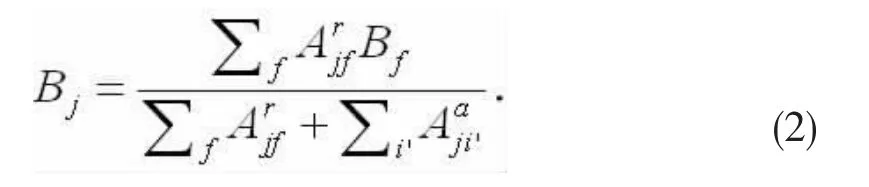
其中Aaji是態(tài)j到末態(tài)i′的俄歇速率,Arjf是態(tài)j到末態(tài)f的輻射躍遷速率,Bf是末態(tài)f的分支比，Aajf和Arjf分別由下式給出：

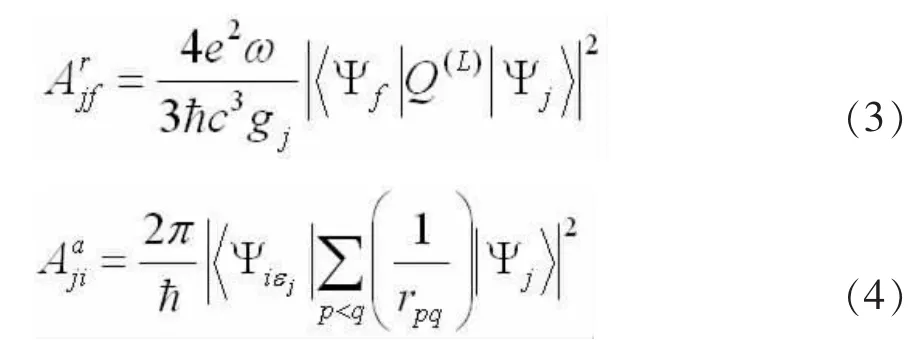
計算中,n′＜24的DR速率系數(shù)通過從頭計算得到,n′=24-1000的 DR速率系數(shù)通過 n′-3標(biāo)度率外推得到,外推公式為：

輻射復(fù)合(RR)和三體復(fù)合(TBR)過程作為另外兩種重要的電子－離子非彈性碰撞現(xiàn)象，其速率系數(shù)分別由如下的經(jīng)驗公式簡單估算得到[12]：

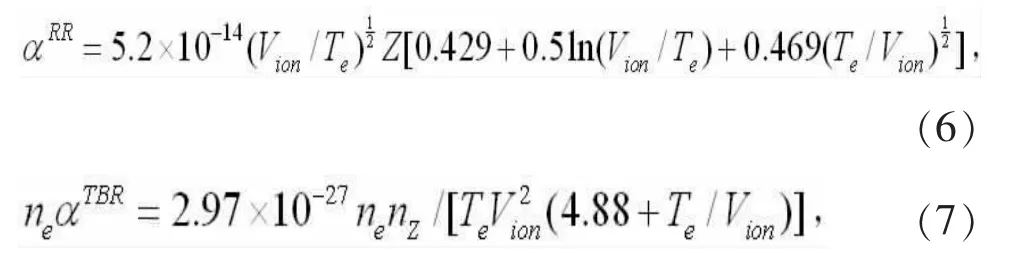
其中，Vion是電離勢，Z是電荷態(tài)，nZ是對應(yīng)離化態(tài)離子的最外層電子數(shù)，ne是電子密度，在本文的計算中取值1021cm-3。

3 結(jié)果與討論

3.1 W36+離子基態(tài)的磁偶極躍遷

為考察本文計算的準(zhǔn)確程度，表1給出了當(dāng)前計算的波長λ1FAC與其他已有數(shù)據(jù)的對比。其中，λ2exp是Radtke等人[13]實驗得到的數(shù)據(jù)，λ3MCDF是Pascal[14]使用MCDF計算得到的結(jié)果。可以看出，躍遷波長與實驗的（最大偏差為1.60%）和MCDF計算的（最大偏差為0.44%）都符合的很好。

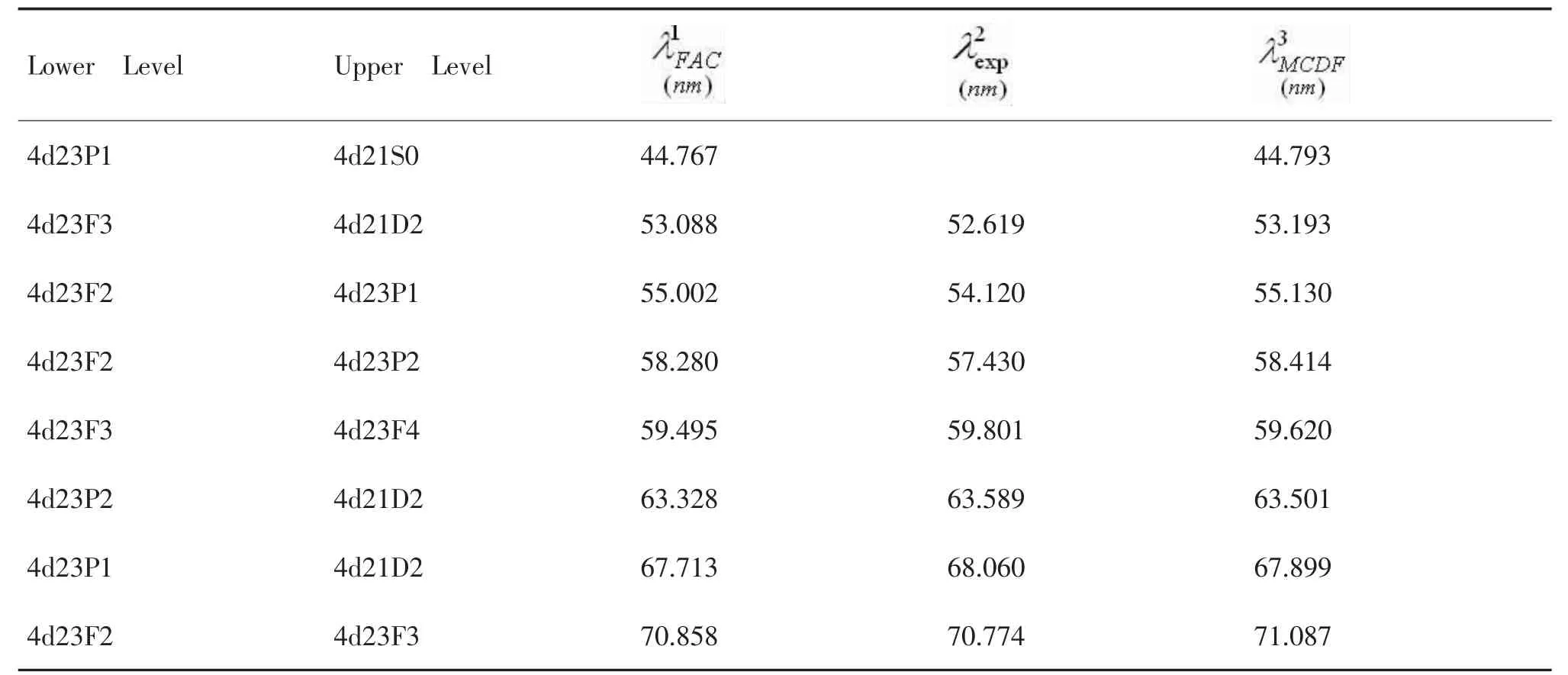
表1 當(dāng)前計算的W36+離子的波長與已有結(jié)果的對比

3.2 W36+離子不同通道的DR速率系數(shù)

由于多電子離子的結(jié)構(gòu)復(fù)雜且在計算中必須包含的內(nèi)殼層激發(fā)有非常多的能級，使計算DR過程需要大量的資源和時間，因此有必要選擇合適的DR通道，忽略一些貢獻(xiàn)小的通道。如圖1（a）所示展示W(wǎng)36+離子的中間雙激發(fā)態(tài)j=4(s,p,d)4l12f的DR速率系數(shù)，可以看出4d激發(fā)在低溫處占主導(dǎo)地位，4p激發(fā)在中高溫（>130eV）占主導(dǎo)地位。4s激發(fā)的DR速率系數(shù)在全溫度范圍都最小，其在峰值處4s激發(fā)占三者之和的5.06%，在正式的計算中可以忽略。

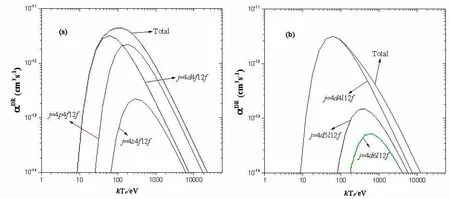
圖1 W36+離子中間雙激發(fā)態(tài)j=4(s,p,d)4l12f和j=4dnl12f(n=4,5,6)的DR速率系數(shù)

圖1（b）給出了 j=4dnl12f(n=4,5,6)的 DR 速率系數(shù)，其中j=4dnl12f的DR速率系數(shù)最大，j=4d5l12f的僅次于j=4dnl12f的，j=4d6l12f的DR速率系數(shù)最小。其中j=4d6l12f在峰值處占三者之和峰值的1.65%，且隨著n的增大，它的DR速率系數(shù)會急劇較小，因此本文計算中忽略n＞6的貢獻(xiàn)。

3.3 W36+離子的DAC效應(yīng)

如圖2所示，展示的是DAC、NDAC和RS+NRS的DR速率系數(shù)。RS+NRS表示同時考慮共振穩(wěn)態(tài)躍遷（RS）與非共振穩(wěn)態(tài)躍遷（NRS）。DAC是在考慮了RS+NRS效應(yīng)的基礎(chǔ)上進一步考慮可能輻射躍遷到可自電離態(tài)及隨后的級聯(lián)退激。NDAC是考慮了和DAC效應(yīng)相同的第一步躍遷，但不考慮隨后的級聯(lián)退激。由圖可見，隨著溫度的增大，三者的差異逐漸明顯，DAC效應(yīng)逐漸體現(xiàn)，在650eV處DAC效應(yīng)的貢獻(xiàn)為11.67%，并且DAC效應(yīng)的DR速率系數(shù)的計算值與RS+NRS效應(yīng)的計算值相差4.53%。在50000eV處，DAC效應(yīng)的貢獻(xiàn)是19.34%，和RS+NRS的計算值相差5.03%。因此在計算中必須考慮輻射躍遷末態(tài)分支比的影響，也就是考慮DAC效應(yīng)。

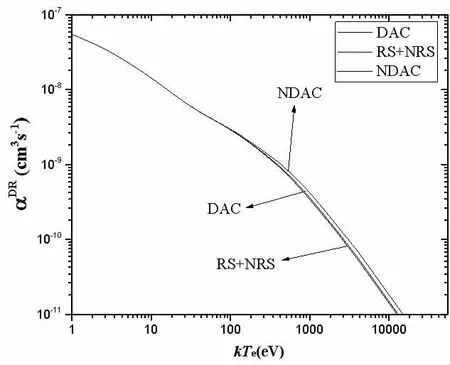
圖2 DAC、NDAC和NRS+RS的DR速率系數(shù)

3.4 W36+離子總的DR速率系數(shù)

圖3給出了以基態(tài)為初態(tài)的總DR速率系數(shù)，以及與ADAS數(shù)據(jù)庫、輻射復(fù)合（RR）和三體復(fù)合（TBR）速率系數(shù)的比較。圖中4d-total和4d-total分別表示4d和4p電子激發(fā)的總DR速率系數(shù)。4p電子激發(fā)的DR速率系數(shù)在全溫度范圍處于重要的主導(dǎo)地位，這與Fu等人計算的類鍶Sn12+離子的結(jié)果類似。外推部分的DR速率系數(shù)Sum(n'=24～1000)的貢獻(xiàn)和4d電子激發(fā)的DR速率系數(shù)接近。由圖可見，DR速率系數(shù)要比RR和TBR速率系數(shù)大的多，因此DR過程在電離平衡中會起主導(dǎo)作用。圖中OPEN-ADAS是ADPAK給出的結(jié)果，比較發(fā)現(xiàn)在高溫處本文計算的DR速率系數(shù)與ADAS數(shù)據(jù)庫提供的在曲線形狀上相似，但是在低溫處相差近兩個量級。在1000eV處ADAS的結(jié)果比本文計算的結(jié)果大54.45%，在10000eV處大71.69%。

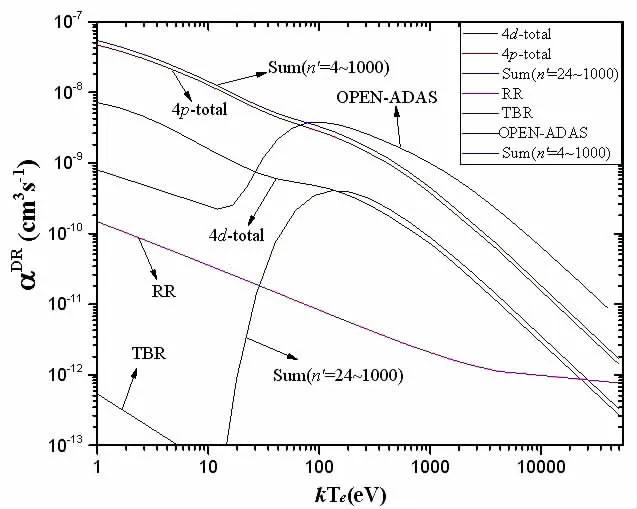
圖3 W36+離子基態(tài)的總DR速率系數(shù)

為了方便使用，我們對計算得到的基態(tài)能級的總DR速率系數(shù)利用公式（8）進行了擬合：

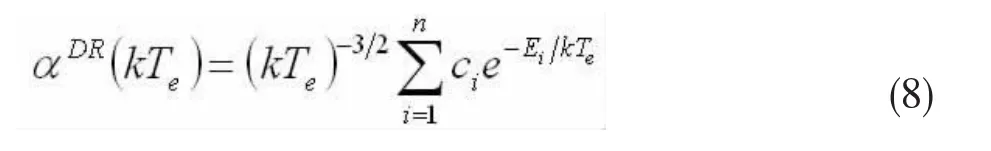
這里的ci和Ei是擬合參數(shù)，分別由表2和1給出。擬合出來的結(jié)果與我們的計算結(jié)果大部分偏差在1%以內(nèi)，有極少數(shù)偏差大于1%，最大偏差為3.31%。

表2 W36+離子DR速率系數(shù)參數(shù)擬合.M[N]代表M×10N

3.5 結(jié)論

本文基于全相對論組態(tài)相互作用的FAC程序包研究了類鍶W36+離子的DR過程，這是對復(fù)雜結(jié)構(gòu)基組態(tài)為 [Zn]4p64d2離子首次采用詳細(xì)的能級到能級的從頭計算。考察了不同通道對DR速率系數(shù)的影響， 詳細(xì)計算了 [Zn]4p54d3nln’l’ 和[Zn]4p64d1nln’l’(n=4,5,6,n’＜24,l’＜12) 所有內(nèi)殼層激發(fā)的所有能級的DR速率系數(shù)，然后通過對初態(tài)做了統(tǒng)計權(quán)重平均，對末態(tài)逐一求和得到總的DR速率系數(shù)。計算中特別關(guān)注了輻射躍遷到可自電離態(tài)及可能的級聯(lián)退激（DAC）的貢獻(xiàn)，并考慮了非共振穩(wěn)態(tài)和共振穩(wěn)態(tài)躍遷（NRS+RS）對DR速率系數(shù)的影響。結(jié)果發(fā)現(xiàn)隨著溫度的增大，DAC效應(yīng)的貢獻(xiàn)越來越重要，在650eV處DAC效應(yīng)的貢獻(xiàn)為11.67%，并且考慮DAC效應(yīng)的DR速率系數(shù)的計算值與考慮RS+NRS效應(yīng)的計算值相差4.53%。在50000eV處，DAC效應(yīng)的貢獻(xiàn)達(dá)到最大，是19.34%，和RS+NRS效應(yīng)的計算值相差5.03%。在總的DR速率系數(shù)中，4p殼層激發(fā)的DR速率系數(shù)起主導(dǎo)作用，在1～50000eV內(nèi)，4p激發(fā)的貢獻(xiàn)占總DR速率系數(shù)的85.54%～89.18%，但是4d激發(fā)的貢獻(xiàn)也不能忽略。此外，我們比較DR速率系數(shù)、RR速率系數(shù)和TBR速率系數(shù)時發(fā)現(xiàn)，DR速率系數(shù)比RR速率系數(shù)和TBR速率系數(shù)要大很多，這說明DR過程對電離平衡的影響更為重要。最后，為了方便使用我們對基組態(tài)的總的DR速率系數(shù)做了參數(shù)擬合，擬合的結(jié)果與我們計算的結(jié)果大部分偏差在1%以內(nèi)，有極少數(shù)偏差大于1%，最大偏差為3.31%。