基于影響矩陣法的鋼斜拉橋二次調索
嚴 松,王 耿
(中交第二公路勘察設計研究院有限公司,湖北 武漢430052)
1 概述
密索體系的整體式扁平鋼箱梁斜拉橋不僅具有傳統斜拉橋塔、梁、索合理協同受力的特點,還因自重輕、抗扭和橫向抗彎剛度大且便于工廠化生產等優點正成為現代城市橋梁發展中的翹楚,可滿足景觀需求。
鋼箱梁斜拉橋施工過程中大多伴有結構體系變化和結構荷載隨工序增加的特點。施工監控和及時糾偏是直接影響成橋狀態結構力學性能的與設計要求符合性的關鍵因素[1]。鑒于斜拉橋施工工序的復雜性以及各類施工綜合不利因素的影響,成橋階段主梁線形或索力狀態與設計理想狀態存在誤差,需進行二次調索以進行誤差調整。國內大多數斜拉橋施工中盡量保證線形并兼顧結構內力不超限,而在成橋后通過索力調整結構內力狀態[2]。
影響矩陣法已廣泛應用于斜拉橋和系桿拱橋的二次調索計算,其實用性已被許多工程實踐所驗證。斜拉橋成橋階段二次調索的索力調整量相較于被調前的索力小得多,且被調前的結構布置和內力狀態確定,運用線性假定結合單位荷載法并通過有限元模型計算可提取調整前結構的影響矩陣。選定不同的被調參數得到的影響矩陣的含義有所不同,調整參數與被調參數的相對大小也直接關系到方程組的求解方法。文章以國內某雙塔單索面鋼箱梁斜拉橋為工程背景,提出基于關心截面處索力調整的影響矩陣法,對成橋階段索力進行二次索力調整以滿足工程設計要求。
2 影響矩陣法
2.1 索力調整的矩陣表達式
二次調索前選取作為控制變量的某些關心截面上n個獨立結構特性參數所組集的列向量稱為調值向量{E},其中的單個元素可指定為內力調整量或位移調整量。結構中被調截面上指定調整以引起調值向量發生變化的m個獨立未知量所組集的列向量稱為被調向量{x},其中的單個元素為被調截面的內力或位移。影響矩陣[A]中(m×n陣)元素aij表示被調向量中的第j個元素發生單位變化引起調值向量中的第i個元素的變化量,見式(1)。二次調索的初始索力{T0}為成橋階段由頻率法原理實測的索力,二次調索后的目標索力{T}為設計索力。對于索力調整計算而言,我們關注的是截面位移以及索力變化量,將[A]矩陣關于關心截面處的位移元素依次置于末行,則{T}-{T0}對應于調值向量{E}中除位移行的索力調值向量部分。

在前述線性假定條件下,根據線性疊加原理,索力調整方程組的矩陣形式可寫為:

成橋階段索力計算調整時,被調向量個數m一般大于調值向量個數n,僅憑(2)式不能得到被調向量的唯一解。需提出索力優化的目標函數,采用優化算法求解對應目標函數的被調向量,即最優的索力調整向量。后文中將論述成橋階段以索力控制為主,標高控制為輔進行成橋階段誤差調整的方法,此時[A]矩陣中只包含關心截面處的索力元素,僅憑(2)式則可得到被調向量的唯一解。實際調索計算中通過有限元軟件結合Matlab可十分方便地進行索力調整計算。
2.2 影響矩陣的提取
二次調索階段結構存在初始索力,張拉任一根索對其余索的索力均有影響,主梁關心截面上的標高也會相應變化。如圖(1)b所示,i索兩端施以單位力P=1后,索內內力變化為 ΔF,圖(1)c中 i索端實際外力P=1-ΔF,故由圖(1)b所求得的控制點調值向量除以1-ΔF即可得到影響矩陣中第j列的向量。需要注意的是,根據擬定的合理調索順序對斜拉索逐根張拉得到的影響向量中包含了關心截面對應位置處位移變化量的元素,一般將其寫在向量的末端。則需控制位移變化量的關心截面數量即為m-n個。

圖1 影響向量計算示意圖
而對于成橋索力調整計算而言,特別對于塔梁墩固結體系的斜拉橋而言,若成橋后靠近主塔附近梁段的整體標高與設計有較大差距時,成橋階段對于索力的調整難以使成橋線形準確達到設計線形,而主要以成橋索力控制為主,避免因過度調整標高造成局部梁段應力超限或冗余度過小,影響運營期主梁安全。
2.3 施調向量{TS}的計算
成橋階段二次調索前、調索后的設計索力列向量為{T0}、{T},索力施調向量為{TS},不含位移元素的索力影響矩陣為[A],則索力調整計算式寫為:

實際施工監控中對成橋索力的調整計算需要建立準確的有限元模型,通過索力施調向量的不斷迭代計算,最終得到一組滿足索力誤差要求的成橋索力,而不可能與設計成橋索力完全一致。同時,根據局部調索過程中現場實測索力變化與理論計算值的差值,可實時調整模型中下一批索力施調量,在不斷的實測與理論計算對比調整過程中通過一次索力調整到達全橋索力調整的目標。施調向量{TS}的具體計算過程如下。
二期恒載下,計算模型中以擬定的最佳調索順序,根據影響矩陣法原理逐一施工階段對拉索施加固定力值的拉力,并逐一提取每階段全橋索力的變化量,對所有索力張拉施工階段的索力增量結果進行歸一化處理后即可得到索力影響矩陣[A]。
根據索力影響矩陣[A]和式(4),通過影響矩陣法和Matlab矩陣運算求出一次施調向量{TS1},得到的成橋索力向量{T1}與成橋設計索力向量{T}作差后再次代入式(4),計算出增調向量{FS1},則有:

從而模型中二次迭代計算的施調向量 {TS2}可寫為:

Midas模型計算時,用施調量{TS2}替代{TS1},即以原來調索順序將每個調索施工階段中的索力值換成{TS2}向量對應的索力值重新運行計算,得到的成橋索力向量{T2},可以發現{T2}更加接近于成橋設計索力向量{T}。同理,以索力向量的差{T2}-{T}再次代入式(4),計算出增調向量{TS2},依次類推迭代若干次后,{Tn}-{T}逐漸減小,當滿足設計要求的誤差限值時,則最后一次迭代計算得到的施調量{Tn}即可作為施調向量{TS}。
3 工程應用
某雙塔單索面鋼箱梁斜拉橋跨徑布置為50+96+192+70=408m,中心梁高3.0m,箱梁頂板寬29.5m,結構總體布置如圖2所示。

圖2 結構總體布置圖
3.1 全橋有限元模型的建立
采用MIDAS/CIVIL橋梁計算軟件建立有限元模型,梁單元模擬塔、梁和墩構件,只受拉桁架單元模擬全橋28對拉索,拉索、索塔與主梁節點之間均采用剛性連接。有限元模型如圖3所示。
圖3 有限元模型
3.2 提取索力影響矩陣[A]
成橋階段索力二次調整張拉過程中,遵循近塔端至遠塔端對稱張拉的原則,擬定設計張拉順序為 :B1.Z1/B14.Z14→B2.Z2/B13.Z13→B3.Z3/B12.Z12→B4.Z4/B11.Z11→B5.Z5/B10.Z10→B6.Z6→B7.Z7→B8.Z8→B9.Z9。在Midas施工階段中以此張拉順序單獨設置每對拉索施加單位力(10kN)為一個工況,逐工況疊加計算后再逆施工階段提取索力值作差后即可整理出索力相關影響矩陣。限于全部矩陣較大,現只列出16組的索力影響矩陣見表1。

表1 16組(共28組)索力影響矩陣
3.3 計算施調向量{TS}
由以上單位荷載法結合有限元軟件計算得到本例斜拉橋28階索力影響矩陣,結合Matlab矩陣運算得到二次調索最終索力施調向量{TS},即可由二次調索前全橋索力{T1}達到滿足成橋設計索力{T}的精度要求的最終成橋索力{T3},見表2,誤差不超過10%。
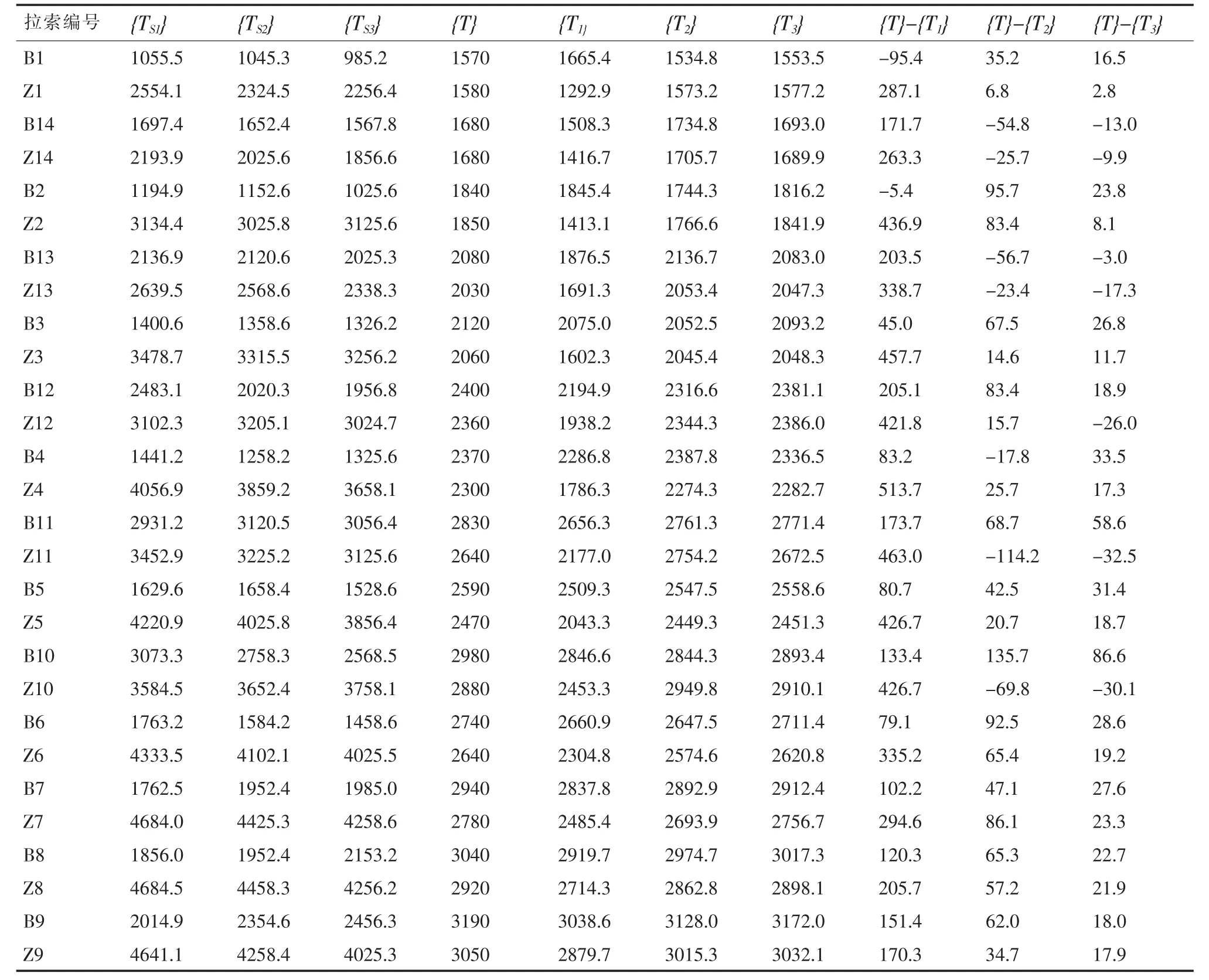
表2 二次調索索力施調向量以及成橋索力
3.4 二次調索結果
由表2調索結果可知:通過本文擬定的二次調索順序,結合索力影響矩陣法和有限元計算方法對成橋索力進行終調可在較少迭代次數條件下快速達到全橋索力的二次準確調整。索力調整前后對比如圖4所示。

圖4 索力優化前后對比
4 結論
文章斜拉橋索力監控的二次調索計算中,基于成橋索力誤差調整階段線性假定條件,采用單位荷載法求解索力優化的影響矩陣,并結合有限元模型計算得到遵循近塔端至遠塔端對稱張拉原則的索力施調向量,對全橋索力進行了準確的二次索力調整。
現場監控計算過程中通過有限次的有限元模型迭代計算便可快速達到設計索力的精度要求,成橋索力誤差限在10%以內,表明本文提出的索力二次調整計算的方案能滿足索力優化目標的基本要求,可作為施工監控的首選方案。

