保溫層對大體積混凝土溫度控制的影響分析
黃健


摘 要:針對大體積混凝土溫度場及溫度應力場,本文介紹了有限元計算理論,結合具體工程實例,建立其溫度控制的有限元分析模型,對標準工況下的混凝土溫度場和溫度應力場進行仿真模擬,分析不同保溫層參數對大體積混凝土溫度控制的影響,得出其變化規律,以期在大體積混凝土溫度控制中合理選擇保溫層。
關鍵詞:大體積混凝土;溫度控制;有限元;保溫層
中圖分類號:TU375.2文獻標識碼:A文章編號:1003-5168(2020)20-0128-03
Abstract: Aiming at the temperature field and temperature stress field of mass concrete, this paper introduced the finite element calculation theory, combined with specific engineering examples, established its temperature control finite element analysis model, and simulated the concrete temperature field and temperature stress field under standard working conditions, analyzed the influence of different insulation layer parameters on the temperature control of mass concrete, and derived its variation law, in order to select the insulation layer reasonably in the temperature control of mass concrete.
Keywords: mass concrete;temperature control;finite element;insulation layer
為保證大體積混凝土的澆筑質量,人們需要對其進行溫度控制,尤其是選擇合適的澆筑參數,對溫控防裂起到至關重要的作用[1-2]。大體積混凝土溫度場和應力場分布與保溫層參數呈非線性關系,無法利用解析法進行求解計算。本文通過有限元分析理論,進行大體積混凝土溫度場、溫度應力場仿真分析和計算,旨在分析保溫層參數對溫度控制的影響,指導大體積混凝土施工過程中的溫度控制。
1 混凝土溫控的有限元計算理論
大體積混凝土溫控的基本理論是熱傳導,具體來說,就是固體內有熱源的熱傳導,熱傳導的方程通常表示為[1]:
[?T?τ=λcρ(?2T?x2+?2T?y2+?2T?z2)+?θ?τ] ? ? ? ? ? ? ? ?(1)
式中,[c]為混凝土的比熱,kJ/(kg·℃);[ρ]為混凝土密度,kg/m3;[λ]為混凝土導熱系數,kJ/(m·d·℃);[τ]為時間,d;[θ]為混凝土絕熱溫升,[x]、[y]、[z]為內部位置坐標;[T]為內部坐標點對應的溫度值。
通過上述模型,人們可以對混凝土的溫度場進行求解;通過上述溫度場的分布,可以得出混凝土各點的溫度變形;通過混凝土的應力-應變關系,考慮其外在的約束條件,可以計算并得到其應力分布。
有限單元法對需要求解的區域進行劃分,通常劃分為數量有限多的單元個數,在每個劃分單元內,選擇特定的單元節點作為所求函數的插值節點,將求解方程中的變量重新進行改寫,轉化得到線性或非線性表達式,然后利用加權余量的方法,或者采用變分的原理,對上述方程進行離散和求解[3-4]。
2 工程實例
2.1 工程概況
河南省某水庫除險加固,需要新建溢洪道閘門,其中閘底板及閘墩采用混凝土澆筑,其均為大體積混凝土工程。綜合考慮施工條件等因素,閘底板采用跳倉法澆筑,每倉混凝土確定為長22 m、寬14.4 m,考慮環境溫度較低,采用混凝土表面覆蓋保溫材料的方法進行澆筑。
2.2 模型選取
關于有限元計算模型,在選擇地基范圍時,取混凝土澆筑尺寸的2倍,考慮混凝土體積較大,內部只設部分構造鋼筋,計算模型不考慮鋼筋的影響,采用素混凝土進行模型計算。混凝土初步確定澆筑溫度20 ℃、外界環境溫度14 ℃,每層澆筑厚度初步確定為2.4 m。
2.3 邊界條件確定
混凝土表面的養護選擇覆蓋保溫材料,可以選擇等效放熱系數法進行邊界分析,例如,參考文獻[1]方法,初步確定混凝土保溫面的等效放熱系數為396.8 kJ/(m2·d·℃)。其中,基巖與混凝土接觸面邊界條件采用第四類邊界條件,基巖與空氣接觸面邊界條件采用第三類邊界條件,其四周及下部可近似取為絕熱邊界條件。
3 有限元模型建立與求解
3.1 模型建立
選取適合模型的SOLID70等參數實體單元,當計算結構的溫度應力場時,可以進行必要的單元轉換,把溫度分析單元(SOLID70)和結構計算單元(SOLID45)單元進行耦合和轉化。考慮結構模型的對稱性,取結構的1/4建立模型,并采用映射剖分建立結構的有限元模型。
3.2 標準工況求解
對21 d混凝土及基巖的溫度變化進行有限元仿真模擬,得到21 d后其溫度場及溫度梯度分布,如圖1所示。混凝土內部溫度高于基巖溫度,由于基巖的保溫和空氣的擴散作用,最高溫度出現在基巖與混凝土的接觸面,最低溫度出現在混凝土與空氣的接觸表面。由于混凝土表面的溫度擴散最為明顯,該面的溫度梯度最大。對上述溫度場變化施加約束及荷載,得到其應力變化過程,如圖2所示。
溫度分布不均勻和時間效應累積會造成混凝土的溫度應力變化較大,而混凝土底板上部及四周與空氣進行熱交換,拉應力較大,而且出現在表面;考慮混凝土頂面邊角點受基巖的約束較弱,其出現最大拉應力區。經過仿真計算,混凝土最大拉應力出現在第7天,其拉應力值為0.77 MPa,小于相應容許拉應力1.73 MPa,其歷時曲線均在拉應力的容許值內,結構安全。
4 不同保溫層的仿真求解
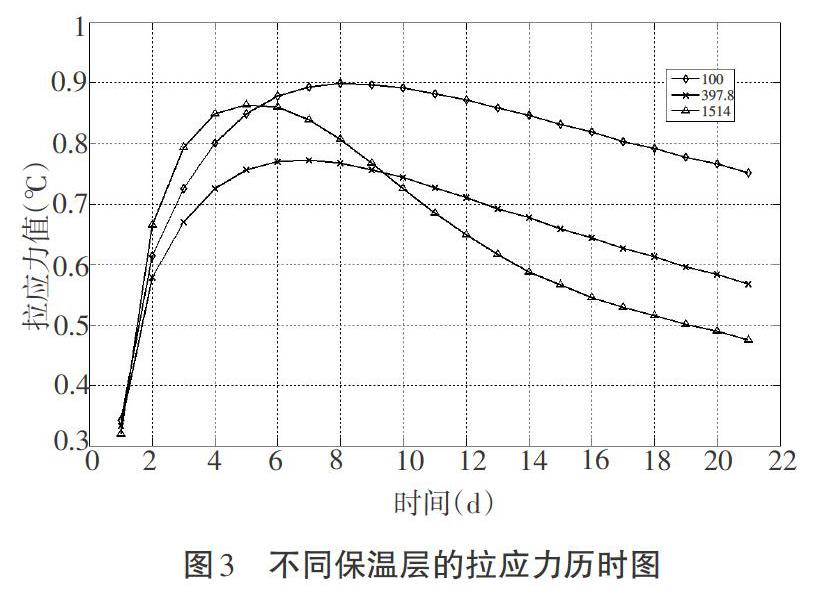
設置保溫層是混凝土溫控的重要手段,保溫層的設置會在一定程度上增加工程造價,在具體方案制定時,應注意合理選擇保溫層[5-6]。根據不同保溫層的保溫效果,選擇不覆蓋保溫層、覆蓋保溫層放熱系數分別為397.8和100的工況進行仿真計算,得出其最大拉應力的變化過程,如圖3所示;選取保溫層放熱系數100~1 514(不覆蓋保溫層)的各工況進行模擬,得出其最大拉應力的變化規律,如圖4所示。
由圖4可知,隨著混凝土表面保溫系數的減小,其最大拉應力值先減少后增加,而且出現明顯的后延。主要原因如下:保溫系數減少,延緩了其與外界空氣的散熱,可以減少最大拉應力,但保溫系數過小,會阻止水泥水化熱的向外釋放,進而導致熱量堆積,造成最大拉應力增加且滯后。結合本例而言,當保溫層放熱系數為600左右時,其最大拉應力最小,溫控效果最好,因此,在選擇保溫層時,應當充分考慮保溫層設置對溫控效果的影響,合理選擇保溫層的設置方法。
5 結語
混凝土保溫層的放熱系數減少,會導致最大拉應力先減少后增加,并出現時間明顯后延。在選擇保溫層設置方法時,人們不需要片面追求降低放熱系數,而應當在考慮工程造價的基礎上合理選擇保溫層,提高溫控效果。
參考文獻:
[1]朱伯芳.大體積混凝土溫度應力與溫度控制[M].北京:中國水利水電出版社,2012.
[2]王鐵夢.工程結構裂縫控制[M].北京:中國建筑工業出版社,2004.
[3]杜平,劉書賢,譚廣柱,等.基于四維溫度場理論的大體積混凝土數值分析[J].遼寧工程技術大學學報(自然科學版),2012(8):526-530.
[4]黃國權.有限元法基礎及ANSYS應用[M].北京:機械工業出版社,2004.
[5]胡紅軍,黃偉九,楊明波.ANSYS在材料工程中的應用[M].北京:機械工業出版社,2013.
[6]張朝暉.ANSYS12.0熱分析工程應用[M].北京:中國鐵道出版社,2010.

