雙弱面層狀巖體本構模型及其工程應用

姚錫偉，周 辀，陶盛宇

(1.內江職業技術學院，四川 內江 641000；2.成都理工大學 環境與土木工程學院，四川 成都 610059； 3.地質災害防治與地質環境保護國家重點實驗室，四川 成都 610059)

0 引言

在工程建設中,層狀巖體是經常遇到的巖體之一，其物理、力學性質受到內部節理面、層理面等軟弱結構面控制，是導致其具備各向異性的原因。在層狀巖體中，隧道開挖后圍巖的形變機制是較為復雜的，特別是其處于地質賦存條件與復雜地應力條件時，其破壞模式與破壞機制受軟弱面的影響更為顯著[1-2]，圍巖的穩定性控制面臨著較大的挑戰。

一些學者對層狀巖體的破壞特征、數值分析模型等展開了理論與試驗研究。Xu 等[3]采用室內三軸壓縮試驗，基于聲發射、電鏡掃描等測試手段對碳質千枚巖的力學特性進行了研究。王章瓊等[4]對鄂西北片巖單軸壓縮條件下的形變各向異性及水敏特性進行了分析。鄧華峰等[5]對單軸與三軸壓縮條件下層狀砂巖破壞模式的各向異性特征進行了分析。Cho等[6]采用單軸壓縮和巴西劈裂試驗，得到了片麻巖、頁巖和片巖的各向異性特性。吳章雷[7]通過現場原位試驗，描述了粉砂質板巖各向異性特征。夏彬偉[8]通過物理模擬試驗的方法得出了層狀巖體在隧道開挖后的變形特征。吳渤[9]建立了層狀巖體彈塑性各向異性力學模型，對層狀巖體隧道圍巖擾動區演化與錨固機理進行了研究。Xu[10]等通過耦合有限差分-離散元法，研究了層狀巖體在隧道開挖后細觀角度的力學損傷機理。黎立云等[11]通過斷裂力學與有限元方法，對層狀巖體斷裂破壞的現象與力學機制進行了分析。張春生等[12]基于離散元數值模型，對石英云母片巖各向異性特征的多尺度效應進行了精細化的分析。左雙英等[13]將層狀巖體的破壞模型分成5種，建立了基于彌散分析方法的巖石各向異性本構模型，并將其用于地下結構圍巖的破壞模式分析中。黃書嶺等[14]建立了考慮結構面特性的層狀巖體復合材料模型。王啟耀等[15]全面總結了傾斜層狀巖體的力學特征和數值模擬方法,并對各種模擬方法的優缺點進行了比較。王偉等[16]研究了軟硬相接巖層分布對隧道圍巖穩定性的影響，在卸荷巖體力學理論基礎上，考慮了6結構面傾角情況并進行了數值模擬分析。李林毅等[17]研究了單層襯砌結構力學特征，采用FLAC3D有限差分軟件，利用軟件內置的接觸面單元對不同結構層的層間接觸效應進行了模擬。

從上述分析可以看出，目前對于層狀巖體的研究，多只考慮1組軟弱結構面，即層理面的作用。而實際工程中，巖體的賦存條件較為復雜，往往存在著多組優勢結構面的共同作用。因此，建立多弱面作用下層狀巖體的力學本構模型具有重要的工程意義。本研究基于層理面彌散處理法(即力學模型中巖體僅受層面控制且具備各相異性的連續體)，建立層狀巖體雙弱面本構模型；采用該模型，對雙弱面層狀地層中圍巖的破壞模式進行系統分析。

1 雙弱面層狀巖體本構模型

1.1 簡化模型

圖1(a)中，層理面等作為最發育的結構面在實際的地質體中占據主導地位，此外也還有大量無序節理面發育。其中，優勢結構面由于具有明顯的方向性，其對巖體的力學特性影響較大；而無序分布的節理面由于其隨機性，可以將其作用等效于巖石基質體中，則巖體的力學模型就可以簡化為圖1(b)。

圖1 雙弱面層狀巖體力學模型Fig.1 Mechanical model of double-weak-plane layered rock mass

本研究需推導的模型應滿足以下強度和形變條件：

(1)在宏觀層面，層狀巖體的構成應僅為巖石基質體和層面(結構面)，軟弱結構面和巖石基質體均獨立考慮其強度特性，并且二者都必須符合帶拉伸截斷條件下的摩爾-庫倫強度準則。

(2)必須滿足橫觀各向同性理論。

1.2 彈性本構關系

模型中針對各組弱面都應設置以方位角和層面傾角為坐標軸的獨立坐標系。這些弱面可以任意正交或斜交，并根據實際巖體結構特征設置弱面的分布特性。

由橫觀各向同性理論可知，局部坐標系(x′,y′,z′，圖2) 下，層狀各向異性彈性矩陣為：

圖2 軟弱結構面坐標Fig.2 Coordinates of weak structural plane

(1)

應力轉換矩陣為：

R=

(2)

式中li，mi，ni(i=1, 2, 3)為下列矩陣的元素：

Q=

(3)

因此，可得到整體坐標系下應力應變關系為：

σ=RTSP′Rε。

(4)

式中，σ為應力矩陣；ε為應變矩陣。

可知，整體坐標系下的彈性矩陣為:

S=RTS′R，

(5)

式中S為6階矩陣，其分量記為Cij。

塑性應變增量通過塑性勢函數獲得，即：

(6)

式中λ，g和σ分別為基巖(或層面)的塑性指示因子、塑性勢函數和應力。

其總應變增量表達式：

Δε=Δεp+Δεe,

(7)

式中εe為彈性應變增量。

1.3 屈服準則

在力學性質方面，本研究模型將遵循帶拉伸截斷的Mohr-Coulomb準則進行巖石基質體與層理面的描述。其中，巖石基質體屈服準則為：

(8)

ft=σt-σ3，

(9)

式中，fs和ft分別為剪切和拉伸屈服法則的表達式；σ1和σ3分別為最大、最小主應力；Nφ=(1+sinφ)/(1-sinφ)；σt，φ，c分別為巖石基質體的抗拉破壞強度、內摩擦角、黏聚力。

相應的勢函數為：

gs=σ1-σ3Nψ,

(10)

gt=-σ3,

(11)

式中，gs為剪切勢函數；gt為拉伸勢函數，Nψ=(1+sinψ)/(1-sinψ)，ψ為巖石的剪脹角。

軟弱面的屈服準則為：

(12)

(13)

(14)

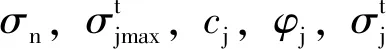
對應的塑性勢函數為：

(15)

(16)

1.4 塑性修正

FLAC3D中，本構模型二次開發最重要的步驟就是要對單元體進行塑性應力修正。根據其手冊中提出的推導建議，雙弱面模型塑性應力修正表達式如下。

當巖石的基質體發生剪切破壞時，

(17)

式中，σN和τN分別為修正后的法相應力和切向應力各分量值；σI和τI分別為修正前的法相應力和切向應力各分量值，且修正參數λs為：

(18)

當發生拉伸破壞時,

(19)

對于軟弱面而言，當發生剪切破壞時,

(20)

當發生拉伸破壞時,

(21)

圖3為通過C++語言對上述研究模型開展的二次開發流程。

圖3 模型開發流程圖Fig.3 Flowchart of model development

1.5 參數反演流程

由于模型參數眾多，準確快速地確定模型中各參數的取值是模型應用的關鍵。根據室內試驗結果，本研究采用的參數標定過程如下。

1.5.1形變參數標定

(1)選取層理面彈性模量對試樣彈性模量影響最小的加載角度標定巖石基質體的彈性模量。

(2)選取層理面彈性模量對試樣彈性模量影響最大的加載角度標定層理面的彈性模量。

1.5.2強度參數的標定

(1)選取層理面強度對試樣強度影響最小的加載角度標定巖石基質體的強度。

(2)根據各個角度下的抗壓強度值，對層理面的強度參數進行標定，將數值結果與試驗結果綜合比對，選取最為合理的強度值。

2 模型驗證

2.1 單弱面層狀巖體試驗驗證

目前層狀巖石力學特性的室內試驗研究均針對單一弱面結構。因此，本節進行模型驗證時，也只考慮1組層面的作用(用模型中的開關函數，忽略另1組層理面的作用) 。試驗數據來源于Konietzky 內單軸壓縮試驗結果[18]。建立的單軸壓縮數值模型如圖4所示。模型為圓柱體形狀，高10 cm，半徑2.5 cm，各層理之間相隔1 cm，模型底面設置軸向約束，側面和頂面不設置約束，并在模型上表面以1×10-7m/s的法向速度進行加載試驗。

圖4 數值計算的單軸壓縮試驗模型Fig.4 Uniaxial compression test model of numerical calculation

數值計算模型中各材料的力學參數詳見表1，數值計算結果如圖5所示，數值模擬與試驗試樣結果吻合較好。從圖5(a)可以看出，試樣角度層理面的傾角θ與強度值之間的關系呈U型分布，最小值在θ=60°時取得，最大值在θ=90°時取得。從圖5(b)可以看出，當θ=0°時，巖樣產生剪切破壞，此時層理面對巖樣的破壞模式影響較小；當θ=30°與60°時，巖樣產生沿層理面的剪切破壞；當θ=90°時，巖樣產生多個沿著層理面的劈裂破壞。

表1 參數Tab.1 Parameters

圖5 計算結果與室內試驗對比Fig.5 Comparison between calculated result and laboratory test

2.2 雙弱面層狀巖石單軸壓縮數值試驗

圖6 雙弱面層狀巖體示意圖Fig.6 Schematic diagram of rock mass with double-weak-plane

雙弱面層狀巖石間層理面夾角的幾何關系如圖6所示。其中，弱面2與豎向夾角為β，兩弱面之間的夾角為θ。本算例中，取θ=30°，β=0°～90°。每個弱面方向層理面間距為1 cm。

圖7為計算得到的巖石單軸抗壓強度與β的關系。可以看出，當β=0°時，弱面2平行于外力方向，弱面1與外力方向的夾角為30°，巖石的單軸抗壓強度最小；當β=30°時，弱面1與外力方向的夾角為60°，巖石的單軸抗壓強度略大于β=0°工況；當β=60°時，弱面1與外力方向垂直，巖石的單軸抗壓強度最大。可以發現，當兩個弱面中有1個弱面與外力方向的夾角為30°時，巖石的單軸抗壓強度最小。

圖7 單軸抗壓強度與β的關系Fig.7 Relationship between uniaxial compressive strength and β

2.3 單弱面層狀巖石隧道開挖穩定性

為了驗證模型的開挖效應，采用本研究的本構模型對單軟弱層面的層狀巖體在隧道開挖后的非對稱性破壞特性進行描述。建立圖8所示的計算模型，層理面傾角(層理面與隧道x軸正向夾角)為0°，45°，90°。模型為平面應變模型，隧道中心與其左右、上下邊界的距離均為40 m。除模型底部邊界外，將其余邊界均設置為法向應力邊界，而底部邊界約束豎向位移。采用在開挖邊界上施加與節點不平衡力相反方向的節點力來實現地應力的釋放。地應力場為均勻地應力場，即σx=σy=σz=15 MPa。圍巖的力學參數如表1所示。

圖8 計算模型Fig.8 Calculation model

計算結果如圖9所示。可以看出，當層理面傾角為0°或90°時，由于巖體結構對稱分布，圍巖的破壞區也對稱分布。對于0°而言，其拱頂與拱底區域的巖石由于層理面的彎折效應，塑性區分布范圍略大于拱腰；而對于90°而言，其拱腰區域的巖石由于層理面的彎折效應，塑性區略大于拱頂與拱底。當層理面傾角為45°時，圍巖的破壞區體現出強烈的非對稱分布特性。同時，左拱肩處巖體破壞最為嚴重，與實際工程觀察到的結果相似(圖9)。

圖9 圍巖破壞區Fig.9 Failure zones of surrounding rock

3 隧道開挖穩定性分析

3.1 數值模型

選取3種地應力場(均勻地應力場、豎向和水平構造應力場為主的應力場)研究層狀巖體雙弱面不同組合下隧道開挖后圍巖的破壞特征，其應力值分別為：σx=σy=σz=15 MPa，σx=σy=10 MPa，σz=15 MPa；σx=σy=15 MPa，σz=10 MPa。各種地應力場下計算工況如表2所示，圍巖及層理面的力學參數如表1所示，計算模型如圖8所示。其中，層理面傾角為層理面與隧道x軸正向夾角，層理面傾向為層理面與隧道軸線之間的夾角。

表2 計算工況Tab.2 Calculating conditions

3.2 雙弱面空間組合方式的影響

在應力場為σx=σy=σz=15 MPa的均勻地應力場條件下，雙軟弱層面在各類產狀的平行試驗結果(隧道開挖后圍巖破壞特征)如圖10～圖12所示。由于計算中弱面1的傾向與傾角不變，因此，對于每種組合，可以以弱面2的傾向與傾角簡稱，如組合90-60為弱面2傾向為90°、傾角為60°的工況。

圖10 工況1圍巖塑性破壞區分布Fig.10 Distribution of plastic failure zones of surrounding rock under working condition 1

從圖10可以看出，對于組合90-60而言，圍巖的塑性破壞區集中分布在隧道的右側，且右拱肩與右拱腳附近圍巖的破壞最為嚴重；對于組合90-90而言，圍巖的塑性破壞區主要分布在隧道的右拱肩附近，且左拱肩與右拱腳附近圍巖也在一定范圍內產生了損傷；對于組合90-120而言，圍巖的塑性破壞集中分布在隧道起拱線上側洞周附近的巖體處，且左拱肩破壞最為嚴重；對于組合90-150而言，隧道開挖后圍巖的破壞主要集中于隧道左側拱肩和拱腳附近(塑性破壞區)。

圖11 工況2圍巖塑性破壞區分布Fig.11 Distribution of plastic failure zones of surrounding rock under working condition 2

從圖11可以看出，對于組合30-60而言，圍巖的塑性破壞集中分布在隧道右側拱頂至拱腳附近，體現出極強的非對稱破壞特征；對于組合30-90而言，圍巖的塑性破壞集中分布在隧道左拱肩與右拱腰附近；對于組合30-120而言，圍巖的塑性破壞集中分布在隧道拱底至右拱肩范圍內，且隧道拱底的塑性破壞最為嚴重；對于組合30-150而言，圍巖的塑性破壞區較為對稱地分布在隧道左右拱腰兩側，且右側圍巖的破壞區范圍略大于左側。

圖12 工況3 圍巖塑性破壞區分布Fig.12 Distribution of plastic failure zones of surrounding rock under working condition 3

從圖12可以看出，對于組合0-60而言，圍巖的塑性破壞主要集中在右拱腳附近；對于組合0-90而言，圍巖的塑性破壞區域在隧道左右兩側分布較為均勻，且主要集中在左右拱腰附近；對于0-120而言，圍巖的塑性破壞集中分布在隧道拱頂至左拱腰附近，體現出極強的非對稱性；對于0-150而言，圍巖的塑性破壞區域主要集中在右拱腳附近，破壞形態與組合0-60相似。

對比圖10～圖12可以看出，雙軟弱面圍巖中弱面間的傾向與傾角的組合對圍巖破壞模式有很大影響，多數情況下均體現出明顯的非對稱破壞特征。

3.3 地應力場的影響

以工況1為例，分析地應力場對圍巖破壞模式的影響。圖13、圖14分別為側壓力系數λ=σy/σx>1與λ<1時時圍巖的塑性區分布。與圖10對比可以看出，對于不同構造應力場條件下的相同組合而言，隨著弱面2傾角的增加，圍巖破壞模式之間的差異逐漸增大。當組合為90-60時，不同地應力場條件下的圍巖破壞區域相似，只是破壞程度有所差異；而當組合為90-150時，圍巖破壞形態之間的差異很大，λ<1時圍巖破壞區域集中分布在左拱腳附近；λ>1時在隧道拱腰兩側對稱分布；λ=1時集中分布在左拱肩與左拱腰附近。

圖13 工況1圍巖塑性破壞區分布(λ>1)Fig.13 Distribution of plastic failure zones of surrounding rock under working condition 1(λ>1)

圖14 工況1圍巖塑性破壞區分布(λ<1)Fig.14 Distribution of plastic failure zones of surrounding rock under working condition 1(λ<1)

可以看出，對于雙弱面層狀巖體而言，圍巖的破壞模式受到弱面的空間形態與地應力場的共同控制，大多數情況下均體現出明顯的非對稱破壞特征。因此在實際工程中，要根據巖體弱面的實際組合，找出圍巖的關鍵破壞位置，然后進行針對性的加強支護來控制圍巖的非對稱變形。

4 結論

本研究基于層理面的彌散處理方法，建立了層狀巖體雙弱面本構模型。采用該模型，對雙弱面層狀地層中圍巖的破壞模式進行了系統分析，得到以下結論：

(1)巖石強度、形變與破壞形式的各項異性特征可以通過開發的雙弱面模型很好地表現。

(2)雙軟弱面圍巖中弱面間的傾向與傾角的組合對圍巖的破壞模式有很大的影響，大多數情況下均體現出明顯的非對稱破壞特征。

(3)對于不同構造應力場條件下的相同組合而言，隨著弱面傾角的增加，圍巖破壞模式之間的差異逐漸增大。

隧道的開挖是一個卸荷過程，因此，下一步應該從室內試驗與數值模擬兩個方面對雙弱面層狀巖石的卸荷力學特性進行研究；同時，基于雙弱面層狀巖體中隧道開挖的圍巖破壞形態，可以進行針對性的非對稱形變控制措施研究。