基于多標(biāo)簽層次聚類的GPR圖像雙曲波提取方法

李文生，原 達(dá)，苗 翠，王冬雨

基于多標(biāo)簽層次聚類的GPR圖像雙曲波提取方法

李文生，原 達(dá)，苗 翠，王冬雨

(山東工商學(xué)院智能信息處理重點實驗室，山東 煙臺 264005)

探地雷達(dá)(GPR)圖像雙曲波提取是分析地下目標(biāo)位置和結(jié)構(gòu)的重要方法，但在真實環(huán)境中，由于噪聲和雜波的干擾，使得提取出的雙曲波存在結(jié)構(gòu)不完整、碎片化和形狀異常等問題，不利于數(shù)據(jù)分析和三維建模等后續(xù)操作。為此，提出了一種基于多標(biāo)簽層次聚類的雙曲波提取方法(MHCE)。首先通過信息熵評價像素鄰域的穩(wěn)定性，構(gòu)造了基于信息熵的距離度量來進(jìn)行層次聚類；然后利用聚類后的鄰接空間進(jìn)行多標(biāo)簽聚類以降低雜波和噪聲對雙曲波提取的影響；最后結(jié)合多標(biāo)簽聚類結(jié)果的擬合形狀和紋理方向提取雙曲波。實驗表明，該方法對于真實GPR圖像雙曲波具有較好的魯棒性，能夠獲得規(guī)范化的雙曲波形狀和位置參數(shù)。

探地雷達(dá)圖像；雙曲波；信息熵；多標(biāo)簽層次聚類；魯棒性

探地雷達(dá)(ground penetrating radar，GPR)作為一種探測介質(zhì)內(nèi)部特性和分布規(guī)律的無損探測方法，已被廣泛應(yīng)用于建筑、采礦、環(huán)保、考古、市政工程、軍事等領(lǐng)域[1-3]。對GPR圖像雙曲波的提取有助于精確推斷地下埋藏物內(nèi)部結(jié)構(gòu)和目標(biāo)的深度、形狀等重要信息。在真實環(huán)境中，GPR所接收到的信號十分復(fù)雜，雙曲波提取受到了諸多因素的影響。首先，電臺、無線電廣播等信號源發(fā)射的無線信號可以使GPR圖像中形成許多排列緊密的小型雜波，雜波過多會模糊其他雙曲波的波形。尤其是在天線附近，磁場影響嚴(yán)重，極易導(dǎo)致GPR圖像中的數(shù)據(jù)發(fā)生錯位或部分丟失。同時，脈沖余振、系統(tǒng)內(nèi)部干擾、地表不光滑或地下介質(zhì)不均勻等引起的散射以及剖面旁側(cè)的繞射等都會在圖像中形成雜波[4]，影響圖像質(zhì)量。其次，在采集過程中，雙曲波的形狀和清晰度容易受到采集速度和深度的影響。采集速度過快會導(dǎo)致雙曲波波形過寬。并且隨著探測深度的增加，信號振幅相應(yīng)地減小[5]，導(dǎo)致雙曲波的清晰度逐漸降低。最后，不同結(jié)構(gòu)的地下介質(zhì)會使圖像產(chǎn)生不同類型的噪聲，如雪花噪聲、高斯噪聲等[6]。這些問題為建立完整的GPR圖像樣本集和在真實環(huán)境中進(jìn)行雙曲波提取帶來了挑戰(zhàn)。

許多基于有監(jiān)督學(xué)習(xí)的雙曲波提取方法憑借準(zhǔn)確和魯棒的特點受到了廣泛的關(guān)注。TORRIONE等[7]使用支持向量機(jī)(support vector machine，SVM)和HOG特征進(jìn)行GPR圖像雙曲波識別并取得了較好的效果。TBARKI等[8]提出使用OSVM (one-class SVM)進(jìn)行GPR圖像地雷檢測，表明OSVM在數(shù)據(jù)類別不平衡時由較大優(yōu)勢。GIOVANNESCHI等[9]使用字典學(xué)習(xí)方法獲取了GPR數(shù)據(jù)的稀疏表示，并利用SVM進(jìn)行雙曲波識別，提高了雙曲波提取的準(zhǔn)確度。MISSAOUI等[10]考慮到不同干擾源對應(yīng)的雜波類型不同，提出MDHMM算法通過融合不同類型的雜波實現(xiàn)高檢測和低誤報率。ZHANG等[11]利用Gibbs sampling獲取模型參數(shù)，在初始化參數(shù)方面具有更強(qiáng)的魯棒性。MANANDHAR等[12]將隱馬爾可夫模型(hidden Markov model，HMM)與多示例學(xué)習(xí)框架(multiple-Instance learning，MIL)結(jié)合進(jìn)行雙曲波識別，并使用貝葉斯方法推測HMM參數(shù)以提高識別性能。盡管HMM在雙曲波識別中可以取得較好的識別效果，但其參數(shù)初始值對識別效果影響較大。此外，MAAS和SCHMALZL[13]也將神經(jīng)網(wǎng)絡(luò)(neural network，NN)[14]用于雙曲波識別。有監(jiān)督學(xué)習(xí)使用訓(xùn)練模型識別雙曲波，具有較強(qiáng)的魯棒性及泛化能力，然而這類方法對特征提取質(zhì)量要求較高，特征提取的效果會直接影響模型的識別性能。

MAAS和SCHMALZL[13,1]使用Hough變換擬合目標(biāo)參數(shù)以提取雙曲波。Hough變換通過在參數(shù)空間中投票來確定目標(biāo)參數(shù)，該方法擁有較高的擬合精度，但時間復(fù)雜度高。DOU等[15]根據(jù)列間的連接情況對像素聚類，將其結(jié)果從波谷分裂為多個簇，并根據(jù)各簇的形狀特征進(jìn)行雙曲波提取。該算法具有較高的準(zhǔn)確率，但只考慮了形狀特征，雙曲波提取時容易受到噪聲的干擾。在此基礎(chǔ)上，KAFEDZISKI等[16]結(jié)合Hough和DOU等[15]提出的聚類算法在純凈的GPR數(shù)據(jù)中取得了較高的準(zhǔn)確率，但該算法在真實GPR中受噪聲和雜波的影響較大。ZHOU等[17]考慮了雙曲波間存在相交部分的情況，提出了OSCA算法進(jìn)行雙曲波提取，該方法在只具有少量雜波和噪聲的GPR圖像中取得了較高的準(zhǔn)確度，但存在噪聲干擾時很難提取完整的雙曲波。

1 MHCE算法描述

基于多標(biāo)簽層次聚類的雙曲波提取算法(multi- label hierarchical clustering-based hyperbola extraction method，MHCE)的實現(xiàn)分為預(yù)處理、多標(biāo)簽層次聚類、雙曲波提取3個階段，如圖1所示，第1階段結(jié)合引導(dǎo)圖濾波[18]和最大類間方差法(Otsu)[19]獲取了圖像的二值圖；第2階段為層次聚類算法構(gòu)造了基于信息熵的距離度量，并基于聚類結(jié)果的鄰接空間提取與雙曲波具有相同鄰接結(jié)構(gòu)的像素子集；第3階段結(jié)合像素子集的擬合形狀和紋理方向進(jìn)行雙曲波提取。MHCE的核心是多標(biāo)簽層次聚類算法，該算法能夠去除不符合雙曲波數(shù)據(jù)分布特性的像素子集，減小雙曲波提取階段的計算量，并提高雙曲波提取的準(zhǔn)確率。

1.1 多標(biāo)簽層次聚類

本文為層次聚類算法構(gòu)造了基于信息熵的距離度量，并利用聚類結(jié)果的鄰接空間進(jìn)行多標(biāo)簽聚類。多標(biāo)簽聚類之后，任何與雙曲波的鄰接結(jié)構(gòu)相同的像素子集將被賦予一個標(biāo)簽，部分像素?fù)碛械臉?biāo)簽數(shù)量不止一個。

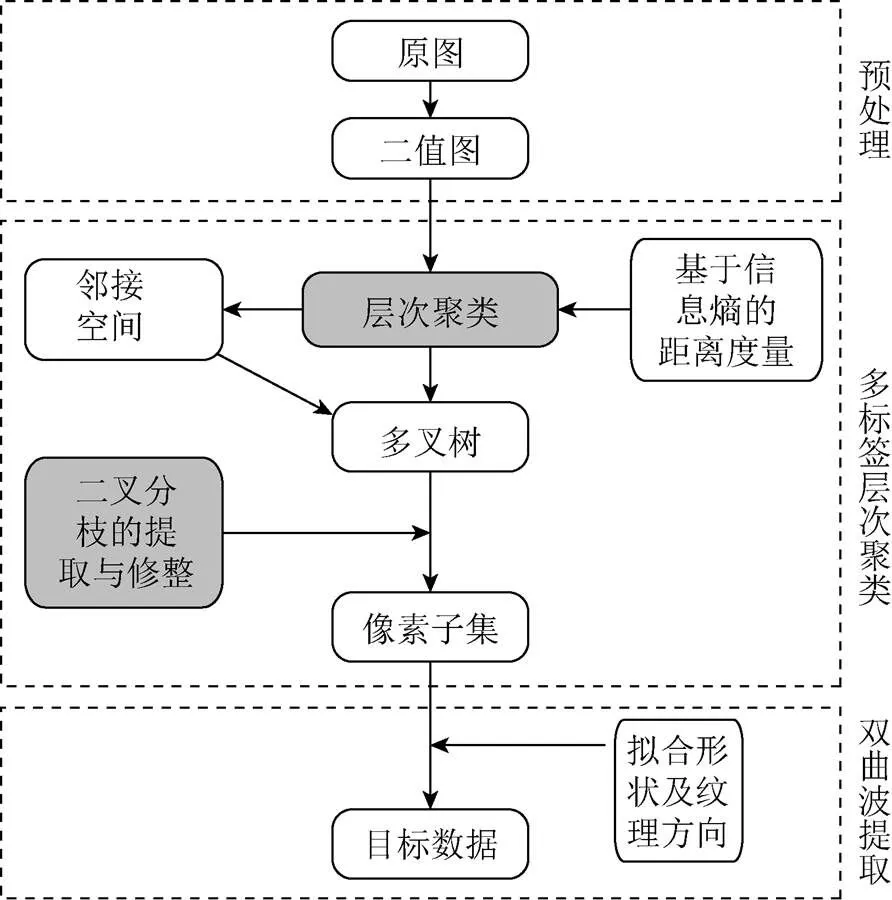
圖1 算法流程圖

1.1.1 基于信息熵的距離度量

本文使用信息熵評價像素鄰域的穩(wěn)定性，并將其作為層次聚類算法的距離度量。本節(jié)首先定義了分支和行段的概念，然后介紹了如何使用信息熵評價像素鄰接空間的穩(wěn)定性，并在最后給出了基于信息熵的層次聚類算法的實現(xiàn)流程。

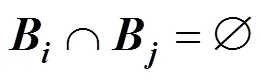
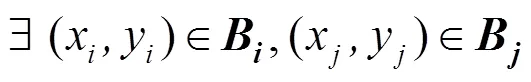
對于任意2個擁有不同形狀的像素集合，其分支間相同的鄰接方向?qū)?yīng)鄰接空間的結(jié)構(gòu)可能不同，如圖2所示，當(dāng)分支在水平方向存在鄰接關(guān)系時，雙曲波和非雙曲波分支的鄰接空間是相同的，然而當(dāng)分支在豎直方向存在鄰接關(guān)系時，雙曲波分支的鄰接空間呈等腰三角形，但非雙曲波的鄰接空間呈直線型。顯然使分支在豎直方向存在鄰接關(guān)系能夠更好地提取目標(biāo)。

為了保證分支間的鄰接方向是豎直的，定義了行段的概念，并利用行段獲取分支。

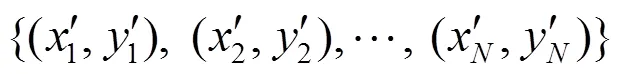
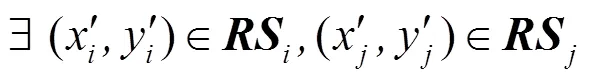
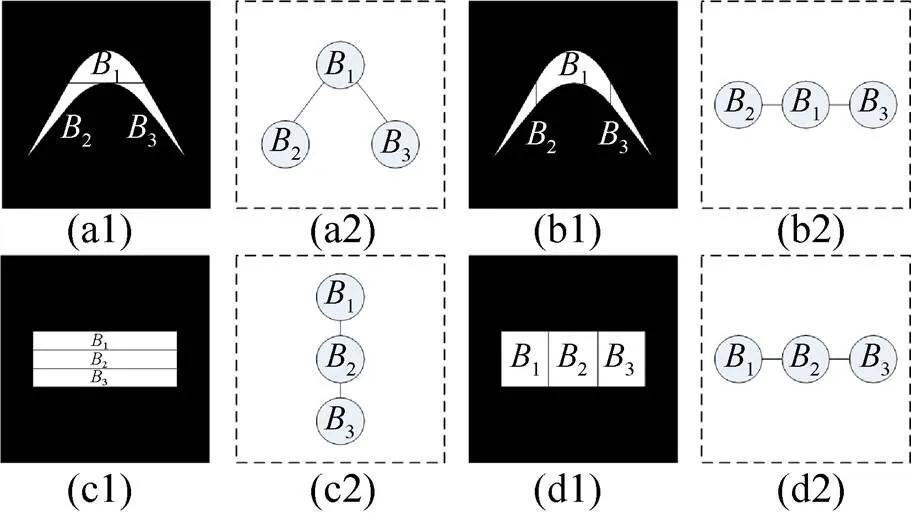
圖2 分支劃分示意圖((a1)和(a2)為豎直方向存在鄰接關(guān)系的雙曲波和鄰接空間；(b1)和(b2)為水平方向存在鄰接關(guān)系的雙曲波和鄰接空間；(c1)和(c2)為豎直方向存在鄰接關(guān)系的非雙曲波和鄰接空間；(d1)和(d2)為水平方向存在鄰接關(guān)系的非雙曲波和鄰接空間)

如圖3所示，圖中共包含9個數(shù)據(jù)點，由于數(shù)據(jù)左右位置無相鄰數(shù)據(jù)，因此無法構(gòu)成行段。數(shù)據(jù)，的橫坐標(biāo)順序相連，因此，構(gòu)成了一個行段1，同樣的，數(shù)據(jù)，和數(shù)據(jù)，，，分別構(gòu)成了2個行段2，3。對于行段1和3，由于1中數(shù)據(jù)，分別與3中數(shù)據(jù)，的橫坐標(biāo)相同，縱坐標(biāo)順序相連，因此1與3互為鄰接行段，而2與1，3中數(shù)據(jù)不相鄰，因此2沒有鄰接行段。由于行段間只在豎直方向才具有鄰接關(guān)系，因此將行段作為分支的基本單元能夠令分支間只在豎直方向存在鄰接關(guān)系。

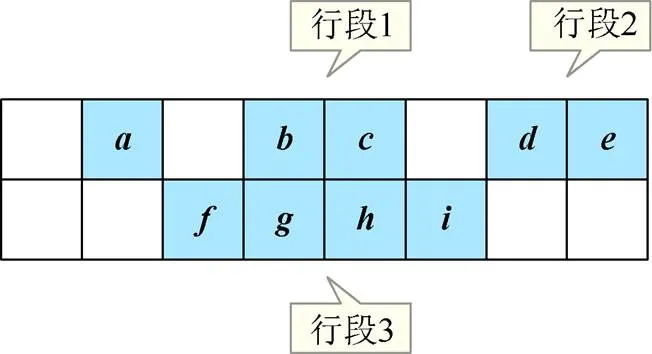
圖3 行段與鄰接行段示意圖

為了能夠準(zhǔn)確地獲得分支，定義了一個基于信息熵的距離度量。對于任意類別C，如果存在與其具有鄰接關(guān)系的類別C，則使用下式計算兩者間的距離

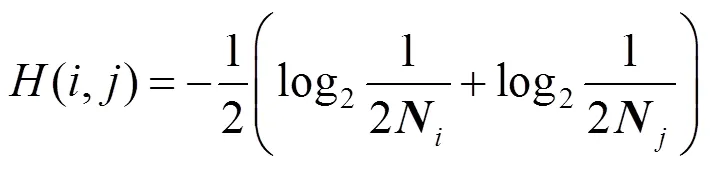
其中，N為C在C方向上相鄰類的數(shù)量；N為C在C方向上相鄰類的數(shù)量，并且如果C水平方向存在相鄰類或豎直方向存在多個相鄰類，同時C是C豎直方向的相鄰類，則=1，否則=0。

本文使用層次聚類算法對數(shù)據(jù)集進(jìn)行聚類，并將數(shù)據(jù)集中的每個像素看作一個單獨的類，即={1,2,···,C}，聚類后將中的每個類C看作一個分支B。層次聚類算法如下：

Algoritm: hierachical clustering based on information entropy Input: dataset D Define: dis(Ci,Cj) means calculating the distance between Ci and Cj using formula (1)，Dis(i) includes the distance of Ci and other classes Key =true WhileKey Key=false fori from 1 to D_Class_Num Searching classes that adjacent to Ci and comprising D′ for j from 1 to D′_Class_Num =dis(Ci,Cj) end =min(Dis(i)); =argmin(Dis(i)); if =min()and =argmin() combing Ci and Cj, update D Key=true end end end Output: dataset D with Ci

1.1.2 多標(biāo)簽聚類

層次聚類之后，構(gòu)造聚類結(jié)果的鄰接空間，構(gòu)造過程中將每個分支看作一個“節(jié)點”，如果2分支間存在鄰接行段，則連接對應(yīng)的2個節(jié)點。本文利用該空間獲取與雙曲波具有相同鄰接空間的像素子集，并為各子集中的分支分配標(biāo)簽，屬于相同像素子集的分支具有相同的標(biāo)簽，由于鄰接空間的結(jié)構(gòu)復(fù)雜多樣，因此同一分支可能會被分配多個標(biāo)簽。如圖4所示，對圖4(a)中的數(shù)據(jù)進(jìn)行層次聚類，將聚類結(jié)果中的每類看作一個分支，圖4(b)展示了聚類得到的8個分支{1,2,···,8}，根據(jù)分支的鄰接空間構(gòu)造多叉樹(圖4(c))，樹中共包含4個二叉分枝：{1,4,5}，{1,4,6}，{1,5,6}，{4,7,8}。對于任意二叉分枝，如果其孩子節(jié)點的數(shù)據(jù)量之和與父節(jié)點數(shù)據(jù)量的比例小于，則提取此二叉分枝。閾值的作用是去除噪聲過多的數(shù)據(jù)集合，通常是一個較小的值，如{1,5,6}中5，6包含數(shù)據(jù)量與1的比值如果小于閾值，那么此二叉分枝的形狀更傾向于直線型，不符合雙曲波的形狀特性，對于降低計算量，提高運算效率有重要意義。

值得注意的是，提取二叉分枝會受到大量的干擾，這些干擾可能來自于雜波和噪聲，也可能來自于其他雙曲波。

如圖5(a1)為2個有重疊部分的雙曲波，藍(lán)色區(qū)域表示提取到的二叉分枝。

圖5中紅色曲線為標(biāo)準(zhǔn)的擬合曲線，藍(lán)色曲線為最小二乘法的擬合結(jié)果，可以看出修整前數(shù)據(jù)的擬合誤差率較高(圖5(a2))，因為距離計算是根據(jù)數(shù)據(jù)與當(dāng)前迭代曲線的縱坐標(biāo)差值得到的。為了降低擬合誤差，使用單位矩陣修整各聚類結(jié)果，使用所有值等于1的單位矩陣，即

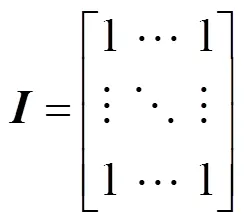
其中，矩陣的維度與分支中最底端行段所包含像素的數(shù)目相同，本文使用該矩陣與分支底端的像素進(jìn)行或運算以完善雙曲波像素集合，修整結(jié)果如圖5(b2)所示，修整后數(shù)據(jù)的擬合曲線更接近于標(biāo)準(zhǔn)的擬合曲線。

1.2 雙曲波提取

使用多標(biāo)簽層次聚類獲取的像素子集與雙曲波鄰接空間的結(jié)構(gòu)相同，本文使用最小二乘法和灰度共生矩陣提取了各子集的形狀和紋理特征，并結(jié)合兩特征進(jìn)行雙曲波提取。由于雙曲波的形狀均是開口向下的，可使用最小二乘法擬合像素子集，并利用擬合結(jié)果提取數(shù)據(jù)的形狀特征，即

擬合之后，以頂點所在列為中心，獲取其左右兩側(cè)到曲線之間都存在數(shù)據(jù)的行，記這些行的數(shù)據(jù)量之和為A。計算該數(shù)據(jù)集的置信度為

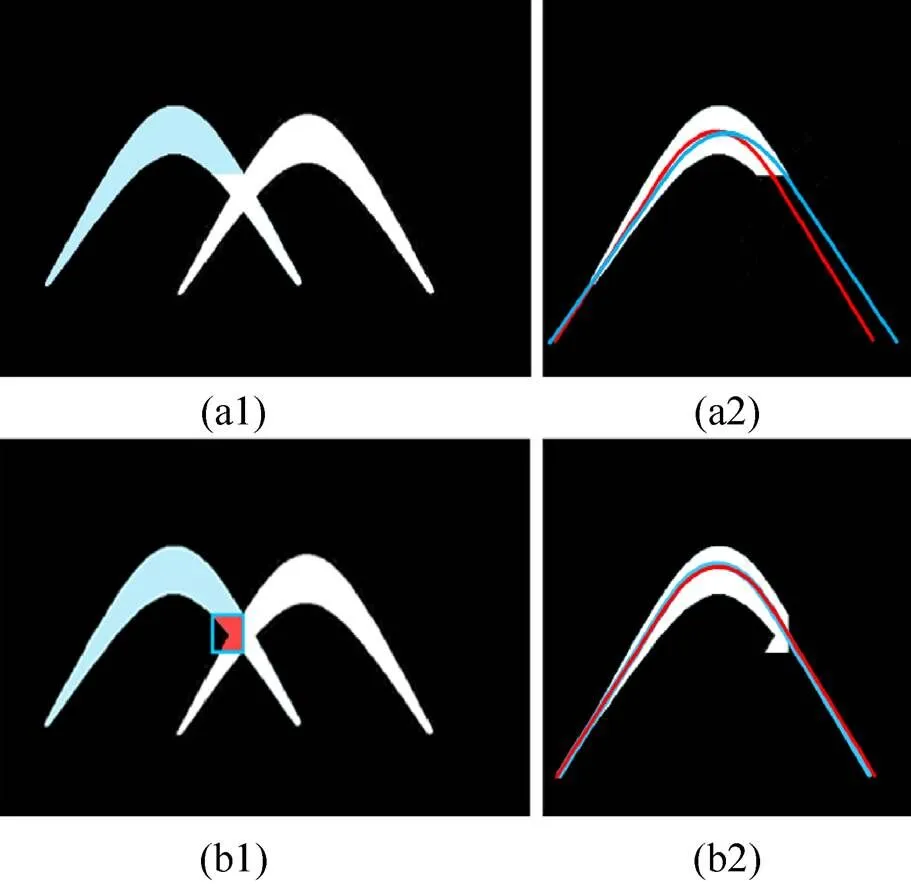
圖5 二叉分枝的修整效果比較((a1)和(a2)修整前的二叉分枝及其擬合結(jié)果；(b1)和(b2)修整后的二叉分枝及其擬合結(jié)果)

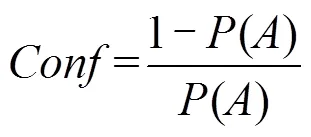
其中，()為曲線之間的各行的數(shù)據(jù)量之和與長度之和的比例。

為了更準(zhǔn)確地計算雙曲波置信度，使用多級閾值分割候選數(shù)據(jù)所在的矩形區(qū)域，并對各分割結(jié)果使用如下公式進(jìn)行聚類。聚類時順序選擇分割結(jié)果中的數(shù)據(jù)，其數(shù)據(jù)分配類別為

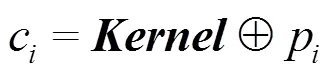
其中，p為當(dāng)前數(shù)據(jù)；為3階單位陣；?為運算。

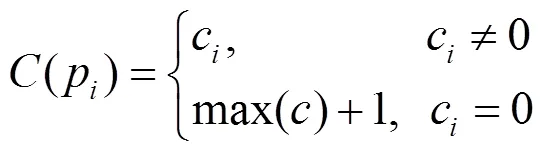
其中，max()為最大類別值。

聚類結(jié)束之后，從每個分割結(jié)果中提取與候選數(shù)據(jù)存在交集的類以構(gòu)成多級閾值空間，空間的層數(shù)等于閾值個數(shù)，每層的數(shù)據(jù)為各級閾值下提取的各個類。

計算空間中每層數(shù)據(jù)的置信度，取數(shù)據(jù)集的最終置信度為

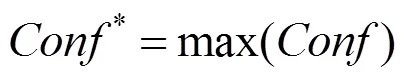
從多級閾值空間提取的特征能夠有效地判斷數(shù)據(jù)集的形狀，為了進(jìn)一步降低復(fù)雜紋理對上述特征的影響，通過ZHENG等[20]利用灰度共生矩陣判斷紋理方向的方法提取了一個二維特征。對于任意數(shù)據(jù)子集′，首先獲取其頂點，即

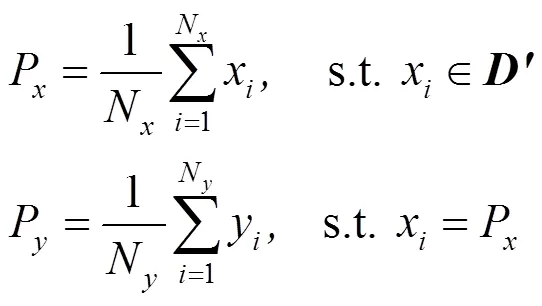
其中，N，N為滿足條件的數(shù)據(jù)量；P，P為頂點的橫縱坐標(biāo)。

以頂點為邊界，將數(shù)據(jù)切分為2個子數(shù)據(jù)集，計算其紋理方向為

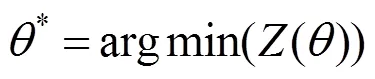
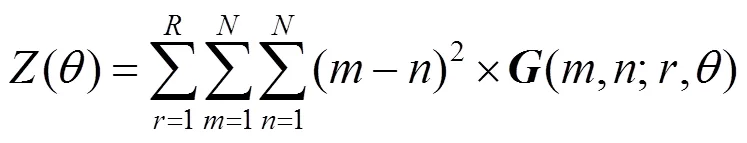
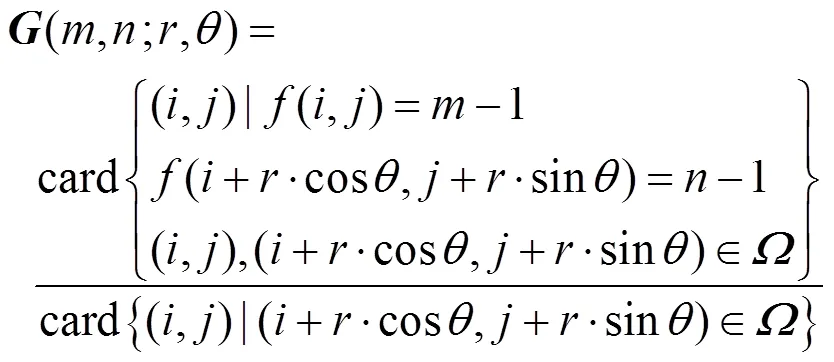
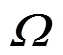
當(dāng)提取的每個雙曲波屬于不同的連通區(qū)域，部分雙曲波可能存在結(jié)構(gòu)不完整、碎片化和形狀異常等現(xiàn)象。為此，在提取各雙曲波*對應(yīng)的擬合曲線并進(jìn)行膨脹操作時，通過去除膨脹區(qū)域之外的雙曲波像素來修整雙曲波，并通過對修整后的目標(biāo)和膨脹區(qū)域進(jìn)行或運算來提高雙曲波的完整性。

2 實驗結(jié)果分析

為驗證MHCE算法的有效性，本文分析了MHCE每步的效果，并與其他算法進(jìn)行了性能比較。

2.1 實驗數(shù)據(jù)及預(yù)處理

使用實際應(yīng)用場景中采集的真實數(shù)據(jù)集進(jìn)行實驗分析。所用數(shù)據(jù)由627道數(shù)據(jù)組成，每道采樣點個數(shù)為400 (圖6)。圖中共包含5個雙曲波，分別屬于3個不同的地下管道。

圖6 GPR圖像

預(yù)處理過程采用引導(dǎo)濾波處理GPR圖像，并使用最大類間方差法對濾波后的圖像進(jìn)行二值化。其中引導(dǎo)濾波的引導(dǎo)圖為其本身，局部窗口半徑為16，正則化參數(shù)為0.01。結(jié)果如圖7所示。

圖7 預(yù)處理結(jié)果

2.2 多標(biāo)簽層次聚類算法分析

為驗證多標(biāo)簽層次聚類算法的有效性，分別對算法中基于信息熵的層次聚類和多標(biāo)簽聚類2個模塊進(jìn)行了分析。

2.2.1 基于信息熵的層次聚類效果分析

圖8為預(yù)處理后數(shù)據(jù)的層次聚類結(jié)果，其中相鄰的分支由2種不同的顏色表示。可以看出，圖中的每個雙曲波各包含3個分支，其構(gòu)成的鄰接空間呈等腰三角形。

圖8 基于信息熵的層次聚類結(jié)果

2.2.2 多標(biāo)簽聚類效果分析

層次聚類之后，使用多標(biāo)簽聚類獲取鄰接空間呈等腰三角形的像素子集。圖9為部分區(qū)域的多標(biāo)簽聚類結(jié)果。圖9(a)為圖8中的部分像素子集的放大圖，其中包含15個分支，構(gòu)造的鄰接空間如圖9(b)所示，空間中共包含4個二叉分枝，提取并修整這些二叉分枝作為多標(biāo)簽聚類的結(jié)果(圖9(c))，可見本方法提取的雙曲波和非雙曲波像素子集在形狀上存在較大差異，這可以提高雙曲波提取步驟的準(zhǔn)確率。圖10為二叉分枝提取的整體效果，結(jié)果表明此過程可以成功提取所有雙曲波，且所提取雙曲波兩側(cè)包含的噪聲量很少，證明使用該方法可以降低對雙曲波半徑的擬合誤差。

得到二叉分枝之后，需要對其進(jìn)行修整以完善雙曲波像素集合和提高擬合精度，效果如圖11所示，對雙曲波進(jìn)行修整之后，其兩側(cè)分支的像素集合得到了一定的完善。越完整的像素集合對于數(shù)據(jù)分析、三維建模等操作的幫助越大，并且可以提高對雙曲波的擬合精度。

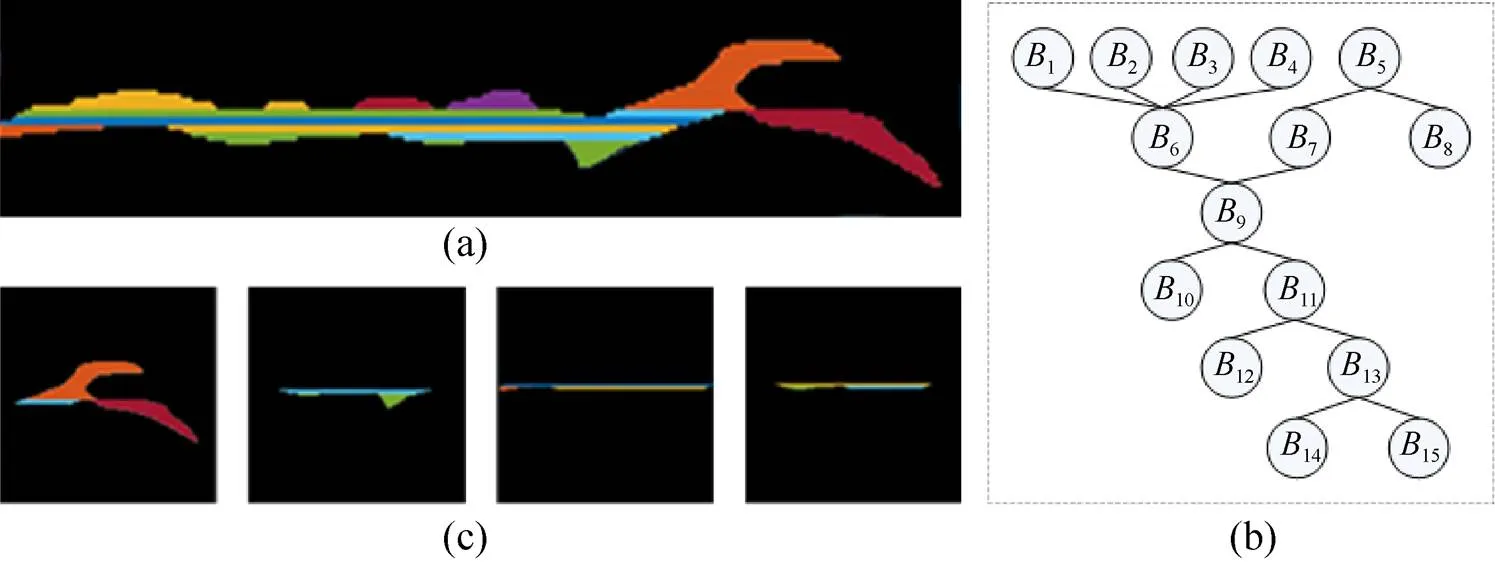
圖9 二叉分枝提取效果((a)多標(biāo)簽聚類結(jié)果；(b)鄰接空間；(c) 二叉分枝提取結(jié)果)

圖10 二叉分枝提取整體效果

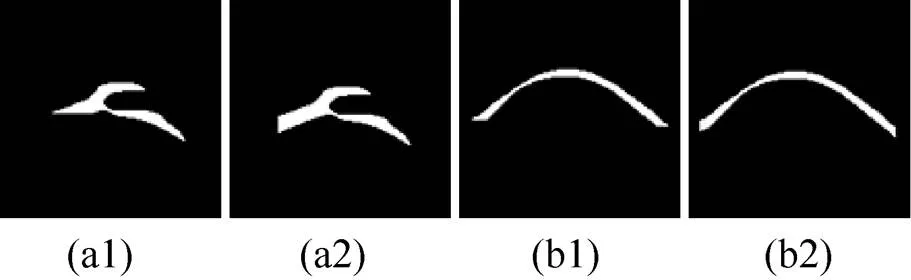
圖11 二叉分枝修整效果((a1)和(b1)修整前效果；(a2)和(b2)修整后效果)

為了準(zhǔn)確地評估修整過程對于雙曲波擬合精度的貢獻(xiàn)，使用最小二乘法比較了修整前后的擬合誤差，見表1，修整后的擬合誤差相對修整前有了一定幅度的降低，表明此過程可以提高對雙曲波的擬合精度。

此外，結(jié)果表明多標(biāo)簽層次聚類可以獲取雙曲波像素子集，并且受到鄰接空間的限制，兩側(cè)的噪聲對提取結(jié)果的影響很小，同時二叉分枝的修整過程可以完善像素集合，有助于數(shù)據(jù)分析、三維建模等操作，且擬合修整后的二叉分枝擁有更低的擬合誤差。

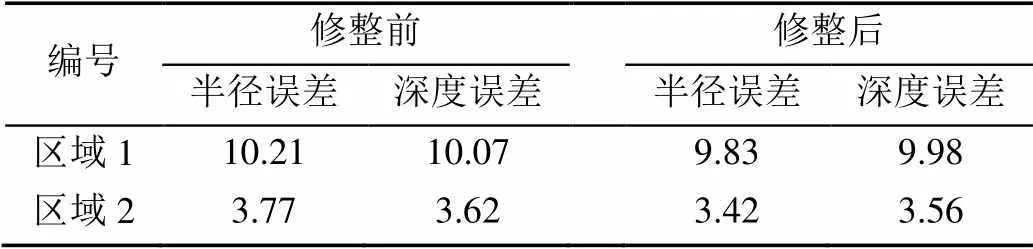
表1 二叉分枝修整擬合誤差(%)

2.3 雙曲波提取效果分析

圖12為MHCE算法提取到的初始雙曲波，可以看出圖中成功提取了5個雙曲波，但1號和3號區(qū)域中的雙曲波分別存在形狀異常和結(jié)構(gòu)不完整的情況。為此，在提取各雙曲波的擬合曲線時，可利用擬合曲線處理雙曲波碎片化、結(jié)構(gòu)不完整和形狀異常等問題。

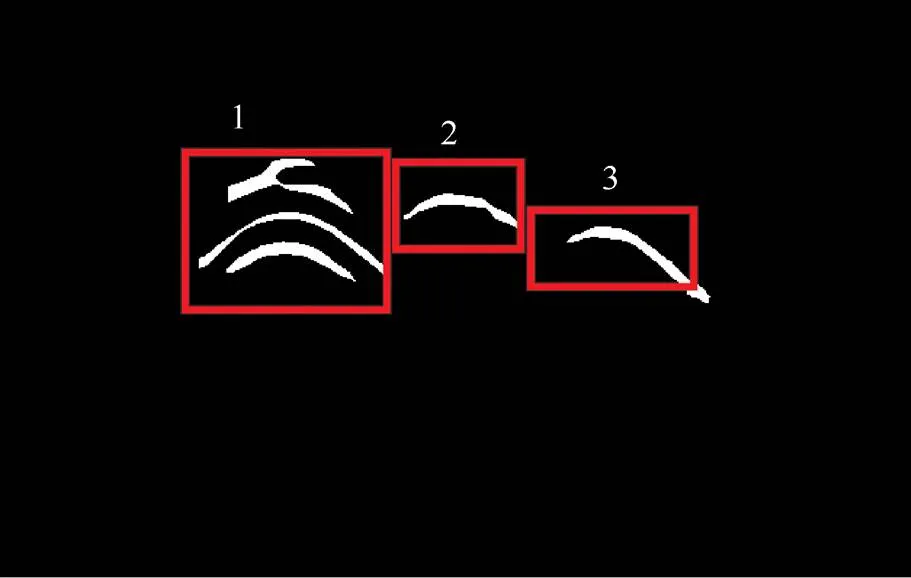
圖12 MHCE提取的初始雙曲波

得到擬合曲線之后，使用膨脹后的擬合曲線完善結(jié)構(gòu)不完整、形狀異常的雙曲波，結(jié)果如圖13所示，1號和3號區(qū)域中雙曲波的形狀被規(guī)范化，此外，本文使用SHIHAB和AL-NUAIMY[21]提出的方法比較了規(guī)范化前后的擬合誤差，見表2。結(jié)果顯示規(guī)范化前后對雙曲波的擬合誤差不大，且部分規(guī)范化后的擬合誤差呈現(xiàn)出輕微的下降趨勢，表明MHCE可以提取規(guī)范化的雙曲波，且規(guī)范化操作對擬合精度的影響較小。

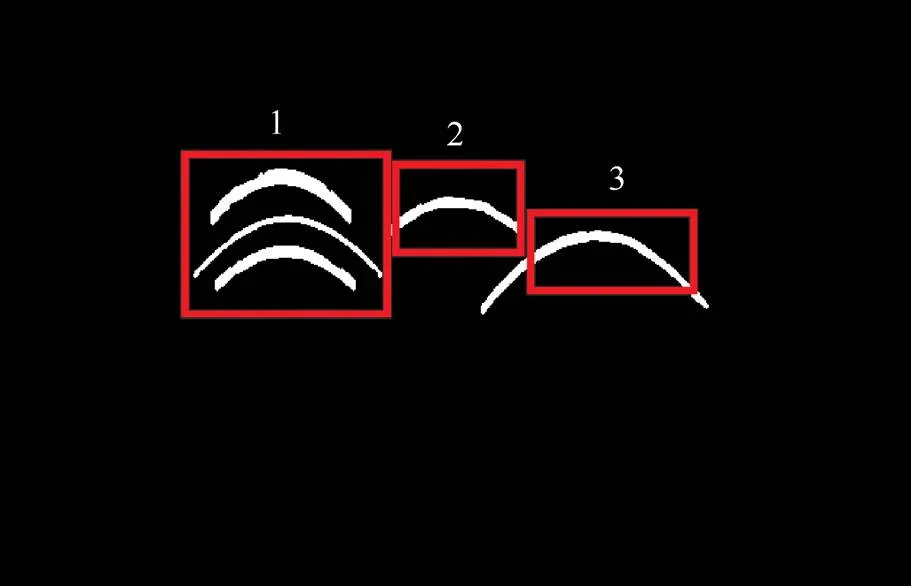
圖13 MHCE的提取結(jié)果

2.4 MHCE整體性能分析

為了更準(zhǔn)確地評價MHCE算法的性能。本文在預(yù)處理后的二值圖(圖7)中使用C3[15]，OSCA[17]，Hough[14]提取雙曲波，并與MHCE算法的性能進(jìn)行了比較。圖7中包含的5條雙曲波分別屬于4個不同的類型，如3號和4號雙曲波周圍只含有少量的噪聲。1號和2號雙曲波周圍含有較多的噪聲，其中1號周圍的噪聲多集中于上方和左側(cè)，2號周圍的噪聲則主要分布在左右兩側(cè)。此外，5號雙曲波左側(cè)分支擁有的像素數(shù)量較少，增加了雙曲波提取的難度。圖中雙曲波類型復(fù)雜多樣，因此使用該圖進(jìn)行評價有較強(qiáng)的說服力。本節(jié)比較了各算法的擬合精度和相應(yīng)的運行時間，為保證實驗結(jié)果的有效性，所有算法均在同一臺計算機(jī)中完成，計算機(jī)使用的CPU為Intel i7，內(nèi)存為16 G。結(jié)果見表3，表中的空白區(qū)域表示對應(yīng)的算法沒有成功提取到相應(yīng)雙曲波。

在4種算法中Hough的擬合時間最長，圖14展示了設(shè)置曲率在[50，110]之間時，擬合時間和步長之間的關(guān)系(本實驗設(shè)置Hough步長為1)。可以看出隨著步長的減小，擬合時間會逐漸增加。

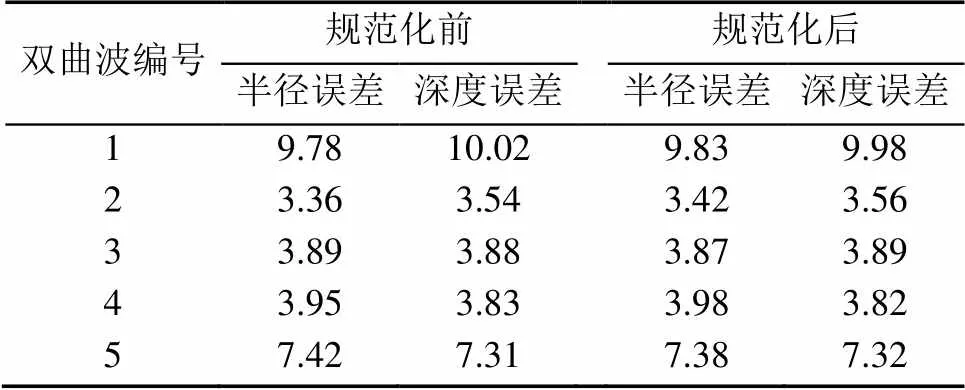
表2 規(guī)范化前后的擬合誤差比較(%)

表3 MHCE與C3，OSCA和Hough方法的擬合誤差(%)及時間(s)比較

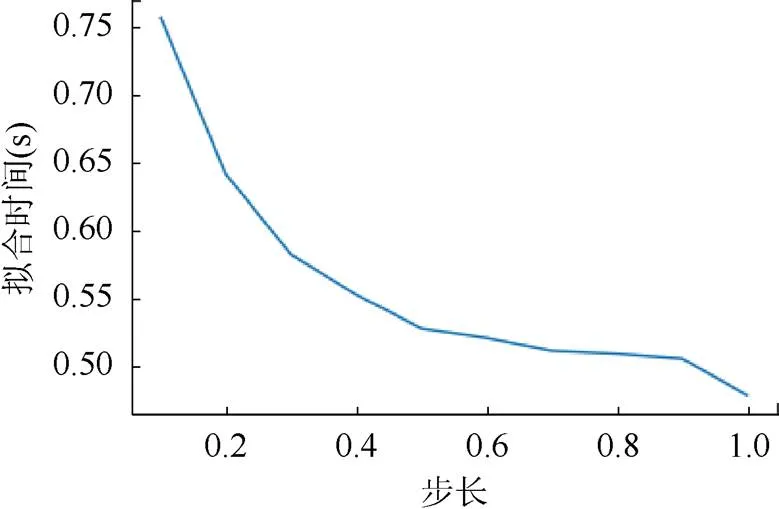
圖14 Hough步長與擬合時間的關(guān)系

本節(jié)還比較了步長和擬合誤差的關(guān)系，如圖15所示，結(jié)果表明擬合誤差與步長之間不存在正(負(fù))相關(guān)關(guān)系，且擬合誤差對步長比較敏感，同時設(shè)定一個擬合誤差較低的參數(shù)，可能會導(dǎo)致較高的時間消耗，這增加了該方法在實際應(yīng)用中的難度。

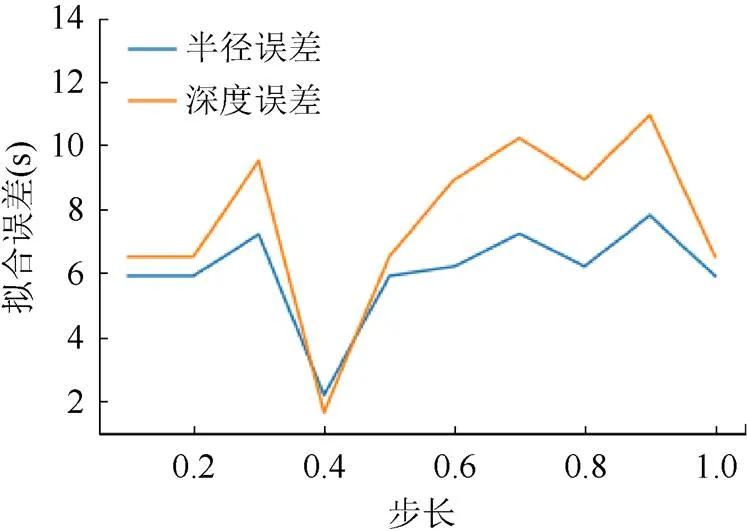
圖15 Hough步長與擬合誤差的關(guān)系

此外，根據(jù)表3中的擬合誤差可知，MHCE，C3和OSCA對3號和4號雙曲波的擬合精度均較高。但當(dāng)周圍存在較多噪聲時，如1號和2號雙曲波，OSCA和C3的提取效果受到了較大影響，其中OSCA無法成功提取1號雙曲波，且C3和OSCA對1號和2號雙曲波的半徑擬合誤差較高，但MHCE可以成功提取這2個雙曲波，且半徑擬合誤差的增長幅度小于OSCA與C3。這是由于OSCA在聚類過程中考慮了雙曲波間存在交集的情況，使得該算法在聚類過程中可以去除更多的雜波和噪聲，但當(dāng)噪聲增多時會影響所提取雙曲波的形狀，降低了擬合精度，并影響了該算法的識別率。C3算法根據(jù)列間的連接情況初步聚類，并從聚類結(jié)果的波谷處將其分裂為多個子類以提高聚類精確度，但當(dāng)雙曲波兩側(cè)存在噪聲且未形成波谷時，部分噪聲會被誤識為雙曲波像素，降低了擬合精度。MHCE在聚類過程中根據(jù)鄰接空間的結(jié)構(gòu)獲取像素子集，降低了丟失目標(biāo)的幾率和子集中噪聲的比例，提高了算法的魯棒性和對提取結(jié)果的擬合精度，因此雙曲波兩側(cè)的噪聲對其識別率和擬合精度的影響較小。

最后，本節(jié)比較了C3，OSCA和MHCE的識別率和誤識數(shù)量，見表4。OSCA和C3出現(xiàn)了丟失目標(biāo)和誤識目標(biāo)的情況，但MHCE可以成功提取4種類型的雙曲波，且未將其他雜波或噪聲誤識為雙曲波。這是由于擁有相同鄰接空間的雙曲波和非雙曲波子集在形狀或紋理上差異較大，因此，本算法通過結(jié)合多標(biāo)簽層次聚類和紋理及形狀約束進(jìn)行雙曲波提取可以成功降低誤識數(shù)量并提高算法的識別率。

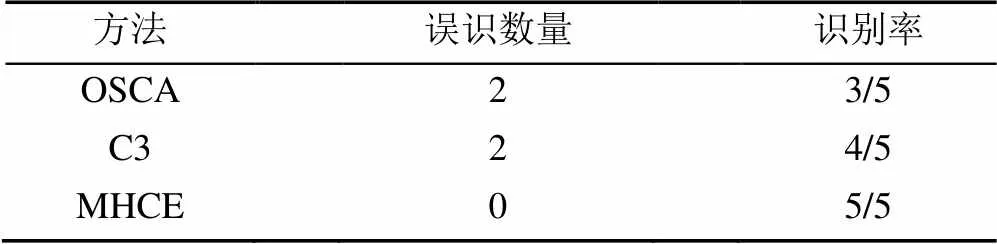
表4 MHCE與C3，OSCA的比較

3 結(jié)束語

針對真實環(huán)境中提取的雙曲波往往存在結(jié)構(gòu)不完整、碎片化和形狀異常等問題，提出了一個基于多標(biāo)簽層次聚類的雙曲波提取方法MHCE。該方法將信息熵融入到層次聚類中，結(jié)合層次聚類的鄰接空間構(gòu)造了多標(biāo)簽層次聚類算法，并根據(jù)聚類結(jié)果的擬合形狀和紋理方向提取雙曲波。MHCE可以在真實GPR圖像中進(jìn)行雙曲波提取，擁有較高的準(zhǔn)確率且提取的雙曲波具有較完整的波形。該方法基于無監(jiān)督學(xué)習(xí)進(jìn)行雙曲波提取，相比準(zhǔn)確性和魯棒性較高的基于區(qū)域特征(如HOG，Haar等)的有監(jiān)督學(xué)習(xí)方法，MHCE節(jié)省了樣本準(zhǔn)備的時間消耗。同時，該方法受鄰域范圍和形狀的影響較小，無需固定所提取的雙曲波形狀，降低了提取結(jié)果中的噪聲比例。此外，提取結(jié)果中不同的雙曲波屬于不同的連通區(qū)域，可直接利用最小二乘法擬合并獲得較準(zhǔn)確的雙曲波參數(shù)。

[1] BATRAKOV D O, ANTYUFEYEVA M S, ANTYUFEYEV O V, et al. GPR application for the road pavements surveys[C]//2017 IEEE Microwaves, Radar and Remote Sensing Symposium (MRRS). New York: IEEE Press, 2017: 81-84.

[2] SLOB E, SATO M, OLHOEFT G. Surface and borehole ground-penetrating-radar developments[J]. Geophysics, 2010, 75(5): 75A103-75A120.

[3] SOKOLOV K O, PRUDETCKII N D, FEDOROVA L, et al. GPR investigation of ice-filled cracks in loose deposits[C]//2018 17th International Conference on Ground Penetrating Radar (GPR). New York: IEEE Press, 2018: 1-4.

[4] 謝昭暉, 李金銘. 我國探地雷達(dá)的應(yīng)用現(xiàn)狀及展望[J]. 工程勘察, 2007, 35(11): 71-75. XIE Z H, LI J M. Application status and prospect of ground penetrating radar in China[J]. Engineering Survey, 2007, 35(11): 71-75 (in Chinese).

[5] SHEBALKOVA L, MARKOV M, ROMODIN V. Broadband antenna for ground penetrating radar application in soil[C]//2018 IOP Conference Series: Earth and Environmental Science (EES). England: IOP Publishing, 2018:012060.

[6] TERRASSE G, NICOLAS J M, TROUVE E, et al. Application of the curvelet transform for clutter and noise removal in GPR data[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2017, 10(10): 4280-4294.

[7] TORRIONE P A, MORTON K D, SAKAGUCHI R, et al. Histograms of oriented gradients for landmine detection in ground-penetrating radar data[J]. IEEE Transactions on Geoscience and Remote Sensing, 2014, 52(3): 1539-1550.

[8] TBARKI K, BEN SAID S, KSANTINI R, et al. Landmine detection improvement using one-class SVM for unbalanced data[C]//2017 International Conference on Advanced Technologies for Signal and Image Processing (ATSIP). New York: IEEE Press, 2017: 1-6.

[9] GIOVANNESCHI F, MISHRA K V, GONZALEZ-HUICI M A, et al. Dictionary learning for adaptive GPR landmine classification[J]. IEEE Transactions on Geoscience and Remote Sensing, 2019, 57(12): 10036-10055.

[10] MISSAOUI O, FRIGUI H, GADER P. Land-mine detection with ground-penetrating radar using multistream discrete hidden Markov models[J]. IEEE Transactions on Geoscience and Remote Sensing, 2011, 49(6): 2080-2099.

[11] ZHANG X P, BOLTON J, GADER P. A new learning method for continuous hidden Markov models for subsurface landmine detection in ground penetrating radar[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2014, 7(3): 813-819.

[12] MANANDHAR A, TORRIONE P A, COLLINS L M, et al. Multiple-instance hidden Markov model for GPR-based landmine detection[J]. IEEE Transactions on Geoscience and Remote Sensing, 2014, 53(4): 1737-1745.

[13] MAAS C, SCHMALZL J. Using pattern recognition to automatically localize reflection hyperbolas in data from ground penetrating radar[J]. Computers & Geosciences, 2013, 58: 116-125.

[14] SHARMA P, KUMAR B, SINGH D, et al. Non-metallic pipe detection using SF-GPR: a new approach using neural network[C]//2016 IEEE International Geoscience and Remote Sensing Symposium (IGARSS). New York: IEEE Press, 2016: 6609-6612.

[15] DOU Q X, WEI L J, MAGEE D R, et al. Real-time hyperbola recognition and fitting in GPR data[J]. IEEE Transactions on Geoscience and Remote Sensing, 2017, 55(1): 51-62.

[16] KAFEDZISKI V, PECOV S, TANEVSKI D. Target detection in SFCW ground penetrating radar with C3 algorithm and hough transform based on GPRMAX simulation and experimental data[C]//2018 25th International Conference on Systems, Signals and Image Processing (IWSSIP). New York: IEEE Press, 2018: 1-5.

[17] ZHOU X R, CHEN H H, LI J L. An automatic GPR B-scan image interpreting model[J]. IEEE Transactions on Geoscience and Remote Sensing, 2018, 56(6): 3398-3412.

[18] HE K, SUN J, TANG X. Guided image filtering[C]// European Conference on Computer Vision. Heidelberg: Springer, 2010: 1-14.

[19] WANG Y. Improved OTSU and adaptive genetic algorithm for infrared image segmentation[C]//2018 Chinese Control and Decision Conference (CCDC). New York: IEEE Press, 2018: 5644-5648.

[20] ZHENG G, LI X F, ZHOU L Z, et al. Development of a gray-level Co-occurrence matrix-based texture orientation estimation method and its application in sea surface wind direction retrieval from SAR imagery[J]. IEEE Transactions on Geoscience and Remote Sensing, 2018, 56(9): 5244-5260.

[21] SHIHAB S, AL-NUAIMY W. Radius estimation for cylindrical objects detected by ground penetrating radar[J]. Subsurface Sensing Technologies and Applications, 2005, 6(2): 151-166.

Hyperbola extraction method based on multi-label hierarchical clustering algorithm of GPR images

LI Wen-sheng, YUAN Da, MIAO Cui, WANG Dong-yu

(Key Laboratory of Intelligent Information Processing, Shandong Technology and Business University, Yantai Shandong 264005, China)

Hyperbola extraction in ground penetrating radar (GPR) images is an important feature to analyze the location and structure of underground objects. However, there are often some problems with the extracted hyperbola, such as incomplete structure, fragmentation, and shape anomalies, caused by the interference of noise and clutter that are typical of real environments. These issues are not conducive to the subsequent quantitative operations, such as data analysis and 3D modeling. In this context, this paper proposed a multi-label hierarchical clustering-based hyperbola extraction method (MHCE) for the hyperbola extraction of GPR images. Firstly, through evaluating the stability between pixel neighborhoods by the means of information entropy, an information entropy-based distance method was constructed to conduct the hierarchical clustering algorithm. Next, a multi-label clustering method was proposed based on the adjacency space of the clustering results, so as to reduce the influence of clutter and noise on hyperbola extraction. Finally, the hyperbola was extracted combined with the fitting shape and texture orientation of the multi-label clustering results. The experimental results show that this method is robust for GPR images and can be used to obtain the shape and position parameters of a normalized hyperbola.

ground penetrating radar image; hyperbola; information entropy; multi-label hierarchical clustering algorithm; robustness

TP 391

10.11996/JG.j.2095-302X.2020030399

A

2095-302X(2020)03-0399-10

2019-12-11；

2020-01-23

山東省重點研發(fā)計劃項目(2019GGX101040)

李文生(1994-)，男，山東淄博人，碩士研究生。主要研究方向為探地雷達(dá)數(shù)據(jù)分析與模式識別。E-mail：1700812107@sdtbu.edu.cn

原 達(dá)(1968-)，男，遼寧建昌人，教授，博士，碩士生導(dǎo)師。主要研究方向為探地雷達(dá)數(shù)據(jù)分析、數(shù)據(jù)可視化等。E-mail：ydccec@126.com