基于蒙特卡洛模擬的井眼軌跡測斜計算方法對比分析研究

陳庚緒，樊 銳，李紅星，王新剛，白雪龍，王越支

(1長江大學石油工程學院 2中國石油集團渤海鉆探工程有限公司第二鉆井工程分公司 3中海油服油技塘沽作業公司)

井眼軌跡測斜計算方法很多，常見的有平均角法、校正平均角法、平衡正切法、最小曲率法、曲率半徑法和弦步法等，不論哪種方法都是將測點之間的測段假定為某種特定的線段，但是測段間真實客觀存在的井眼軌跡形狀是無法預知的，故測斜計算得到的井眼軌跡與真實客觀存在的井眼軌跡必然不相同。針對井眼軌跡測斜計算誤差問題，陳煒卿、管志川等學者通過構造理論參考曲線，對不同測斜計算方法計算的平均井眼位置進行了大樣本空間對比分析，得出所有測斜計算方法表現出來的誤差特性都很相似的結論，并用統一的解析式表示了所有的測斜計算方法所產生的誤差概率密度函數，但是誤差和不確定度是兩個不同的概念，他們沒有從不確定度的角度去進一步分析[1-2]。

最小曲率法是建立在如下假設基礎上的：①最小曲率法是基于分段近似，假設測點之間的曲率為定值;②最小曲率法是一階連續的，但它在二階導數和三階導數中表現出不連續性。對于給定的一組測點，實際井眼軌跡可能是曲線段和直線段的混合曲線，而不是連續的曲線，就算是先進的旋轉導向工具(RSS)也不能鉆出連續曲線。在眾多井眼軌跡計算方法中，樣條曲線法基于線性代數方法，對于一階，二階和三階都是連續的。樣條曲線法能有效使得給定測段的曲率和曲率變化率連續(二階和三階)[3-6]。

圖1顯示了用最小曲率法計算兩測點之間的三種可能的井眼軌跡，由與測斜數據相匹配的圓弧表示。中間的圓弧為最小曲率法計算的井眼軌跡，因測點間可能是復合鉆進和滑動鉆進交叉進行且兩者之比無法確定，故另外兩條井眼軌跡不同于用最小曲率法計算的井眼軌跡，從而導致井眼曲率(二階)不連續。這種不連續性導致由每個圓弧的半徑表示的恒定曲率半徑產生了差異。最小曲率法與樣條曲線法的區別是一個只能保證函數值連續，另一個除了保證函數值連續還保證它的導數也連續。

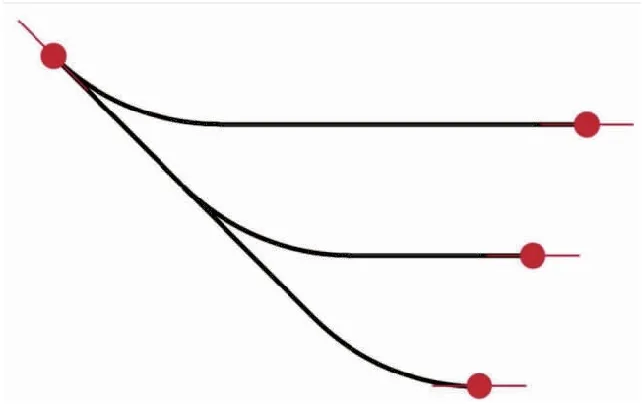
圖1 兩測點間滑動距離不同對測段的影響

一、井眼軌跡計算方法的蒙特卡洛模擬

蒙特卡洛模擬是基于概率統計的一種算法[7]，若需模擬井眼軌跡誤差不確定度，需要先建立概率統計模型，其次確定模型中誤差變量數據的分布，然后根據誤差變量的精度要求確定模擬抽樣次數，最后在隨機抽樣產生結果的基礎上實現概率統計分析，隨機抽樣的次數越多，井眼軌跡位置越逼近真實值。在本研究中，井眼軌跡測斜計算方法即概率統計計算模型，模型中的誤差變量為井斜角誤差、方位角誤差和井深誤差。本研究主要圍繞最小曲率法、曲率半徑法和樣條曲線法展開蒙特卡洛模擬分析。

1.井眼軌跡測斜計算模型

最小曲率法和曲率半徑法是常見的井眼軌跡測斜計算方法，這兩種計算方法不再累述。樣條曲線法假設井眼軌跡是一個由三次多項式組成的函數，且函數一階導、二階導在所有測點都是連續的，其測斜計算模型為[7]：

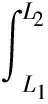
(1)

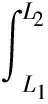
(2)

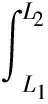
(3)

式(1)～式(3)中：ΔV、ΔN和ΔE—分別為垂深、北坐標和東坐標增量，m；I和A—井斜角和方位角，°；ΔI和ΔA—井斜角和方位角增量，°；ΔL—測段長，m。

2.井眼軌跡誤差變量分布及精度的確定

1999年威廉姆森對于各種測量工具和測量類型，在特定井眼條件下給定誤差的加權函數，測量誤差得到了很好的理解和建模。加權函數考慮了誤差源對方位角和井斜角的影響，測量工具通常根據一個標準偏差來反應測量精度，加權函數對每個工具都是唯一的，對于這一分析，測得的深度、井斜角和方位角的在一西格瑪精度下的標準偏差分別為0.3 m、0.25°和0.36°(即σH=0.3，σI=0.25，σA=0.36)，整口井的標準偏差為常量。圖2為標準正太分布圖。

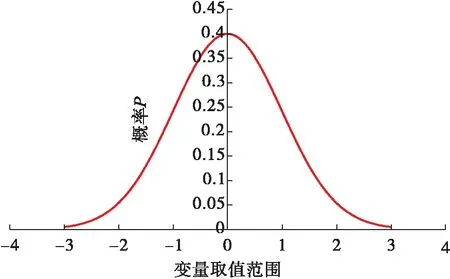
圖2 標準正態分布

井眼軌跡空間位置用隨機正態分布得到的測深、井斜角和方位角進行模擬即可得井眼軌跡不確定性范圍散點圖。

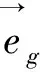
(4)

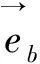
(5)

式中：I—井斜角，°；A—方位角，°。

3.三種井眼軌跡測斜計算方法的蒙特卡洛模擬結果

本研究是比較不同井眼軌跡測斜計算方法在假設分布條件下所產生的井眼位置不確定性，井眼軌跡測斜計算誤差指的就是由某種測斜計算方法得到的井眼位置與真實井眼位置在相同測深處的井眼位置之間的距離。因此，首先需要定義真實井眼位置或者一個可以作為真實值的測量值。自動尋北高分辨率連續速率陀螺儀不受磁場干擾，而最小曲率法是目前井眼軌跡計算的行業標準，因此，根據陀螺測量數據用最小曲率法計算的井眼位置被認為是比較真實的井眼軌跡，可將其作為擬定真值[8]。

由于測點之間為曲線的假設相對來說更加符合井眼軌跡的實際情況，故本文選取中海油遼東灣某井的隨鉆測量和陀螺測量數據，就最小曲率法、曲率半徑法和樣條曲線法三種井眼軌跡計算方法展開了蒙特卡洛模擬分析研究。圖3為三種方法的對比圖。

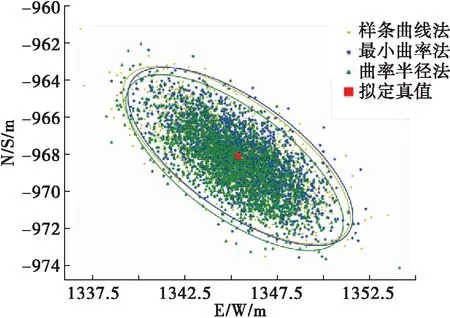
圖3 三種方法井眼軌跡位置的蒙特卡洛模擬對比

二、三種井眼軌跡計算方法蒙特卡洛模擬統計對比分析

在上述計算實例中，樣條曲線法較最小曲率法和曲率半徑法在井眼軌跡不確定誤差橢圓/球方面有了微小的變化。使用樣條曲線法計算得到的井眼軌跡不確定誤差橢圓/球的大小略大于最小曲率法和螺旋圓柱法，但是樣條曲線法計算得到的不確定性誤差橢圓/球的中心位置卻更集中于擬定真值附近。若忽略置信區間的影響，則樣條曲線法計算得到的井眼軌跡位置的不確定度因接近擬定真值而較最小曲率法和曲率半徑法分別降低了約78%和91%。具體結果見表1和表2。

表1 蒙特卡洛模擬在井底測點的統計分析

表2 蒙特卡洛模擬在井底測點的不確定度分析

與1 m間隔的高分辨率測量得到的擬定真值相比，無論采用何種井眼軌跡計算方法得到的不確定度誤差橢球都會在橢球中心處發生偏移。原因是系統誤差未經過充分修正且測點之間的高狗腿度很難精確的去確定。圖4是井眼坐標系下的井眼軌跡誤差橢球各半軸的概率密度圖。可以看出，30 m測量間隔計算的井眼軌跡誤差橢球中心之間的差異顯示了置信區間和概率密度之間的區別。

圖4 井眼坐標系下井底測點誤差橢球各半軸的概率密度圖

三、結論與建議

(1)井眼軌跡測斜計算方法的蒙特卡羅模擬表明，各種井眼軌跡測斜計算方法在誤差橢球不確定度表征上的差異不大是可以忽略不計的。忽略置信區間的影響，針對30 m的標準測量間隔距離，樣條曲線法計算的井眼軌跡位置更準確，但與最小曲率法和曲率半徑法一樣受到系統誤差的影響。

(2)計算井眼軌跡位置不確定度的大小不僅受各種誤差因素(標準偏差)的影響，還取決于誤差模型(本文為井眼軌跡測斜計算方法)，蒙特卡洛計算機模擬簡化了繁瑣的計算過程，使得井眼軌跡測斜計算方法對比起來更加簡單明了。

(3)針對最小曲率法計算的井眼軌跡，可以采取相應措施來大大提高測量的準確性，比如在滑動鉆進之間的中點處進行測量或在已知的狗腿角較大的井段加密測量，這都將對井眼軌跡位置和井眼位置產生顯著影響。