PVA-ECC徐變性能試驗研究

王玉清, 劉 瀟, 劉曙光, 孫 亮

(1.內蒙古工業大學 土木工程學院, 內蒙古 呼和浩特 010051; 2.內蒙古工業大學 礦業學院, 內蒙古呼和浩特 010051; 3.國網內蒙古東部電力有限公司興安供電公司, 內蒙古 烏蘭浩特 137400)

在持續恒定荷載作用下,水泥基材料的變形隨時間延長而不斷增長的現象稱為徐變.徐變是水泥基材料的重要特性,一般徐變變形比瞬時彈性變形大1～3倍.徐變的存在會引起預應力混凝土結構的預應力損失,使結構構件的變形增加,在構件中引起應力重分布等,對結構構件在長期荷載作用下的開裂、變形等性能有較大影響.1907年,Hatt[1]發現了混凝土材料在應力不增加的情況下變形會緩慢增長的現象,并稱之為徐變.同年,美國材料試驗學會(ASTM)首先報道了鋼筋混凝土梁的徐變.1917年,Smith[2]在美國混凝土學會(ACI)雜志上發表了混凝土徐變與徐變恢復的試驗結果.直到1931年,Davis等[3]對混凝土徐變性能進行了系統研究之后,大家才對混凝土的徐變性能有了較為明確的認識.100多年來,國內外學者對混凝土徐變進行了大量的研究,并取得一些成果[4-7].一般認為水泥基材料徐變的產生與其中膠凝體、水分的遷移等有關;影響水泥基材料徐變的因素較多,主要有原材料的性質及其含量、加荷齡期、加荷應力比、持荷時間、養護條件、環境相對溫濕度和幾何尺寸等[8-14].但是到目前為止,對混凝土等水泥基材料徐變機理的認識尚不夠深入,理論也不夠完善.

同時,隨著人們對結構功能和材料性能要求的不斷提高,近年來對改性水泥基材料的研究與應用日益增多,纖維水泥基材料越來越得到重視,聚乙烯醇纖維增強水泥基復合材料(engineered cementitious composite with polyvinyl alcohol fiber,PVA-ECC)便是其中之一.聚乙烯醇(PVA)纖維具有高強、高彈性模量、耐酸、耐堿等優點,且與聚乙烯(PE)等纖維相比,價格更加低廉.將其添加到水泥基材料中,可以大大改善基材性質,提高基材的抗裂、抗滲、抗沖擊韌性及耐久、耐高溫、耐腐蝕等性能,故近年來受到工程界人士的關注,成為工程材料研究的熱點之一[15-17].但目前國內外學者對于PVA-ECC材料短期力學性能的研究較多,對其長期性能的研究主要集中在耐久性、侵蝕等方面,而對PVA-ECC材料徐變性能的研究尚少.在現有的研究成果中,Boshoff等[18-19]、Kong等[20]將PVA-ECC假定為一種均質材料,并進行了拉伸荷載作用下的徐變性能研究,提出了PVA-ECC拉伸徐變模型;Benny等[21]根據PVA-ECC材料短期力學性能預測了高拉應力下的徐變;張為民等[22]對PVA纖維增強水泥基復合材料的軸壓徐變性能進行了研究,得出了纖維摻量大于1%時,徐變系數隨纖維摻量的變化規律.另外,部分學者研究了纖維混凝土的徐變性能,如于俊超[23]研究了加入不同種類纖維混凝土的徐變性能,得出了纖維混凝土試件徐變度隨齡期的變化關系;何智海等[24-25]研究總結了2種PVA纖維摻量及減縮劑對高強混凝土徐變性能的影響規律,發現在所研究纖維摻量范圍內,PVA纖維的摻入提高了混凝土的徐變系數,摻用過量的纖維顯著增大了材料的徐變系數.在以上研究中,所考慮工況比較單一,研究不夠深入,成果也不夠豐富.除此之外,未見到其他公開發表的關于PVA-ECC徐變性能的研究文獻.而PVA-ECC結構構件的長期力學性能分析、裂縫及變形計算、預應力損失計算、非線性有限元分析等又需要以材料徐變性能的研究結果為基礎[26-27].因此,PVA-ECC材料徐變性能研究成果的匱乏阻礙了PVA-ECC材料后續其他性能的研究及工程應用.

基于上述情況,本文對7組不同纖維摻量和加荷齡期下的PVA-ECC試件進行了恒定軸壓作用下的徐變試驗研究,結合國內外對水泥基材料徐變性能的研究理論與計算方法,確定了能夠反映PVA-ECC材料徐變性能的評價指標,并根據試驗結果提出了徐變評價指標的估算模型.以期為PVA-ECC構件的徐變計算及構件設計方法的制定提供參考,從而促進PVA-ECC材料的工程應用.

1 試驗概況

1.1 試驗設計

本試驗參照GB/T 50082—2009《普通混凝土長期性能和耐久性能試驗方法標準》,共設計7組PVA-ECC試件.由于無粗骨料,按照砂漿徐變試驗的尺寸要求,確定采用尺寸為40mm×40mm×160mm的棱柱體試件,每組試件分為徐變和收縮2類,每類試件各2個且每組試件均為同一批次制作,收縮試件作為對比試件以得到徐變試件在同一時期的收縮值.試驗加載應力水平均為0.4fc,其中fc是尺寸為40mm×40mm×160mm的棱柱體試件28d抗壓強度.PVA-ECC材料配合比為m(水泥)∶m(粉煤灰)∶m(標準砂)∶m(水)∶m(增稠劑)∶m(消泡劑)∶m(增塑劑)∶=600∶400∶600∶260∶1∶2∶20,纖維摻量(體積分數,以PVA-ECC材料總體積計)為0%、1.0%、1.5%、2.0%.纖維采用日本Kuraray公司生產的REC15型PVA纖維,其性能參數見表1.

表1 PVA纖維性能

1.2 加載方案及數據采集

所有試件均在標準養護室中養護至7d齡期后移入徐變試驗環境,收縮試件與徐變試件始終放置于同一環境中.試件在實驗室放置到14、28、90、180d 時進行加載,在對徐變試件加載的過程中,收縮試件自然擱置于臺面,下墊塑料布,以避免試件下部與臺面進行水分交換.徐變試驗環境為實驗室常溫環境,加載裝置如圖1所示,加載通過機械千斤頂在試件底部持力.加載設備采用天津多維克貿易有限公司生產的20t機械千斤頂,力值監控采用力傳感器連接測力儀進行,其中傳感器采用廣州電測生產的輪輻式yzc-219傳感器,測力儀采用WTB2116C多通道測力儀,試驗加載程序參照GB/T 50152—2012《混凝土結構試驗方法標準》執行.試驗中涉及徐變及收縮的變形均采用電測法粘貼應變片進行測量,在試件的1對平行側面中部貼縱向應變片,以量測試件的縱向變形,在試件另一對平行側面中部貼橫向應變片,以量測試件的橫向變形,任何一個方向的應變取2個應變值的平均值,2個方向的應變片長度均為20mm.采用江蘇東華公司生產的DH3816靜態電阻應變儀采集應變數據并記錄保存.

圖1 加載裝置示意圖Fig.1 Diagram of loading equipment

1.3 試驗工況

本文針對PVA纖維摻量、加荷齡期各影響因素進行工況設計,如表2所示.表中F0-28-270表示纖維摻量為0,加荷齡期為28d,持荷時間為270d,其余以此類推.PVA-ECC材料28d力學性能見表3,表中E為彈性模量,μ為泊松比.每組試件應變采集的持荷時間點定為1、3、7、14、28、45、60、90、120、150、180、270d,試驗加載應力水平均為0.4fc.采用電測法以每1h采集1次的頻率對試件變形進行連續采集,最后根據持荷時間節點統計試件的徐變值.

表2 試驗工況

表3 PVA-ECC力學性能

2 徐變性能分析

PVA-ECC的徐變應變可由軸向總變形減去其加荷后的瞬時軸向變形以及相應對比試件的軸向收縮變形得到；徐變系數為單位彈性瞬時應變下的徐變應變,可由徐變應變除以彈性瞬時應變計算而得,如式(1)所示:

φ(t,t0)=εc(t,t0)/ε0

(1)

式中：φ(t,t0)為試件在齡期t0(d)加荷,t(d)時刻的徐變系數;εc(t,t0)為試件的受壓徐變應變,μm/m;ε0為加載至應力σ(MPa)時試件的瞬時軸向應變,其值為加載后數據穩定時所讀軸向受壓應變值，μm/m.

圖2～5為各工況下PVA-ECC材料徐變應變- 持荷時間與徐變系數-持荷時間曲線.圖2～5顯示：徐變發展的整個過程大致經歷了3個階段,在徐變初期,各組試件的徐變值相差較小,曲線幾乎重合,徐變系數呈近似線性增長,且曲線斜率較大,說明加載初期PVA-ECC材料徐變增長迅速,將這一階段稱為徐變快速增長階段；隨著持荷時間的延長,各工況的曲線逐漸分離,且徐變增長速率均開始下降,徐變應變與徐變系數曲線逐漸偏向橫軸,將此階段稱為徐變第2發展階段；之后徐變增長趨于平緩,徐變應變與徐變系數曲線開始收斂,曲線斜率大大降低,將此階段稱為徐變收斂階段.總結徐變隨持荷時間的變化特征,可將之概況為：前期快,后期慢,持荷約60d時徐變的大部分基本完成.將PVA-ECC材料與混凝土的徐變-時間關系進行比較,發現混凝土的徐變終值普遍較小,且其徐變系數-時間關系曲線普遍具有第1階段較短且曲線斜率較小,第2階段曲線較平緩、持續時間長,第3階段曲線斜率稍大,收斂較慢的特征.這說明，與混凝土相比,PVA-ECC材料早期徐變發展速率較快,徐變發生量較大;中晚期收斂較快,徐變發生量較小[28-34].下文將圍繞以上3個階段,對本試驗各工況下PVA-ECC材料的徐變性能進行討論.

圖2 不同纖維摻量下PVA-ECC徐變應變隨持荷時間變化曲線Fig.2 Variations of creep strain with loading time of PVA-ECC under different fiber contents

圖4 不同加荷齡期下PVA-ECC徐變應變隨持荷時間變化曲線Fig.4 Variations of creep strain with loading time of PVA-ECC under different age of loading

圖5 不同加荷齡期下PVA-ECC徐變系數隨持荷時間變化曲線Fig.5 Variations of creep coefficient with loading time of PVA-ECC under different age of loading

2.1 PVA纖維摻量的影響

由圖2、3可見：PVA-ECC的徐變應變和徐變系數隨持荷時間變化曲線的走勢及發展規律基本一致,在纖維摻量范圍內(0%～2.0%),PVA纖維降低了基材抵抗徐變的能力,使試件的徐變增加;纖維摻量越高,材料的徐變越大,纖維摻量為1.0%、1.5%、2.0%的試件在持荷時間為60d時的徐變應變和徐變系數分別是纖維摻量為0%的1.13、1.44倍，1.42、1.09倍，1.56、1.55倍；各組試件在60d時的大部分徐變已發生,纖維摻量為0%、1.0%、1.5%、2.0%的試件在60d時的徐變系數是270d的82%、80%、93%、91%,且纖維摻量越大,60d內發生的徐變占總量的比例越大；隨著持荷時間的進一步延長,60d后徐變增長速度大大降低,曲線趨于平緩,270d 時纖維摻量為1.0%、1.5%、2.0%的試件的徐變應變和徐變系數分別是纖維摻量為0%的1.15、1.27倍，1.29、1.12倍，1.38、1.40倍.由圖2、3還可見：各組試件在第1階段的徐變速率相差極小,曲線幾乎重合,但從第2階段開始,摻纖維試件的徐變增長速率明顯高于基材的徐變增長速率,且纖維摻量越高,試件的徐變增長速度越快.產生這一現象的原因是PVA纖維加入水泥基后,水泥基材與纖維2種材料的界面難以緊密結合,在水泥結硬過程中產生初始微裂縫;加之PVA纖維摻量較大時,纖維容易結團、難以分散均勻,使得材料內部出現較多原始缺陷,降低了材料的密實性,在荷載作用下材料的變形增加.同時,初始微裂縫和缺陷在加荷初期發展不充分,故4組試件在第1階段的變形差距甚微;但隨著荷載的增加,初始微裂縫和缺陷的發展越來越充分,且PVA纖維摻量越大,微裂縫和缺陷越多,材料的變形速率也越大,故曲線在第2階段出現分離.另外,纖維摻量在1.5%和2.0%時試件的徐變始終相差較小,2種纖維摻量下的2條曲線基本重合,且與F1.0-28-270試件的曲線相差較大,說明纖維摻量較高時,纖維摻量變化對試件徐變性能的影響程度變化不大,且結合材料基本力學性能的研究成果[35],說明PVA纖維摻量達到2.0%以后,再提高纖維摻量,PVA-ECC的各項性能均有所下降,且經濟性降低,故在PVA-ECC的實際工程應用中,纖維摻量不宜過大.

2.2 加荷齡期的影響

由圖4、5可以看出,在加荷齡期范圍內(14～180d),在同一持荷時間下徐變應變隨加荷齡期的推遲而減小,即加荷齡期越早,同一持荷時間內發生的徐變越大,此特征與混凝土材料的徐變特性相似.同時,180d加荷齡期時進行加載的試件,徐變系數曲線較徐變應變曲線斜率更大,而其他加荷齡期的試件2類曲線斜率相近,說明隨加荷齡期的推遲,材料的瞬時彈性變形減小.這是因為加荷齡期較早的試件材料成分中水泥水化反應程度不充分,彈性模量偏低,加載后短期內產生較大變形,使瞬時彈性變形量增加;加荷齡期較晚的試件在加載時基材中水泥的水化反應相對進行得較充分,更多的水泥膠凝體向結晶體轉化,基材的彈性模量提高,材料抵抗變形的能力較高,加載后瞬時彈性變形量減小,故同一持荷時間下材料徐變系數提高.另外,與纖維組不同的是,本組試驗中徐變應變曲線與徐變系數曲線從加荷初期便有一定分離,說明在加荷初期,加荷齡期對試件徐變的影響程度大于纖維摻量的影響.

以28d加荷齡期為對照組,14、90、180d加荷齡期各試件與28d加荷齡期試件的徐變比例關系,如圖6所示.

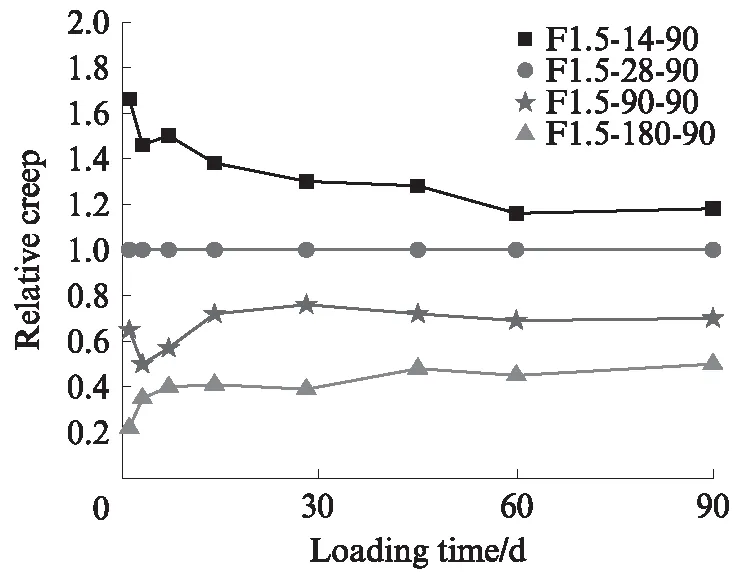
圖6 不同加荷齡期下PVA-ECC相對徐變隨持荷時間變化曲線Fig.6 Variations of relative creep with age of loading of PVA-ECC under different age of loading

通過圖6可知,在90d持荷時間內,不同加荷齡期下的徐變相對28d加荷齡期的徐變比值并不是一定值,加荷齡期越早的試件,加荷初期徐變相對比值越大,說明在加載初期徐變增長速度越快;60d 后徐變增長速度基本趨于一致,相對值穩定在某一定值左右,穩定后14、90、180d加荷齡期與28d 加荷齡期的相對徐變比值約為1.2、0.7和0.4.

3 PVA-ECC徐變的估算

為了能夠獲得普遍適用的徐變計算方法,研究人員提出了較多徐變估算模型.目前國際上對混凝土徐變性能的研究較為成熟,常用的混凝土徐變計算模型有ACI 209R-92模型[36]、CEB-FIP90模型[37]、B3模型[38]和GL2000模型[39].JTG D62—2004《公路鋼筋混凝土與預應力橋涵設計規范》,借鑒了CEB-FIP90模型方法來計算混凝土的徐變系數.而關于PVA-ECC徐變計算模型的研究較少,尚未形成成熟的計算理論.因此本文擬在試驗研究的基礎上,以徐變系數為指標,總結PVA-ECC的徐變發展規律,在已有混凝土徐變計算模型的基礎上，通過與本試驗數據進行對比,對現有的徐變計算模型進行修正與改進,從而得到更符合PVA-ECC的徐變估算模型.下面將著重針對使用較多的ACI 209R-92和CEB-FIP902種模型與本試驗結果進行對比分析.

ACI 209R-92模型可由式(2)表示：

(2)

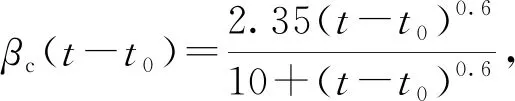
可以看出徐變系數由持荷時間參數βc(t-t0)與徐變修正系數γcr這2部分組成,其中γcr考慮了加荷齡期、環境相對濕度、混凝土構件平均厚度、混凝土稠度、骨料含量及混凝土中所含空氣體積等因素的影響[38].

CEB-FIP90模型可由式(3)～(5)表示：

φ(t,t0)=φ0βc(t-t0)

(3)

φ0=φRHβ(fcm)β(t0)

(4)

(5)

式中：φ0為各義徐變系數；β(fcm)為混凝土強度修正系數；β(t0)為加載齡期修正系數.

可以看出徐變系數由βc(t-t0)和φ0這2部分組成,其中名義徐變系數φ0考慮了加荷齡期、環境相對濕度、混凝土強度、混凝土構件體表比等因素的影響[37].

通過式(2)～(5)可以看出,ACI 209R-92和CEB-FIP90這2種模型都是由持荷時間參數乘以各因素對徐變的影響系數.本文在建立PVA-ECC徐變估算模型時,參考已有混凝土材料徐變計算模型的建立方法,擬采取如下路線進行研究：先排除其他因素對徐變的影響,只考慮持荷時間的影響,得出持荷時間參數βc(t-t0),在此基礎上再考慮各相關因素的影響,乘以各因素的徐變影響系數,得到各工況下PVA-ECC的徐變估算模型.

由試驗結果可知,PVA-ECC材料的徐變前期發展較快,后期發展速度逐步減小，最后趨于收斂,經歷了明顯的3個發展階段.為了更好地反映PVA-ECC材料徐變隨持荷時間的變化特點,在確定徐變估算模型時,本文擬將徐變隨時間發展的函數以分段函數的形式表示.通過對本文試驗數據進行擬合,排除其他因素的影響,得到了PVA-ECC材料的持荷時間參數表達式(模型Ⅰ),如式(6)所示：

(6)

計算在持荷時間為5～14d及45～60d之間的徐變時采用線性內插法.

另外,將式(6)確定的曲線與ACI209R-92和CEB-FIP90模型的持荷時間參數曲線繪于圖7.由圖7可見,在持荷約45d之前時,由式(6)確定的模型曲線與ACI209R-92模型曲線非常接近,但在后期,ACI209R-92模型曲線收斂較慢,二者相差較大;在持荷約60d之后,由式(6)確定的模型曲線與CEB-FIP90模型曲線雖數值相差較大,但斜率非常接近,2條曲線幾乎平行.由此,本文提出PVA-ECC材料徐變估算的第2種計算方法：將ACI209R-92和CEB-FIP90模型中各自能較好反映PVA-ECC材料徐變發展趨勢的曲線段進行組合,形成PVA-ECC材料的徐變計算模型(模型Ⅱ),即持荷45d之前采用ACI209R-92模型計算,持荷60d之后采用CEB-FIP90模型計算值加常數項進行計算,經與本試驗數據進行對比分析,建議取常數項為0.60.模型Ⅱ計算式如式(7)所示：

(7)

圖7 各模型下持荷時間參數曲線關系Fig.7 Curve relation of loading time parameter of different models

計算持荷時間為45～60d期間的徐變時采用線性內插法.

將模型Ⅰ、模型Ⅱ確定的持荷時間參數曲線與由本文試驗數據確定的曲線統一繪于圖8.由圖8可知：模型Ⅰ的計算結果在整個徐變發展過程中與試驗結果吻合程度較高;模型Ⅱ在計算前期徐變時與試驗結果吻合較好,計算穩定后的持荷時間參數時計算結果略大于模型Ⅰ,但由于模型Ⅱ前2個階段的徐變函數由1個公式表達,故其計算相對較簡便.

圖8 式(6)、(7)與試驗數據對比關系Fig.8 Comparisons between equation (6), equation (7) and experimental data

在此基礎上進一步考慮纖維摻量與加荷齡期的影響,在式(6)、(7)的基礎上乘以影響系數,得到關于PVA-ECC徐變系數φ(t,t0)的計算式：

φ(t,t0)=kf·kd·βc(t-t0)

(8)

其中，

(9)

kd=1.622-0.012t0+0.00004t02

(10)

式中：kf為PVA纖維體積摻量修正系數;kd為加荷齡期修正系數;Vf為PVA纖維摻量,纖維摻量大于1.5%時按照1.5%取值.

通過式(8)～(10)計算出的PVA-ECC受壓徐變系數計算值與試驗值的比值見表4,除個別點外,計算值與試驗值吻合度較高.通過與試驗數據進行比較,由模型Ⅰ與模型Ⅱ建立的PVA-ECC材料徐變估算公式計算值與試驗值的比值均值為1.09、1.18,方差為0.04、0.07,誤差滿足工程精度要求,且相對于模型Ⅱ,模型Ⅰ具有更高的精度.

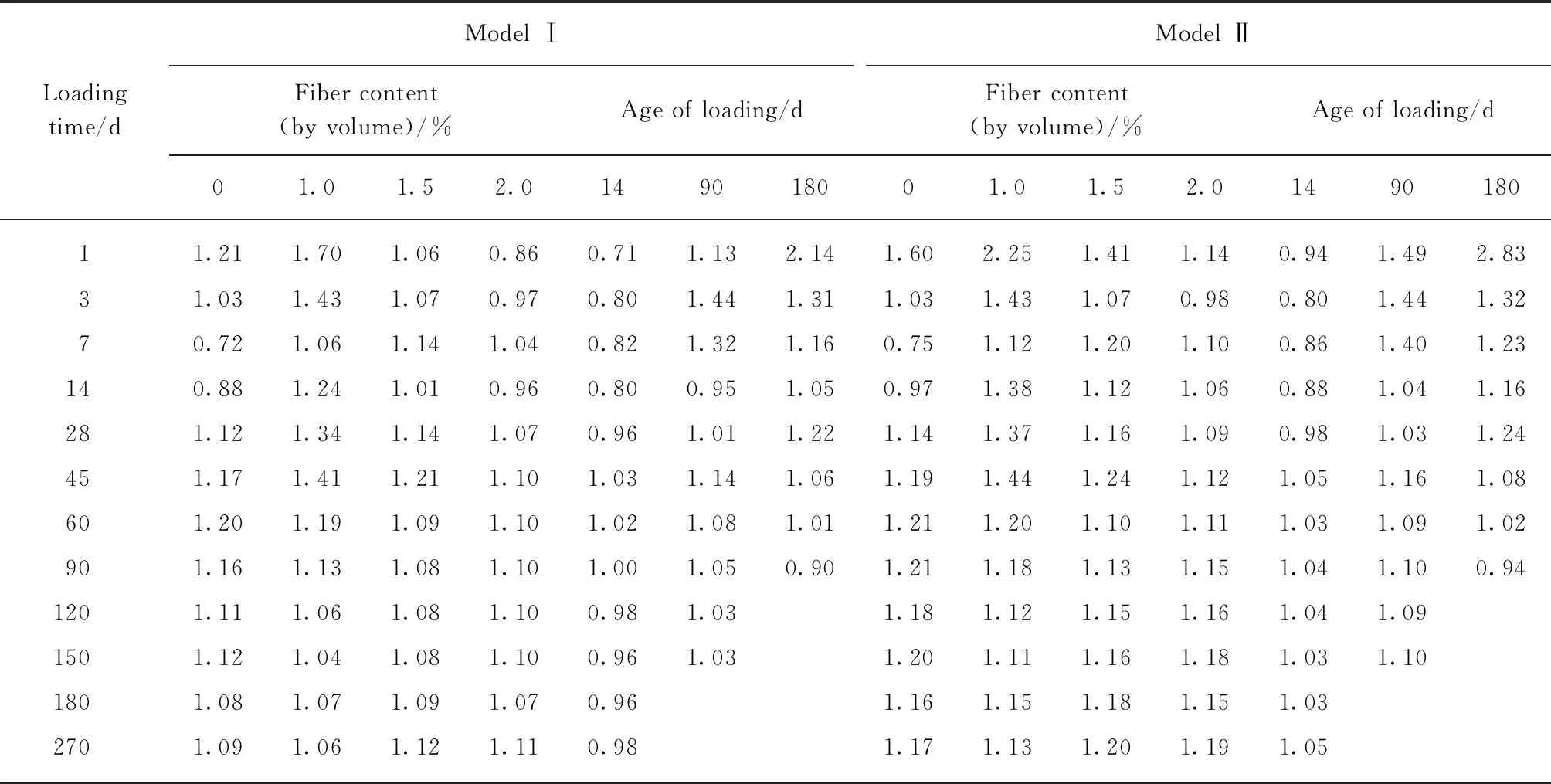
表4 PVA-ECC徐變系數計算值與試驗值的比值

4 結論

(1)與混凝土徐變發展過程類似,PVA-ECC的徐變發展也呈現出前期快、后期慢,最后逐漸趨于穩定的變化規律.

(2)在設計工況條件下,PVA-ECC材料的徐變應變和徐變系數隨纖維摻量的增加而增大,隨加荷齡期的延長而減小.

(3)結合已有的混凝土徐變預測模型和本文試驗結果,提出PVA-ECC材料徐變估算的2種模型,且2種模型的計算值與試驗值均具有較好的吻合度,誤差滿足工程精度要求.模型Ⅰ的計算結果比模型Ⅱ具有更高的精度,但模型Ⅱ的計算過程相對簡便.本文提出的徐變估算模型可為今后PVA-ECC結構構件在長期荷載作用下的徐變計算及變形驗算等提供參考依據.