非粘結柔性立管軸對稱載荷作用下的理論模型分析
張海琛,佟麗莉,王麗君,沈羿充,劉浩
哈爾濱工程大學 航天與建筑工程學院,黑龍江 哈爾濱 150001
海洋立管是指用于連接水面浮體和海床井口的隔水套管系統,是深海生產系統中最復雜的一類設備。非粘結柔性立管是由柔性管發展而來的,是一種多層復合壁管,各層管壁采用不同的材料制成,且在承受外部或內部載荷時,各層管壁相互間能夠發生輕微的滑動,因此具有較低的彎曲剛度。因為柔性立管具有順應性強、便于安裝與回收、設計空間很大等優點,在深海中得到了廣泛的應用。非粘結柔性立管常由多層不同的結構組成[1?2]。柔性立管所處的環境復雜,需要對于柔性管在各種荷載作用下進行分析研究,以保證立管的安全可靠。
針對柔性立管的截面靜力分析,國內外學者展開了大量的研究。Felippe 等[3]和Chung 等[4]利用可以產生軸向變形、彎曲變形和扭轉變形的三維梁單元來模擬管道模型,分析得出了海洋立管靜態下的非線性平行構型方程。Witz 等[5]和Tan等[6]推導出了柔性管在彎曲荷載下的臨界曲率以及螺旋條帶的曲率表達式,以及柔性立管在未滑移階段和完全滑移階段的彎曲剛度。任少飛等[7?8]、陸鈺天[9]和陳耕[10]根據最小勢能原理推導出多層柔性立管的整體剛度矩陣。Yoo 等[11]考慮了柔性立管的非線性特性,使用整體剛度矩陣,計算了柔性立管的抗拉剛度。董磊磊等[12]基于能量法推導出了柔性立管結構分析模型。郭有松等[13]和陳希恰[14]基于靜力平衡、變形協調、本構關系和層間接觸關系,推導出了柔性立管軸對稱響應的理論模型。裴曉梅等[15]推導了柔性立管的整體抗拉剛度和抗扭剛度計算公式。
本文基于最小勢能原理推導出了柔性立管各層的剛度矩陣,并疊加得到整體剛度矩陣。使用罰函數的方法引入層間接觸,并建立接觸的剛度矩陣,加到整體剛度矩陣上得到考慮層間接觸的柔性立管整體剛度矩陣。然后使用該矩陣計算非粘結柔性立管在拉伸、內壓以及扭轉作用下的變形響應。并將結果與有限元軟件計算結果進行對比。
1 理論模型
根據非粘結柔性立管在在軸對稱荷載作用下的力學性能研究,可以將將柔性管分為2 個基本構件:圓柱層和螺旋層。螺旋層包括抗拉鎧裝層、抗壓鎧裝層、骨架層,其主要為金屬材料,為立管提供軸向和徑向剛度。圓柱層包括防磨層、防滲漏層等,主其要材質為聚合物,為立管提供密閉性,減小層間摩擦損傷。各層之間采用非粘結的接觸方式連接。典型非粘結柔性立管結構如圖1 所示。

圖1 典型非粘結柔性立管結構
為了便于推導,本文假設:
1)柔性管具有較大的軸向和徑向剛度,所以各層變形均為小變形;
2)模型中的材料視為線彈性且各向同性;
3)柔性管各層的軸向變換量和繞軸向扭轉角度相同。
1.1 螺旋層剛度矩陣
螺旋條帶在軸對稱荷載作用下可能發生軸向應變、徑向應變以及彎曲和扭轉變形[9]。
1.1.1 螺旋鎧裝層條帶的軸向和徑向應變
抗拉鎧裝層以30°為主的角度纏繞而成,多為矩形截面,如圖2 所示。柔性立管長度為L;螺旋鎧裝層半徑為R;纏繞角度為 α。
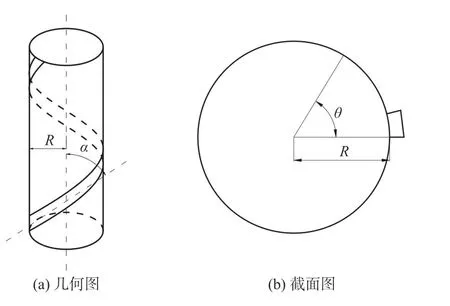
圖2 螺旋鎧裝層
螺旋條帶的軸向應變為[7?10]
式中: μZ為立管螺旋層軸向位移; μR為徑向位移;μθ軸向扭轉角。
螺旋條帶的徑向應變為
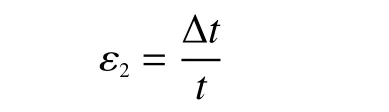
式中: ?t 為螺旋條帶厚度變化; t為螺旋條帶初始厚度。
根據彈性力學,應力應變關系為
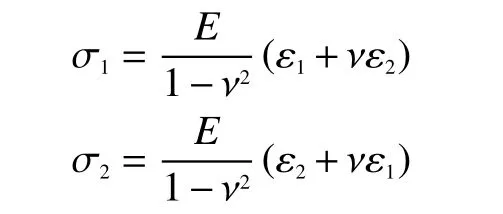
式中: σ1為 螺旋條帶軸向應變; σ2為螺旋條帶徑向應變; E 為螺旋條帶材料彈性模量; ν為螺旋條帶材料泊松比。
螺旋條帶在軸對稱荷載作用下的應變能為
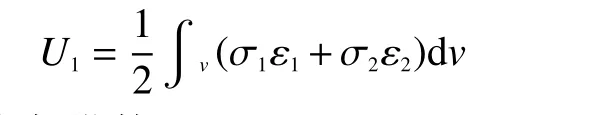
式中 v為螺旋條帶體積。
螺旋層在軸對稱荷載作用下的外力勢能為
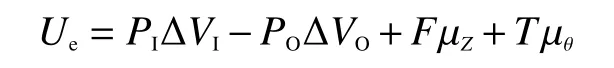
式中: PI為 螺旋層受到的內壓; PO為螺旋層受到的外壓; ?VI為螺旋層內表面體積變化; ?VO為螺旋層外表面體積變化;F 為螺旋層受到的軸向拉力;T 為螺旋層受到的軸向扭矩。
1.1.2 螺旋層條帶的彎曲和扭轉
條帶局部彎曲和扭轉產生的應變能為
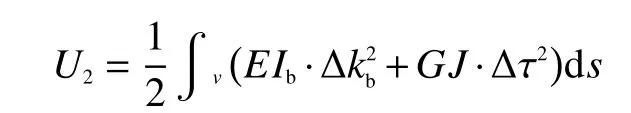
式中: Ib為螺旋條帶截面對副法線向量方向的慣性矩, G為 螺旋條帶的剪切模量, J為螺旋條帶截面的極慣性矩。
螺旋層在軸對稱荷載作用下的總勢能為

1.2 圓柱層剛度矩陣
在小變形范圍內,將聚合物材料視為線彈性且各向同性。對于聚合物圓柱殼采用厚壁理論分析。受力及變形圖如圖3 所示。
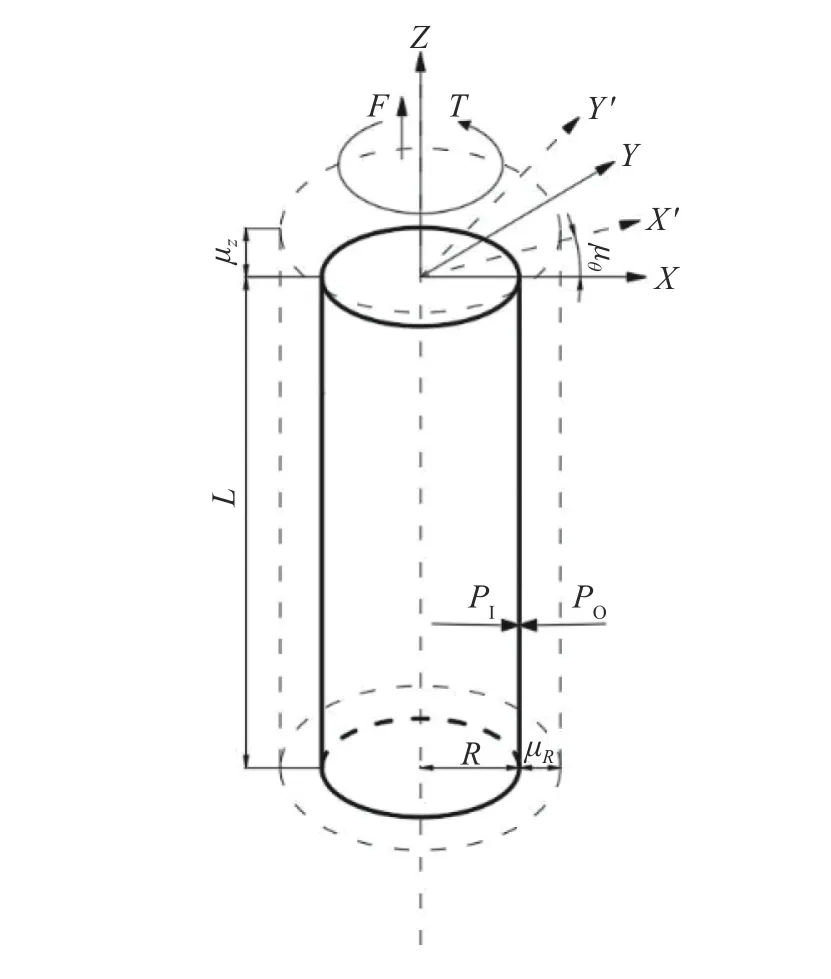
圖3 圓柱層受力及變形
由圖3 可知,圓柱層軸向應力和應變為 σ1、 ε1;徑向應力和應變為 σ2、 ε2;環向應 力和應變為 σ3、ε3; 剪切 應 力和 應 變為 τ12、 γ12;徑 向位 移為 μR。其中 ε1、 ε2、 ε3、 γ12為
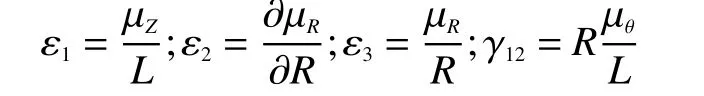
彈性階段,平面應變問題應變和應力分量之間的關系可表示為
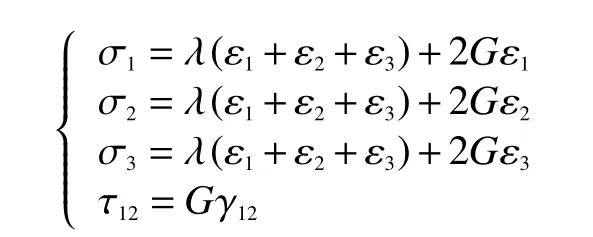
圓柱層的外力勢能計算公式和螺旋層相同,應變能可表示為

1.3 接觸附加矩陣
非粘結柔性立管在受力情況下,各層之間可能發生接觸或者分離,因此對其分析的過程中需要考慮層間接觸的影響。
在柔性立管中,根據幾何連續條件可得各相鄰層之間的空間幾何關系[7?10]:
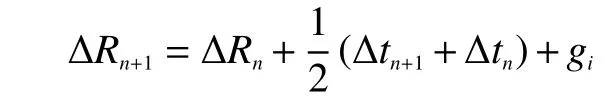
文獻[9]將法向接觸條件引入柔性管的整體剛度矩陣。由約束變分原理可知,對于有附加條件的問題可以使用罰函數法將附加條件引入泛函,構造一個新的泛函。附加泛函為
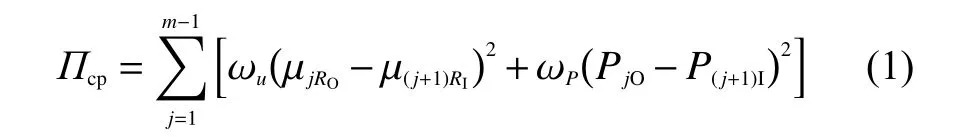
式中: j為柔性管的層數(一共為m 層); ωju和 ωjP為第 j層的罰參數; μjRo為第 j層外表面的徑向位移;μ(j+1)RI為第 j+1層 內表面的徑向位移; PjO為 第 j層外表面的外壓; P(j+1)I為第 j+1層內表面的內壓。在未接觸時, μjRO=μ(j+1)RI=0。
采用罰函數法將法向接觸條件引入泛函,可表示為
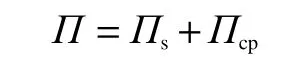
為方便計算,直接對式(1)取變分,并使其等于零。可以得到柔性立管各層之間的接觸矩陣。矩陣階數與整體剛度矩陣相同,表示為 kcp,與整體剛度矩陣階數相同。
以常見8 層柔性立管結構為例,其中骨架層和抗壓鎧裝層簡化為各向異性的殼,則剛度矩陣為18 階,接觸矩陣也為18 階。

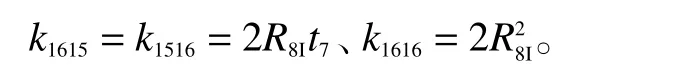
1.4 建立剛度矩陣
柔性立管各層結構的軸向變形和扭轉變形是相等的,因此m 層柔性立管共有2+2m 個自由度:
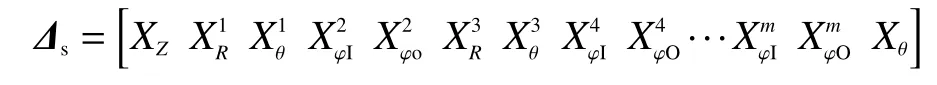
式中:X 表示自由度,上標表示層號,下標表示自由度類型。
整體剛度矩陣也應為2+2m 階。將各層的剛度矩陣以自由度為依據,組合成自由狀態下的整體剛度矩陣k。最終考慮層間接觸的剛度矩陣為
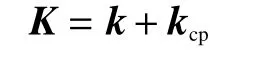

式中 FZ、 PI、 PO、 N分別為軸向力、內壓、外壓和扭矩。
2 有限元模型
2.1 立管基本參數
本文根據de Sousa[16]已發表的關于非粘結柔性立管的實驗論文,在表1、2 給出了2.5 英寸柔性管各層幾何參數和材料參數。

表1 實驗柔性立管幾何參數
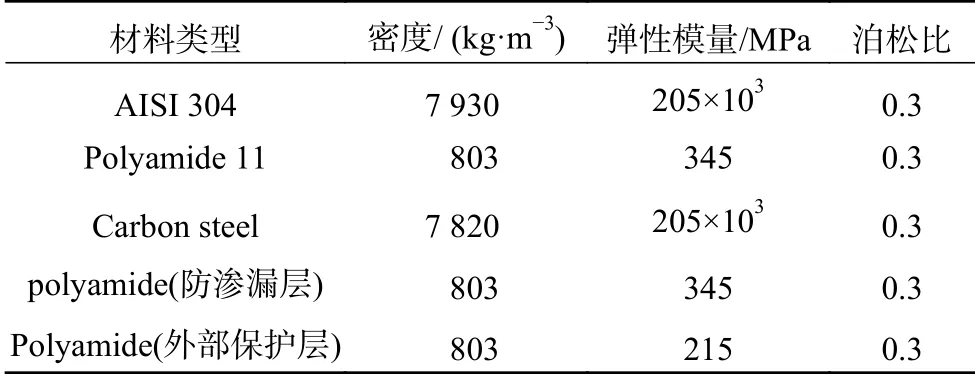
表2 材料參數
2.2 模型與網格
使用三維建模軟件建立8 層柔性立管三維模型,導入ABAQUS 對其進行網格劃分,使用C3D8R單元,如圖4 所示。層間接觸采用庫倫摩擦來模擬,摩擦系數取0.1。

圖4 柔性立管有限元模型
2.3 分析步和邊界條件
先定義一個很小的荷載的分析步,讓接觸關系平穩地建立起來,然后在下一個分析步中再施加真實的荷載。這樣雖然分析步數目增多,但減小了收斂的困難,計算時間反而縮短[17]。采用ABAQUS/Explicit 準靜態方法進行計算,采用Smoot step 的加載方式[18]。
本文先在端部截面中心設置參考點,然后對截面上所有節點的自由度與參考點進行運動學耦合。在一端參考點施加固定約束,另一端參考點施加拉伸或扭轉荷載[18]。
3 計算結果分析
3.1 罰參數計算
罰函數法在接觸問題中可以不增加問題的自由度,所以應用較為廣泛。但是求解的精度與罰參數相關。圖5 為在純軸向拉伸作用下,軸向變形與罰參數w 之間的關系曲線。
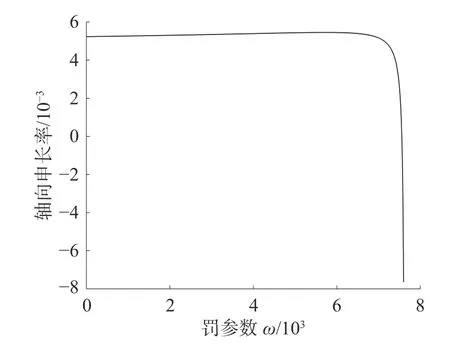
圖5 罰參數對結果的影響
將結果與文獻[16]中的實驗結果對比,可以發現,隨著罰參數的增大,計算結果越來越準確;但是當罰參數大于7 000 后,軸向伸長率出現了大幅度的變化,這就是由于罰參數過大造成了方程的病態。因此本文的罰參數的選擇在6 000~7 000。
3.2 拉伸工況
使用第1 節中的整體剛度矩陣Kc計算軸向拉力作用下立管的受力情況。700 kN 作用下各層的徑向變形值可從位移理論方法計算所得的變形向量中得到,結果見表3。對比各層內外徑的徑向變形值,如第5 層外徑變化較第6 層內徑變化大,可以推斷出層間發生了分離。從表中可以看出:第4 和第5 層、第6 和第7 層是相互接觸的;但是第5 和第6 層、第7 和第8 層發生了分離。
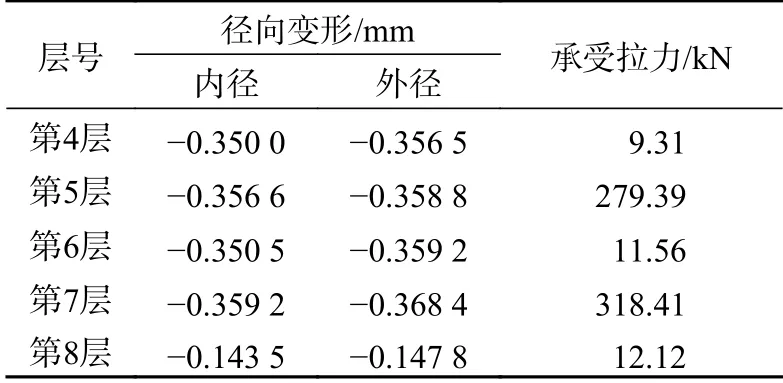
表3 700 kN 軸向拉力作用下各層受力情況
在純拉力作用下,柔性立管的伸長率與有限元模型計算結果如圖6 所示。計算結果與文獻[16]的實驗結果相比,誤差在10%以內,且數值模型誤差更小。
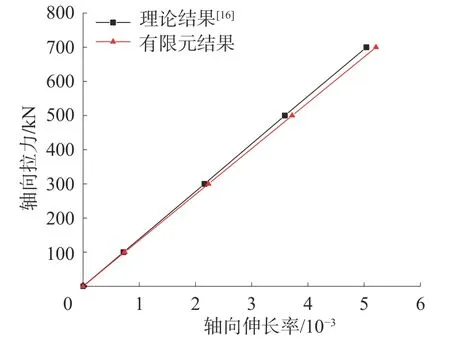
圖6 軸向拉力與軸向伸長率關系曲線
由圖6 結合文獻[16]可以看出,立管的軸向變形隨著軸向力的增大線性增加,比較理論計算結果與數值計算結果,二者誤差為5%。將位移向量中的值代入各層的計算方程中,可以得到每一層所承受的軸向拉力值。表3 中給出了700 kN軸向拉力作用下的各層結構所承受的軸向拉力值。從中可以看出,第5、6 層承擔了柔性立管軸向拉力的84%。由此可得非粘結柔性立管的軸線剛度主要由抗拉鎧裝層提供。在拉伸工況下,應力較其他層大,圖7 為純拉伸作用下有限元計算方法得到的抗拉鎧裝層應力圖。
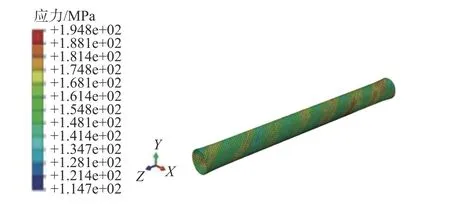
圖7 700 kN 軸向拉力作用下螺旋鎧裝層應力分布
3.3 扭轉工況
取內抗拉鎧裝層纏繞方向為順時針方向。根據各層徑向變形值,同樣可以得到各層之間的接觸關系。表4 為柔性立管在7 kN·m 的扭矩作用下,第4~8 層的受扭矩情況。從表中可以看出,在立管發生扭轉時,抗拉鎧裝層承受扭矩的86%。
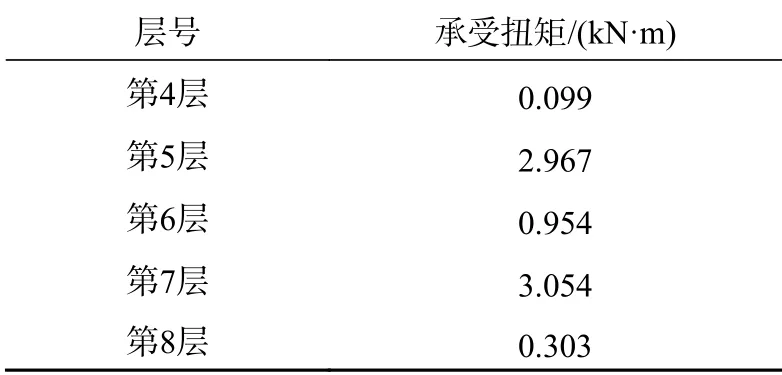
表4 7 kN·m 扭矩作用下各層承受扭矩情況
扭矩作用下的理論計算結果和有限元計算結果對比如圖8 所示。
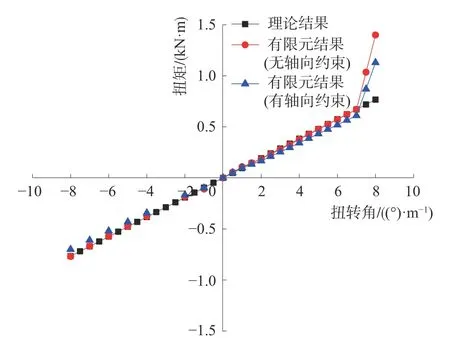
圖8 扭矩與扭轉角關系曲線
從圖中可以看出,柔性立管的扭轉角隨著扭矩的增大而線性增長。理論計算結果與無軸向約束的立管的數值模擬結果相差1.5%。而由于順時針扭矩產生的整體剛度減小現象,理論方法無法表現出來。
4 結論
本文依據柔性立管各層的結構特性,建立了用于計算軸對稱荷載作用下柔性立管各層的剛度矩陣,并將其組裝得到自由狀態下的剛度矩陣。通過罰函數的方法將層間法向接觸引入立管整體矩陣,利用式(1)推導出接觸矩陣,并加到自由狀態下的剛度矩陣上,得到非粘結柔性立管的整體剛度矩陣。本文算例中計算了典型8 層結構的柔性立管,并建立了三維有限元模型。討論了接觸矩陣中罰參數的取值,并對比了柔性立管在軸向拉力和扭矩作用下變形的理論解和數值模擬值。最終得出結論如下:
1) 8 層柔性立管結構,罰參數可以在6 000~7 000 取值。層間接觸矩陣中的罰參數取值對計算結果影響較大,在不同結構參數下需要先確定罰參數的取值。
2)參考文獻中的試驗結果,并將本文中的理論模型與數值模型計算結果與之對比,發現誤差在10%以內,證明了本文的剛度矩陣計算方法可以在設計前期使用,以便節省時間,但是在具體設計階段,仍需要實驗進行驗證。

