隱形矯治方案中的牙齒運動路徑規劃方法研究

李占利，劉童鑫，李洪安，孫志浩

隱形矯治方案中的牙齒運動路徑規劃方法研究

李占利，劉童鑫，李洪安，孫志浩

(西安科技大學計算機科學與技術學院，陜西 西安 710054)

針對隱形矯治方案制定過程中傳統牙齒運動路徑規劃方法準確度及效率低下問題，根據牙頜評價參數提出新的目標函數，再以傳統的人工蜂群算法(ABC)為基礎，通過外部存儲存放Pareto解集，然后以改進的Harmonic距離對Pareto解集進行更新，從而提高種群的多樣性。隨后通過Slerp球面線性插值以及線性插值獲取牙齒運動路徑初始值，與人工蜂群算法中的初始食物源生成方式相結合，生成更好的食物源。通過改進后的人工蜂群算法采用優先級方案對新目標函數進行優化，得到牙齒的無碰撞運動路徑。通過驗證本文方法的矯治方案效果，并與傳統目標函數進行比較，結果表明目標函數可以生成更符合臨床治療要求的矯治方案，改進ABC算法相比基本ABC能夠獲得更優的路徑，縮短了矯治階段數，具有實用價值。

隱形矯治；路徑規劃；人工蜂群算法；多目標優化

無托槽隱形矯治技術作為一種新型口腔正畸技術，相對于傳統矯治技術有著便于拆卸、透明美觀、干凈衛生的優勢，在正畸治療中很受歡迎[1]。隨著計算機輔助設計與口腔正畸學的不斷發展與融合，使得隱形矯治計算機輔助系統成為研究熱點[2]。在隱形矯治過程中，由牙醫根據病人的畸形類型以及病人的訴求進行矯治方案的規劃，即牙齒運動路徑上關鍵中間位置的確定，然后將方案通過隱形矯治系統可視化，并將各階段方案的變化展示給病人，病人同意后進行各階段矯治器母模的加工[3]。

目前，牙齒運動路徑規劃局限于交互式手動排列，操作如下：

(1) 選定合適的牙弓曲線模型；

(2) 記錄牙齒的初始坐標與理想位置坐標；

(3) 依照牙弓曲線，采用虛擬正畸軟件對牙齒進行手動平移、旋轉等操作，設計牙齒的運動路徑。

交互式手動規劃效率低、誤差大、精度不夠，而且會因為視覺誤差影響最終結果。

針對上述問題，部分學者做出了自動化牙齒路徑規劃方法。王先澤等[4]提出基于粒子群(particle swarm optimization，PSO)的自動化規劃方法，其針對手動交互效率不高的缺點，以每顆牙齒選取的特征點到標準牙弓曲線的距離和作為目標函數，以牙齒間的間距作為約束條件，實現了對牙齒路徑的自動規劃，但未考慮牙齒旋轉角度的因素；MOTOHASHI[5]以牙弓線牽引的方式實現了牙齒運動路徑規劃，但未考慮如病人牙列擁擠，可導致牙齒間發生碰撞，實際效果不好的特殊情況；楊光[6]以牙齒移動量及旋轉量為目標函數，通過約束條件，以A*算法進行優化求解牙齒運動中間位置，從而獲取牙齒運動路徑，目標函數中的旋轉量只考慮了旋轉角，未考慮軸傾角及轉矩角；張筱[7]提出單顆牙齒分別規劃的方法，并在牙齒移動規劃過程中加入了碰撞檢測，得到牙齒正畸路徑規劃方法的可視化結果，因牙齒運動是多個牙齒同時移動的，可能會發生碰撞。

牙齒運動是一個在三維空間中，涉及到平移、旋轉等多方面運動狀態的過程。在前人的研究中，由于運動過程中目標函數的不足或是算法性能原因，使得規劃效果并不理想。針對傳統交互式牙齒路徑規劃方式以及目前自動化牙齒路徑規劃方式中的缺陷，根據牙頜測量方法標準，提出更全面的參數目標函數，然后以傳統人工蜂群算法為基礎，通過自適應罰函數處理約束問題，以外部存儲的方式存放Pareto解集，通過改進的Harmonic距離對解集進行更新，提高種群分布性。然后通過插值方法獲取牙齒運動理想路徑，結合人工蜂群算法的初始化過程，生成更好的初始食物源。最后以改進后的人工蜂群算法對牙齒依照優先級策略進行路徑規劃。最后通過實驗對本文改進方法進行驗證及對比，結果表明，該方法規劃出的路徑更加精準，牙齒運動代價更小。

1 數學模型

1.1 牙齒矯治方案定義

在牙齒矯治之前，醫生會根據患者的錯頜類型、年齡以及個人訴求為患者規劃正畸方案，然后將整個矯治過程用計算機動畫進行模擬，記錄牙齒關鍵中間位置，也就是矯治過程中牙齒運動的路徑點，并將其展示給患者，記錄得到的關鍵中間位置，結合3D打印技術，制作每一階段的隱形矯治器。所以，在牙齒矯治方案中，關鍵的技術點在于規劃牙齒運動的路徑。對牙齒運動路徑規劃方案的評價是一個綜合了數學計算、計算機技術等多個方面的復合分析過程，其本質就是綜合了牙科標準和生理限制對牙齒運動路徑的準確性、時效性、經濟性以及美觀程度等方面進行評價。

1.2 矯治方案評價參數

1.2.1 Spee曲線和牙列擁擠度

Spee曲線[8](下頜牙列的縱頜曲線)是連接下頜切牙的切緣、尖牙的牙尖、前磨牙的頰尖以及磨牙的近遠中頰尖的連線，可反映下頜平整度。文獻[9]指出，越是理想的牙頜形態，其Spee曲線就越平滑。在正畸學中，牙列擁擠度能直接決定是否需要進行拔牙或擴弓治療，如果患者牙列過于擁擠，則更易碰撞，與矯治器附件互相作用，導致牙齒無法到達理想位置，使矯治方案無法準確實施，所以牙列擁擠度是矯治方案效果的評價依據。牙列擁擠度與Spee曲線有密切的關系，Spee曲線越平滑，牙列的擁擠度會變大，引起如牙齒向唇側突出的問題。一般情況下，每平整1 mm的Spee曲線，需要縮小1 mm的牙弓間隙。所以Spee曲線深度和牙列擁擠度應該控制在一個平衡的范圍內，過度松散及擁擠均會給病人帶來不適。Spee曲線及咬合面關系如圖1所示。

圖1 Spee曲線

1.2.2 牙弓對稱性

牙弓對稱性[10]主要包含：①上下頜關于咬合面的對稱性；②同一牙列兩側牙齒關于牙弓中軸線的對稱性。牙弓對稱性如圖2所示。

圖2 牙弓對稱性

將上頜牙弓的中軸線投影到咬合面上，該投影與下頜中軸線方向向量之間的夾角越小則表明上下牙弓越對稱。

兩側牙齒之間的對稱性則分別在各自所在牙弓進行，以上頜為例，將磨牙的近中舌側牙尖點、前磨牙的舌側牙尖點以及尖牙的牙尖點投影到咬合平面，向上頜牙弓中軸線作垂線，線段長度代表牙齒到中軸線的距離，通過測量兩側牙齒到中軸線的距離，其差值越小則越對稱。

1.3 正畸參數計算

1.3.1 Spee曲線深度

口腔學將牙尖點中最低的點到第二磨牙遠中頰尖與中切牙最高點所構成的直線距離，稱為Spee曲線深度，即

其中，為咬合面的高度；為牙尖點高度，取最小值。為了使Spee曲線盡量平滑，式(1)需取極小值。

1.3.2 牙列擁擠度

牙列擁擠度，是指牙弓原本應有的長度與現有長度之差。牙弓應有長度代表所有牙齒寬度之和。牙弓現有長度是指當前牙弓線長度。

當前牙弓線長度可以用四次二維曲線來表示，將牙齒特征點投影到咬合面，然后用最小二乘法擬合出該曲線，即

則可得到牙弓線現有長度為

牙列擁擠度為

其中，W為第顆牙齒的寬度。

1.3.3 牙弓對稱度

分析上下頜兩側同名牙齒之間的對稱度，將兩側牙尖到中軸線的距離差值的絕對值進行累加，再除以牙齒的對數，即可求出牙弓對稱度[11]，即

其中，D為觀察者左側的牙齒到中軸線的距離；D為觀察者右側的牙齒到中軸線的距離；為牙齒數量，/2則是牙齒的總對數；當越小，則兩側牙齒的對稱度越高。

1.3.4 牙齒移動量與旋轉量

假設分割后的牙齒數量為，則顆牙齒中的每一顆從初始位姿到最終位姿都會構成一系列的離散點，這一系列的離散點即為路徑點。其中每個路徑點就是每一矯治階段中該牙齒所在的位置，路徑點的總數需要在路徑規劃前確定，在每一階段中，牙齒的運動狀態又可分為平移與旋轉。

最終顆牙齒的正畸方案為

設第顆牙齒的運動函數為

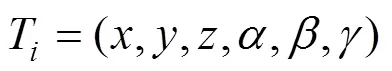
其中，，，分別為第顆牙齒在局部坐標系中沿3個方向的移動量；，，分別為牙齒的轉矩角、軸傾角、旋轉角。

最終的目標轉化為對下列的問題求解

其中

其中，d為牙齒在第階段的移動量，即

且，為牙齒在第階段的旋轉量。

1.4 目標函數

經過上述評價參數的建立，得到需要最優化的目標函數集合

1.5 約束條件

1.5.1 碰撞檢測

在牙齒移動過程中，為避免同步移動時的干涉問題，故要在規劃過程中對牙齒進行碰撞檢測，即

其中，c為當前第顆牙齒是否在第階段與相鄰牙齒發生碰撞，默認值為0，發生碰撞則為1；為判斷當前路徑是否發生碰撞，當=1為發生碰撞。

1.5.2 移動量和旋轉量

在矯治過程中，牙齒一次平移量與旋轉量不能過大，有

其中，0取0.5 mm；0取3°。

1.5.3 牙齒間距

牙齒在沿正畸路徑移動時需要考慮到牙齒間距，相鄰牙齒的間距不大于0.5 mm，即

其中，d()為第與第+1顆牙間距。

由上文可知，牙齒運動路徑規劃問題的最終求解為

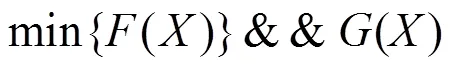
其中，()為需要最優化的目標函數集合；()為約束函數集合，式(18)要在滿足約束條件的情況下取得目標函數最小值，因此牙齒運動路徑規劃問題實際上是一個帶約束條件的多目標優化問題。

2 基于人工蜂群算法的約束多目標優化

2.1 基本人工蜂群算法

為了解決全局優化問題，KARABOGA[12]提出了人工蜂群(artificial bee colony，ABC)算法。其是根據蜜蜂采蜜行為提出的一種優化方法，可通過直接比較參數的優劣來實現局部尋優，快速收斂，從而迅速找出全局最優值。

ABC算法將蜂種按分工分為雇傭蜂、觀察蜂和偵察蜂，其中雇傭蜂與食物源對應，一個食物源為一個可能的解決方案，花蜜量代表該解決方案對應的目標函數值。觀察蜂以適應度選擇食物源，經過一定數量的選擇(控制參數)，若食物源得不到更新，則棄之，該雇傭蜂變為偵查蜂，再次搜尋食物源，且此偵查蜂又變回雇傭蜂。許多研究者利用人工蜂群算法易用、高效的特點，將其應用于路徑規劃領域。初始人工蜂群算法的步驟如下：

步驟1.初始化。在初始化階段，假設蜂群規模為，則偵察蜂與觀察蜂的數量均為=/2，首先由偵察蜂隨機生成個食物源，即

其中，x為第個食物源的位置，=1,2,...,，=1,2,...,，為優化問題的維數；ub和lb分別為該食物源第維變量可取的上界和下界。

對每個初始食物源計算適應度，并記錄其適應度值設置為，并將最優食物源記為best，初始化當前食物源開采次數變量()=0，適應度為

步驟2.循環以下4步，直至到達終止條件。

(1) 雇傭蜂搜索。雇傭蜂在當前食物源周圍搜索新的食物源，搜索策略為

其中，x為當前食物源的一個相鄰食物源，通過計算新食物源的適應度并與當前食物源適應度進行比較，選擇適應度較高的食物源，即

若成功更新了當前食物源，則將新食物源()置零，否則()自增一次。

(2) 觀察蜂評價。觀察蜂可根據食物源的適應度計算食物源的跟隨概率p

獲得p后，利用輪盤賭機制決定當前食物源是否更新，若更新則按照雇傭蜂策略局部搜索新食物源。

(3) 偵察蜂搜索。對當前食物源的()進行判斷，當超過搜索次數上限時，則按照式(19)全局搜索新的食物源來代替當前的枯竭食物源。

(4) 記錄最好食物源。通過變量記錄當前蜂群中的最大適應度，并與進行比較，且更新

若最好食物源得到更新，則同步更新種群中的最好食物源記錄best。

步驟3.當迭代次數超過，輸出最終解best。

2.2 算法優化

2.2.1 動態罰函數處理約束問題

KARABOGA和BASTURK[13]通過Deb準則解決了約束問題，但也破壞了種群的多樣性，不利于算法收斂。本文提出使用罰函數將約束優化問題轉化為無約束優化問題，根據牙齒運動約束量，罰函數為

其中，g()為小于號約束條件；h()為等號約束條件；H(g())和H(h())為指示函數，分別為

其中，為懲罰系數，其值通過自適應方法來選取，即

2.2.2 改進的Harmonic距離排序構造Pareto解集

本文通過外部存儲來存放Pareto解集，其計算及更新方式基于擁擠距離排序方法進行優化。擁擠距離排序方法在NSGA-Ⅱ[14]算法中被提出，用于描述某一最優解周圍分布其他解的密度，便于排除冗余度大的解，保留其他具有多樣性的解，從而確保全局尋優能力。文獻[15]指出，與擁擠距離相比，Harmonic距離用來反映個體間的擁擠程度效果更好，其表達式為

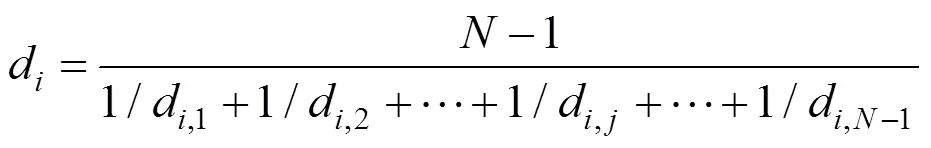
其中，為種群規模；d,j為個體x與x在目標空間上的歐氏距離。

擁擠密度改進方法一方面減少了計算量，提高了算法效率，另一方面計算擁擠距離時也考慮到了距離較遠的個體，不影響解集的分布性，還考慮了當前精英個體的影響，降低了較差個體帶來的影響。因此，改進的Harmonic擁擠距離計算在提高效率的同時減少了不良影響，能準確反映個體的分布情況，兼顧了種群多樣性。

綜上，本文Pareto解集更新方式為：設外部存儲Pareto解集的容量為。

步驟1. 在每個優化目標上，按目標函數值對當前所有個體進行升序排列，選擇Pareto等級較優的個體放入中，若容量超出限制，則跳至步驟2，否則繼續計算直至遍歷結束；

步驟2.利用式(29)計算目前解集中最劣Pareto等級個體的擁擠距離并降序排列，刪除擁擠距離較小的個體，如果有2個或更多最小解，隨機移除一個。

3 牙齒運動路徑規劃

3.1 結合牙齒運動路徑規劃的初始食物源生成

在人工蜂群算法中，初始化階段是由偵察蜂全局生成初始食物源。對于牙齒運動路徑規劃而言，最優路徑實際上是直接從起始位姿平移旋轉到目標位姿，是理想無碰撞情況下的路徑，而實際正畸過程中，會出現牙齒間的碰撞、約束及運動量約束等問題，因此需要在理想路徑的基礎上優化出無碰撞、滿足約束的路徑。基于此，需首先獲取理想狀態下的牙齒路徑，并以此作為初始食物源，然后結合人工蜂群算法對路徑進行優化。

3.1.1 旋轉量插值

圖3 線性插值

圖4 球面插值

在牙齒運動路徑規劃過程中，由于正畸力不便于控制，所以假設牙齒的角速度恒定，本文采用球面線性插值(spherical linear interpolation，Slerp) 來進行牙齒旋轉量插值，即

3.1.2 平移量線性插值

在歐氏空間中，任意2點間的最短距離為 2點的直線距離，因為牙齒的平移量只需根據上文中移動量約束進行均勻插值，可分為若干正畸階段，如圖5所示，其中0i為牙齒初始位置；C為牙齒目標位置。

圖5 平移量插值

3.1.3 初始食物源生成

在獲取了牙齒旋轉量及平移量插值后，也就獲得了牙齒在理想情況下的運動路徑，圖6為側切牙插值結果。此時結合人工蜂群算法中的偵察蜂搜索策略，以插值路徑作為初始值，生成初始食物源，步驟如下：

步驟1.設定牙齒平移步長約束0和旋轉步長限制0；

步驟2.根據0和0計算初步正畸階段數；

步驟3.根據正畸階段數對旋轉量進行Slerp球面插值，對平移量進行線性插值，獲取初始值；

步驟4. 由偵察蜂算法根據初始值生成個初始食物源。

圖6 側切牙插值結果

將人工蜂群算法的初始化方法與牙齒運動理想路徑相結合，對搜索方向加以引導，加快收斂速率的同時并未改變偵察蜂算法的初衷，確保了食物源的多樣性。

3.2 基于優先級策略的牙齒碰撞避免

在正畸過程中，由于牙齒的畸形情況各不相同，且運動狀態各異，根據牙齒不同運動狀態以及不同的錯位情況，將牙齒可能發生碰撞的情況分為圖7中的4類情況。

情況1：2顆牙齒相向運動，其牙根交錯，此類情況在正畸過程中應該避免牙根的碰撞，主要靠牙冠粘貼附件選擇合適的施力方式避免碰撞；

情況2：牙齒朝著同一方向運動，此時為一顆牙齒擋在另一顆前面，且占據了另一顆要去的位置，由于在正畸過程中牙齒是同步移動的，可以優先規劃前一顆，再規劃后一顆牙齒；

情況3：2顆牙齒朝著相反方向運動，此時主要考慮避免牙冠的碰撞情況；

情況4：已經運動到最終位姿的牙齒占據了其他牙齒的路徑，此時被占據路徑的牙齒只能繞路以避免碰撞。

通過分析牙齒碰撞情況可以發現，牙齒運動過程的碰撞只發生于相鄰牙齒之間，不會與其他的牙齒發生碰撞，因此，可以根據各個牙齒與相鄰牙齒的不同情況，制定優先級方案，實現無碰撞的牙齒運動路徑規劃。

優先級方案在多機器人路徑規劃的研究中被廣泛使用[17]，通過為多個運動過程中可能存在沖突的機器人分配運動順序使其避免沖突，即：首先為每個機器人分配一個優先級，然后按照優先級對機器人遍歷，依次為機器人規劃路徑，避免與工作環境中的靜態障礙物和其他機器人發生碰撞。本文參考文獻[18]，在牙齒運動路徑規劃策略中引入優先級方案，從而實現無碰撞正畸路徑。

3.2.1 優先級算法

牙齒的碰撞只會發生在相鄰牙齒之間，因此只需考慮相鄰牙齒間的優先級關系，本文采用的牙齒正畸優先級判定算法是通過相鄰牙齒的位姿距離來判定牙齒間的優先級，即

其中，L0i_0j中的0為牙齒初始位姿序號，m為牙齒理想位姿序號，i為牙齒序號，j為與i相鄰的牙齒；w1，w2為權值，取0.5；為牙齒間的歐氏距離；為牙齒姿態間的四元數距離，越大，表示其角旋轉越相似，同理可計算得到2顆牙齒的目標位姿距離Lmi_mj。以2顆牙齒初始位姿距離與目標位姿距離的差值進行判斷，當時，牙齒間碰撞會出現情況1或情況3，這2種情況說明2顆牙齒優先級相同，即PMi=PMj；當時，此時為情況2，2顆牙齒運動方向相同，需要判斷其位姿前后順序，分別計算牙齒i的初始位姿到牙齒j的目標位姿距離L0i_mj，以及牙齒j的初始位姿到牙齒i的目標位姿距離L0j_mi，若，則PMi>PMj，否則PMi

通過以上策略，遍歷所有牙齒，即可得到牙齒間的優先級關系，其中為牙齒不同的情形分類閾值，為牙齒移動距離閾值，當牙齒移動距離小于時，最后考慮其運動路徑。

3.2.2 優先級判定步驟

判定牙齒之間優先級的具體步驟如下：

輸入：牙齒初始位姿及目標位姿序列，空的牙齒正畸優先級列表；

步驟1. 依次遍歷牙齒；

步驟2. 根據當前牙齒的初始位姿和目標位姿計算其位姿距離0i_mi，若0i_mi≤，則可定義為極小優先級，跳轉至步驟1，否則，繼續步驟3；

步驟5. 遍歷結束，輸出。

3.3 牙齒運動路徑規劃

3.3.1 實際正畸階段數獲取

在生成初始食物源的過程中所獲取的正畸階段數是通過插值所得，考慮的是無碰撞的理想環境。但實際中，牙齒運動很可能會發生碰撞，所以，相較于理想情況，實際規劃過程中的牙齒路徑點數會發生變化，實際的正畸階段數也會大于無碰撞情況下的階段數。

為解決此問題，在雇傭蜂計算適應度函數時，不考慮牙齒移動量和旋轉量約束，在整體規劃完成后，再對每一階段的路徑點按照平移量和旋轉量的約束進行若干個路徑點的劃分，獲取真實情況下的正畸階段數。如圖8所示，點與是2個初始食物源，′和′分別是點和點鄰域內的最佳食物源，由于牙齒運動量約束，會判斷′與′距離超過約束而放棄這2個食物源，那么就會錯過最優值，所以在對食物源進行評價時，不對移動量與旋轉量進行約束，而是在規劃完成后，按照約束對路徑進行劃分，如將′′劃分為′和′ 2個階段。

圖8 路徑點規劃示意圖

3.3.2 牙齒運動路徑規劃步驟

根據本文算法，結合正畸優先級、牙齒運動路徑規劃實際情況，建立牙齒運動路徑規劃步驟：

輸入：待正畸牙齒T初始位姿0i、目標位姿P序列；

輸出：各顆牙齒運動路徑關鍵中間位姿解集PA。

步驟1. 通過Slerp球面及平移量插值對每顆牙齒生成平移量插值1i~(m–1)i、旋轉姿態插值1i~δ(m–1)i；

步驟2.遍歷牙齒，根據優先級方案為牙齒設置優先級，獲取牙齒優先級列表；

步驟3. 根據優先級列表，按照優先級順序對牙齒依次進行路徑規劃；

步驟4. 初始化參數，主要包括路徑點數量、每個食物源搜索最大限制參數、當前迭代次數=0，偵察蜂最大搜索次數，初始種群數量、偵察蜂和觀察蜂分別為=/2，外部存儲PA；

步驟5. 偵察蜂算法生成初始個食物源，然后轉變為雇傭蜂；

步驟6. 初始化當前食物源搜索次數()=0，根據目標函數值計算食物源適應度，將非支配解放入PA中并計算擁擠距離，進行排序；

步驟7. 雇傭蜂局部尋找新的食物源并計算適應度，若優于當前食物源，則更新食物源位置，令次數()=0，更新外部存儲PA，否則次數()自增1；

步驟8. 觀察蜂計算跟隨概率，根據其尋找新食物源，然后轉變為雇傭蜂進行局部搜索，計算適應度，判斷是否更新，并更新開采次數()，更新外部存儲，若()>，則繼續步驟9，否則跳至步驟10；

步驟9. 放棄當前食物源并轉化為偵察蜂，在決策空間隨機產生新的食物源，計算適應度，更新()；

步驟10. 記錄食物源，并更新外部存儲解集，迭代次數自增1，若>，則輸出解集PA，否則跳轉至步驟8。

3.3.3 算法流程圖

算法流程如圖9所示。

圖9 牙齒運動路徑規劃流程圖

4 實驗結果及分析

4.1 牙齒運動路徑規劃結果

實驗中共用20口患者牙齒數據進行了路徑規劃，其中選取患者為18歲男性為樣例，展示執行優化人工蜂群算法后所形成的牙齒矯治方案以及牙齒運動前后位置對比。

如圖10所示，以上頜為例，總共分為39個階段，算法中設置為200次，設置為 4 000次，種群大小為28。篩選出解集中的非支配解形成牙齒運動路徑，展示其中9個中間階段。圖中牙齒上的線段為每顆牙齒的特征線段，可以看出，經過39個階段的平移與旋轉，各顆牙齒逐漸移動至理想牙弓線上，牙齒特征線段也逐漸平滑(圖中被橢圓及矩形標注的牙齒)。圖11展示了各顆牙齒的位姿變化。可以看出，上頜左側中切牙(牙號11)的旋轉量最大，旋轉角為順時針31.3°，兩側側切牙(牙號12，22)移動量較大，分別為2.393 mm與2.418 mm。此例主要移動量集中在前牙、尖牙及前磨牙，而兩側后磨牙移動較少，在實際正畸治療中對后磨牙的矯正難度較大。

圖10 牙齒關鍵中間位置

4.2 不同目標函數實驗結果對比

牙齒移動前后對比如圖11所示，僅以牙齒偏移量為目標函數的規劃結果參數對比見表1，在優化ABC算法中，由于對解集的更新方式進行了改進，提高了種群的分布性，可以獲得更好的解，與基本ABC算法相比，能夠以更小的牙齒移動代價實現牙齒運動路徑規劃，到達理想位姿所需的矯治階段數也更少，從而縮短矯治周期，減輕患者負擔。從表2中可以看出，在目標函數中加入了正畸參數之后，由于優化目標變多，會略微增加牙齒的偏移量，也會稍微增加矯治階段數。但從表3的牙頜參數中可以看出，牙弓對稱度、牙列擁擠度以及Spee曲線深度都有了很好的改善，正畸方案可取得更好的效果，可以說明在目標函數中加入正畸評價參數有利于提高矯治方案的準確性和實用性。與此同時，優化ABC算法的結果優于基本ABC算法，證明本文在提升了ABC算法的種群多樣性之后，能夠獲得更好的優化結果。

圖11 牙齒移動前后對比

表1 僅考慮偏移量的規劃結果

表2 考慮正畸評價參數的規劃結果

表3 牙頜參數對比

5 結束語

本文基于傳統的隱形矯治方案生成方法，提出了新的目標函數，以Spee曲線深度、牙列擁擠度、牙弓對稱度以及牙齒的偏移量為參數，減少了牙齒偏移量，在人工蜂群算法的基礎上加入搜索系數，提高了算法的效率，再對牙齒運動路徑進行規劃。最后在仿真軟件進行測試，并與其他方法進行對比，結果顯示本文方法能較快生成較高準確度的運動路徑，減少牙齒總的偏移量，生成的方案結果更接近理想牙頜，有效縮短矯治周期，具有實用意義。

[1] 盧海麗, 康娜. 無托槽隱形矯治器與固定矯治器對正畸患者牙周健康影響的研究現狀和進展[J]. 口腔醫學研究, 2019, 35(7): 625-628. LU H L, KANG N. Research progress and current situation of influence of Invisalign system and fixed appliances on periodontal health[J]. Journal of Oral Science Research, 2019, 35(7): 625-628 (in Chinese).

[2] 范然, 鈕葉新, 金小剛，等. 計算機輔助牙齒隱形正畸系統[J]. 計算機輔助設計與圖形學學報, 2013, 25(1): 81-92. FAN R, NIU Y X, JIN X G, et al. Computer aided invisible orthodontic treatment system[J]. Journal of Computer-Aided Design ＆Computer Graphics, 2013, 25(1): 81-92 (in Chinese).

[3] GERARD BRADLEY T, TESKE L, ELIADES G, et al. Do the mechanical and chemical properties of InvisalignTMappliances change after use? A retrieval analysis[J]. The European Journal of Orthodontics, 2016, 38(1): 27-31.

[4] 王先澤, 李忠科, 馬亞奇, 等. 一種基于PSO的自動化排牙方法[J]. 計算機工程與應用, 2012, 48(5): 211-212, 238. WANG X Z, LI Z K, MA Y Q, et al. Method of arranging teeth automatically based on PSO[J]. Computer Engineering and Applications, 2012, 48(5): 211-212, 238 (in Chinese).

[5] MOTOHASHI N. A 3D computer-aided design system applied to diagnosis and treatment planning in orthodontics and orthognathic surgery[J]. The European Journal of Orthodontics, 1999, 21(3): 263-274.

[6] 楊光. 牙齒矯正中牙齒移動的仿真和優化方法研究[D].西安: 西安科技大學, 2011. YANG G. Research on simulation and optimization method for tooth movement in virtual orthodontics[D]. Xi’an: Xi’an University of Science and Technology, 2011 (in Chinese).

[7] 張筱. 牙齒正畸路徑規劃方法研究及可視化開發[D]. 濟南: 山東大學, 2016. ZHANG X. Research on teeth orthodontic movement path planning and visual development[D]. Jinan: Shan Dong University, 2016 (in Chinese).

[8] REKOW E D, ERDMAN A G, RILEY D R, et al. CAD/CAM for dental restorations-some of the curious challenges[J]. IEEE Transactions on Biomedical Engineering, 1991, 38(4): 314-318.

[9] 龔誠, 聞娟, 李佳嶺, 等. Spee曲線和擁擠度對口腔正畸模型2D與3D測量法的影響[J]. 口腔醫學研究, 2018, 34(6): 657-661.GONG C, WEN J, LI J L, et al. Influence of Spee’s curve and crowding on 2D and 3D measurement of orthodontic model[J]. Jouranal Oral Science Research, 2018, 34(6): 657-661 (in Chinese).

[10] STANLEY B, WILLAM P, DANA E, et al. The form of the human dental arch[J]. Angle Orthod, 1998, 68: 29-36.

[11] 聶瓊, 林久祥. Angle各類錯(牙合)及正常(牙合)牙弓對稱性分析與比較[J]. 中華口腔醫學雜志, 2000, 35(2): 105-107. NIE Q, LIN J X. Analysis and comparison of dental arch symmetry between different Angle’s malocclusion categories and normal occlusion[J]. China Jouranal Stomatol, 2000, 35(2): 105-107 (in Chinese).

[12] KARABOGA D. An idea based on honey bee swarm for numerical optimization[R]. Kayseri: Erciyes University, 2005.

[13] KARABOGA D, BASTURK B. Artificial bee colony (ABC) optimization algorithm for solving constrained optimization problems[C]//Lecture Notes in Computer Science. Heidelberg: Springer, 2007: 789-798.

[14] DEB K, AGRAWAL S, PRATAP A, et al. A fast elitist nondominated sorting genetic algorithm for multi-objective optimization: NSGA-II[C]//International Conference on Parallel Problem Solving From Nature. Heidelberg: Springer, 2000: 849-858.

[15] HUANG V L, SUGANTHAN P N, QIN A K. Multi-objective differential evolution with external archive and harmonic distance-based diversity measure[R]. Singapore: Nanyang Technological University, 2005．

[16] 畢曉君, 張磊, 肖婧. 基于雙種群的約束多目標優化算法[J]. 計算機研究與發展, 2015, 52(12): 2813-2823. BI X J, ZHANG L, XIAO J. Constrained multi-objective optimization algorithm based on dual populations[J]. Journal of Computer Reasearch and Development, 2015, 52(12): 2813-2823 (in Chinese).

[17] 馬勇. 多移動機器人路徑規劃研究[D]. 武漢: 華中科技大學, 2012. MA Y. Research on path planning of multi-mobile robots[D]. Wuhan: Huazhong University of Science and Technology, 2012 (in Chinese).

[18] 付敬鼎. 隱形矯治技術中的正疇路徑規劃研究[D]. 西安: 西安科技大學, 2018. FU J D, Research on the path planning for orthodontics in invisalign technique[D]. Xi’an:Xi’an University of Science and Technology, 2018 (in Chinese).

Research on path planning of teeth movement in invisible orthodontic

LI Zhan-li, LIU Tong-xin, LI Hong-an, SUN Zhi-hao

(College of Computer Science and Technology, Xi’an University of Science and Technology, Xi’an Shaanxi 710054, China)

Aimed at solving low efficiency and accuracy of path planning of teeth movement in invisible orthodontic schedule, a new method was proposed. First, a new objective function was proposed based on the evaluation parameters of teeth and jaws. Based on the traditional artificial bee colony algorithm (ABC), Pareto solution sets were stored through external storage, and then the Pareto solution set was updated by the improved Harmonic distance, thus diversifying the population. Then, the Slerp spherical linear interpolation and linear interpolation were used to obtain the initial value of the tooth movement path, which was combined with the initial food source generation method in the artificial colony algorithm to generate a better food source. Finally, the new objective function was optimized by the priority scheme of the optimized ABC, leading to the collision-free path for the teeth movement. The experiment showed the effect of the proposed method and compared it with the traditional objective function. The results show that the proposed objective function can generate a more suitable schedule for clinical orthodontic. The improved algorithm can result in a better path and reduce the number of orthodontic stages, and is of practical value.

invisible orthodontic; path planning; artificial bee colony algorithm; multi-objective optimization

TP 391

10.11996/JG.j.2095-302X.2020040556

A

2095-302X(2020)04-0556-11

2019-12-30；

2020-04-14

14 April, 2020

30 December, 2019;

陜西省自然科學基礎研究計劃項目(2019JM-162；2019JM-348)；西安科技大學博士啟動金項目(2019QDJ007)

Natural Science Basic Research Plan in Shaanxi Province (2019JM-162; 2019JM-348); Ph.D Research Startup Foundation of Xi’an University of Science and Technology (2019QDJ007)

李占利(1964–)，男，陜西周至人，教授，博士，博士生導師。主要研究方向為計算機圖形圖像處理。E-mail：lizl@xust.edu.cn

LI Zhan-li (1964–), male, professor, Ph.D. His main research interests cover computer graphics, image processing. E-mail: lizl@xust.edu.cn

李洪安(1978–)，男，山東武城人，副教授，博士，碩士生導師。主要研究方向為計算機圖形圖像處理。E-mail：an6860@126.com

LI Hong-an (1978–), male, associate professor, Ph.D. His main research interests cover computer graphics, image processing. E-mail: an6860@126.com