有限體積格子Boltzmann方法用于近空間連續流區繞流模擬

皮興才，李志輝*，彭傲平，張子彬

（1.中國空氣動力研究與發展中心超高速空氣動力研究所，綿陽621000；2.國家計算流體力學實驗室，北京100191）

1 引言

服役期滿的航天器將再入、解體并進入近空間飛行環境。由于稠密大氣對解體物的氣動力、熱作用，大部解體物會在再入過程中熔融、燒蝕、蒸發消亡掉。但隨著飛行高度、速度、能量不斷降低，至少10%～40%質量的殘骸碎片存留，形成板、方/圓柱、球形物等不同類型的殘骸，隕落到地面，可能對人財物、生態系統安全造成威脅［1-2］。

格子Boltzmann方法（Lattice Boltzmannn Method，LBM）起源于格子氣自動機方法，由Mc-Namara和Zanetti提出［3］，并由Higuera［4］將其應用到實際的流體力學數值計算中。目前已經成為一種新的計算流體力學及數值傳熱學分析方法，被廣泛應用于多孔介質流動、多相流動、微流動等問題分析。

為了保證離散守恒性，標準LBM的平衡態分布函數由Boltzmann方程的經典解析解：Maxwell平衡態速度分布函數作小Ma數Taylor展開獲得。這使得通過Chapman-Enskog展開標準LBM獲得的宏觀流動物理量方程是具有Ma2量級的附加項的不可壓縮Navier-Stokes方程［5］。因此，標準LBM被視為求解不可壓縮流動的壓力修正方法［6］。為了使格子Boltzmann方法能分析可壓縮流動，Shi等［7］提出的求解可壓縮Euler方程的格子Boltzmann模型，Chen等［8］提出的求解可壓縮Navier-Stokes方程的格子Boltzmann模型。但這些模型無法實現比熱比γ的可調，且其還原的比熱比不滿足實際物理意義。Kataoka等［9］提出的多速度格子模型克服了上述問題，并被成功應用到Ma小于1的可壓縮粘性流動模擬。

為了使LBM方法具備高馬赫數可壓縮流動的模擬能力，Qu等［10］提出用圓函數替代經典的Maxwell平衡態分布函數來構造格子Boltzmann離散速度模型，并確保圓函數滿足恢復可壓縮N-S方程所需要的矩關系，成功應用于可壓縮流動模擬。這樣的模型構造思路吸引了眾多研究者：如Li等［11］將其與耦合雙分布函數（Coupled Double Distribution Function，CDDF）Boltzmann模型方程結合，成功應用于Riemann問題、雙馬赫反射、Couette流等經典流動問題的模擬，并實現了普朗特數Pr、比熱比γ任意可調；Qiu等［12］將該方法成功應用于可壓縮邊界層、激波邊界層干擾等流動模擬；Gan等［13-14］采用高階離散平衡態分布函數模型，構造了滿足更復雜動理學矩關系的離散Boltzmann模型，成功將格子Boltzmann方法由可壓縮連續介質流域模擬擴展到Burnett層面的可壓縮近連續流模擬，并揭示了更具普適性本構關系，為高速可壓縮流動中的熱力學非平衡效應研究提供了新的建模思路。

綜上可看出：LBM在求解可壓縮流動方面，已從發展之初的格子氣思想，逐漸過渡到利用Boltzmann介觀思想構造求解流體物理問題的數學關系，并采用格子速度模型進行模型構建階段。但這些可壓縮格子模型在高馬赫數流動中應用案例還鮮有體現。為將LBM推廣應用于服役期滿航天器再入解體殘骸碎片的可壓縮流動問題，本文將構造有限體積格子Boltzmann數值格式，求解耦合雙分布函數模型方程以表征非平衡屬性，并采用以圓函數為基礎發展的D2Q13離散速度模型表征平衡態，由此建立適于近空間連續流區非規則殘骸碎片繞流模擬的有限體積隱式格子Boltzmann方法，并在對Riemann問題、平板雙馬赫反射、RAE2822翼型跨聲速繞流模擬驗證基礎上，開展近空間多次解體形成的殘骸碎片簡化方柱模型超聲速繞流計算及其與N-S方程解算器結果對比檢驗，分析經改進的格子Boltzmann理論模型在模擬近空間連續流區殘骸碎片繞流模擬潛力。

2 理論模型

因耦合雙分布函數Boltzmann模型方程［11，15］的普朗特數Pr、比熱比γ任意可調，且具有良好的數值穩定性，本文采用它作為控制方程。其密度及能量分布函數的演化方程如式（1）所示：

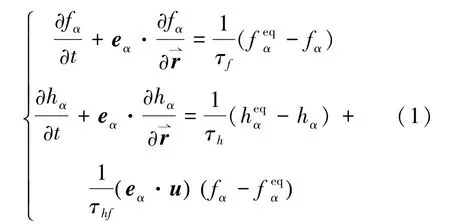
式中，下標α代表不同的離散速度編號，fα是密度分布函數，hα是能量分布函數。是平衡態密度分布函數，是平衡態能量分布函數。eα是離散速度矢量，u是宏觀速度矢量，τf與τh分別是密度分布函數松弛時間及能量分布松弛時間，其滿足關系式（2）：

普朗特數Pr與松弛時間的關系為式（2）：

為了使演化方程通過Chapman-Enskog多尺度展開后能夠還原到可壓縮N-S方程，平衡態密度分布函數及平衡態能量分布函數需要滿足如式（4）所示關系式：

為了滿足上述關系，本文采用基于Qu提出的圓函數重構平衡態分布函數的D2Q13離散速度模型［10-11］。D2Q13離散速度模型如式（5）所示：

其他離散速度點的平衡態密度分布函數滿足式（7）：

各離散速度點的平衡態能量分布函數見式（8）：

3 數值方法

前期應用Boltzmann方程可計算建模氣體動理論統一算法，求解服役期滿航天器解體殘骸的跨流域繞流問題表明：隨著飛行高度降低，解體殘骸碎片再凝固形成的非規則解體物速度迅速降低，呈現近地面連續/近連續流區非規則物形激波/膨脹波多物理場復雜繞流現象［16-17］。因此，引入有限體積隱式格式求解耦合雙分布函數格子Boltzmann模型方程，以保證構造的數值格式具有更好的通量守恒性以及更強的非規則解體物外形適應能力。采用有限體積法處理演化方程式（1）：

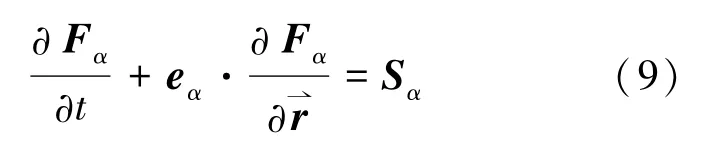
式中，

可得式（11）：

式中，Ωij為結構網格控制體 （i，j） 的體積，及表示F，S在單元控制體內的均值，n為控制體界面沿i，j增大方向的法向單位向量。本文采用NND格式來重構界面通量。因此，式（11）等號左邊第二項可以改寫為式（12）：

式中，Δs為控制體Ωij的邊長。利用Steger-Warming流通矢量分裂，將控制體界面上的通量分解為正通量和負通量，其中正通量由計

（15）：

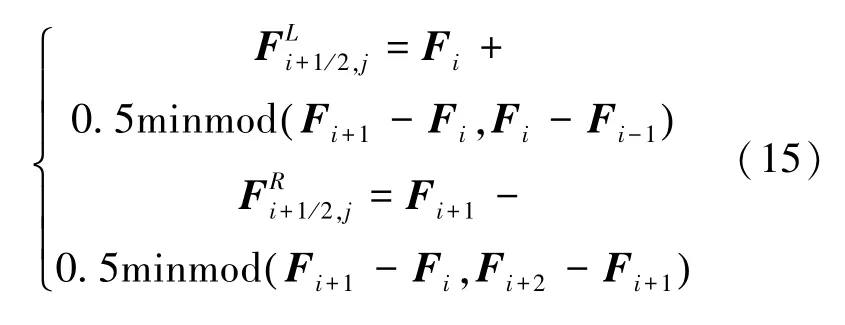
在時間項的處理方面，本文采用多步龍格庫塔法（IMEX-RK）［6，18］。該方法采用顯式方式處理對流項，采用隱式方式處理源項，具有很強的剛性問題處理能力，被成功應用于BGK模型方程的求解。分布函數從第n時間步演化到n+1時間步的公式見式（16）：

式中，上標 ＜n＞表示第n步IMEX-RK變量，l表示IMEX-RK的級數。兩個l×l矩陣a~nn，ann以及l維向量w~n，wn為IMEX-RK方法的系數矩陣及系數向量。文獻［19］對IMEX-RK方法的理論及各階系數矩陣作了詳細的研討。

從式（16）可看出，第n步分布函數的計算需要第n步碰撞項的結果，其是典型的隱式格式。從演化方程式（9）可知，碰撞項包含分布函數、平衡態分布函數及碰撞松弛時間。由此可知，若能獲得第n步的宏觀物理量，此方程可顯式計算第n步分布函數，而不用迭代。值得注意的是Boltzmann模型方程具有質量、動量及能量守恒性，即碰撞項對碰撞守恒量的矩為0。利用該性質可獲得第n步的宏觀物理量：針對式中的密度分布函數分量，在等式各項分別乘以碰撞守恒量φ=（1，eα）T， 并 對 所 有 離 散 速 度 點 求 和 可 得 式（17）［11］：

同理，對能量分布函數進行處理可得式（18）：

由上式可看出，第n步宏觀物理量可通過前幾步的分布函數顯式地計算得出。有了各步的宏觀量，其對應的平衡態分布函數及碰撞松弛時間即可得到。

4 算例驗證與分析

采用上述方法進行Riemann問題、雙馬赫反射等經典問題的模擬，以驗證算法程序可靠性，然后將此算法應用于翼型、方柱模型等近空間多次解體殘骸碎片簡化模型的亞跨超聲速繞流計算。從雙分布格子Boltzmann方程的構造理念可看出，特征溫度的選取并不影響其還原物理量的速度分布函數矩關系。但特征溫度的選取直接影響離散速度點的平衡態分布函數的插值穩定性，進而影響整個數值格式的穩定性。經驗表明，特征溫度的取值一般略大于流場總溫。

4.1 一維Riemann問題

一維Riemann問題流場包含激波、接觸間斷、膨脹波3類典型的可壓縮流動基本元素，流動具有解析解，并且由于流動的一維性，可方便可靠地進行邊界處理，使得考核能夠排除邊界條件對結果的影響，被廣泛用于代碼考核。本數值案例中，定義參考密度ρ0=1.165 kg/m3，參考溫度T0=303 K，參考粘性系數：μ0=1.86×10-5kg/( m·s)，比熱比γ=1.4，普朗特數Pr=0.72，參考速度u0以及參考壓力p0見式（19）：

案例1：SOD問題：

其中，L0=2m，特征時間t0=L0/u0，設定特征溫度Tc=2.5T0，時間步長設為d t=3000·μ0/p0，網格采用Nx×Ny=800×5的均勻網格，且d x=d y=L0/800。在x向邊界處，直接指定宏觀量，并由此得出邊界的平衡分布函數作為邊界條件；在y向，采用周期性邊界條件。圖1展示了在t=0.1644t0的數值計算結果及解析解的對比情況?？煽闯?，除激波后溫度場有稍許偏差外，數值結果整體與解析解吻合良好。

圖1 SOD問題數值解驗證Fig.1 Verification of numerical solution of SOD

案例2：強激波問題

這是一個典型的Colella爆炸波算例，其描述的是激波管隔膜破裂后的流動現象。由初始條件可看出，隔膜兩邊的壓力比大于10萬，對于數值方法的穩定性、空間分辨力提出了巨大挑戰。本算例的基本參考物理量與上例保持一致，特征溫度Tc=1000T0。圖2展示了t=0.012t0的計算結果與解析解的對比情況。整體而言，計算結果與解析解吻合良好。當然，圖中也可看出壓力計算結果在激波后出現振蕩，進一步驗證發現不同的時間及空間格式會產生不同的振幅及頻率，并且一定程度的加密網格可以改善振蕩。密度以及溫度場在激波后與解析解出現稍許的偏離，研究認為這些偏離與空間離散格式有關［11，20］。

4.2 平板雙馬赫反射

服役期滿航天器再入解體過程高溫度梯度致物面附近流動壓縮氣動加熱積累，進入近空間連續流區多次解體殘骸碎片間繞流干擾出現壓縮激波反射嚴重的馬赫桿現象，激波的馬赫反射復雜流動一直是間斷激波多物理場用于理論數值方法檢驗的典型問題。為此，計算馬赫數為10的高超聲速來流以30°的角度入射平面后的流場結構。本算例與一維Riemann問題數值模擬中采用的參考量保持一致。通過本算例，考核本文數值方法對二維可壓縮流動適應性，其物理模型如圖3所示。

計算區域為3 m×1 m的二維矩形域。反射面位于區域底面，反射面采用鏡面反射邊界條件，其余邊界的宏觀物理量根據運動激波關系式給出，密度及能量分布函數在流動入口邊界給定為平衡態，在出口邊界采用外推格式。計算中，特征溫度Tc=85T0。圖4給出t=0.062t0時刻的密度等值線及壓力等值線。由圖看出，計算結果清晰反映了激波馬赫桿，以及第二次反射激波及馬赫桿滑移線。還捕獲到馬赫數及斜劈角較大的情況下出現的第一馬赫桿突出變形現象，馬赫桿在接近壁面時逐漸垂直壁面的流動特點和理論分析吻合，與文獻［21，22］進行對比分析，也可發現相互吻合較好。

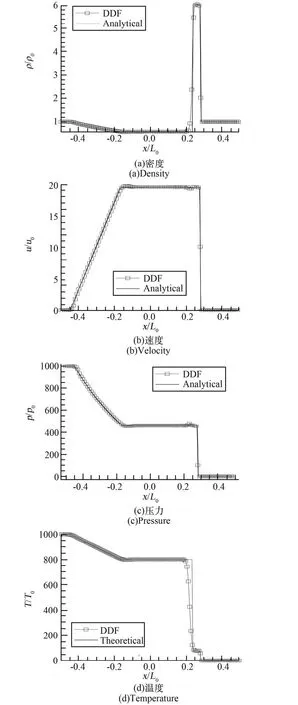
圖2 強激波問題數值解Fig.2 Numerical solution of strong shock

4.3 RAE2822翼型跨聲速繞流問題

RAE2822翼型是典型的二維跨音速流動算例，被16個EUROVAL歐洲合作項目組和AGARD挑選為算法驗證確認流動問題［23］。計算狀態為Ma=0.734，α=2.79°，Re=6.5×106，采用的網格由NPARC官網提供（如圖5），壁面采用非平衡外推方式實現無滑移速度邊界，無窮遠來流邊界條件按Maxwell平衡態分布給定，出口邊界條件由內流場外推，特征溫度Tc=2.5T0。

圖3 雙馬赫反射問題的物理模型Fig.3 Physicalmodel of the double-M ach-reflection

圖4 雙馬赫反射流場密度、壓力等值線Fig.4 Density and pressure contours of the double-M ach-reflection

圖5 翼型繞流計算網格Fig.5 Com putationalmesh for flows around airfoil

圖6繪出該翼型面繞流壓力分布?？梢钥闯?，翼型背部的氣流被加速后，壓力逐步降低。進一步，加速形成的超聲速氣流經過背部激波后減速，壓力陡然回升。由于圖7給出了翼型表面壓力系數分布及其與實驗結果［24］對比情況。可以看出，除了背部湍流轉捩區及激波附著區之外，其他位置計算所得壓力系數與實驗結果吻合較好。

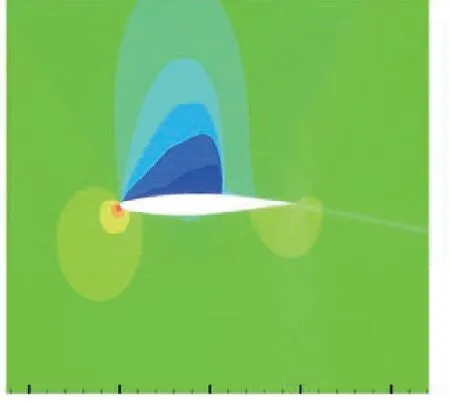
圖6 翼型繞流壓力等值線Fig.6 Pressure contours of the flows around airfoil

圖7 表面的壓力系數Fig.7 Pressure coefficient along the airfoil surface

4.4 解體殘骸碎片類方柱超聲速繞流問題

為考核本文算法在解體殘骸碎片類方柱超聲速繞流問題模擬能力，擬定二維方塊在來流條件飛行高度H=50 km的大氣環境下，以馬赫數Ma=2.0、雷諾數Re=8×104飛行的方塊繞流問題。計算中，特征溫度Tc=4.5T0，無窮遠處來流條件以Maxwell平衡態速度分布給定，出口條件由內流場外推，壁面邊界條件采用鏡面反射滑移邊界條件。圖8展示了本文所發展的耦合雙分布函數有限體積格子Boltzmann方法的計算結果與N-S方程求解結果對比情況（“CDDF”表示耦合雙分布函數有限體積格子Boltz-mann方法結果，“NS”表示NS方法計算結果）。由圖可看出，繞流場密度、溫度、馬赫數分布與N-S方程計算結果整體吻合較好，但在溫度場的尾部回流區，本文計算結果（圖8（b））與N-S結果存在差異。進一步，采用等溫非平衡外推無滑移邊界條件計算結果的尾部回流區溫度場與N-S方程求解器的計算結果吻合良好，由此說明邊界條件對數值計算結果的合理性有明顯影響。隨著馬赫數增加，氣體分子速度分布函數的非平衡屬性顯現明顯，耦合雙分布函數有限體積格子Boltzmann方法的數值穩定性變差，且尾部回流區域稀薄間斷粒子“真空”稀薄效應嚴重，會對數值穩定性產生明顯影響。文獻［25］研究表明，采用更復雜的離散速度模型及多松弛時間演化方程可成功實現馬赫數5的前半圓柱繞流模擬，但具有回流區的高馬赫繞流模擬還鮮有體現，這也反映出格子Boltzmann方法對涉及非平衡效應基于速度分布函數高階取矩宏觀量的溫度、熱流量模擬存在局限性。對于近空間多次解體再凝固板、方/圓柱等殘骸/碎片近地面連續流，因飛行隕落速度很低，基本不存在非平衡效應，為此，本文發展經改進耦合雙分布函數的有限體積格子Boltzmann方法對這類近空間連續/近連續流區殘骸碎片繞流問題模擬具有較好的適應性，進一步的分析確認有待今后開展。

5 結論

本文將有限體積IMEX-RK隱式格式推廣于格子Boltzmann方法，并應用在近空間連續流區非規則航天器解體物繞流模擬，結論如下：

1）采用適用于近空間連續流區殘骸碎片非規則解體物繞流描述的耦合雙分布函數格子Boltzmann模型，使其具有普朗特數、比熱比任意可調。采用圓函數替代Maxwell平衡態分布函數，發展了離散速度模型，拓展了格子Boltzmann方法模擬高可壓縮流動問題能力。

2）采用有限體積法數值離散處理該模型方程以保證構造的數值格式具有更好的通量守恒性及更強的非規則解體物外形適應能力。為了解決源項剛性問題，選用IMEX-RK格式進行時間項離散。在IMEX-RK格式應用中，利用Boltzmann方程具有的碰撞項對碰撞守恒量的矩為零的特點，推導得到了各階宏觀流動量的顯式表達式，避免了隱式求解各階速度分布函數。

圖8 CDDF與N-S方法的計算結果比較Fig.8 Solution com parison between CDDF and N-S solver

3）成功模擬了Riemann問題、雙馬赫反射及翼型繞流問題等案例，驗證了理論模型在可壓流動數值模擬能力，證實IMEX-RK能很好地解決源項剛性導致的穩定性問題。同時看出，所發展方法在模擬高馬赫數復雜高溫度梯度流動方面還存在不足，不同的邊界條件對模擬結果的合理性、數值穩定性會產生影響。本文工作屬初步研究，更精細計算分析驗證有待開展。