再入氣動環境類電池帆板材料微觀響應變形行為分子動力學模擬研究

孫學舟，李志輝，2*，吳俊林，馬 強

（1.中國空氣動力研究與發展中心超高速空氣動力研究所，綿陽621000；2.國家計算流體力學實驗室，北京100191；3.四川大學數學學院，成都610043）

1 引言

運行在低地球軌道環境的板艙桁架式大型航天器在其服役期滿終將面臨離軌再入大氣層解體墜毀的問題［1-2］，因此需要分析評估其對覆蓋空域的人、財、物及生態系統的危害性。該類航天器再入過程經歷高超聲速氣動力/熱壞境［3-4］，會在復雜氣動力熱載荷作用積累下發生軟化熔融解體［5-6］。準確分析這些航天器的再入解體損毀，對可靠預報航天器再入解體殘骸碎片落區，提前做好處置準備工作，將可能的人員傷亡與財物損失風險降至最低等意義重大；而進一步的解體損毀設計則可在確保航天器正常性能的前提下，力爭實現再入過程結構的充分解體燒蝕，減少乃至回避墜落地表的航天器解體殘留物造成的危害。

為實現服役期滿航天器再入過程結構解體墜毀可靠數值預報，需要將跨流域高超聲速的氣動力熱分析同材料結構的實時變形與破壞分析相耦合［4，7-8］。對于跨流域高超聲速的氣動力熱流場計算，李志輝等［9-11］建立了從稀薄流到連續流求解Boltzmann模型方程氣體動理論統一算法（GKUA），給出了精確進行跨流域高超聲速流場計算的方法；彭傲平等［12-13］對GKUA方法進行了發展，實現了對飛行器物面不同位置力、熱流、溫度、速度分布等繞流環境的準確捕捉；馬強等［6，14-15］則基于經典傅里葉導熱定律，建立了高超聲速氣動壞境致結構動態熱力響應變形行為的有限元算法，初步實現了將流場計算同結構變形有限元計算分析的耦合。但這一體系中針對材料在復雜力/熱壞境下的毀壞分析采用的是基于準靜態模型建立的經典材料強度理論分析方法，在航天器再入這樣的極端載荷條件下尚顯不足，而分子動力學模擬方法針對材料微觀尺度的位移及加熱效應對材料力學性能變化與破壞失效分析，預期可進一步模擬揭示其微觀響應行為。

本文針對二組元合金——碳元素質量分數為0.215%的含碳鋼這一類桁架結構大型航天器電池帆板簡化模型平板材料，應用分子動力學模擬其在高超聲速再入氣動環境力/熱載荷作用下的微觀力學行為，分析材料在再入氣動環境不同溫度條件下的力學性能，研究材料在高溫條件下微觀缺陷萌發演化、彈塑性失效過程微觀缺陷萌發演化、彈塑性失效過程，以期為更加準確可靠地通過動態熱力響應有限元算法對服役期滿航天器再入強氣動力熱環境致金屬合金材料結構變形失效熔融毀壞過程模擬奠定基礎。

2 含碳鋼材料模型的建立與驗證

2.1 分子動力學模型的基本晶格模型

本文模擬時所建立的含碳鋼材料的分子動力學仿真模型均是基于具有體心立方晶格（bcc）結構的α-Fe金屬構建，圖1展示了具有體心立方晶格結構的晶胞示意圖。

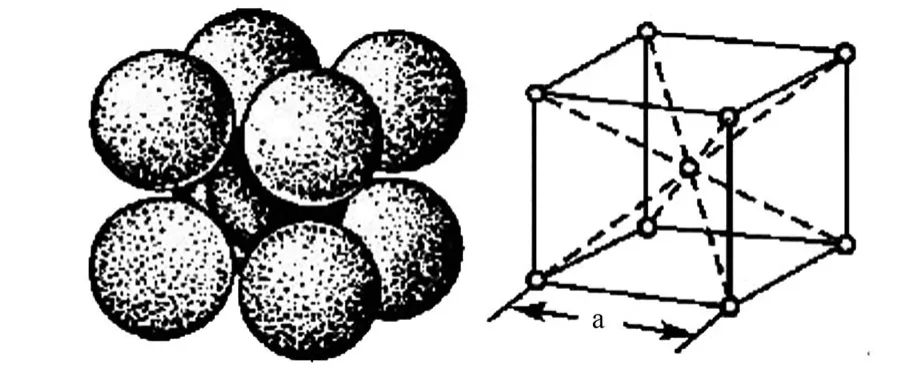
圖1 體心立方晶格結構示意圖Fig.1 The crystal structure of body-centered cubic unit cell

圖中，立方體晶胞的邊長a一般稱為晶格常數，在晶體結構的固體材料中，平衡狀態下的晶格常數a跟隨溫度T的變化規律近似滿足宏觀材料實驗中得出的線膨脹規律，若將不同溫度下材料的平衡態晶格常數與溫度進行線性擬合得其斜率k，則可由式（1）計算得出材料的線膨脹系數α。

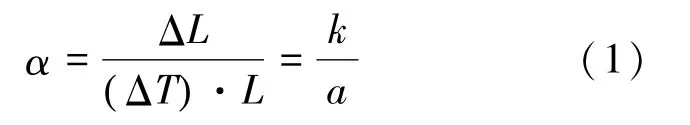
2.2 原子間作用勢

在分子動力學模擬中，用來描述模型內部粒子相互作用的原子間作用勢函數的選用是否合理，對模擬結果是否準確影響較大。根據Rajabpoura等［16］針對單晶鐵和含碳鋼的體模量的平衡態分子動力學計算中不同勢函數的分析，對于含碳鋼體系，選取MEAM勢和Tersoff勢較為合理。本文工作中的分子動力學模擬均采用Liyanage等［17］在2014年提出的MEAM勢函數。所選取的勢函數的系統總能量如式（2）。

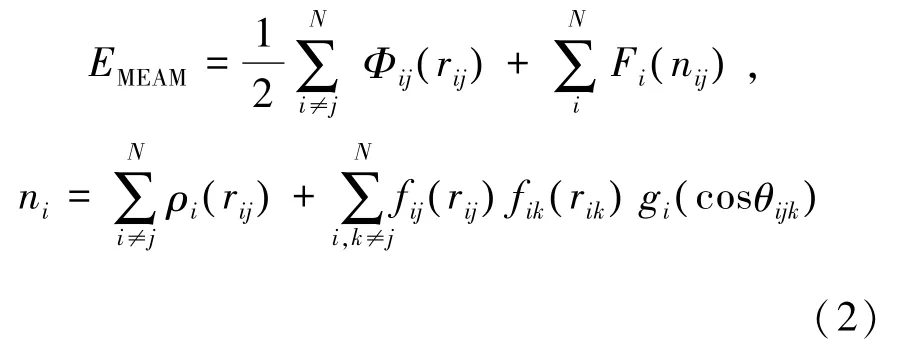
2.3 含碳鋼材料分子動力學模型的建立

參照Rajabpoura等［16］構造合金鋼仿真模型的方法，基于α-Fe金屬晶格結構，構造Fe、C原子數量比99∶1（C元素質量分數0.215%）的bcc含碳鋼材料MD模型，具體構建方法如下：

1）根據模擬所需的晶胞數量，以bcc模型構建對應尺寸的單晶α-Fe，并將這一體系在NVT系綜下進行弛豫，使模型達到平衡；

2）隨機將模型中1%的Fe原子替換為C原子，并用選定的MEAM勢函數描述模型中原子間相互作用，在NVT系綜下充分進行能量最低弛豫，使模型達到平衡，得到含碳鋼MD模擬模型。

2.4 模型與勢函數的驗證

在300～1000 K的不同溫度下，建立一系列原子數量為500的小規模材料模型，采用所選取的MEAM勢函數進行平衡馳豫，以擬合計算材料的主要晶胞平衡態晶格常數以及常溫條件下材料模型的線膨脹系數，以驗證本文所建立的類電池帆板材料模型與描述材料模型內原子間相互作用的MEAM勢函數的合理性。

對材料模型的主要晶胞的平衡態晶格常數擬合計算以常溫條件（300 K溫度）為例，基于2.0?～4.75?的晶格常數構造包含500個原子的周期性邊界類電池帆板材料模型，并都在300 K溫度下以所選取的MEAM勢函數做充分平衡馳豫，至2次時間步間材料模型的總勢能變化小于設定閾值。隨后計算材料模型的晶體結合能，并將模型的晶體結合能與對應的初始晶格常數進行擬合，找出對應最低晶體結合能的晶格常數值，此即為材料模型在300 K溫度下的主要晶胞平衡態晶格常數。

圖2為對300 K溫度下類電池帆板材料模型的晶格常數與晶體結合能的擬合曲線，擬合結果顯示此溫度下，材料模型的主要晶胞平衡態晶格常數為a300K=2.8962?，查閱手冊［18］可得，與模擬的材料模型含碳量相近的20#鋼在20℃（293.15 K）的溫度條件下，主要晶胞平衡態晶格常數為2.8664?，這與本文擬合計算結果吻合很好，相對偏差僅為1.04%。

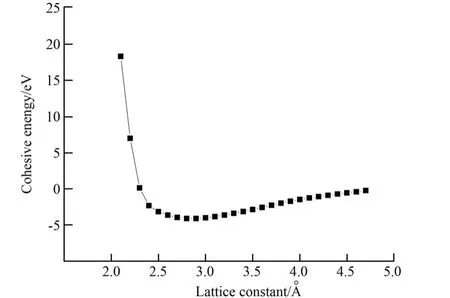
圖2 300 K下晶格常數-結合能曲線Fig.2 Curve of lattice constant and cohesive energy at 300 K

在400～1000 K的不同溫度下，重復上述過程，分別擬合對應溫度下的主要晶胞平衡態晶格常數，將之與溫度進行線性擬合，并根據擬合結果與模擬得到的300 K溫度下材料的主要晶胞平衡態晶格常數，按照式（1）對材料模型在300 K溫度條件下的線膨脹系數α進行計算。

圖3給出了對各個溫度條件下擬合得到的類電池帆板材料模型的主要晶胞平衡態晶格常數與對應溫度進行線性擬合的結果，其中擬合斜線的斜率為k=4.166 12×10-5?/K，根據式（1）可得材料模型模擬所得的300 K溫度條件下線膨脹系數為α300K=1.4385×10-5K-1。查閱手冊［18］，20#鋼的常溫線膨脹系數為 α=1.42×10-5K-1，與模擬結果相對偏差為1.3%，較為接近；同時也與提供本文高超聲速再入環境的計算條件來源文獻［6］在計算鋼制平板這一大型桁架航天器太陽電池帆板的簡化再入模型時所采用的材料系數α=1.5×10-5K-1較為相近，兩者相對偏差4.1%。

通過以上驗證分析，證實本文針對類電池帆板分子動力學材料模型的構建方法與所選取的MEAM勢函數能較為準確可靠描述材料的微觀力學行為，可用于材料力學性能的模擬計算。

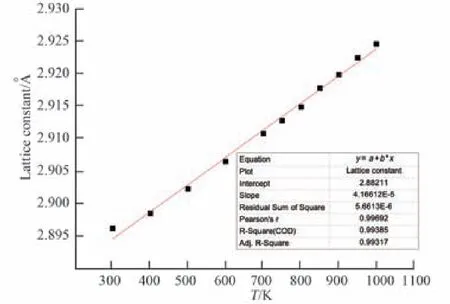
圖3 300～1000 K溫度-晶格常數圖像Fig.3 Curve of tem perature and lattice constant from 300 K to 1000 K

3 分子動力學模擬方法與條件選取

3.1 仿真條件選取

為探究分子動力學在服役期滿大型航天器再入大氣層解體毀壞過程預報領域的應用前景，針對太陽電池帆板簡化模型鋼制平板的含碳鋼材料（碳元素質量分數0.215%），使用分子動力學方法，研究材料的微觀力學響應行為，分析材料力學性能與模型溫度之間的關系，并在極端再入氣動力熱環境下模擬材料的力學性能極限與材料微觀缺陷萌生演化至彈塑性失效過程。在模擬過程中，模型各軸向上均采用周期性邊界條件，以此降低模型尺寸效應對模擬結果的影響，實現用微觀層面模擬得到材料的宏觀力學性能。

在對類電池帆板材料的微觀力學行為與力學性能進行初步模擬時，構造尺寸為10a×10a×10a，包含2000原子的較小規模材料MD模型，在300 K、600 K、900 K、1500 K等不同溫度條件下，分析材料的應力、應變，研究不同溫度下材料模型應力隨應變的變化規律，分析材料力學性能與溫度的關系，為后續再入氣動力熱環境下材料的MD模擬奠定基礎。

在對極端再入氣動力熱環境下材料的力學性能與力學行為進行模擬時，從處在Ma∞=8.37，Kn∞=0.01，γ=1.4的再入高超聲速繞流環境中的服役期滿航天器太陽電池帆板簡化模型：尺寸為0.015 m×0.5 m的鋼制平板變形升溫至穩定的狀態中選取MD模擬條件，其中高超聲速再入平板近連續過渡流繞流流場的溫度與壓力分布通過求解Boltzmann模型方程的氣體動理論統一算法（GKUA）［9-13，19］計算得出，而鋼制平板模型在外流場氣動力熱耦合作用下的變形與平板內部溫度增量分布則由基于熱彈性動力學與熱傳導方程耦合求解材料動態熱力響應的有限元算法（Finite Element Algorithm，FEA）［6，14-15，19］計算給出。

圖4展示了GKUA計算得到的含碳鋼平板在高超聲速近連續過渡流繞流流場的溫度分布情況［6］。分析流場分布可見，迎風面物面附近流場溫度較高，氣流經過拐角后迅速膨脹，進入背風區，流場溫度較迎風區顯著降低，并在后駐點物面達到最低。

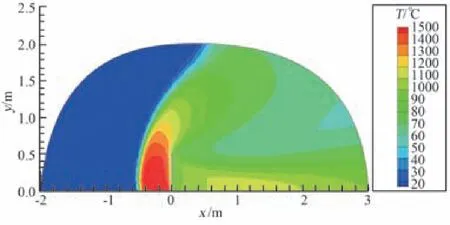
圖4 GKUA計算再入近連續過渡流區鋼制平板繞流流場溫度分布Fig.4 Temperature distribution of re-entry hypersonic flow field of vertical plate in near-continuum transition flow solved by GKUA

圖5給出了使用FEA對處于上述氣動力熱環境中鋼制平板模型進行計算模擬所得到的內部結構場溫度分布，圖中x、y軸的單位為m，模擬中時間步長為δt=0.05 s，結果的單位為℃。明顯可見，模型內部溫度增量較高的區域集中分布在迎風面附近，這與外流場溫度分布規律一致。模型內部溫度增量極大值出現在迎風面左上拐點處，此處邊界曲率發生突變，結合圖4結果可知，外流場熱流也在此處達到最大，與計算結果相符。

對比FEA計算的時間步長δt=0.05 s與MD模擬的時間尺度（一般為ns量級），可認為在每次FEA計算的推進迭代中，MD模擬所關注的微觀尺度材料的力學過程已經經歷了足夠充分的演化發展，因此可以使用具有周期邊界的準靜態MD模擬方法為FEA計算提供較為可靠的當地材料力學性能。從圖4與圖5中分析外流場中平板背風區溫度與平板內部結構溫度增量，可得到含碳鋼平板內部的極限溫度大致在1200～1300 K，由此，本文針對再入氣動環境中類電池帆板材料的力學性能與微觀力學行為的模擬選取在1300 K溫度下，對具有周期性邊界的材料模型施加載荷，并分析加載過程中材料模型中的粒子分布、應力-應變響應等進行分析，以研究材料在這一極端環境條件下的力學性能與失效過程。

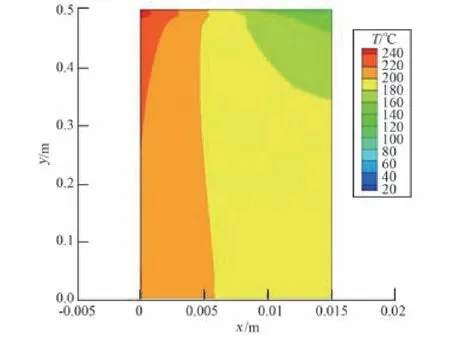
圖5 FEA計算再入鋼制平板內部溫度增量分布Fig.5 Temperature increment distribution in the inner of the p late under hypersonic re-entry flow solved by the FEA

3.2 載荷控制方法

分析不同工況的復雜應力環境中材料的力學性能時，常依照形狀改變比能密度理論（Von Mises第四強度理論），認為畸變能密度達到極限時材料發生屈服，在應力上表現為材料Von Mises應力達到材料的極限。Von Mises應力可以通過式（3）根據材料應力張量的各分量值計算得出。

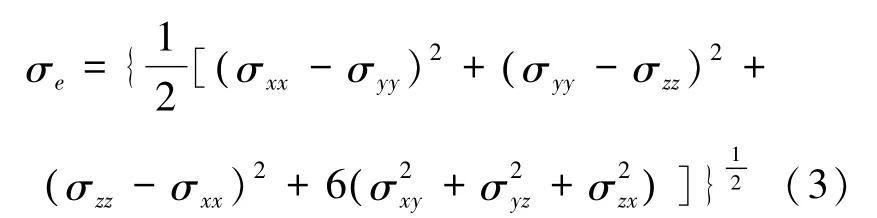
根據這一強度理論，本文選取恒定應變率載荷的單軸拉伸加載方式，來研究復雜受力條件下平板材料模型的Von Mises應力極限。具體加載方式為：將模型與x軸垂直的左端面固定，在右端面上施加大小為ε=2×1010s-1（0.02 ps-1）的恒定應變率的位移載荷，整個加載過程中設置恒溫熱浴控制模型的溫度始終在所設定的模擬溫度附近，并控制材料模型在未施加載荷的y、z方向上外壓為零；加載過程每進行一段時間，就將模型在正則系綜（NVT系綜）下進行一次恒溫弛豫，保持對材料模型的模擬始終處于準靜態，并在每次弛豫后，對模擬體系的微觀特性參數進行輸出。

MD模擬的直接輸出結果為系統內每個粒子在不同時刻的微觀物理量，為此需要通過維里定理對粒子微觀量進行系統平均，得到計算Von Mises應力所需的材料應力張量。維里定理如式（4）所示。

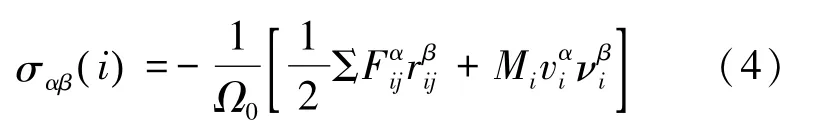
式中，Ω0為原子體積，Fij是第j個原子作用在第i個原子上的力，Mi、vi為第i個原子的質量和速度。

3.3 缺陷演化分析方法

研究材料在MD模擬中微觀缺陷自萌生演化至材料屈服失效的過程時，主要分析材料內部粒子分布情況和材料Von Mises應力隨應變的變化關系。而分析材料內部粒子分布時，除直接觀察可視化處理后材料內部粒子排列，還常通過計算材料徑向分布函數（RDF），進一步分析原子分布的無序化程度。在統計力學中，RDF g( r) 表示距參考粒子r處粒子的密度，若作歸一化處理，則可得到gp( r) 為在r～r+d r范圍內找到一個粒子的幾率。若記p為系統的數密度，則RDF可由式（5）計算得到。

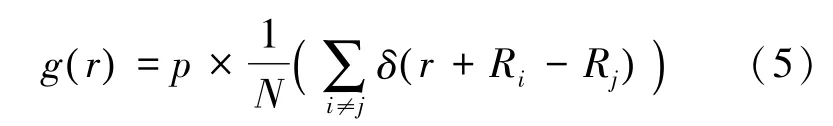
式中，R為原子的位置坐標，δ為Dirac符號，N為原子數。

4 類電池帆板材料的分子動力學模擬

4.1 初步模擬

對不同溫度條件下規模較小（包含2000個原子）的類電池帆板材料模型在單軸拉伸載荷作用下的微觀力學響應行為和力學性能進行模擬分析，并根據材料模擬結果計算分析材料的Von Mises應力與模型總應變的關系，研究并對比不同溫度下材料的力學性能與力學極限，初步確認分子動力學模擬方法在服役期滿航天器再入解體數值預報領域的應用前景與必要性。

圖6繪出了不同溫度條件下模型材料的Von Mises應力隨應變的變化分布曲線，分析不同溫度下材料模型的Von Mises應力隨拉伸方向應變的變化規律，可以發現這些曲線具有相似的非線性變化分布特點。在拉伸過程中，不同溫度條件下材料模型的Von Mises應力跟隨拉伸方向應變的增加均會依次出現3個較為明顯的峰值，并在第三峰值出現后斷崖式下降至一個較小應力值，隨后模型的Von Mises應力在一個較低的應力值附近隨應變的繼續增加而呈現出鋸齒狀波動的特點；在3個峰值中，前兩峰的峰值應力相近，但相對于第三峰的峰值應力而言較小；第三峰為模型材料在模擬過程中材料模型Von Mises應力的最大值，而且在應力隨應變增加達到此峰值之后所表現出的斷崖式下跌與鋸齒狀波動特點與宏觀材料拉伸試驗中觀測到的試樣發生塑性屈服時展現出的應力-應變特性較為相近，由此可為此峰值應力材料模型在對應溫度條件下的塑性屈服極限，在應力達到此峰值后，材料發生了塑性屈服失效。

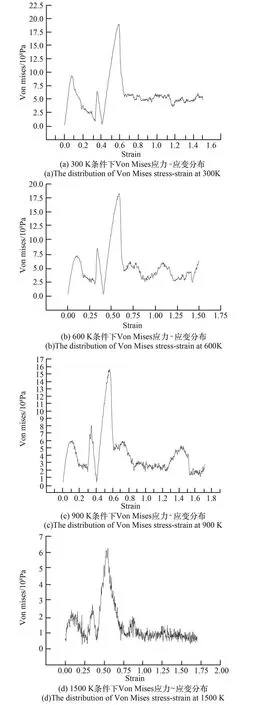
圖6 小規模含碳鋼MD模型不同溫度條件下Von M ises應力-應變曲線Fig.6 Von M ises stress-strain distribution at different tem peratures for small-scale carbon steel

進一步對比分析不同溫度條件下模擬計算的結果，可以發現材料模型的Von Mises應力所對應的塑性屈服極限隨著模型所處的溫度提升而有所下降，在高溫條件下下降尤為明顯。在300 K的溫度條件下，模擬所得的材料模型屈服極限為18.978 024 7×108Pa，所對應的拉伸方向上應變為0.586；溫度升高至600 K和900 K時，材料模型的屈服極限分別下降至18.254 924 3×108Pa和15.643 999 4×108Pa，所對應的拉伸方向上應變分別問0.580和0.566；而當溫度進一步升高至1500 K時，材料模型的屈服極限為6.353 825 4×108Pa，對應的拉伸方向上應變為0.544，此時的塑性屈服極限值剛剛達到常溫條件下的33.5%。

根據3.1節中選取模擬條件時，對高超聲速再入鋼制平板在近連續過渡流繞流環境中內部溫度的分析，鋼制平板模型已經處在1300 K左右的高溫條件中，而對于實際再入大氣層的服役期滿大型航天器來說，其板倉桁架結構在再入強氣動力熱環境作用下變形軟化失效解體的過程中，所面臨的溫度條件將會與之相當甚至更加嚴酷，這意味著分析含碳鋼板乃至服役期滿航天器再入大氣層所遇強氣動力熱環境結構的變形軟化失效解體過程時，極其有必要引入MD方法，模擬分析再入氣動環境計算得到的對應溫度條件下的結構材料力學性能，使用MD實時模擬得到材料內部微觀力學響應行為，為后續有限元算法計算材料結構的溫度梯度與位移變形奠定實時動態氣-固熱力響應耦合模擬基礎。

同時，由于模擬所用的MD模型規模較小，僅包含2000原子，在高溫條件下，由于系統內粒子的能量較高，其相對于平衡位置運動的速度與范圍也比低溫條件有所提升，這使得低溫條件沒有顯現的尺寸效應在高溫狀態有所顯現，第三應力峰出現前原本較為平滑的分布輪廓線段處出現了較多震蕩。因此，要在高溫條件下較為精確模擬材料的微觀響應、力學性能，需要構建較大規模的MD模型，通過統計平均抹平高溫條件下微觀系統的尺寸效應對材料性能模擬帶來的影響。

4.2 再入氣動環境下的分子動力學模擬分析

根據3.1節中選定的再入高超聲速繞流環境類電池帆板材料的MD模擬條件，構建尺寸為80a×30a×30a、原子規模為144 000的MD模擬體系，并在1300 K溫度下施加單軸拉伸載荷，逐步加載至拉伸方向上系統總應變至4.0，分析模擬過程中材料模型的內部粒子分布情況和材料的應力-應變關系，以研究材料在再入高超聲速繞流環境下微觀缺陷萌生演化至塑性屈服失效的過程。

圖7（a）、（b）分別給出了模型經充分馳豫后，加載剛剛開始，系統總應變較小時（加載運行至6250時間步）與材料模型加載至32 500時間步時，材料模型在xy方向截面上的微觀粒子分布情況，圖片使用OVITO（Open Visualization Tool）軟件對模擬結果進行可視化得到，圖中紅色符號代表Fe原子，藍色符號代表C原子，白色空白代表晶狀固溶體結構中的粒子間隙。圖7（a）中，當模型應變較小時，體系內各粒子仍以較為均勻的晶體結構排布，晶格較大；圖7（b）中，體系內粒子的排布較之應變較小時變得相對稠密，晶格變小，模型的粒子排布出現可以觀察到的微觀缺陷，圖中白色符號集聚的區域顯示了微觀層面Fe、C原子在缺陷處變得稀疏，材料模型中微觀缺陷萌生，這些微觀缺陷的延伸拓展導致材料的彈塑性失效以致斷裂毀壞。

圖7 初始運行至32 500時間步時類電池帆板材料模型體系結構中出現較明顯微觀缺陷Fig.7 M icro-defects arisen in themodel system from initial run to Timesteps=32 500

圖8繪出了材料應變逐漸增加過程中，材料模型的徑向分布函數RDF的分布曲線。可以看出，隨著拉伸過程的進行，材料模型RDF中峰的數量逐漸減少；同時峰的寬度逐漸增加，峰的高度不斷降低。這說明隨著材料應變的增加，內部原子分布的有序性逐漸降低，原本完美的空間晶格結構逐漸萌生缺陷。至觀察到明顯微觀缺陷的32 500時間步時，材料模型的RDF曲線中清晰的4個主要峰已經模糊融合成2個，說明此時材料內部原子分布的無序性已經很嚴重，材料內微觀裂隙缺陷已然萌生，隨著這些缺陷進一步的演化延拓，維持材料空間晶格結構的原子鍵團簇破壞，材料逐步開始其彈塑性失效過程，直至軟化熔融徹底毀壞。

隨后對高超聲速再入環境下類電池帆板材料的力學性能極限進行分析，計算材料拉伸過程中的Von Mises應力，并繪制Von Mises應力隨拉伸方向上系統總應變的變化曲線，如圖9所示。可以看出，此條件下對原子數量較大的材料模型進行模擬得到的應力應變關系，與初步模擬時所展現出的應力-應變分布的共性有相似之處，材料的Von Mises應力均跟隨應變增加出現3個峰值后進入鋸齒狀波動增加的塑性屈服階段，且材料對應的塑性屈服極限，亦即模擬過程中得到的Von Mises應力的最大值均出現在第3個應力峰值處，本文模擬所得結果為6.072×108Pa，對應的拉伸方向系統總應變為0.526；但圖9的結果中，與初步模擬得到峰值相近的前兩峰不同，第2個應力峰的峰值明顯低于第一峰，而且在將模擬體系所包含的原子數目極大提升后，高溫條件下由于尺寸效應帶來的震蕩不再明顯，應變在達到第三峰對應的應變之前，圖線的光滑度較之初步模擬有了明顯的提升。

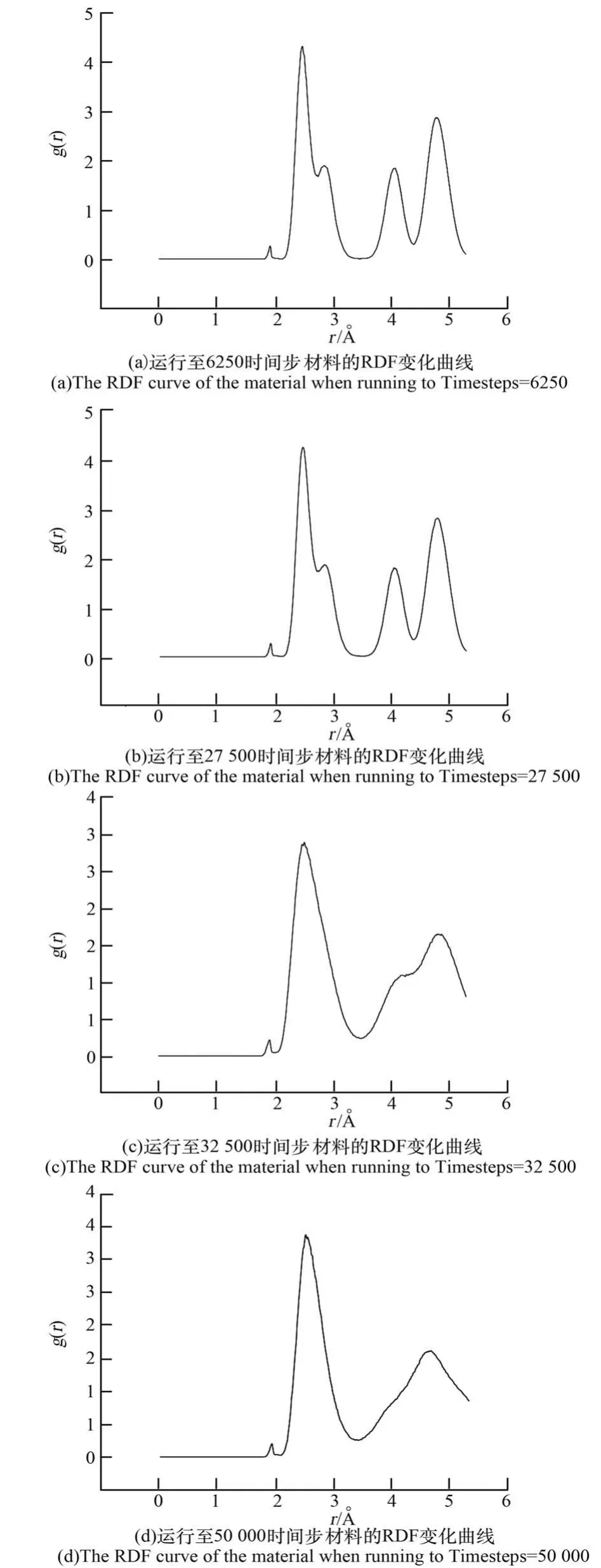
圖8 1300 K溫度條件下模擬得到的類電池帆板材料模型徑向分布函數隨位置距離r變化輪廓線Fig.8 RDF profiles along w ith r of battery-like sailboard material at 1300 K simulated by the present MD model

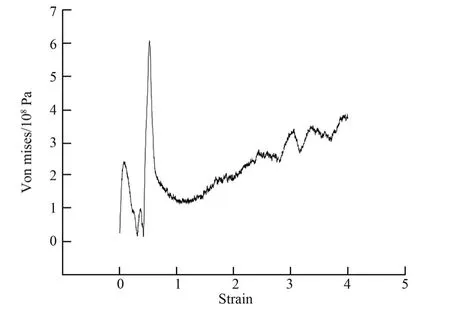
圖9 再入環境類電池帆板材料Von M ises應力-應變曲線Fig.9 Von M ises stress-strain distribution of batterylike sailboard material in the X-direction at 1300 K under reentry environm ent

圖10繪出了由基于準靜態模型建立的經典材料強度理論分析方法的結構動態熱力響應變形行為有限元算法，計算出的鋼制平板模型升溫變形至穩定階段時，平板底部的Von Mises應力分布情況。根據圖示結果，模型內部Von Mises應力在平板底部右下拐點的應力集中處達到極值，此處對應的Von Mises應力已超過9×108Pa，這遠遠超出了本文在對應條件下通過MD模擬得到的材料Von Mises應力強度極限6.072×108Pa。這說明，鋼制平板在高超聲速再入繞流氣動力熱環境中，達到FEA計算結果收斂的穩定狀態前，模型內就已經發生了塑性變形，材料的力學性能發生了不可逆變化；同時說明了服役期滿航天器在其再入過程中，發生首次解體時，航天器太陽電池帆板在高超聲速氣動力熱環境作用下所受應力、溫度還未達到彈塑性失效屈服應力極限與軟化溫度［6，15，19-21］，其原因極可能是其結構材料內部微觀裂隙缺陷萌生演化直至斷裂毀壞，本文嘗試搭建起來的MD模擬平臺初步揭示了這一變化過程，進一步細致研究有待后續深化。為更為細致模擬該平板再入過程的升溫、變形至毀壞的過程，應在模型內Von Mises應力分布極值達到MD計算得到的Von Mises應力強度前，通過FEA計算其結構內部溫度、應力分布，再通過MD方法分析確定對應狀態下的彈塑性模量、線膨脹系數、熱導率等物性參數，作為輸入反饋回FEA計算，將結構材料在再入氣動環境作用下力學性能變化納入結構變形失效分析的過程中，這也為本文所做工作的未來發展指明了方向。

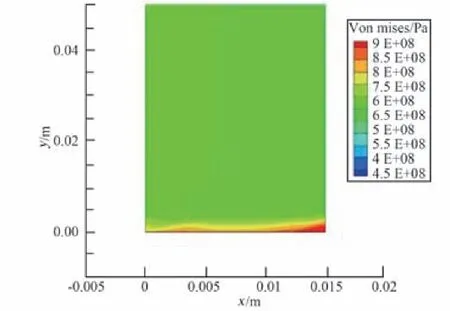
圖10 再入高超聲速環境中穩態時平板底部Von M ises應力分布Fig.10 Von M ises stress distribution of p late at bottom in reentry steady state

5 結論

1）在拉伸載荷作用下，碳元素質量分數為0.215%的二元組分含碳鋼材料模型的Von Mises應力-應變分布具有相似的變化規律，隨著應變載荷的提升，應力依次出現3個峰值，材料在應力達到第三峰值所對應的Von Mises應力強度極限后，進入塑性屈服階段。

2）隨著模型模擬溫度的提升，含碳鋼材料模型模擬得到的Von Mises應力強度極限會降低；在高超聲速繞流環境的條件下，材料模型Von Mises應力的力學性能極限為6.072×108Pa，在應變0.526時達到，這一力學性能極限遠低于通過FEA方法計算出的材料內部應力最大值，說明鋼制平板在達到有限元計算的穩態前，其內部材料就已經發生了塑形屈服失效，力學性能已經發生了不可逆的變化。

3）本文同時通過分析材料模型在加載過程中內部微觀粒子的排列分布變化規律，對材料模型內部微觀缺陷萌生演化發展過程進行了模擬，在具有晶體結構的含碳鋼合金中，隨著載荷的加載，材料內部粒子排布的無序性會增加，局部粒子排布出現空隙，并在此基礎上演化發展為微觀缺陷，直至材料發生塑性屈服失效等宏觀毀壞。

本文所采用的計算模型是較為簡單的二元合金晶體結構，僅包含Fe、C 2種元素組分，在實際的航天應用中，所使用的材料多為組分復雜、工藝特殊材料，作為初步階段性工作，尚難以直接模擬這些復雜金屬（合金）材料微觀力學行為；模擬過程中的加載方式是根據形狀改變比能密度理論以單軸拉伸替代實際工程中的復雜應力條件，這在微觀層面是否完全準確可靠也需要未來進一步驗證確認；同時本文將分子動力學方法引入到金屬桁架結構服役期滿航天器隕落再入過程仿真分析的初步探究，計算規模較小，尚未達到可以實際應用的程度；而如何實現將MD方法與FEA方法進行有機耦合，實現二者計算結果互為輸入，彼此修正，形成閉環，這些是后續深化與發展方向，有待進一步探索研究。