基于四元數理論的2UPS-PU并聯機構位置反解
曹建平,孫文柱,王海東,任 劍
(海軍航空大學,山東 青島 266041)
0 引言
并聯機構位置反解是進行并聯機構運動學分析的第一步。所謂位置反解是已知末端動平臺的位置和姿態反過來求取驅動元件的參數的過程。目前關于并聯機構位置反解的研究主要有矢量法[1]、旋轉換矩陣[2]和旋量[3]等方法。這些方法都可以歸結為基于幾何的矢量分析,當機構結構復雜時求解繁瑣且容易出錯。
本文將四元數理論引入到并聯機構位置反解分析中,利用純四元數表示矢量位置,單位四元數表示矢量的旋轉和方位,從而將并聯機構位置反解的問題轉化為代數推導,以2UPS-PU并聯機構為例闡述了計算過程,并結合MATLAB和SolidWorks仿真來驗證仿真算例。
1 四元數及其在剛體方位描述的應用
四元數[4]是復數的推廣,最早由愛爾蘭數學家哈密爾頓提出。設i、j、k符號滿足下列乘法關系:
i2=j2=k2=-1
(1)
ijk=-1
(2)
則四元數q可定義為
q=a+bi+cj+dk
(3)
其中a、b、c、d為實數,q的共軛四元數為
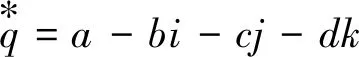
(4)
當a=0時稱為純四元數,此時滿足:
q=bi+cj+dk
(5)
可知純四元數與R3空間點一一對應,同時與三維矢量一一對應,因而可用純四元數來表示矢量的加、減、點乘、叉乘等運算。
當四元數各參數滿足:
a2+b2+c2+d2=1
(6)
此時四元數q稱為單位四元數,也可以表示為
q=cosθ+sinθ(cosαi+cosβj+cosγk)
(7)
R3空間矢量的旋轉可以利用單位四元數q表示。設矢量v1=(x1,y1,z1)′和v2=(x2,y2,z2)′,v2是v1旋轉得到的。在三維空間內描述矢量旋轉需要給出旋轉軸的方位和旋轉的角度,如圖1所示。
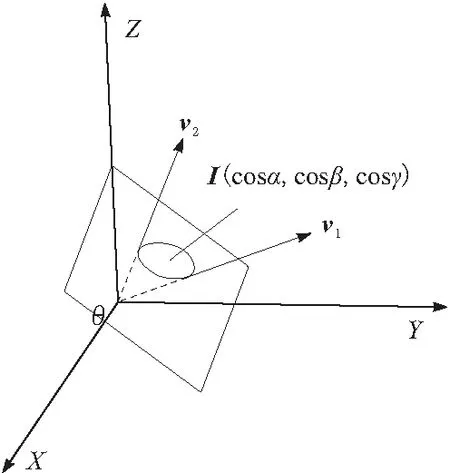
圖1 矢量繞軸旋轉
其幾何意義是:v1繞軸I旋轉θ得到v2,那么已知旋轉軸I的方向余弦I=(cosα,cosβ,cosγ)和旋轉的角度θ即求得v2。這個過程可用四元數進行運算得到,首先利用純四元數表示2個矢量:
qv1=x1i+y1j+z1k
(8)
qv2=x2i+y2j+z2k
(9)
則可得[4]
(10)
其中qR為單位四元數,可表示為
(11)
將qR稱為對應旋轉操作的旋轉四元數。
2 機構描述
基于以上分析,純四元數與單位四元數組合可用于建立并聯機構的運動方程,從而避免了繁瑣復雜的幾何推導,以圖2所示的2UPS-UP并聯機構為例說明。2UPS-UP并聯機構是一種兩轉一移三自由度并聯機器人常采用的構型,在Tricept機器人[5]、四足步行機器人[6]和三自由度并聯搖擺臺[7]等領域應用廣泛。該并聯機構包括動平臺B1B2B3和靜平臺A1A2A3,動平臺B1B2B3通過2個結構完全相同的無約束UPS支鏈和1個恰約束PU支鏈相連,3個支鏈中的移動副作為主動件。該并聯機構存在以下幾何關系:3條支鏈AiBi(i=1,2,3)與動平臺B1B2B3和固定平臺A1A2A3的連接點Bi(i=1,2,3)、Ai(i=1,2,3)呈等腰直角三角形分布,其中B1B2B3的直角邊邊長為e,A1A2A3的直角邊邊長為f;PU支鏈一端通過萬向鉸B3與動平臺B1B2B3相連接,另一端與固定平臺A1A2A3固定連接,PU支鏈與其在靜平臺上的投影的夾角為φ,而投影與固定平臺A1A2A3直角邊夾角為45°。設3條支鏈的長度分別為l1、l2和l3,并分別在靜平臺和動平臺上建立A1-XYZ和B1-UVW直角坐標系。
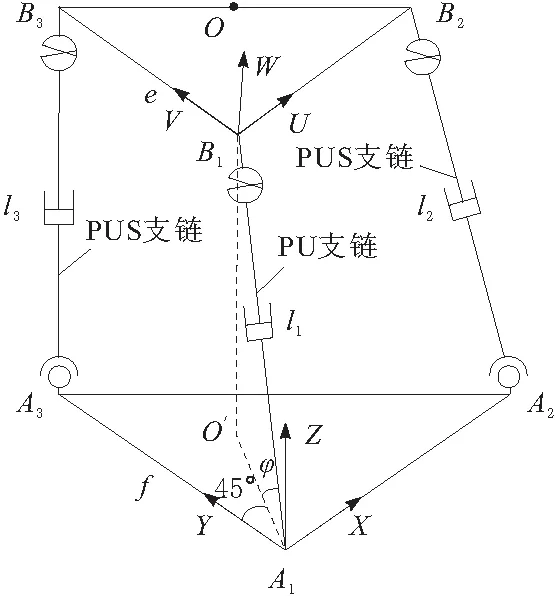
圖2 2UPS-UP并聯機構簡圖
3 基于四元數的機構位置求解
設A1-XYZ的3個正交基矢量集為Γ1={u1,v1,w1},利用純四元數分別表示為
(12)
則在Γ1下,靜平臺的3個連接點A1、A2和A3可用純四元數表示為
(13)
動平臺相對于靜平臺具有2個轉動自由度,首先以X軸為轉動軸逆時針旋轉α,則對應旋轉四元數為
(14)
在qR1作用下,正交基矢量集Γ1轉換為Γ2={u2,v2,w2},將式(14)代入式(10)中,Γ2可用四元數分別表示為
(15)
接著以Y軸為轉動軸逆時針旋轉β,則對應的旋轉四元數為
(16)
在qR2作用下,正交基矢量集Γ2轉換為Γ3={u3,v3,w3},將式(16)代入式(10)中,利用四元數分別表示為
(17)

(18)
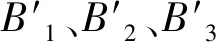
(19)
則動平臺的3個連接點B1、B2、B3可用四元數表示為
(20)
則支鏈L1、L2和L3可用四元數表示為
(21)
將式(13)、式(18)、式(19)和式(20)代入式(21),可得
基于以上推導可完成2UPS-PU并聯機構的運動位置反解,即已知執行平臺的位置和方位計算動力元件參數。在2UPS-PU并聯機構中,動平臺有3個自由度,以動平臺B1為基準點,設其距靜平臺垂直高度為h,用上文提到的α和β表征動平臺的方位,則2UPS-PU并聯機構3條動力支鏈的長度l1、l2和l3可表示為
(23)
將式(22)代入式(23)后可得
(24)
式(24)即為2UPS-PU并聯機構的反解方程。
4 仿真算例驗證
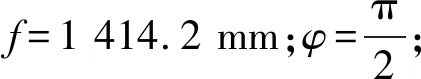
(25)
將h、α和β分別代入式(24)中,利用MATLAB仿真,設置步長為0.1,可得到l1、l2和l3的變化規律如圖3所示。
利用SolidWorks建模,給出2UPS-PU并聯機構的CAD三維模型,并利用Motion插件進行運動仿真,如圖4所示。將反解得出的l1、l2和l3分別作為圖4所示直線馬達1、直線馬達2和直線馬達3的運動輸入參數,仿真時間為32 s,并設置動平臺的中心記錄其運動路徑并保存為計算結果。
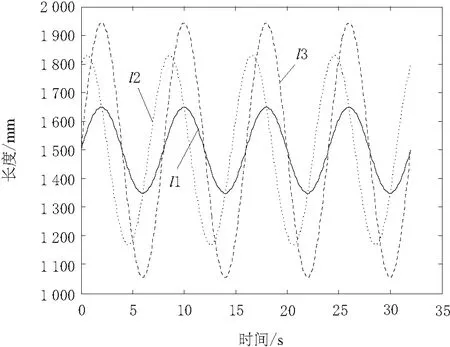
圖3 并聯機構算例的位置反解結果

圖4 并聯機構的CAD三維模型及驅動
圖5給出了并聯機構在第1秒、第3秒、第6秒和第10秒的仿真運動可視化結果,10 s后動平臺進行周期性運動。圖5d給出了第10秒中心點的完整運動軌跡圖。
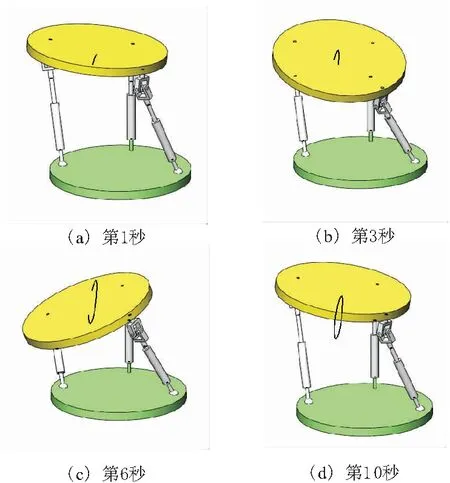
圖5 SolidWorks軟件的仿真可視化結果
將圖5所示的中心運動軌跡的數值結果從SolidWorks中取出,為進行對比每隔5個數進行平均篩選,并在MATLAB中繪出,得到的仿真軌跡結果如圖6所示。
分析如圖2所示的動平臺中心點的理論運動軌跡,動平臺中心點O位于動平臺B1B2B3的斜邊中點上,則其位置可用純四元數表達為
(26)
代入式(17)~式(20)后,可得
(27)
在坐標系Γ1下,可表示為
(28)
將式(25)及相關的結構參數代入到式(28)中,設置步長為0.1,可得到中心點O的理論軌跡如圖6實線所示的理論軌跡結果。
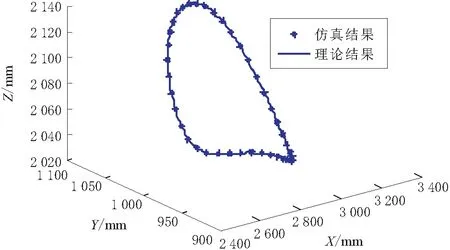
圖6 動平臺中心的理論軌跡與仿真軌跡對比
由圖6可知,該方法的理論結果與仿真結果一致,從而說明了基于四元數理論的2UPS-PU并聯機構的位置反解方法的正確性和有效性。
5 結束語
將四元數理論用于2UPS-PU并聯機構位置反解,從應用過程得出以下結論:
a.利用四元數理論推導得出2UPS-PU并聯機構位置反解方程,相對于傳統幾何方法,該方法直觀易于理解。
b.利用MATLAB和SolidWorks Motion驗證了結果的正確性。
c.該方法具有一般性,可推廣至其他任意并聯機構。

