方位安裝誤差對調平性能的影響及對策

張 濤，魏貴玲，馮 波，陽 洪，魏旭陽,陳 超,王 斌

(1.中國電子科技集團公司第二十六研究所，重慶400060;2.四川交通職業技術學院，四川 成都611130；3.中電科技集團重慶聲光電有限公司，重慶401332)

0 引言

調平系統作為各類車載平臺的調平支撐組件，為智能化、高機動車載裝備、民用精密車載儀器、氣象雷達等提供高精度的水平基準。調平系統利用水平傳感器原理和伺服控制技術原理，將電氣伺服控制、機械結構、水平傳感器融合為一個有機整體，由電機、驅動器、控制計算機組成的專門伺服調平控制組件帶動傳動機構自動采集車輛傾斜狀態并完成車輛調平。水平傳感器利用傳感器在重力場中能敏感重力加速度的原理，在載體傾斜時自動測量傾角的變化。調平系統工作時，為了避免輪胎變形引起平面變化，保證調平后的水平度，首先使輪胎離地，讓調平腿支撐車輛，再根據采集到的車輛傾斜狀態，通過算法控制調平支撐腿的運動并最終達到調平精度[1]。本文的研究對象是風吹、人員走動和車輛發動機抖動等動態條件下的水平傳感器方位安裝誤差。動態水平傳感器安裝在設備重點調平的位置，可以在姿態搖擺狀態下使用。高精度的設備對調平系統提出了更高要求,但實際工程中易忽視動態水平傳感器的軸系安裝誤差。

1 自動調平系統

由于載車形式的多樣性(如直掛車、半掛車等)，平臺的形式、大小、承重、剛性的差異等，機械電控形式調平支撐通常有四、六點調平等，調平精度指標的實現，與水平傳感器的精度、設置方式、數量不同有關。其中，四點調平是當前主流裝備普遍采用的形式，運用較廣泛的是類似模糊控制的模式，即調平支撐腿的運動只要有利于水平度的改善即可[2]。調平系統工作時由水平傳感器傳遞角度信號給控制系統[3]，控制系統通過控制電機、傳遞系統實現對平臺的精確調平，并通過電機制動器的制動，對調平后的支撐系統進行長時間的鎖定[4]。水平傳感器本身誤差對調平精度的影響已有討論，本文以四點支撐調平方式為例，分析了動態水平傳感器方位安裝誤差對調平精度的影響。為了使后述的調平方式有確切的理論依據，現對四點支撐的調平平臺做力學分析，在分析過程中做以下3點假設，即

1) 平臺為剛性。在調平過程中平臺不會發生形變。

2) 調平支撐腿剛性。在調平過程中支撐腿不會發生形變。

3) 地面剛性。調平過程中地面保持水平高度,不因壓力而產生變化，土地松軟不在此假設范圍內。平臺支撐腿模型簡圖如圖1所示。

圖1 四點支撐平臺系統簡圖

現對平臺需用到的變量設定如下：車載平臺所載物總質量為M，以平臺左下調平支撐腿中心點為原點建立水平坐標系，水平軸為X軸，垂直軸為Y軸，X方向兩調平支撐腿的中心點間距為La，Y方向兩調平支撐腿的中心點間距為Lb。

在調平過程中，利用動態水平傳感器測量得到偏離水平面的兩個角α、β(約定平臺處于近似水平狀態，即α、β均小于3°)，調平的目標是使平臺表平面和大地水平面重合，最終使α、β均為0°。

設繞X方向旋轉的傾角為α，繞Y方向旋轉傾角為β，則存在兩個平面(平臺表平面和大地水平面)。假定兩個坐標系中水平面坐標系為OX0Y0Z0，理想平臺表面坐標系為OXbYbZb，則非水平狀態下的平臺坐標圖如圖2所示，兩坐標系間的變換矩陣為

(1)

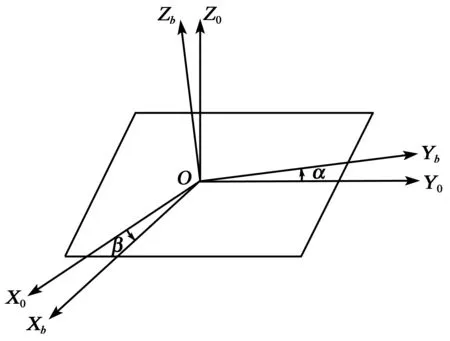
圖2 非水平狀態下的平臺坐標圖

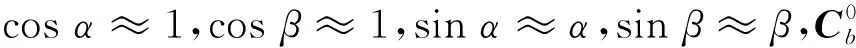
(2)

假設第i個調平支撐腿在水平坐標系OX0Y0Z0中的坐標位置0Pi=(0Pix,0Piy,0Piz)，在平臺表面坐標系OXbYbZb上的坐標bPi=(bPix,bPiy,bPiz)，則可得

α×bPiy+bPiz

(3)

各調平支撐腿的支點初始位置為

0Piz=β×bPix+α×bPiy

(4)

通過式(4)可得到一個最高點，設I=h(其中I為假設的最高點，h為其余3點與最高點的高度差)為最高點位置，另3條支撐點做與最高點位置差值的伸腿動作，當完成位置差值的伸腿動作后，平臺達到水平。各支點與相對高點的位置差為

ei=β×(bPhx-bPix)+α×(bPhy-bPiy)

(5)

若3點為最高點，則各個支點坐標分別為1(0，0)、2(La, 0) 、3 (La,Lb) 、4 (0,Lb), 代入式(5)可得

e1=β×La+α×Lb

(6)

e2=α×Lb

(7)

e3=0

(8)

e4=β×La

(9)

總調節距離為

(10)

由式(6)～(9)可得S。調平時經多次調整使X、Y軸的傾角誤差逐漸減小，直至達到水平精度指標要求。

2 動態水平傳感器

動態水平儀基于慣性導航技術[5]，為調平系統提供α和β。其工作原理是通過陀螺測得的載體角速度信息和加速度計測得的載體加速度信息進行模/數轉換后被送入導航計算機，導航計算機對數據進行誤差補償[6-7]、對準、導航解算和卡爾曼濾波，最終得到載體縱橫搖角(α,β)。動態水平傳感器工作原理框圖如圖3所示。

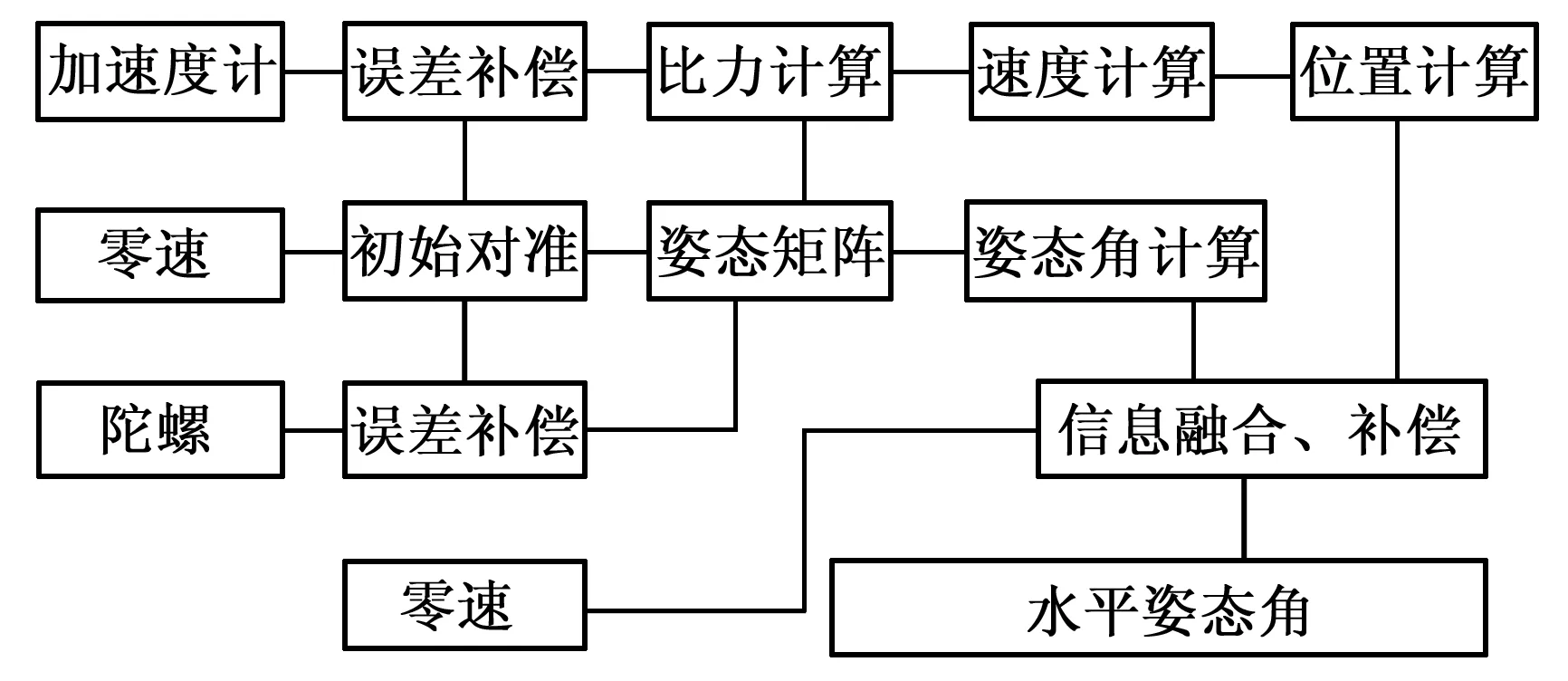
圖3 動態水平傳感器工作原理框圖

3 方位安裝誤差影響分析

在實際自動調平系統中會存在繞平臺表平面垂直軸方向旋轉的安裝誤差，設此安裝誤差為δφ，含有安裝誤差的實際測量表面坐標系為OXb′Yb′Zb′。則OX0Y0Z0、OXbYbZb和OXb′Yb′Zb′的關系如圖4所示。

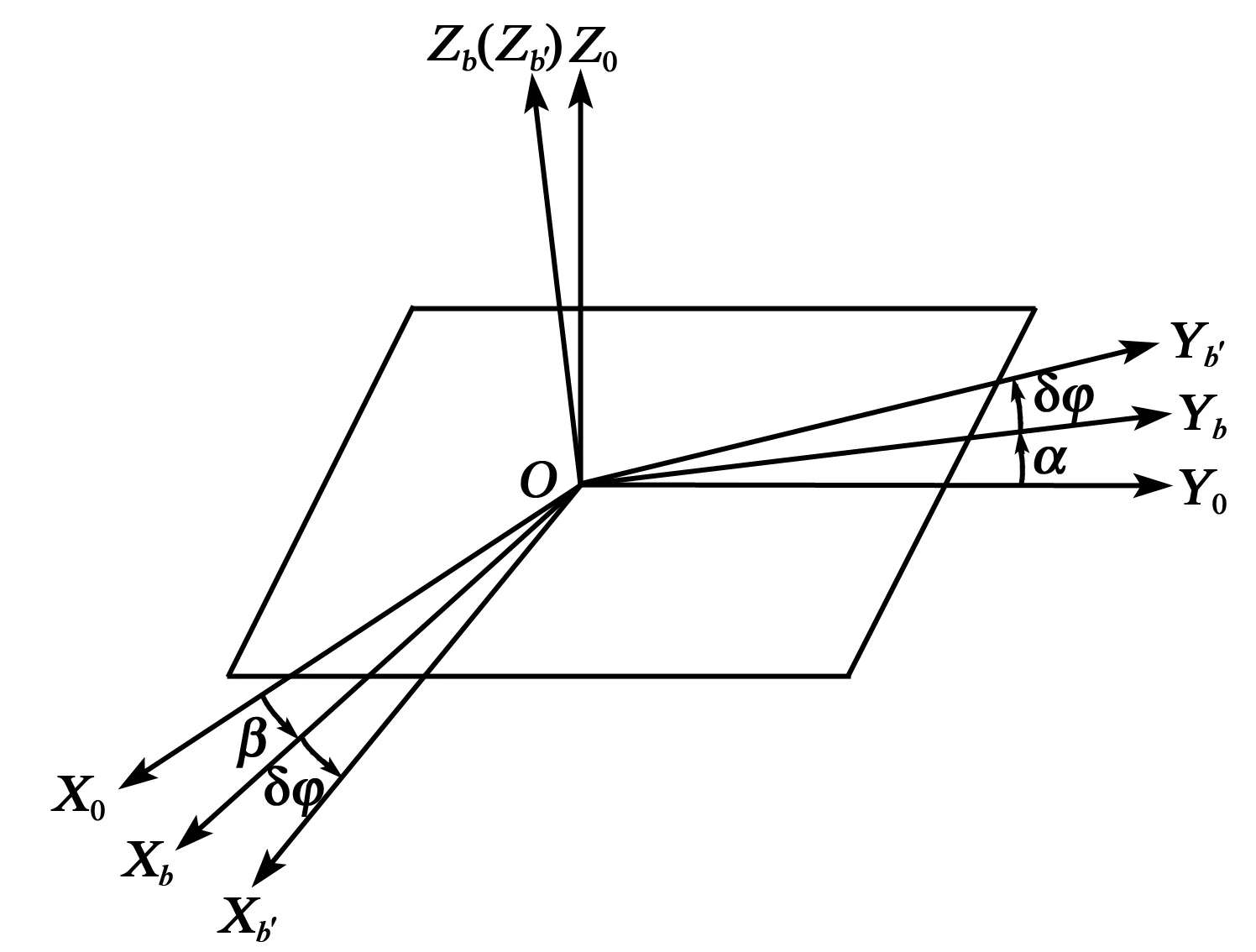
圖4 坐標的關系圖

3個坐標系的關系為

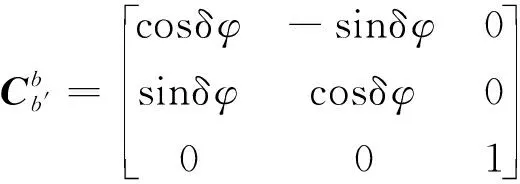
(11)

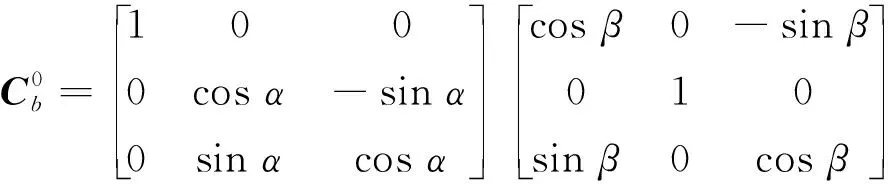
(12)

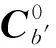
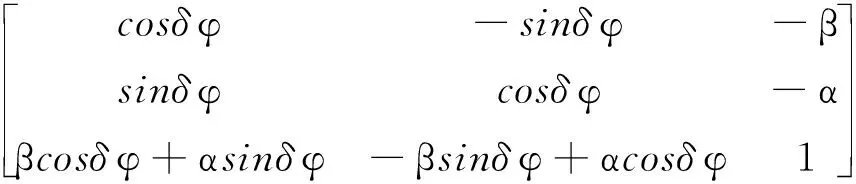
(13)

測量平面坐標系中第i個調平支撐腿在水平坐標系中的坐標位置0Piz為

(αcos δφ-βsin δφ)×b′Piy+b′Piz

(14)

若存在方位安裝誤差角，得到的各支點的初始位置為

0Piz=(βcos δφ+αsin δφ)×b′Pix+

(αcos δφ-βsin δφ)×b′Piy

(15)

由式(11)～(13)推導得到式(14)坐標位置和式(15)初始位置，然后可以求出各支點與相對高點的位置差值，即位置之差為

ei=(βcos δφ+αsin δφ)×(b′Phx-b′Pix)+

(αcos δφ-βsin δφ)×(b′Phy-b′Piy)

(16)

同樣地，若3點為最高點，則各個支撐點坐標分別為1(0,0)、2(La, 0) 、3(La,Lb) 、4(0,Lb), 代入式(16)可得

e1=(βcos δφ+αsin δφ)×La+

(αcos δφ-βsin δφ)×Lb

(17)

e2=(αcos δφ-βsin δφ)×Lb

(18)

e3=0

(19)

e4=(βcos δφ+αsin δφ)×La

(20)

對比式(6)～(9)和式(17)～(20)可知，當δφ存在時，δφ會影響調平系統的調節過程。

4 仿真分析

采用仿真實驗可知δφ對調平系統的影響，仿真條件為La=3 m，Lb=2 m，α=1°，β=-2°。δφ在0°～360°變化過程中,動態水平傳感器的δφ引起的各支撐點控制量誤差如圖5所示。由圖可知，動態水平傳感器的δφ會造成調平各支撐點的控制量誤差。

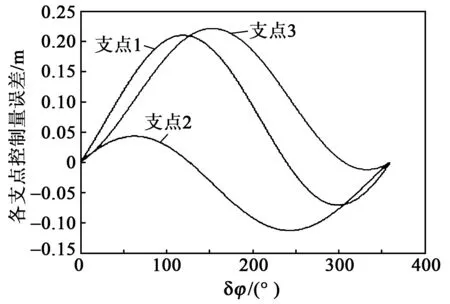
圖5 各支點控制量誤差仿真圖

5 測試及試驗

綜上所述，δφ會導致各支點的控制量變化。當δφ≤3°時，可得各支點的控制量誤差如圖6所示。

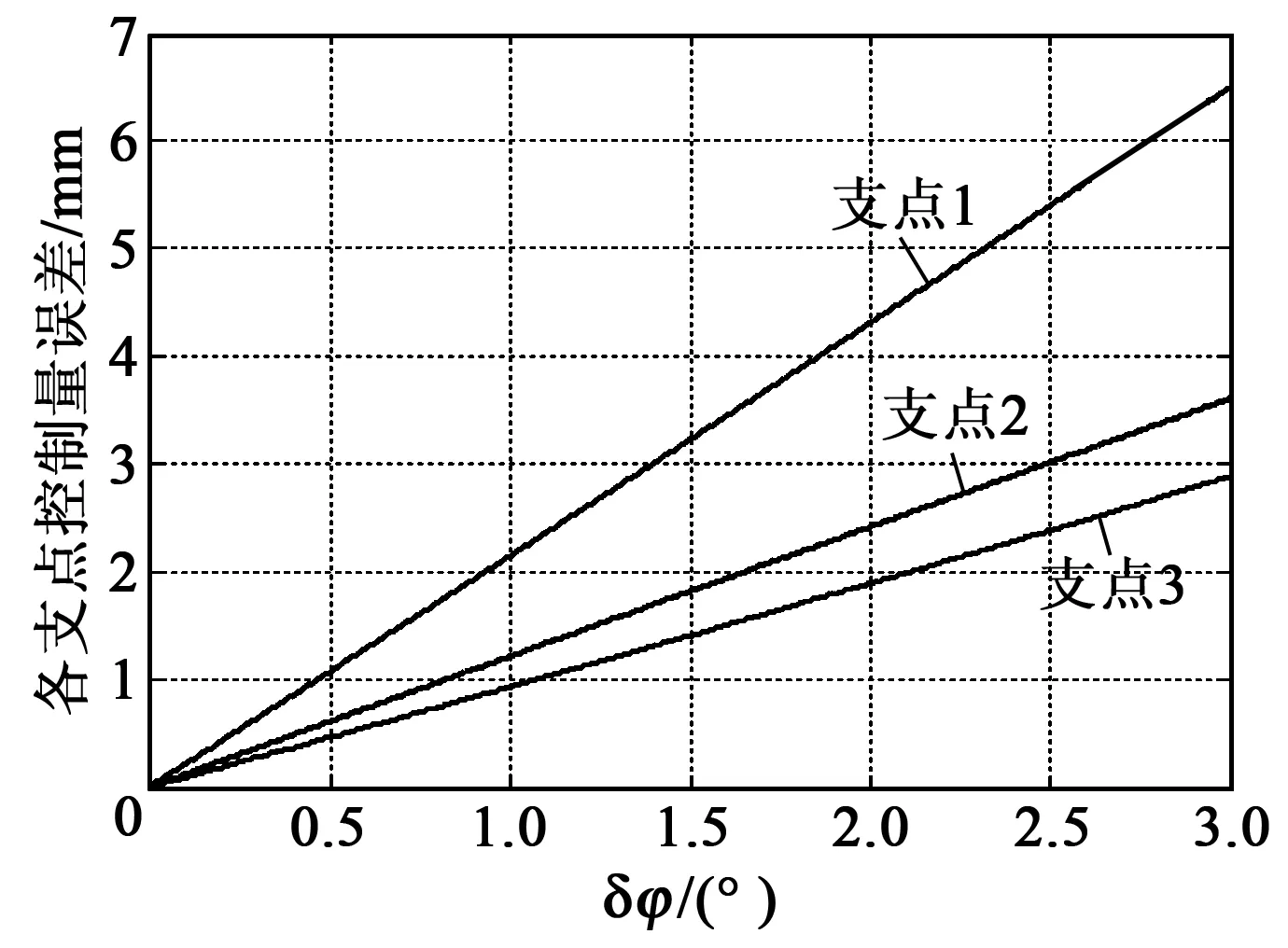
圖6 方位角度誤差導致控制量誤差分析圖

由圖6可知，各個控制量誤差隨δφ呈線性增長。我們將水平傳感器安裝在α=3°，β=-2°的初始點，δφ=3°、1°和0.5°時，通過測試得到的影響結果如表1所示。

表1 δφ對調平次數的影響表

由表1可知, δφ和調平控制次數相關。水平傳感器的δφ越小，總調節次數也隨之減少。當δφ=3°時，通過3次調節才能達到1′的調平精度。當δφ≤1°時，只需要2次就能達到調平精度。試驗結果表明，δφ對調節次數、調平時間和調平精度有明顯影響。

6 結束語

在工程中使用動態水平傳感器時，通過測試儀器盡量使動態水平傳感器的軸系與安裝基座軸系平行，減小了方位安裝誤差角，提高了調平速度，改善了控制性能。