基于正逆向解算的單軸旋轉(zhuǎn)慣導(dǎo)參數(shù)辨識方法

王靈草,陽 洪，胡小兵，張 裕

(中國電子科技集團公司第二十六研究所, 重慶 400060)

0 引言

在單軸旋轉(zhuǎn)光纖陀螺慣導(dǎo)系統(tǒng)中，由于慣性測量單元繞方位軸旋轉(zhuǎn)，水平常值及慢變陀螺漂移被調(diào)制，與捷聯(lián)慣導(dǎo)系統(tǒng)相比，其導(dǎo)航精度將大幅提高，但旋轉(zhuǎn)軸陀螺漂移不能被調(diào)制補償，成為影響導(dǎo)航精度的關(guān)鍵因素[1]。因此，估計并補償旋轉(zhuǎn)軸z軸陀螺漂移對單軸旋轉(zhuǎn)慣導(dǎo)系統(tǒng)至關(guān)重要[2]。另外，在慣性導(dǎo)航系統(tǒng)實際應(yīng)用中，為了提高載體的快速反應(yīng)能力和機動能力，常要求慣導(dǎo)系統(tǒng)能在最短時間內(nèi)為載體提供滿足指標(biāo)要求的姿態(tài)基準(zhǔn)和導(dǎo)航結(jié)果。而在慣導(dǎo)系統(tǒng)對準(zhǔn)過程中，對準(zhǔn)精度需要更長的對準(zhǔn)時間來保證。為了縮短對準(zhǔn)時間并提高對準(zhǔn)精度，且能夠辨識出z向旋轉(zhuǎn)軸陀螺漂移，本文提出了一種適用于靜基座條件下的參數(shù)快速辨識方法，該方法基于時間正逆向解算算法[3-4]，通過建立開路法航向角誤差模型，增加航向角量測量，利用最小二乘算法實現(xiàn)了初始姿態(tài)的確立和z向陀螺漂移的估計。

1 參數(shù)辨識對準(zhǔn)算法

1.1 慣性系坐標(biāo)系定義

1) 慣性坐標(biāo)系(i系，OXiYiZi)。原點位于地心的慣性空間。

2) 地球坐標(biāo)系(e系，OXeYeZe)。e系相對i系的角速率為地球自轉(zhuǎn)角速度ωe。

3) 導(dǎo)航坐標(biāo)系(n系,OXnYnZn)。選取當(dāng)?shù)氐乩碜鴺?biāo)系為導(dǎo)航系，原點O位于載體所在位置，Xn、Yn和Zn分別指向東向、北向和天向。

4) 旋轉(zhuǎn)坐標(biāo)系(p系)。原點位于電機旋轉(zhuǎn)平面內(nèi)，z為電機旋轉(zhuǎn)軸，x由x陀螺敏感軸在垂直z的平面內(nèi)的投影所確定，y由右手定則確定。

5) 初始時刻旋轉(zhuǎn)單元體慣性坐標(biāo)系(ip0系)。初始對準(zhǔn)t0時刻，ip0系與p系重合，初始對準(zhǔn)開始后ip0系不隨載體或旋轉(zhuǎn)體轉(zhuǎn)動，在慣性空間指向不變。

6) 初始時刻慣性凝固坐標(biāo)系(i0系)。初始對準(zhǔn)t0時刻，i0系與i系重合，初始對準(zhǔn)開始后，在慣性空間指向保持不變。

1.2 對準(zhǔn)算法結(jié)構(gòu)

靜基座條件下，基于數(shù)據(jù)存儲的正逆向計算對準(zhǔn)算法的時間結(jié)構(gòu)框圖如圖1所示。首先利用實時采集的陀螺和加速度計數(shù)據(jù)進行基于慣性系初始姿態(tài)角的粗對準(zhǔn)，在實時粗對準(zhǔn)過程中，同步壓縮每秒的陀螺加速度計信息并將其存儲；待粗對準(zhǔn)結(jié)束后，再利用存儲的數(shù)據(jù)進行基于正逆向計算的參數(shù)辨識精對準(zhǔn)，直至對準(zhǔn)結(jié)束。

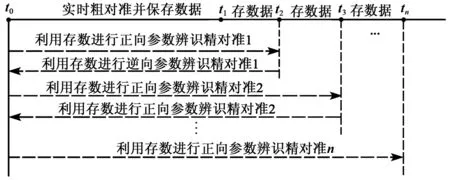
圖1 基于時間正逆向計算的靜基座快速對準(zhǔn)算法結(jié)構(gòu)圖

由于濾波需要消耗時間，因此在逆向解算過程中還需要繼續(xù)采集陀螺、加速度計數(shù)據(jù)并保存關(guān)鍵數(shù)據(jù)，直至t2時刻(濾波計算時間與陀螺加速度計的實時采樣時間相遇時刻)；再利用[t0,t2]段保存的數(shù)據(jù)進行逆向參數(shù)辨識精對準(zhǔn)，依次進行下去直至對準(zhǔn)結(jié)束。

1.3 靜基座對準(zhǔn)參數(shù)辨識粗對準(zhǔn)模型

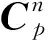
(1)

(2)

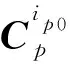
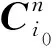
(3)

式中Δλ=λt-λ0為相對t0時刻的經(jīng)度變化量，靜基座對準(zhǔn)時Δλ=0，行進間對準(zhǔn)時λt可由GPS經(jīng)度提供。

根據(jù)雙矢量定姿原理可得：

(4)

式中tk1，tk2指對準(zhǔn)過程中的k1、k2時刻；v為速度矢量。其中：

vn(t)-gn}dt

(5)

(6)

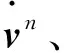
1.4 粗對準(zhǔn)過程中壓縮保存關(guān)鍵數(shù)據(jù)方法

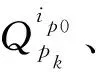
(7)

式中I為單位矩陣。

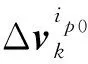
(8)

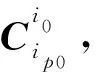
1.5 靜基座對準(zhǔn)參數(shù)辨識精對準(zhǔn)模型

基于正逆向計算的最小二乘算法參數(shù)辨識精對準(zhǔn)模型如下：

系統(tǒng)狀態(tài)變量為

(9)

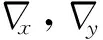
系統(tǒng)量測方程為

Z=HX+V

(10)

其中

(11)

式中V為量測噪聲矢量。

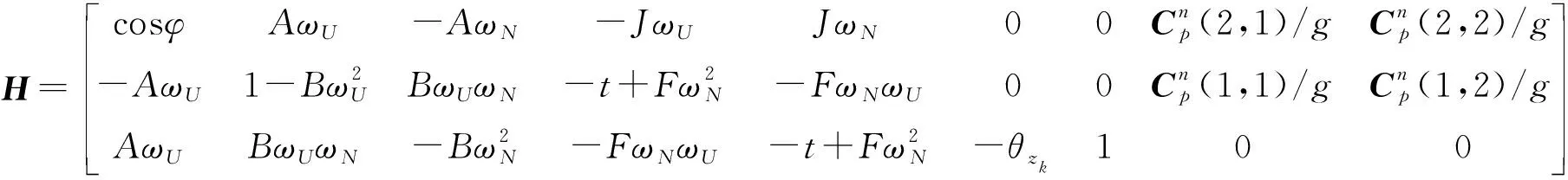
(12)

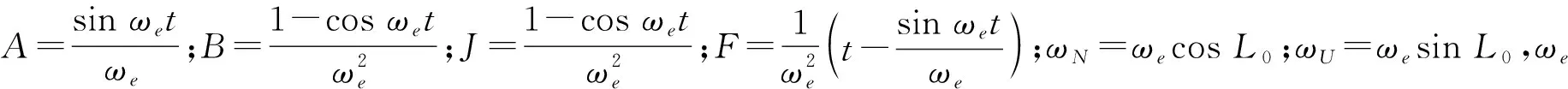
(13)

(14)

(15)

(16)

1.5.1參數(shù)辨識精對準(zhǔn)中正向?qū)Ш浇馑闼惴?/p>

正向?qū)Ш浇馑氵^程中,式(11)中的fE、fN可由下式計算獲得：

(17)

(18)

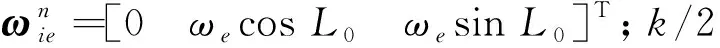
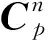
(19)

tanψ=T′12/T′22

(20)

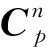
(21)

正向?qū)Ш浇馑氵^程中H陣中的θzk-1為

θzk=θzk-1+Δθz

(22)

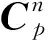
估計參數(shù)的遞推最小二乘方程為

Hk+1Pk

(23)

(24)

式中，對準(zhǔn)開始時刻k=0時，X0=0；P0=1 000I，依據(jù)遞推最小二乘公式即可估計出誤差參數(shù)X。

1.5.2參數(shù)辨識精對準(zhǔn)中逆向?qū)Ш浇馑闼惴?/p>

逆向?qū)Ш浇馑氵^程中,量測量Z中fE、fN可由下式計算得到，即

(25)

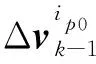
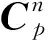
(26)

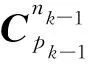
逆向?qū)Ш浇馑氵^程中，H陣中θzk-1為

θzk-1=θzk-Δθz

(27)

式中Δθz可由粗對準(zhǔn)過程中存儲的關(guān)鍵數(shù)據(jù)獲得。

逆向遞推最小二乘方程為

Hk-1Pk

(28)

(29)

式中對準(zhǔn)開始時刻k=0時對應(yīng)的X和P陣,X0和P0取正向最小二乘方程中末時刻的狀態(tài)變量和系統(tǒng)狀態(tài)方差陣，依據(jù)逆向遞推最小二乘公式即可估計出誤差參數(shù)X。

2 試驗驗證

為了進一步驗證本文提出的基于時間正逆向計算對準(zhǔn)算法靜基座時在實際慣導(dǎo)系統(tǒng)中的對準(zhǔn)效果，本節(jié)利用一套實際單軸光纖陀螺慣導(dǎo)系統(tǒng)進行靜基座對準(zhǔn)跑車試驗。試驗中，車輛先靜止一段時間進行對準(zhǔn)，對準(zhǔn)后車輛可自由行進。粗對準(zhǔn)結(jié)束后，利用粗對準(zhǔn)過程中保存的數(shù)據(jù)進行基于時間正逆向計算的參數(shù)辨識精對準(zhǔn)算法。由于跑車試驗中無法提供姿態(tài)基準(zhǔn)，本實驗以導(dǎo)航位置誤差來驗證精對準(zhǔn)精度。試驗中對準(zhǔn)時間為16 min，其中傳統(tǒng)對準(zhǔn)算法中，粗對準(zhǔn)4 min，精對準(zhǔn)12 min，基于時間正逆向計算的對準(zhǔn)算法中，粗對準(zhǔn)12 min，精對準(zhǔn)利用粗對準(zhǔn)過程中保存的12 min數(shù)據(jù)進行第一次正、逆向計算，再利用保存的全部16 min數(shù)據(jù)進行第二次正向精對準(zhǔn)。試驗過程中載體的速度及姿態(tài)曲線如圖2、3所示。傳統(tǒng)對準(zhǔn)算法和基于正逆向計算算法中平臺偏角的收斂曲線如圖4、5所示。z陀螺漂移的收斂曲線如圖6所示。其位置誤差(ΔSN,ΔSZ)對比曲線如圖7所示。圖7中位置基準(zhǔn)以GPS提供的位置，誤差曲線為慣導(dǎo)與GPS的位置差。

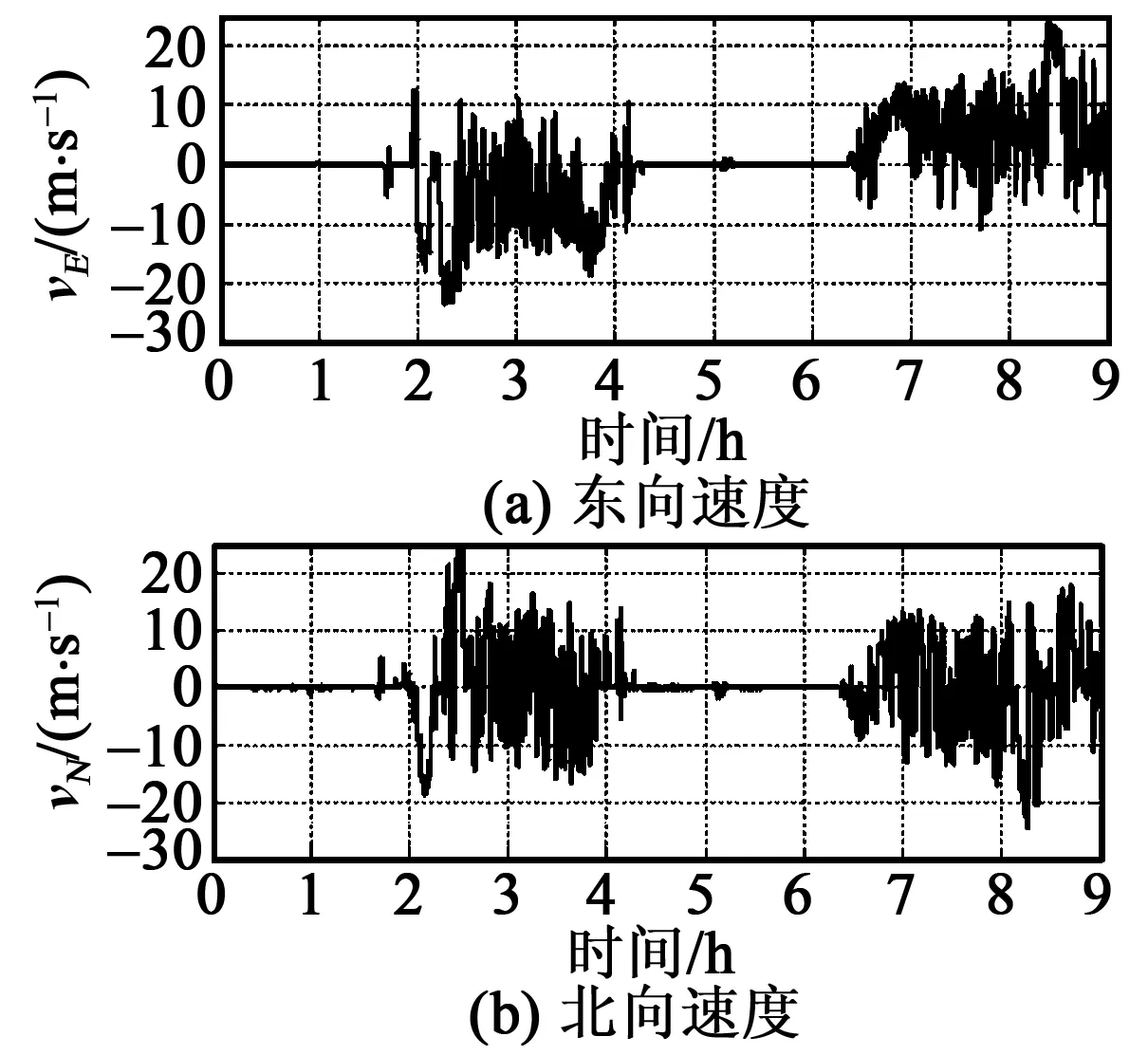
圖2 載體東北向速度

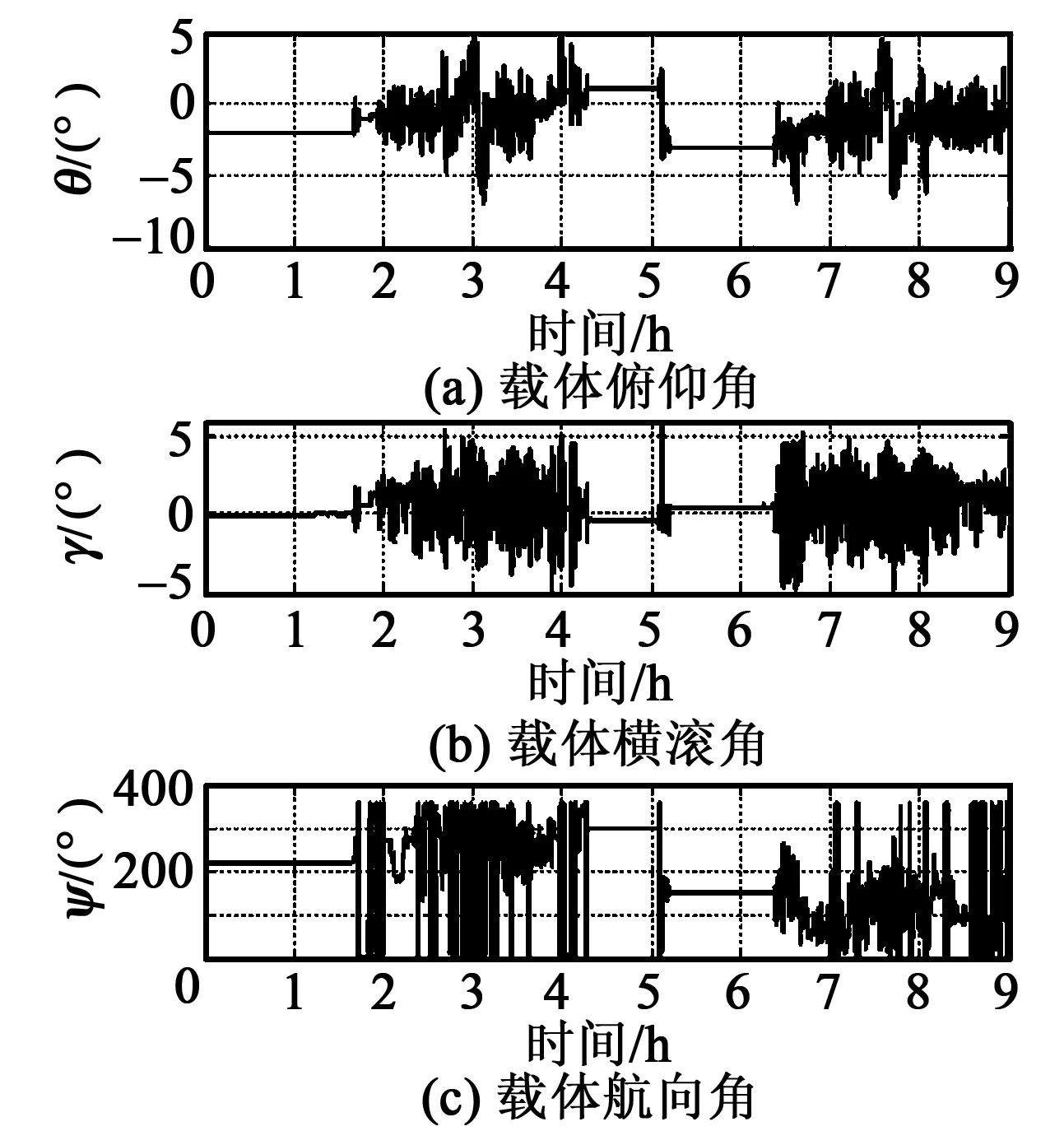
圖3 載體姿態(tài)

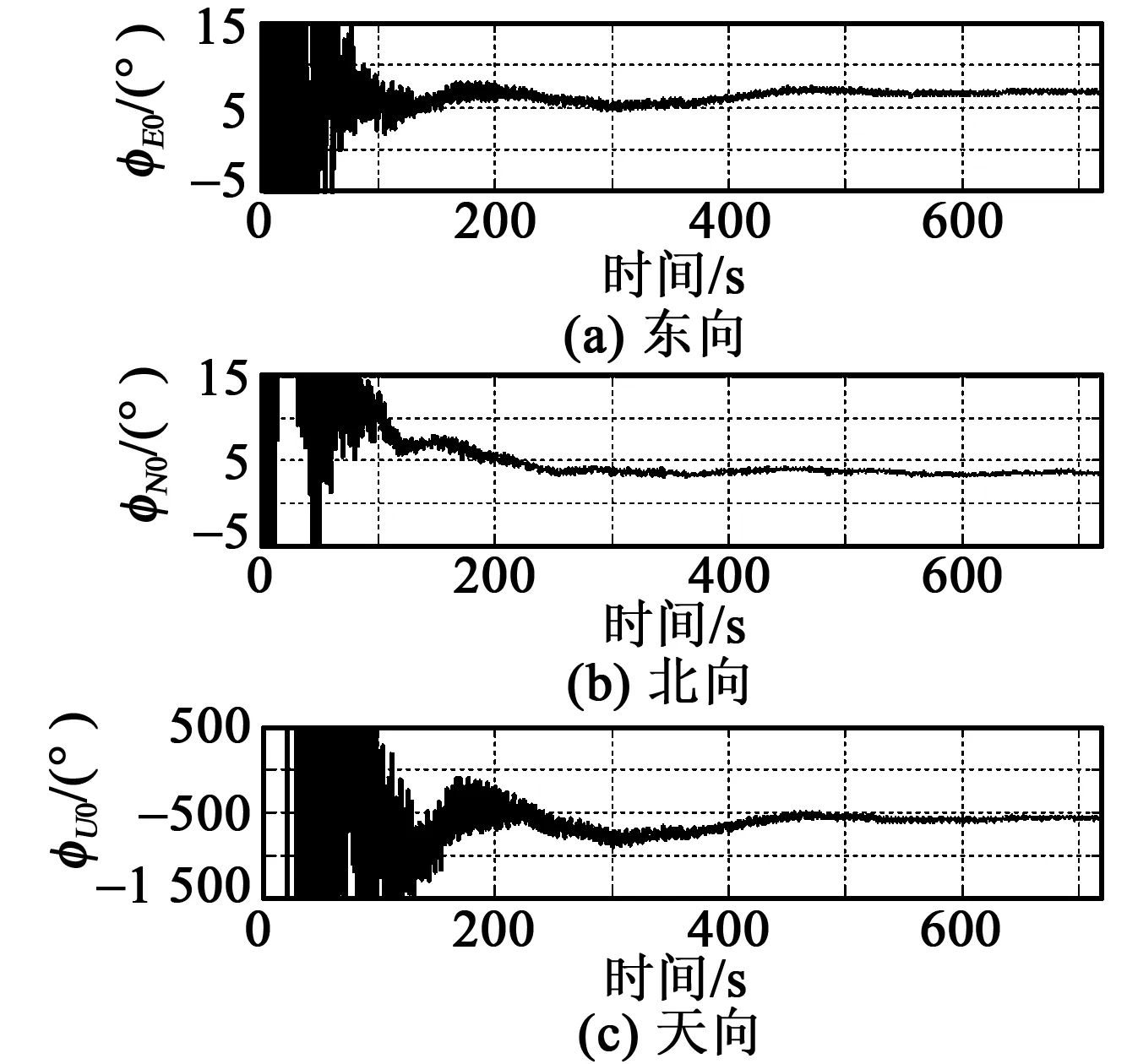
圖4 傳統(tǒng)對準(zhǔn)算法中平臺偏角收斂曲線

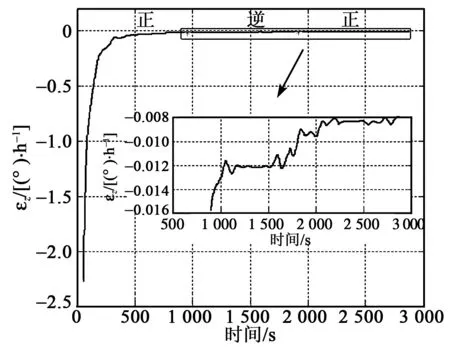
圖6 z軸陀螺漂移估計結(jié)果

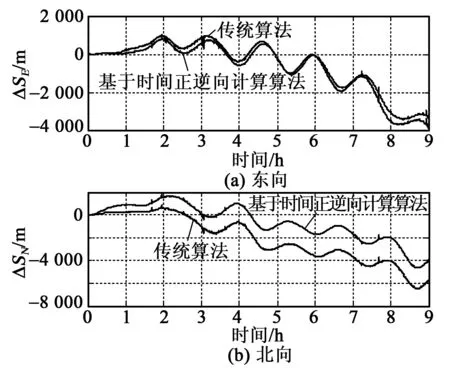
圖7 跑車試驗東北向位置誤差對比

由圖2可以看出，載體跑車過程中東、北向的速度最大、最小值達到了±20 m/s。由圖3可以看出，載體跑車過程中有轉(zhuǎn)彎運動也有掉頭運動。在圖2、3所示的運動狀態(tài)下，利用圖4、5可以看出，本文提出的對準(zhǔn)方法相當(dāng)于變相延長了對準(zhǔn)時間，且能很快估計出z軸陀螺漂移(見圖6)，z軸陀螺漂移收斂至-0.008 (°)/h。經(jīng)過對準(zhǔn)并補償z軸陀螺漂移后，經(jīng)過9 h的導(dǎo)航結(jié)果如圖7所示，由圖7可以看出，基于時間正逆向計算后,9 h定位誤差東向最大值為3 370 m，北向最大誤差為4 631 m，而基于傳統(tǒng)算法9 h定位誤差東向最大值為3 875 m，北向最大誤差為6 446 m，因此,利用本文提供方法使系統(tǒng)的徑向定位誤差從7 521.1 m減小為5 727.4 m，定位精度提高約24%。從跑車試驗結(jié)果證明基于時間正逆向計算的方法定位誤差更小，定位精度優(yōu)于2 n mile/12 h，對準(zhǔn)方法更優(yōu)。

3 結(jié)束語

本文提出的基于數(shù)據(jù)存儲的正逆向計算快速對準(zhǔn)方法，首先利用實時采集的陀螺和加速度計數(shù)據(jù)進行基于慣性系初始姿態(tài)的粗對準(zhǔn)，在實時粗對準(zhǔn)過程中，同步壓縮每秒的陀螺加速度計信息并將其存儲；然后利用存儲數(shù)據(jù)再進一步執(zhí)行基于時間正逆向計算的精對準(zhǔn)。從實際系統(tǒng)的跑車結(jié)果可驗證，經(jīng)過對準(zhǔn)及z軸陀螺漂移誤差補償后，系統(tǒng)定位精度提高了約24%，定位誤差小于2 n mile/12 h。