基于二分搜索改進Karnik-Mendel算法的廣義二型模糊邏輯系統降型*

陳 陽，王 濤

(遼寧工業大學理學院,遼寧 錦州 121001)

1 引言

作為一種新興技術，區間二型模糊邏輯系統[1 - 5]已被成功應用在許多有較高不確定性和非線性特征的領域。盡管如此，自從廣義二型模糊集的α-平面(或稱z切片)表達理論[6-9]被幾個不同的研究小組提出后，學術界許多關注從區間二型模糊邏輯系統轉向了廣義二型模糊邏輯系統。由于廣義二型模糊邏輯系統計算復雜度被顯著降低，這使得它們在近幾年逐漸被應用在如邊緣檢測[10]、模糊控制[11]和預測[12]等具有較強不確定性領域。廣義二型模糊集的次隸屬度介于0～1，所以它們可看成比區間二型模糊集更高階的模糊集參數模型。隨著設計自由度增加，廣義二型模糊邏輯系統在處理某些不確定性問題上比區間二型模糊邏輯系統更有潛力。

廣義二型模糊邏輯系統一般由模糊器、規則庫、推理機、降型器和解模糊器5個模塊構成，如圖1所示[9]。降型是系統的核心模塊，它把二型模糊集映射成一型模糊集，而解模糊化又把一型模糊集變成明確輸出值。當前最流行的改進Karnik-Mendel EKM(Enhanced Karnik-Mendel)算法具有保持不確定性在上級和下級隸屬函數之間流動的優勢。盡管如此，這類算法計算很密集。Liu等人[13,14]給出了EKM算法初始化理論解釋，并擴展EKM算法為3種不同加權形式的加權EKM WEKM(Weighted EKM)算法計算區間二型模糊集質心。為了提高計算效率，邢海花等人[15]提出了一種二分搜索改進Karnik-Mendel BEKM(Binary-search EKM)算法計算區間二型模糊集質心。這些工作為研究廣義二型模糊邏輯系統質心降型奠定了一定的基礎。

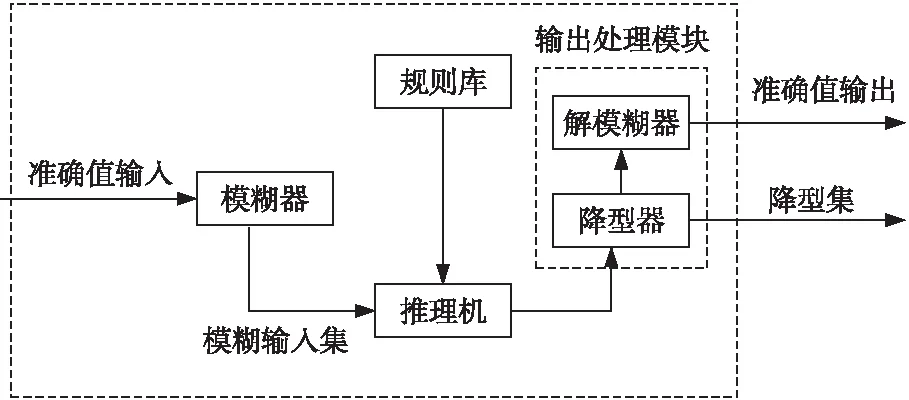
Figure 1 A general type-2 fuzzy logic system圖1 一個廣義二型模糊邏輯系統

基于廣義二型模糊集的α-平面表達理論，本文討論了廣義二型模糊邏輯系統的模糊推理、降型和解模糊化等模塊，并提出用BEKM算法完成廣義二型模糊邏輯系統質心降型。通過2個計算機仿真示例闡述了BEKM算法相對于EKM算法的表現，當計算系統質心降型集右端點時，BEKM算法在不損失計算精度的前提下明顯快于EKM算法。

2 廣義二型模糊邏輯系統

從推理角度考慮，廣義二型模糊邏輯系統可分為Mamdani型[16]和TSK(Takagi-Sugeno-Kang)型[11,17]。這里研究Mamdani型廣義二型模糊邏輯系統降型。不失一般性，考慮一個有n個輸入x1∈X1,…,xn∈Xn和一個輸出y∈Y的廣義二型模糊邏輯系統。 該系統可由M條模糊規則描述，其中第s條規則的形式為：

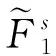
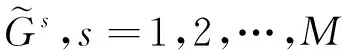
(1)

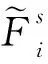
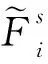
(2)

對于每條模糊規則，其在特定的α水平下的激發區間為：

(3)

其中,p為前件數，T表示乘積t-范數或取小t-范數。

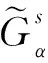
(4)

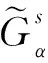
(5)

(6)

(7)

(8)

(9)

聚合所有的YC,α得出最終的一型降型集YC,即:

(10)

設α-平面的個數為m,即把α均勻分解成α1,α2,…,αm,則廣義二型模糊邏輯系統輸出為:

(11)

3 BEKM算法

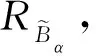
(12)

(13)

其中，k和k′表示切換點。

相比于最初的KM算法，EKM算法改進了以下3個方面：

(1) 提出了更好的初始化方法；(2) 去掉一步不必要的迭代來改變迭代終止條件；(3) 設置巧妙的計算方法以減少算法每次迭代的計算消耗。

盡管如此，EKM算法仍然計算密集。BEKM算法又在以下2方面改進了EKM算法：

(1) BEKM算法設置初始化切換點為k=[N/2],這種設置會適合任意類型的二型模糊集。EKM算法設置初始化左右切換點分別為k=[N/2.4]和k′=[N/1.7],這導致當真正的切換點遠離初始化切換點時，EKM算法的計算效率大幅降低。

(2) EKM算法在每次迭代中都從1開始向上至N-1搜索切換點k′,而BEKM算法在每次迭代中都縮減[N/2]的范圍，因此，后者的計算效率更高。

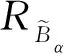
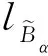
(1)把主變量均勻離散成N個點，即yi(i=1,2,…,N)。

(2)初始化：設置kmax=N,kmin=1,且k=(kmax+kmin)/2。

(5)如果yk>y，則設置kmax=k-1且轉入步驟(7)；否則，進入步驟(6)。

(6)如果yk+1≤y，則設置kmin=k+1且轉入步驟(7)。

(8)設置y=y′,a=a′,b=b′，且返回步驟(4)。

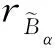
(1) 把主變量均勻離散成N個點，即yi(i=1,2,…,N)。

(2)初始化：設置kmax=N,kmin=1,且k=(kmax+kmin)/2。

(5)如果yk>y，則設置kmax=k-1且轉入步驟(7)；否則，進入步驟(6)。

(6)如果yk+1≤y，則設置kmin=k+1且轉入步驟(7)。

(8) 設置y=y′,a=a′,b=b′且返回步驟(4)。

最后介紹如何用BEKM算法完成基于廣義二型模糊集α-平面表達理論廣義二型模糊邏輯系統質心降型，其具體的計算步驟如下所示：

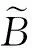
(3) 根據仿真實驗結果，比較和分析2種算法的表現。

4 仿真實驗

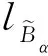
圖2和表1給出了所定義的2個示例的FOU。圖3和表2又提供了所定義的相關次隸屬函數。

Figure 2 Graphs of FOU圖2 FOU圖

Table 1 FOU membership function expressions for two examples表1 2個示例FOU隸屬函數表達式

Figure 3 Shape graphs of secondary membership functions圖3 次隸屬函數形狀圖

Table 2 Secondary membership function expressions for two examples表2 2個示例的次隸屬函數表達式

Figure 4 The right half centroid type-reduced sets computed by the EKM algorithm and BEKM algorithm圖4 EKM算法和BEKM算法計算出的右半質心降型集

當取有效α-平面個數Δ=100時，用EKM算法和BEKM算法計算出2個示例的右半質心降型集如圖4所示。

接著研究2種算法計算右半質心降型集的具體的計算時間，其計算結果是不可重復的。取仿真平臺為E5300@2.60 GHz和2.00 GB內存的雙核CPU的戴爾臺式機，Microsoft Windows XP Professional操作系統。所有程序在Matlab 2013a中運行，2個示例的總計算時間如表3所示，其中第4行表示計算結果平均值，而第4列表示BEKM算法相對于EKM算法的計算時間減少率，這里把它定義為：

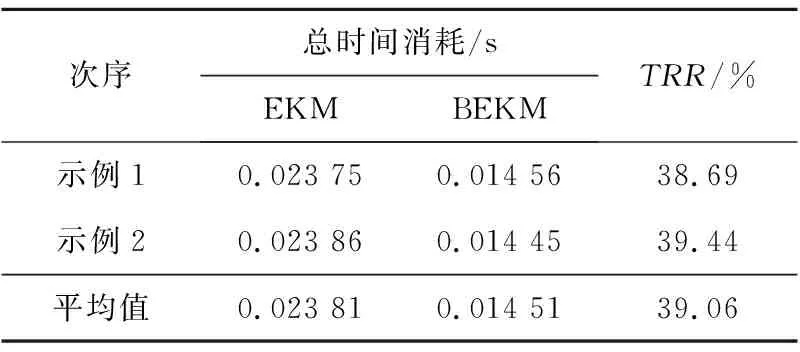
Table 3 Total time consuming of two algorithms for computing the right half centroid type-reduced sets表3 2種算法計算右半質心降型集總時間消耗

TRR=(tEKM-tBEKM)/tEKM×100%

(14)

其中,tEKM為EKM算法計算時間，tBEKM為BEKM算法計算時間，時間單位為s。

仔細觀察圖3和表3，當計算廣義二型模糊邏輯系統右半質心降型集時，可以得到以下結論：

(1) 在以上2個最常見的示例中，EKM算法和BEKM算法計算右半質心降型集的結果幾乎完全相同，如圖3a和圖3b所示，代表2種算法的曲線幾乎完全重合；

(2) 相比于EKM算法，所提出的BEKM算法在2個示例中分別減少了約39.69%和39.44%的計算時間，此外，相對EKM算法，BEKM算法的平均計算時間減少率為39.06%。

以上的仿真實驗分析表明，本文提出的BEKM算法是完成廣義二型模糊邏輯系統質心降型的一種有效方法。盡管EKM算法和BEKM算法計算出的廣義二型模糊邏輯系統右半質心降型集結果值幾乎完全相同，但可明顯看出，BEKM算法的計算時間優于EKM算法的。換句話說，所提出的BEKM算法可顯著地改進完成廣義二型模糊邏輯系統質心降型時的計算效率而不損失計算精度。

5 結束語

針對通過廣義二型模糊邏輯系統模糊推理得出的具有不同足跡不確定性和相關次隸屬函數的輸出廣義二型模糊集，本文提出BEKM算法來完成廣義二型模糊邏輯系統質心降型。當計算右半質心降型集時，2個仿真示例表明了盡管2種算法的計算結果幾乎完全相同，但BEKM算法的計算時間遠少于EKM算法的，這可能會給廣義二型模糊邏輯系統設計提供潛在的價值。

接下來將研究EKM算法的初始化，力爭給出合理初始化EKM完成區間二型和廣義二型模糊邏輯系統質心降型。此外，也將深入研究二型模糊邏輯系統的中心集降型[23]、各種離散降型算法和連續降型算法之間的關系[24]以及基于智能優化算法[3 - 5,11,12,16,17,25,26]的二型模糊邏輯系統的設計與應用等。