局部廣義多粒度粗糙集*

王 虹，李敏贏

(山西師范大學數學與計算機科學學院,山西 臨汾 041004)

1 引言

粗糙集理論是由Pawlak[1,2]在1982年提出的，它是處理不精確、不確定、模糊的有效工具。該理論已廣泛應用于數據挖掘、特征選擇、粒計算等領域。經典粗糙集理論是基于單粒即僅有一個等價關系,而多粒度粗糙集是與多個粒結構有關,即具有多個等價關系。多粒度粗糙集是由Qian等[3]在2006年首次提出的，是粗糙集理論的一個重要研究方向，并已成功地應用在許多方面，如多源信息系統、多尺度信息系統等[4]。近幾年來已經被許多學者關注并廣泛研究。Qian等[5]研究了局部多粒度決策論粗糙集，Wang等[6]提出了局部領域粗糙集。 文獻[7]在多粒度粗糙集的基礎上提出了廣義多粒度粗糙集與最優粒選擇。文獻[8-10]提出了多粒度粗糙集模型，分為樂觀多粒度粗糙集和悲觀多粒度粗糙集。Liu[11]提出了變精度粗糙集的矩陣方法。Yao等[12]研究了多粒空間的4種粗糙集模型并提出了一個統一框架來分類和比較現有的研究結果。 Qian等[13]用局部粗糙集解決大數據中粗糙數據分析。汪小燕等[14]研究了基于矩陣的多粒度粗糙集上、下近似表示。劉鳳玲等[15]提出了局部鄰域多粒度粗糙集模型。以上模型依然存在不足，如廣義多粒度粗糙集處理海量數據比較耗時，局部多粒度粗糙集模型中樂觀和悲觀模型過于嚴格或過于寬松，具有一定的局限性。

本文將在這些研究的基礎上，研究局部廣義多粒度粗糙集模型，同時提出一種用矩陣求解局部廣義多粒度粗糙集上下近似的方法，既考慮了少數服從多數的情況，又節省了時間。

2 預備知識

2.1 廣義多粒度粗糙集的上下近似

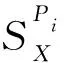
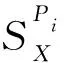
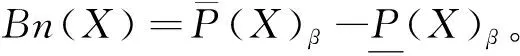
2.2 局部多粒度粗糙集

定義3[5]設R1,R2,…,Rm?R是U上的m個等價關系，?X?U,局部多粒度粗糙集上下近似定義為：

{x|P(X|[x]R1)≥α∨P(X|[x]R2)≥

α∨…∨P(X|[x]Rm)≥α}

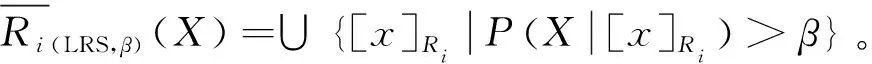
邊界域或者不確定性區域的定義為：

2.3 關系矩陣[11]

設U={x1,x2,…,xn}是有限對象集，R是U上的二元關系，定義rR(x)={y|y∈U,xRy}。如果?x∈U,rR(x)≠?，則R是串行的。

如果?X?U,?x∈U,定義X的特征函數λX為：

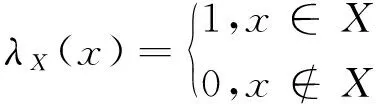
定義4對于U上串行的關系R,假設MR=(aij)n×n是R的關系矩陣，即aij=λR(xi,xj)。定義n×n矩陣:

WR=NRMR=

設R是U上串行的關系。?X?U,則：

其中T表示轉置。

3 局部廣義多粒度粗糙集模型

3.1 局部廣義多粒度粗糙集的上下近似

對于未標記數據，即在決策屬性下只能有限數據帶標記，當求廣義多粒度粗糙集下近似和上近似時需要所有對象的等價類，包括標記對象和未標記對象，而局部廣義多粒度粗糙集上近似用等價類的并表示，即某些對象的等價類里包含未標記的對象，只需要計算目標概念X的對象，因此可用帶標記的有限數據集充分發現未標記數據集隱藏的信息，同時也節約了大量時間。

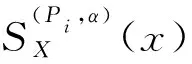
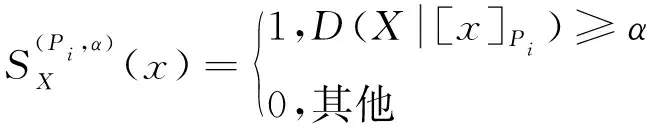
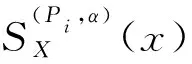
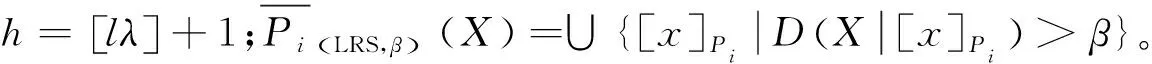
3.2 局部廣義多粒度粗糙集上下近似的矩陣表示

定義6設I=(U,A,V,f)是信息系統，設U={x1,x2,…,xn},X?U,P={P1,P2,…,Pl},Pi?A(i=1,2,…,l)，設關于X的特征函數為:

記對角矩陣:

和對象多粒關系矩陣:

其中,aij=Ri(x,xj);i=1,2,…,l;j=1,2,…,n。根據矩陣的乘法得:

WR(x)=NR(x)M(x)=

μ(x)=WR(x)λX(x)=

設X={xi1,xi2,…,xis},(μ(x))α是μ(x)的α截集，則有I=E1×n(μ(x))α=(l1,l2,…,ls),(μ(x))α=(μ(xi1),μ(xi2),…,μ(xis))α。

定義7設I=(U,A,V,f)是信息系統，X?U,P={P1,P2,…,Pl},Pi?A(i=1,2,…,l),稱(μ(x))α是關于X多粒度粗糙集布爾矩陣。

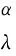
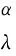
定義9設I=(U,A,V,f)是信息系統，X?U,P={P1,P2,…,Pl},Pi?A(i=1,2,…,l),關于X多粒度粗糙集矩陣Bβ(X)=(bij)定義為：

多粒度粗糙集矩陣包含|X|行、l列，其中|X|表示X中元素的個數，l表示粒度個數，多粒度粗糙集矩陣的非空元素由等價類或者?組成。

關于X多粒度粗糙集矩陣表示為:

記:

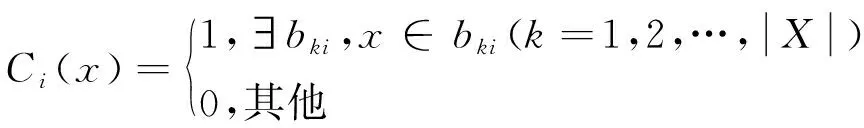
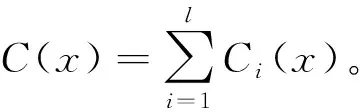
定義10設I=(U,A,V,f)是信息系統，X?U,P={P1,P2,…,Pl},Pi?A(i=1,2,…,l),局部廣義多粒度粗糙集上近似為:

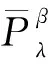
其中,lλ是整數時，h=lλ;當lλ是分數時，h=[lλ]+1。

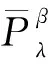
引理1[7]?a1,a2,b1,b2∈[0,1],下列不等式成立：

(1)a1∧b1+a2∧b2≤(a1+a2)∧(b1+b2);

(2)a1∨b1+a2∨b2≤(a1+a2)∨(b1+b2)。

定理1設I=(U,A,V,f)是信息系統，X,Y?U,P={P1,P2,…,Pl},Pi?A(i=1,2,…,l)。?λ∈(0,1],當α>β時,下列性質成立：

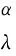
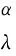
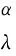
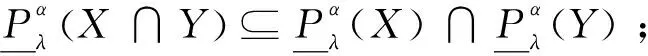
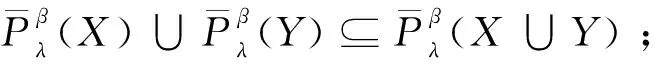
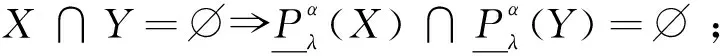
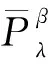
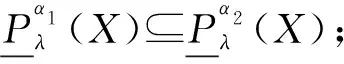
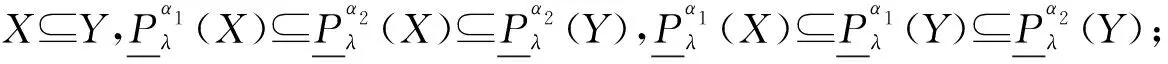
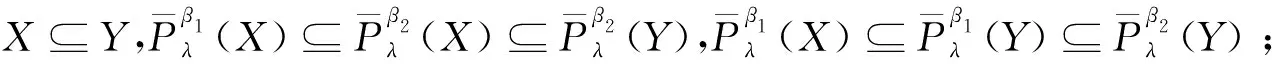
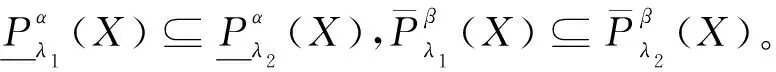
證明(1)和(2)可直接由局部廣義多粒度粗糙集的上下近似得到。

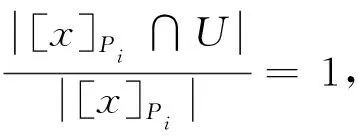
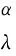
而

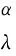
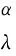
由引理1可得:

(7)、(8)的證明與(5)、(6)的類似。

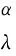
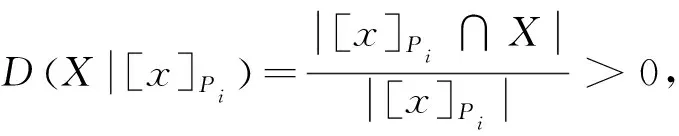
(12)的證明與(11)的類似。

(14) 由(4)和(12)直接得證。

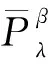
定理2設I=(U,A,V,f)是信息系統，X?U,P={P1,P2,…,Pl},Pi?A(i=1,2,…,l)。?λ∈(0,1],當α>β時,局部廣義多粒度粗糙集的上下近似與樂觀多粒度粗糙集和悲觀多粒度粗糙集有下列性質成立：

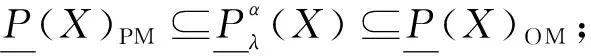
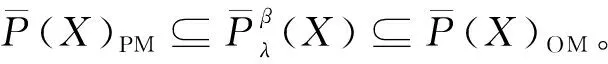
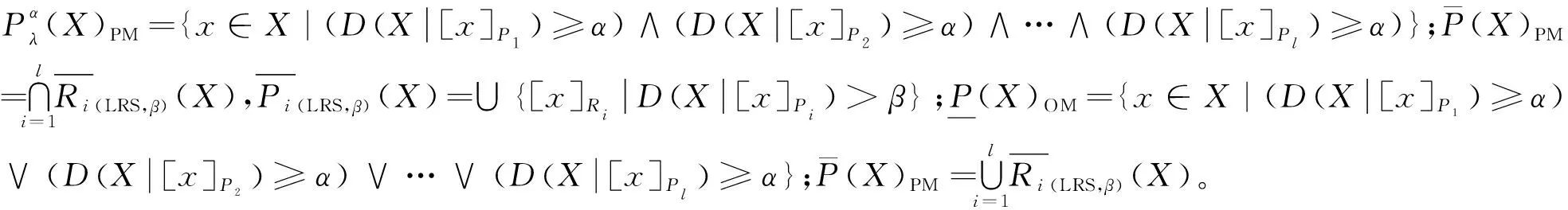
(2)的證明與(1)的類似。

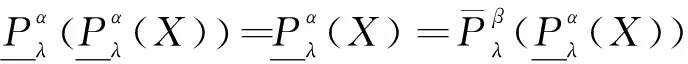
例1表1是一個信息系統，假設P={P1,P2,P3},α=0.6,β=0.4,λ=0.7,X1={x1,x2,x3,x4,x7},X2={x1,x2,x3,x4,x7,x8}。

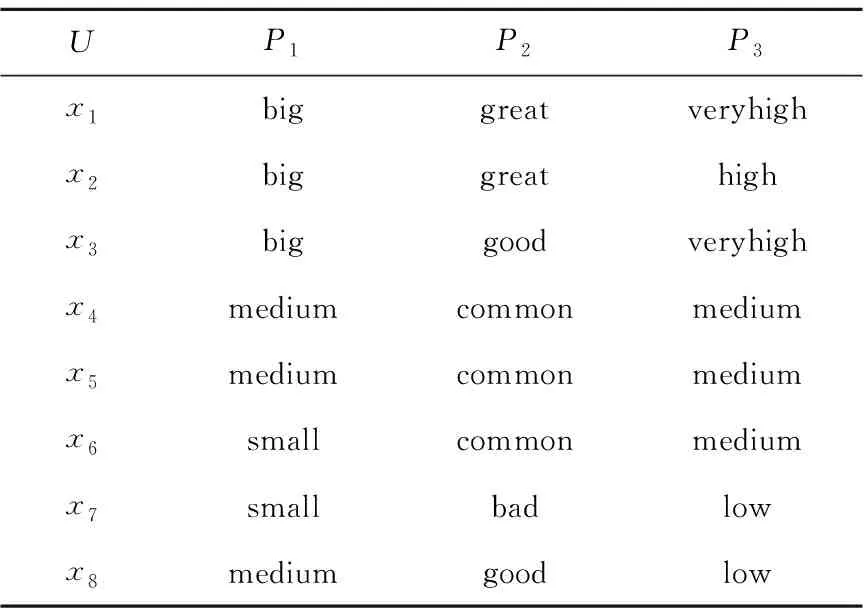
Table 1 Information system 1表1 信息系統1

為了計算局部廣義多粒度粗糙集的下近似，只需要計算來自集合X1中對象的等價類，經計算可得：

[x1]P1={x1,x2,x3},[x2]P1={x1,x2,x3},[x3]P1={x1,x2,x3},[x4]P1={x4,x5,x8},[x7]P1={x6,x7}。

[x1]P2={x1,x2},[x2]P2={x1,x2},[x3]P2={x3,x8},[x4]P2={x4,x5,x6},[x7]P2={x7}。

[x1]P3={x1,x3},[x2]P3={x2},[x3]P3={x1,x3},[x4]P3={x4,x5,x6},[x7]P3={x7,x8}。

D(X1|[x1]P1)=1,D(X1|[x2]P1)=1,D(X1|[x3]P1)=1,D(X1|[x4]P1)=1/3,D(X1|[x7]P1)=1/2,D(X1|[x1]P2)=1,D(X1|[x2]P2)=1,D(X1|[x3]P2)=1/2,D(X1|[x4]P2)=1/3,D(X1|[x7]P2)=1,D(X1|[x1]P3)=1,D(X1|[x2]P3)=1,D(X1|[x3]P3)=1,D(X1|[x4]P3)=1/3,D(X1|[x7]P3)=1/2。

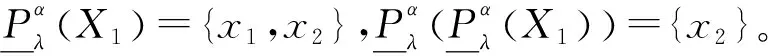
當β=0.4,λ=0.7時,經計算可得矩陣:

綜上注1一般不成立。

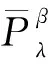
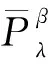
例2表2是一個信息系統，假設P={P1,P2,P3,P4},其中P1={a,b},P2={c,d},P3={e,f},P4={g},α=0.6,β=0.4,λ=0.6,X={x1,x2,x4,x5,x8,x9,x16}。

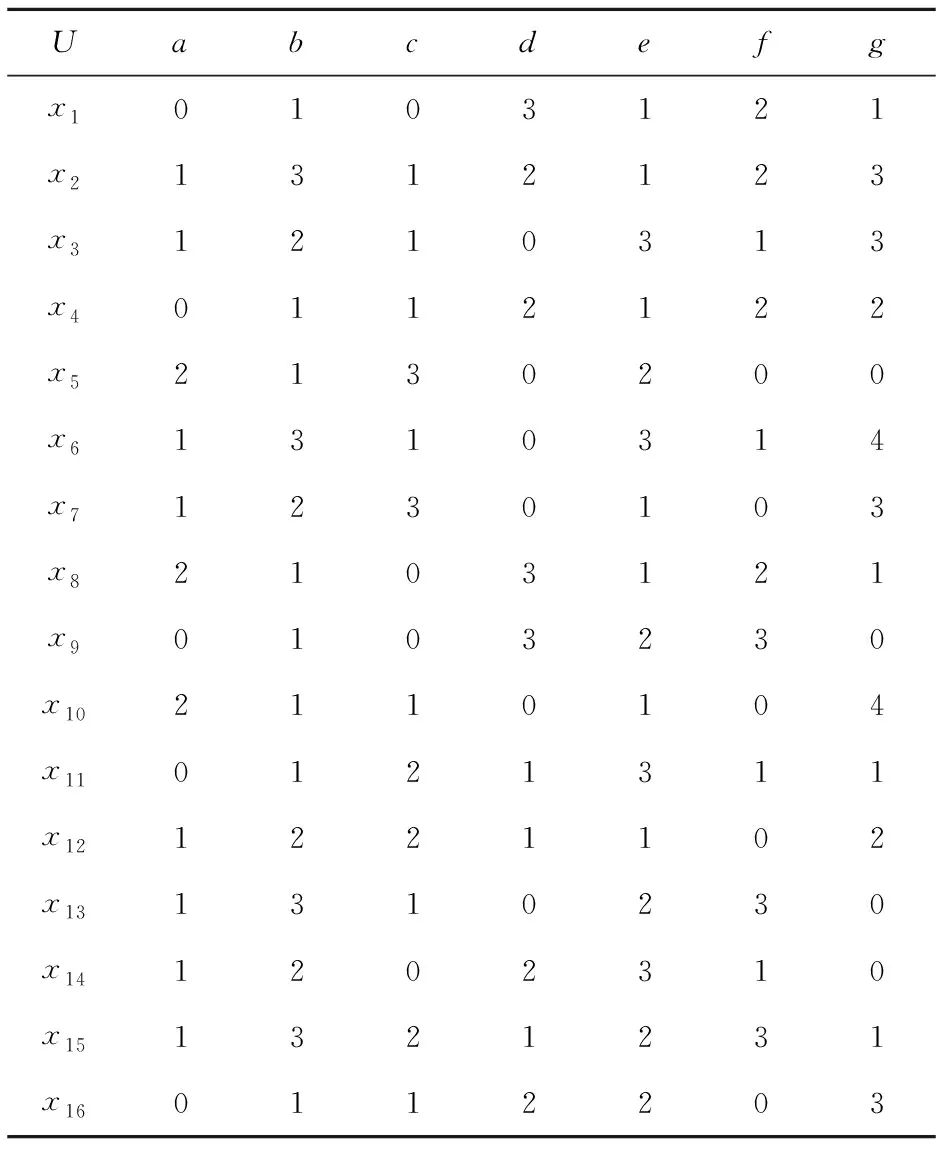
Table 2 Information system 2表2 信息系統2

為了計算局部廣義多粒度粗糙集的下近似，只需要計算來自集合X中對象的等價類，經計算可得：

[x1]P1={x1,x4,x9,x11,x16},[x2]P1={x2,x6,x13,x15},[x4]P1={x2,x6,x13,x15},[x5]P1={x5,x8,x10},[x8]P1={x5,x8,x10},[x9]P1={x1,x4,x9,x11,x16},[x16]P1={x1,x4,x9,x11,x16}。

[x1]P2={x1,x8,x9},[x2]P2={x2,x4,x16},[x4]P2={x2,x4,x16},[x5]P2={x5,x7},[x8]P2={x1,x8,x9},[x9]P2={x1,x8,x9},[x16]P2={x2,x4,x16}。

[x1]P3={x1,x2,x4,x8},[x2]P3={x1,x2,x4,x8},[x4]P3={x1,x2,x4,x8},[x5]P3={x5,x16},[x8]P3={x1,x2,x4,x8},[x9]P3={x9,x13,x15},[x16]P3={x5,x16}。

[x1]P4={x1,x8,x11,x15},[x2]P4={x2,x3,x7,x16},[x4]P4={x4,x12},[x5]P4={x5,x9,x13,x14},[x8]P4={x1,x8,x11,x15},[x9]P4={x5,x9,x13,x14},[x16]P4={x2,x3,x7,x16}。

D(X|[x1]P1)=4/5,D(X|[x2]P1)=1/4,D(X|[x4]P1)=4/5,D(X|[x5]P1)=2/3,D(X|[x8]P1)=2/3,D(X|[x9]P1)=4/5,D(X|[x16]P1)=4/5。

D(X|[x1]P2)=1,D(X|[x2]P2)=1,D(X|[x4]P2)=1,D(X|[x5]P2)=1/2,D(X|[x8]P2)=1,D(X|[x9]P2)=1,D(X|[x16]P2)=1。

D(X|[x1]P3)=1,D(X|[x2]P3)=1,D(X|[x4]P3)=1,D(X|[x5]P3)=1/2,D(X|[x8]P3)=1,D(X|[x9]P3)=1/3,D(X|[x16]P3)=1。

D(X|[x1]P4)=1/2,D(X|[x2]P4)=1/2,D(X|[x4]P4)=1/2,D(X|[x5]P4)=1/2,D(X|[x8]P4)=1/2,D(X|[x9]P4)=1/2,D(X|[x16]P4)=1/2。

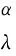
當β=0.4,λ=0.6時,經計算可得矩陣Bβ(X)。

Bβ(X)=[B1B2]

為了計算廣義多粒度粗糙集的下近似，只需要計算來自集合U中對象的等價類，經計算可得：

[x1]P1={x1,x4,x9,x11,x16},[x2]P1={x2,x6,x13,x15},[x3]P1={x3,x7,x12,x14},[x4]P1={x2,x6,x13,x15},[x5]P1={x5,x8,x10},[x6]P1={x2,x6,x13,x15},[x7]P1={x3,x7,x12,x14},[x8]P1={x5,x8,x10},[x9]P1={x1,x4,x9,x11,x16},[x10]P1={x5,x8,x10},[x11]P1={x1,x4,x9,x11,x16},[x12]P1={x3,x7,x12,x14},[x13]P1={x2,x6,x13,x15},[x14]P1={x3,x7,x12,x14},[x15]P1={x2,x6,x13,x15},[x16]P1={x1,x4,x9,x11,x16}。

[x1]P2={x1,x8,x9},[x2]P2={x2,x4,x16},[x3]P2={x3,x6,x10,x13},[x4]P2={x2,x4,x16},[x5]P2={x5,x7},[x6]P2={x3,x6,x10,x13},[x7]P2={x5,x7},[x8]P2={x1,x8,x9},[x9]P2={x1,x8,x9},[x10]P2={x3,x6,x10,x13},[x11]P2={x11,x12,x15},[x12]P2={x11,x12,x15},[x13]P2={x3,x6,x10,x13},[x14]P2={x14},[x15]P2={x11,x12,x15},[x16]P2={x2,x4,x16}。

[x1]P3={x1,x2,x4,x8},[x2]P3={x1,x2,x4,x8},[x3]P3={x3,x6,x11,x14},[x4]P3={x1,x2,x4,x8},[x5]P3={x5,x16},[x6]P3={x3,x6,x11,x14},[x7]P3={x7,x10,x12},[x8]P3={x1,x2,x4,x8},[x9]P3={x9,x13,x15},[x10]P3={x7,x10,x12},[x11]P3={x3,x6,x11,x14},[x12]P3={x7,x10,x12},[x13]P3={x9,x13,x15},[x14]P3={x3,x6,x11,x14},[x15]P3={x9,x13,x15},[x16]P3={x5,x16}。

[x1]P4={x1,x8,x11,x15},[x2]P4={x2,x3,x7,x16},[x3]P4={x2,x3,x7,x16},[x4]P4={x4,x12},[x5]P4={x5,x9,x13,x14},[x6]P4={x6,x10},[x7]P4={x2,x3,x7,x16},[x8]P4={x1,x8,x11,x15},[x9]P4={x5,x9,x13,x14},[x10]P4={x6,x10},[x11]P4={x1,x8,x11,x15},[x12]P4={x4,x12},[x13]P4={x5,x9,x13,x14},[x14]P4={x5,x9,x13,x14},[x15]P4={x1,x8,x11,x15},[x16]P4={x2,x3,x7,x16}。

D(X|[x1]P1)=4/5,D(X|[x2]P1)=1/4,D(X|[x3]P1)=0,D(X|[x4]P1)=4/5,D(X|[x5]P1)=2/3,D(X|[x6]P1)=4/5,D(X|[x7]P1)=0,D(X|[x8]P1)=2/3,D(X|[x9]P1)=4/5,D(X|[x10]P1)=2/3,D(X|[x11]P1)=4/5,D(X|[x12]P1)=0,D(X|[x13]P1)=1/4,D(X|[x15]P1)=1/4,D(X|[x16]P1)=4/5。

D(X|[x1]P2)=1,D(X|[x2]P2)=1,D(X|[x3]P2)=0,D(X|[x4]P2)=1,D(X|[x5]P2)=1/2,D(X|[x6]P2)=0,D(X|[x7]P2)=1/2,D(X|[x8]P2)=1,D(X|[x9]P2)=1,D(X|[x10]P2)=0,D(X|[x11]P2)=0,D(X|[x12]P2)=0,D(X|[x13]P2)=0,D(X|[x14]P2)=0,D(X|[x15]P2)=0,D(X|[x16]P2)=1。

D(X|[x1]P3)=1,D(X|[x2]P3)=1,D(X|[x3]P3)=0,D(X|[x4]P3)=1,D(X|[x5]P3)=1/2,D(X|[x6]P3)=0,D(X|[x7]P3)=0,D(X|[x8]P3)=1,D(X|[x9]P3)=1/3,D(X|[x10]P3)=0,D(X|[x11]P3)=0,D(X|[x12]P3)=0,D(X|[x13]P3)=1/3,D(X|[x14]P3)=0,D(X|[x15]P3)=1/3,D(X|[x16]P3)=1。

D(X|[x1]P4)=1/2,D(X|[x2]P4)=1/2,D(X|[x3]P4)=1/2,D(X|[x4]P4)=1/2,D(X|[x5]P4)=1/2,D(X|[x6]P4)=0,D(X|[x7]P4)=1/2,D(X|[x8]P4)=1/2,D(X|[x9]P4)=1/2,D(X|[x10]P4)=0,D(X|[x11]P4)=1/2,D(X|[x12]P4)=1/2,D(X|[x13]P4)=1/2,D(X|[x14]P4)=1/2,D(X|[x15]P4)=1/2,D(X|[x16]P4)=1/2。

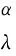
通過例2可得，局部廣義多粒度粗糙集模型在每個粒下只需要計算7個等價類，而廣義多粒度粗糙集模型在每個粒下只需要計算16個等價類，從而節省了大量時間。

算法1計算局部廣義多粒粗糙集下近似的算法

輸入：I=(U,A,V,f)是一個信息系統，粒度空間P={P1,P2,…,Pl},Pi?A(i=1,2,…,l),目標概念X?U,參數α,λ。

輸出：下近似集LL。

步驟1 Fori=1 tol,j=1 to |X|

計算[xj]Pi;

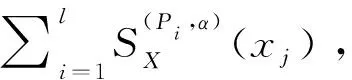
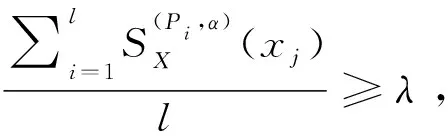
4 結束語

多粒度粗糙集是從多個角度和多個層次進行問題求解的，是經典粗糙集的推廣，已經被大量學者廣泛研究，本文在廣義多粒度粗糙集模型的基礎上進一步提出了局部廣義多粒度粗糙集模型。在此基礎上，給出了一種用矩陣求解局部廣義多粒度粗糙集上下近似的方法，進一步研究了他們的性質。最后，通過一個實例來驗證它的有效性。未來，將研究不同信息系統的局部粗糙集模型。