基于斯坦納樹和泰森多邊形的連通恢復算法*

王茂秋，張 江，張晶,3,4

(1.昆明理工大學信息工程與自動化學院,云南 昆明 650500;2.中國船舶集團有限公司第七〇五研究所昆明分部，云南 昆明 650102;3.云南梟潤科技服務有限公司,云南 昆明 650500;4.昆明理工大學云南省人工智能重點實驗室，云南 昆明 650500)

1 引言

在信息化時代，實時掌握指定區域內狀態的技術常被應用到軍事、氣象等多個領域[1]，作為計算機網絡中最重要的技術，無線傳感器網絡也得到了前所未有的發展。無線傳感器網絡中的傳感器節點通過對覆蓋區域進行數據的收集、信息的檢測、信息的識別、位置的定位和節點的操控來保證對指定區域的信息控制[2]。然而在無線傳感器網絡領域，仍有很多問題需要進一步解決，傳感器節點通常容易因為條件復雜的環境而損壞，再加上節點需要控制自身體積，其所能擁有的能量有限，一旦部分節點損壞或者能量耗盡，會導致正常節點與失效節點無法通信，使得整個傳感器網絡被隔離成若干個獨立的分區，最終導致網絡癱瘓。因此，如何恢復傳感器網絡的連通并且保障恢復后網絡的高效性和健壯性成為了此領域的研究熱點[3]。

近年來，很多學者為無線傳感器網絡連通恢復相關工作做出了努力，Abbasi等人[4]提出了DARA(Distributed Actor Recovery Algorithm)算法，該算法通過綜合距離、節點度和節點標號等因素來選擇現有節點，移動被選節點到指定區域以恢復連通。Senel等人[5,6]將基于蜘蛛網結構的仿生研究應用到無線傳感器網絡連通恢復上，提出了1C-SpiderWeb算法，利用近似網狀的拓撲結構對癱瘓區域實現了連通恢復，但是所需要的中繼節點RN(Relay Node)數量較多，增加了恢復連通的成本，并且這種拓撲結構較為復雜，導致其容錯性較差。Lee等人[7]提出了用最小斯坦納樹恢復無線傳感器網絡多個同時故障的算法，算法以斯坦納樹為初始拓撲結構，研究了RN的放置位置，并以RN的放置位置計算出最少的中繼節點數量，通過移動中繼節點來達到故障區域的連通恢復，但是該算法不能保證移動RN冗余以及恢復連通后傳感器網絡的健壯性。Senel等人[8]在2011年提出FeSTA(Federate network Segments via triangular steiner Tree Approximation)算法,將三角形斯坦納樹結構用于網絡的斷連恢復，利用三角形斯坦納樹結構的特點有效地降低了中繼節點部署數量。

為了使連通恢復后的無線傳感器網絡高效且健壯，本文提出了基于斯坦納樹和泰森多邊形的連通恢復算法CRAST(Connectivity Restoration Algorithm based on Steiner tree and Tyson Polygon)。本文采用改進泰森多邊形部署可移動的備用節點。文獻[9]描述了泰森多邊形的性質以及泰森多邊形的常規生成法，提出了相鄰離散點是以泰森多邊形邊對稱的。文獻[10]提出了使用三角剖分算法構建泰森多邊形，該算法生成泰森多邊形的速度較快，并且提出了新的算法迅速分類出鄰近節點，提高了生成泰森多邊形的效率。

2 網絡模型

2.1 問題描述

四邊形斯坦納樹結構部署RN相比于三角形斯坦納樹結構和最小生成樹結構[11]部署RN，可以以較少的RN實現無線傳感器網絡的連通恢復，故本文使用四邊形斯坦納樹結構來部署RN使癱瘓區域實現連通恢復。由于四邊形斯坦納樹的連通恢復方法過度依賴其中的關鍵節點KN(Key Node)，導致一方面這些KN相較其他節點而言需要消耗更多的能量，最終因能量消耗殆盡而停止工作，另一方面惡劣的外界環境極可能會毀壞這些KN，導致網絡的大片區域再次陷入癱瘓狀態。本文針對這個問題，提出了用泰森多邊形的算法在恢復區域內部署KN的備用節點SN(Standby Node)，在KN損壞時能夠通過移動SN及時地使傳感器網絡再次恢復到連通狀態。

2.2 系統模型

將M個離散點隨機部署在區域Ω中，表示區域Ω中的M個節點。一般情況下，能量耗盡和惡劣的外界條件會導致傳感器某些節點失效，從而使網絡在區域Ω中被拆分為多個節點群。我們把節點群內所有節點能夠相互進行通信的節點群稱為分區，將這些分區看作為點，每個分區用Segi表示，i∈[1,n]，故n為劃分的分區數量，如圖1所示，分區與分區之間無法進行通信。

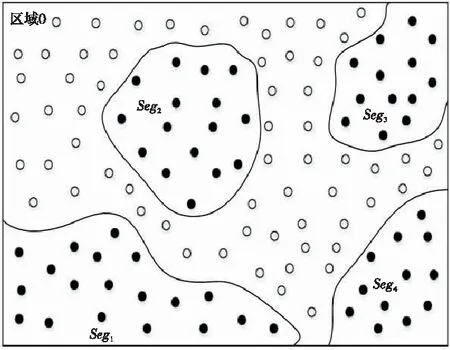
Figure 1 Partitioned area Ω圖1 分區后的區域Ω

2.3 算法基本理論

定義1(四邊形斯坦納點) 根據文獻[12]對于任意1個四邊形，其內部存在2個點，使得四邊形的4個頂點通過這2個點連接的長度最小。

定義2(凸非退化型四邊形) 若1個四邊形中的4個內角均小于或等于120°，則這個四邊形為凸非退化四邊形。

定義3(斯坦納點) 對于任意凸非退化型四邊形ABCD，對其2條對角線的銳角夾角所對的2條邊分別向銳角開口方向作等邊三角形得到△ABE和△BCF,對△ABE和△BCF分別做外接圓；連接E、F得到線段EF，EF與2個外接圓相交的2個點即為ABCD的斯坦納點。

定義4(Delaunay三角網) 由若干個三角形組成的網絡，并且互為相鄰的三角形的相鄰邊為2個三角形公共的邊[13]，如圖2a和圖2b所示。

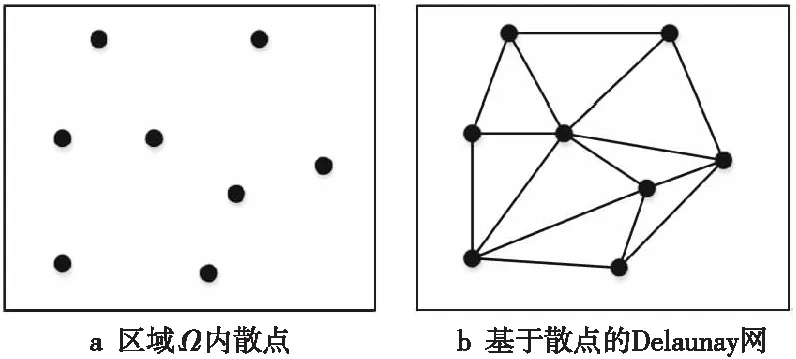
Figure 2 區域Ω內散點和基于散點的Delaunay網圖2 Discrete points in region Ω, and Delaunay triangulation formed by discrete points

定義5(凸包插值算法) 該算法是基于多維空間中生成Delaunay三角網的算法，先后使用凸包生成、環切邊界凸包三角剖分和內插法構建Delaunay三角形，具體步驟可參照文獻[14]。

3 四邊形斯坦納樹連通恢復算法

由于連通恢復問題為NP難問題，本文使用作為啟發式算法的四邊形斯坦納樹算法。若要將區域Ω內的所有分區用中繼節點RN連接，四邊形斯坦納樹連接算法是最節省中繼節點的，算法步驟如下所示：

(1)對區域Ω內的所有分區以4個分區為1組的方式進行組合，枚舉出全部非退化四邊形。

(2)計算枚舉出的全部非退化四邊形的周長，并按照周長從小到大將這些非退化四邊形存入數組NQ[]中。按照數組的順序對所有非退化四邊形進行判別，若非退化四邊形的頂點被其他非退化四邊形占用的個數小于或等于1，則對此非退化四邊形按照定義3的方法標出此非退化四邊形的斯坦納點，將斯坦納點與頂點連接起來即為斯坦納邊，再沿著斯坦納邊部署中繼節點。每條去掉端點的斯坦納邊的中繼節點RN個數用Numse表示，則：

(1)

其中,lengthse表示每條斯坦納邊的長度；R表示中繼節點的通信半徑。連通的非退化四邊形被看作一個分區，繼續抽象為點與其他分區組合為非退化四邊形。

(3)在無法再用非退化四邊形方式連通后，枚舉出剩余分區的三角形組合，按照三角形斯坦納樹連通，無法構建三角形斯坦納樹的分區則與距離最近并且已與主體連通的分區沿直線連通，如圖3所示，SegA～SegL為分區，K1～K6為關鍵節點KN。

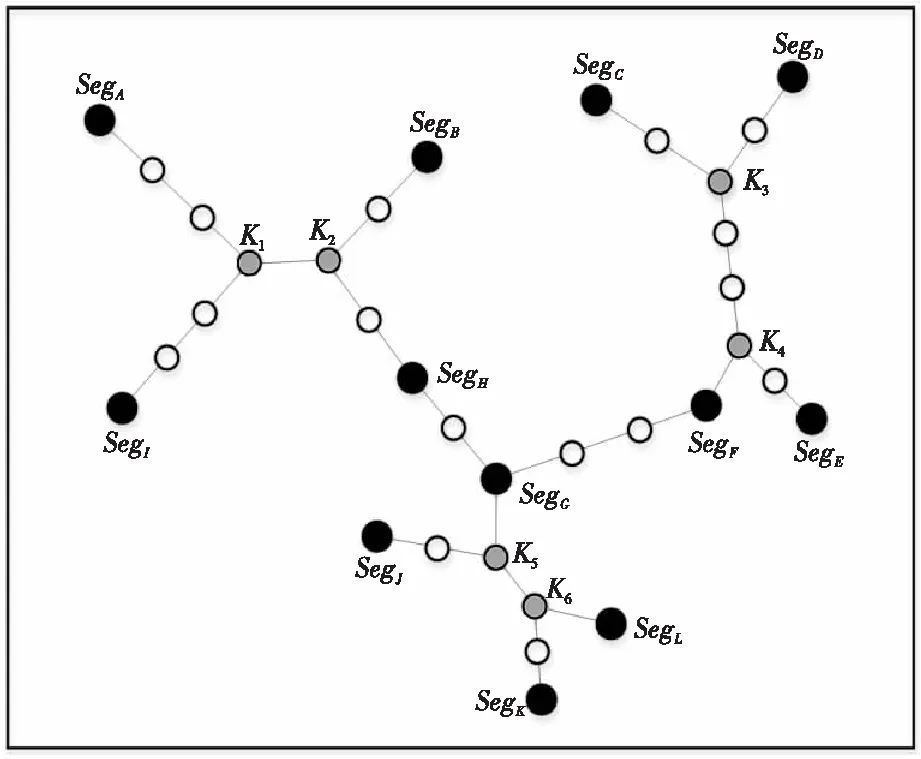
Figure 3 Quadrilateral Steiner connectivity restoration圖3 四邊形斯坦納連通恢復

4 基于泰森多邊形的優化算法

在保證中繼節點數量盡可能少的情況下，本文使用四邊形斯坦納樹的連通恢復算法恢復了癱瘓區域，使所有分區實現了相互連通。為了保證恢復網絡的健壯性，本文針對四邊形斯坦納點所在的關鍵節點KN，使用泰森多邊形的拓撲結構部署備用節點SN，保證在這些關鍵節點損壞時能夠及時移動備用中繼節點替換。

4.1 泰森多邊形部署節點

根據泰森多邊形的性質可知，泰森多邊形每個頂點是與另外2個以上的泰森多邊形的共同頂點，并且泰森多邊形的每個頂點到其對應的2個離散點距離相等，所以對于整個傳感器網絡而言，使用泰森多邊形部署SN可以極大減少SN的部署數量，同時還能保證SN冗余。算法步驟如下所示：

(1)用KN構建Delaunay三角形。

(2)將KN節點編號儲存入數組KN[]中，將三角形編號并儲存入數組TRI[]中，記錄每個三角形所對應的3個KN節點，即TRI[]→KN[]。

(3)根據TRI[]→KN[]，對與每個KN節點相鄰的三角形標號，如圖4所示，對于任意KN，假設此KN為K7，則找出與K7同為一個三角形頂點的另外一個頂點，假設此頂點為K8且此三角形為A，則能夠找出三角形A的第3個頂點并假設此頂點為K9，以K7和K9為頂點，則能找到三角形B的第3個頂點并假設為K10，以K7和K10為頂點，則能找到三角形C的第3個頂點并假設為K11，以此類推，直至回到以K7和K8為頂點時結束此KN相鄰三角形的排序[15,16]。按照排序將相鄰三角形儲存入數組AD[]中。

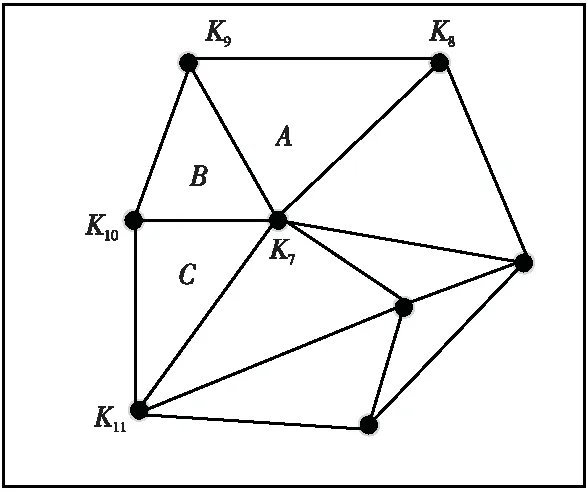
Figure 4 Delaunay triangles are sorted counterclockwise圖4 Delaunay三角形逆時針排序

(4)構建數組TRI[]內每個三角形的外接圓圓心，將相鄰三角形的外接圓圓心連接起來,如圖5所示。

Figure 5 Constructing Tyson Polygon圖5 構造泰森多邊形

(5)將區域Ω中形成的所有泰森多邊形標記并儲存入數組TP[]中，并且記錄每個泰森多邊形所對應的頂點，將頂點儲存入二維數組VER[][]中，并且將關鍵節點KN對應相應的泰森多邊形和泰森多邊形頂點，即KN[]→TP[]→VER[][]。

(6)根據數組VER[][]在所有泰森多邊形的頂點部署SN，將信息儲存入二維數組SN[][]中，則對應關系為KN[]→TP[]→SN[][]，當關鍵節點能量耗盡或者損壞時，移動此KN所對應的SN予以替換。

4.2 基于節點數量權重比較的移動節點選擇

由于多個泰森多邊形共用同一個頂點，故在一個頂點上部署的SN將負責多個KN的替換，所以如何選擇SN去替換KN是保障網絡流暢工作的重要任務。假設失效的KN為Ka，與其相鄰的KN節點分別為Kb、Kc、Kd、Ke，與Ka對應的SN編號分別為Sa和Sb，如圖6所示。算法初始化KN[]→SN[][]信息，分別計算SN節點Sa占KN節點Kb、Kc、Kd對應的SN數量的加權比重，SN節點Sb占KN節點Kd、Ke對應的SN數量的加權比重。選擇SN過程可用數學公式描述為：

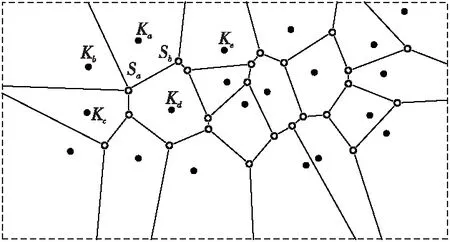
Figure 6 Deploying a standby node圖6 部署備用節點

(2)

其中,SN[i][j]表示KN[i]的備用節點，i=1,2,3,…;j=1,2,3,…；PROPORTIONSN[i][j]表示SN[i][j]占其對應KN的所有備用節點的加權比重；KN[m]SN[i][j]表示與備用節點SN[i][j]對應的所有關鍵節點，m=1,2,3,…;NUMSN表示求KN所對應的SN個數的運算。由式(2)計算出最小加權比重的SN后，移動此備用節點替換失效的關鍵節點。最后在SN節點移動去替換KN節點后，更新KN[]→SN[][]信息。

算法1基于泰森多邊形的優化算法CRAST偽代碼

輸入：分區集合Seg，中繼節點RN通信半徑R。

輸出：需要部署的RN和SN總個數及位置信息。

1. dealQuadrilateral;

2. dealTriangle;

3.IFthere are Segs that are not connectedTHEN

4. Find the shortestedge(u,v),uinSeg1andvinSeg2;

6.ENDIF

7. Define variableNUMBERSTand put the number of relay nodes intoNUMBERST;

8. Constructing Delaunay triangle with KN;

9. Store Delaunay triangle in the arrayTRI[];

10. StoreKNin the arrayKN[];

11.FORarrayKN[]DO

12.KN[] correspond toTRI[];

13. Sort adjacent triangles and store in arrayAD[]

14.FORarrayAD[]DO

15. Construct the center of the circumscribed circle;

16.ENDFOR

17.ENDFOR

18. Connect all centers of the circumscribed circles;

19. Store the vertices of Tyson polygon into arrayVER[][];

20.FORarrayVER[][]DO

21. Deploy SN on vertices and store SN in the arraySN[][];

22.KN[] correspond toSN[][];

23.ENDFOR

24. Define variableNUMBERTPand put the number of standby nodes intoNUMBERTP;

25. Define variableNUMBERRNandNUMBERRN=NUMBERST+NUMBERTP;

26.IFKN[i] is damagedTHEN

26. ReadKN[i]→SN[i][j];

28.FORminjDO

29. Calculate the proportion ofSN[i][m] to the sum of SN numbers of all KN corresponding toSN[i][m];

30.ENDFOR

31. Compare the minimum proportion;

32. MoveSN[i][j] with minimum proportion;

33.ENDIF

34.Output variableNUMBERRN

5 仿真分析

本節采用Matlab進行仿真實驗，在中繼節點部署數量和健壯性2個方面對CRAST算法與1C-SpiderWeb算法和FeSTA算法進行比較。由于1C-SpiderWeb算法和FeSTA算法沒有備用節點替換損壞節點的功能，1C-SpiderWeb算法和FeSTA算法在仿真前期容易因為某個中繼節點損壞而被再次斷連，不能完整地模擬在惡劣環境中的工作表現，故實驗中為1C-SpiderWeb算法和FeSTA算法配備可移動節點，以保證1C-SpiderWeb算法和FeSTA算法能夠在考慮惡劣外部環境影響的仿真中完整運行。實驗將1C-SpiderWeb算法和FeSTA算法的中繼節點以每3個為1組，余下節點成1組進行分組，為每組配備1個可移動節點。本實驗將傳感器網絡區域Ω定義為1500 m×1500 m的正方形區域，通信半徑R∈[40,120]，每20 m取值一次，Segi個數取8，9，10，實驗在多種隨機組合的情況下取平均值，以保證實驗結果的普遍性。

5.1 中繼節點數量

在處理無線傳感器網絡連通恢復的算法中，往往中繼節點數量是非常重要的一項指標，在保證癱瘓網絡恢復連通的同時減少中繼節點數量是無數相關學者的主要研究方向。實驗在3個分區數下，改變中繼節點通信半徑來測試CRAST算法、1C-SpiderWeb算法和FeSTA算法的高效性。

通過如圖7所示的對8個分區、9個分區和10個分區下中繼節點數量與通信半徑的關系對比，可以發現在同一分區下CRAST算法、1C-SpiderWeb算法和FeSTA算法的中繼節點數量隨著通信半徑的增加而減少，由于1C-SpiderWeb算法的特殊拓撲結構，導致1C-SpiderWeb算法與CRAST算法和FeSTA算法相比在分區數越多的情況下，其所需要部署的中繼節點越多。對比圖7可知，在中繼節點通信半徑R較小時，由于CRAST算法中四邊形斯坦納樹結構和泰森多邊形結構都能有效降低中繼節點數量，FeSTA算法所需要的中繼節點數量多于CRAST算法的，當中繼節點通信半徑R較大時，由于CRAST算法的備用節點更多，CRAST算法所需要的中繼節點數量略多于FeSTA算法的。通過對3個算法進行仿真實驗，發現CRAST算法比1C-SpiderWeb算法具有更強的高效性，而在中繼節點通信半徑R較小時,CRAST算法比FeSTA算法更高效，在中繼節點通信半徑R較大時FeSTA算法比CRAST算法高效。

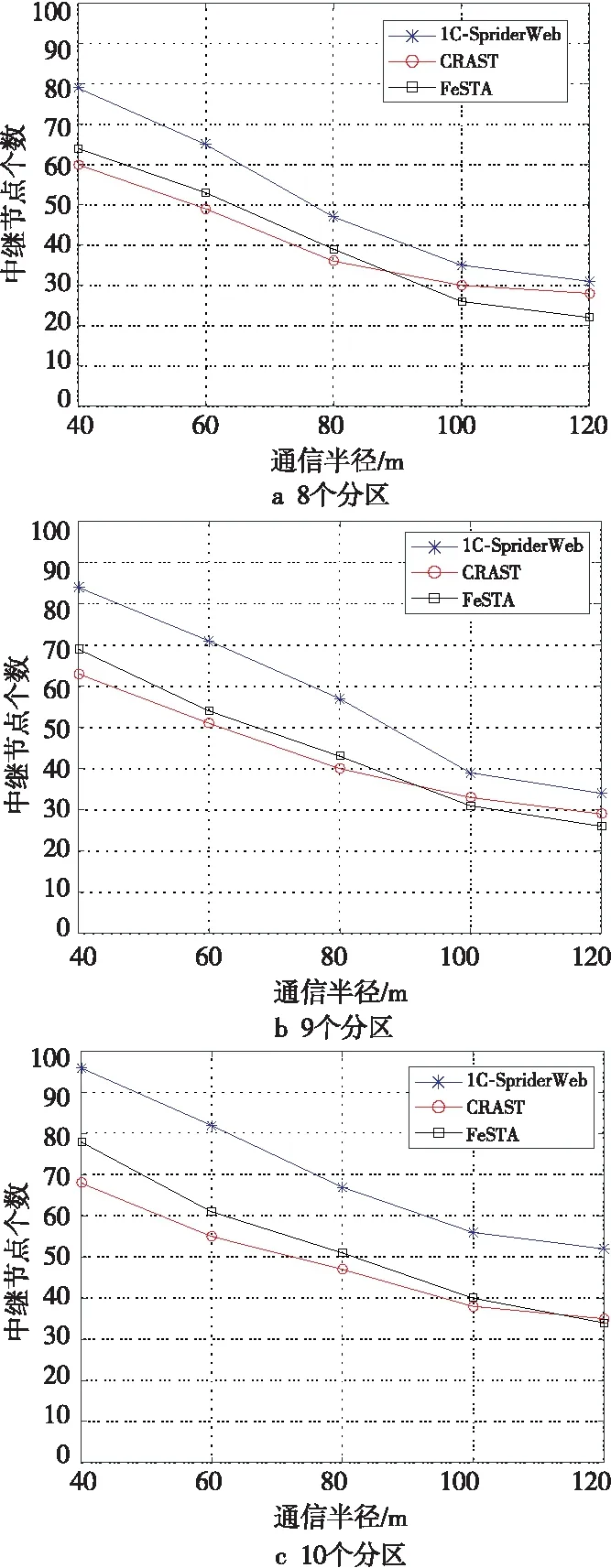
Figure 7 Relationship between the number of relay nodes and the communication radius in different partitions圖7 不同分區數下中繼節點個數與通信半徑的關系

5.2 健壯性

在對癱瘓網絡進行連通恢復后，保證恢復后網絡的健壯性同樣是衡量連通恢復算法優異性的重要指標。傳統無線傳感器網絡連通恢復算法由于其關鍵節點能耗遠大于其他中繼節點，導致關鍵節點工作壽命遠小于其他中繼節點，繼而導致恢復后的工作壽命短。本實驗采用在8個分區、9個分區和10個分區的情況下觀察失效中繼節點與工作壽命之間的關系來驗證CRAST算法、1C-SpiderWeb算法和FeSTA算法在較高故障率下的健壯性，中繼節點通信半徑為80 m。實驗結果如圖8所示。

Figure 8 Working life of three algorithms in different partitions圖8 不同分區下3種算法的工作壽命

通過直方圖對比可知，由于CRAST算法針對關鍵節點優化，CRAST算法的網絡工作壽命比1C-SpiderWeb算法和FeSTA算法的網絡工作壽命更長，而1C-SpiderWeb算法和FeSTA算法由于關鍵中繼節點消耗過多能量，導致網絡的工作壽命無法達到最大化。

6 結束語

本文提出的CRAST算法旨在解決無線傳感器網絡由于部分中繼節點失效導致網絡被分割成多個分區的問題，通過構建四邊形斯坦納樹和泰森多邊形實現高效且健壯的連通恢復。通過多個實驗與1C-SpiderWeb算法和FeSTA算法進行對比，驗證了CRAST算法相比1C-SpiderWeb算法和FeSTA算法具有更出色的高效性和健壯性。由于本文算法是基于二維空間的算法，無法解決自然環境中非平面地形的部署，所以接下來的工作將針對三維空間的網絡連通恢復進行研究，以保證在三維空間中網絡出現癱瘓后能夠及時恢復。