巧用數形結合解決電學疑難問題
雷登玉 簡涵林
【摘 要】在研究物理問題時,可以通過數形結合的方法將抽象的數量關系與直觀的幾何圖形、位置關系結合起來,即通過抽象思維與形象思維結合,可以使復雜問題簡單化,抽象問題具體化。本文結合筆者的教學實際與經驗,通過典型例題來體會數形結合在初中物理電學中的妙用,同時通過圖像讓物理情景生動的呈現,易于學生理解和提升。
【關鍵詞】U-I圖像;電功率變化;電學比例;四維一體
一、利用U-I圖分析電功率的變化
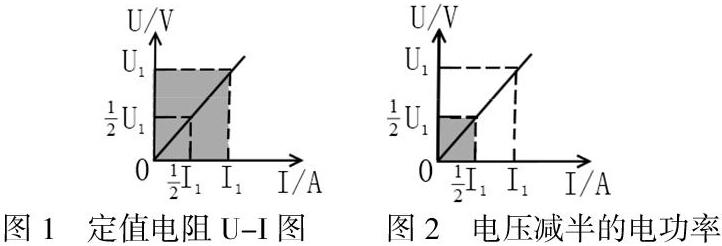
1.定值電阻U-I圖像
如圖1為定值電阻R的U-I圖,在圖像中某點的U與I的比值表示該電阻的大小,U與I的乘積表示電阻在該電壓下的電功率,同時電功率還可以理解為此處U與I圍成的面積,如圖1中陰影部分的面積。通過面積能夠反映電功率的大小的這個知識點,可以幫助學生更好的找到電功率的變化。
初中物理經常出現的考題就是一個定值電阻兩端電壓變為之前的一半,則電功率變為之前的多少。這種題目學生易錯在認為電流不變,則電功率為之前的二分之一。但是如果能夠結合圖像來進行分析,此時的電功率就是圖2中的陰影部分的面積,剛好是之前的四分之一,學生就比較好理解了。
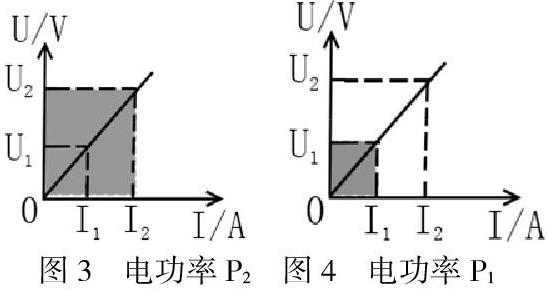
在教學中,學生一直存在一個疑點,就是為什么電功率的變化不等于電阻兩端電壓的變化乘電流的變化量,之前的教學我們也是一直采用數學證明的方式給學生進行講解,但是基礎較弱的學生根本就不能理解,后面發現用圖像給學生分析,他們突然就豁然開朗。
如圖3,此時陰影部分面積即表示電阻兩端電壓為U2,電流為I2時的電功率P2,圖4中此時陰影部分面積表示電阻兩端電壓為U1,電流為I1時的電功率P1。而電阻兩端的電壓從U1變到U2,電流從I1變到I2的電功率變化是不等于(U2-U1)(I2-I1)的,我們可以從圖像來進行理解。
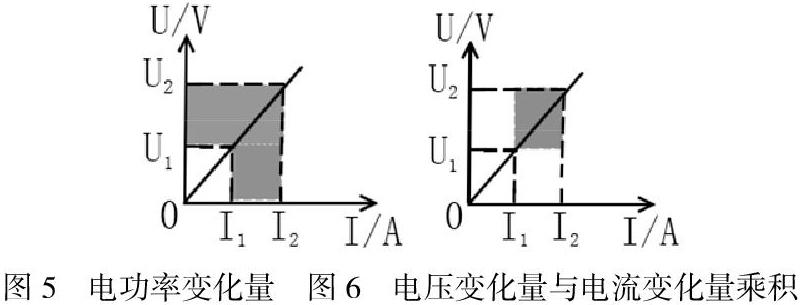
這個過程中電功率的變化為U2I2-U1I1,即圖3的陰影面積減去圖4的陰影面積,減了之后剩余的面積如圖5所示。而(U2-U1)(I2-I1)表示的面積卻是圖6中的陰影部分,明顯小于電功率的變化,這樣通過圖像就巧妙的讓學生突破了這個疑點。
2.小燈泡U-I圖像
我們常看到這么一個物理題目,將“220V 100W”的燈泡兩端電壓降為原來的一半或者將其中的電流降為原來的一半,兩種情況下燈泡的實際電功率一樣嗎?這樣的題目在之前的教學中我們更注重的是去給學生分析,證明,但是效果并不是很理想。后來采用圖像的方式,學生就容易理解了。
如圖7陰影部分表示電壓減小為之前一半時的電功率,通過圖像我們還可以發現此時的電流時大于額定電流的一半,所以這時候的電功率大于四分之一的額定電功率。如圖8陰影部分則表示電流減小為之前一半時的電功率,此時的電壓是小于額定電壓的一半,所以這時候的電功率小于四分之一的額定電功率。當然,我們可以直接看陰影面積的大小便可判斷出電壓減小為額定電壓一半時的電功率更大。
二、“四維一體”攻破電學難題
1.構建并聯電路巧解比例問題
標有“220V 100W”L1和“220V 50W”L2的兩只燈泡,燈泡電阻不隨溫度變化而變化,將其串聯在220V電路中,電功率之比為多少?若將其并聯在220V電路中,通過它們的電流之比為多少?
這樣的題目,我們可以利用四維一體的方法來進行巧解,因為題目問的大多問題是比例問題,而電路中所有的比例問題都與電阻的比值有關,所以只要知道了電阻的比值,所有問題都迎刃而解。因為這兩個燈泡的額定電壓是一樣的,我們可以將它們構建在一個電源電壓為220V的電路中,如圖9所示,此時P1:P2=2:1,由并聯中電功率之比等于電阻的反比,則可以知道R1:R2=1:2,所以串聯在220V電路中時,它們電壓之比U1:U2=R1:R2=1:2,并聯在220V電路中,通過它們的電流之比為電阻的反比,即I1:I2=2:1。通過構建一個圖形,可以讓學生快速的進行判斷,從而減小計算的錯誤率。
2.構建并聯電路巧解動態問題
其實四維一體最大的妙用是解決電學的動態問題。比如我們經常會看到這么一個類似題目。定值電阻R0和滑動變阻器R串聯在電路中,如圖10所示,電源電壓恒定不變,當滑動變阻器接入阻值為R時,R0兩端電壓為15V,當滑動變阻器接入阻值為2R時,R0兩端電壓為12V,當滑動變阻器接入阻值為2R+20Ω時,R0兩端電壓為9V,則電源電壓和定值電阻R0的阻值。
這個題目用最常規的方法解答就是根據電源電壓不變,列三個方程,求解三元一次方程組,但是對于數學計算能力薄弱的學生來說,很難做正確。而且很多學生一看是三個方程,直接放棄了。但是我們如果利用四維一體來進行解題,很快就可以算出正確答案。
如圖11所示,我們把三個不同時刻的電路并聯在同一個電路圖中,因為R0是定值電阻,則I1:I2=15V:12V=5:4,并聯電路中,電流之比等于電阻的反比,則(R0+R):(R0+2R)=4:5,既可以算出R0=3R,得出了電阻之間的關系后,就可以通過兩電阻串聯電壓之比等于電阻之比,求出電源電壓為20V。然后根據最后一次電阻R0分的電壓為9V,則(2R+20Ω)分的電壓為11V,根串聯中電壓比等于電阻之比解出R為12Ω,則R0=3R=36Ω。
三、結束語
數形結合在教學中的確能夠幫助我們解決很多問題,但它也有一定的局限性,所以在我們的教學中,我們盡可能的多給學生提供一些解題的方法和技巧,讓每個學生找到適合他自己的解題方法。
參考文獻:
[1]李俊鵬. 控制變量、轉化以及數形結合的思想在電學實驗數據處理中的應用[J]. 物理教學探討,2019,037(001):49-52,54.

