圍巖蠕變對運營隧道襯砌安全性的影響

錢文喜，耿大新，梁國卿

(1. 江西省公路工程有限責任公司，江西 南昌 330006；2. 華東交通大學 土木建筑學院，江西 南昌 330013；3. 江西省天馳高速科技發展有限公司，江西 南昌 330103)

0 引言

公路隧道圍巖極其復雜的非線性、各向異性和隨時間變化的力學屬性，決定了圍巖與襯砌結構相互作用的復雜性。在軟弱圍巖隧道運營期間，二次襯砌與圍巖可以同時作為承載主體，而圍巖蠕變對隧道穩定性及襯砌結構安全性具有重要的影響。因此，許多學者開展了相關研究：劉甲榮等[1]考慮圍巖蠕變效應，分析了不同埋深及偏壓條件下襯砌結構表面拉、壓應變與損傷值之間的關系；李建軍等[2]基于Burgers模型分析了圍巖蠕變作用對襯砌結構內力的影響；王迎超等[3]基于廣義Kelvin模型分析了不同時機支護下襯砌結構的受力規律；徐國文等[4]建立錨桿-圍巖復合體流變模型分析了圍巖蠕變作用對裂損襯砌長期安全性的影響；Guan等[5-6]通過對Ureshino隧道進行跟蹤監測，分析了圍巖蠕變與隧道持續變形的關系；王中文等[7]考慮隧道圍巖的蠕變特性，利用初襯變形理論公式分析了隧道初襯最終變形及二次襯砌合理的支護時機；唐葭等[8]基于Burgers模型推導出了考慮圍巖蠕變效應的圍巖抗力系數公式，進而分析了紅砂巖隧道圍巖的抗力系數；Fan等[9]采用室內模型試驗對泥質軟巖隧道圍巖的蠕變力學行為進行了研究。此外，左昌群等[10]考慮軟弱圍巖蠕變特性，分析了不同支護形式下圍巖與初期支護結構的相互作用；文獻[11-14]對軟巖隧道圍巖的蠕變特性、蠕變模型及蠕變參數進行了大量研究。

目前，常用的模擬隧道圍巖蠕變的元件組合模型有Kelvin模型、西原模型、Burgers模型、Bingham模型等[15]。但不同地區、不同類別的巖石力學性狀差異較大，需要選擇適用的元件組合模型來描述巖石的蠕變特性。本研究以江西九景高速公路隧道為依托，基于該隧道Ⅳ級圍巖區段泥質粉砂巖蠕變試驗結果，利用Cvisc黏彈塑性模型對其蠕變模型及參數進行辨識，進而分析圍巖蠕變效應對運營隧道襯砌結構安全性的影響，以期為公路隧道運營期的管理和養護提供參考。

1 工程概況

九景高速公路隧道為雙向兩車道，隧道凈寬10.25 m，凈高7.425 m，洞身襯砌采用三心圓曲墻式，運營時間已超過10 a。洞身穿越地層巖性主要為泥盆系細砂巖和志留系粉砂巖，巖體完整性以較完整～較破碎為主。其中，Ⅳ級圍巖隧道斷面如圖1所示。

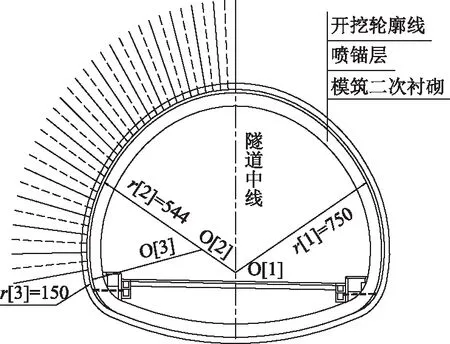
圖1 Ⅳ級圍巖復合式襯砌Fig.1 Composite lining of Grade IV surrounding rock

2 砂巖蠕變模型辨識

2.1 蠕變試驗

通過單軸抗壓強度試驗，獲得了5組φ50×100 mm 圓柱體巖樣破壞時最大軸向壓力Pi和抗壓強度Rci(見表1)，其中，i=1,2,…,5。巖樣取自九景高速公路隧道，為泥質粉砂巖，無明顯層理，且節理裂隙不發育。

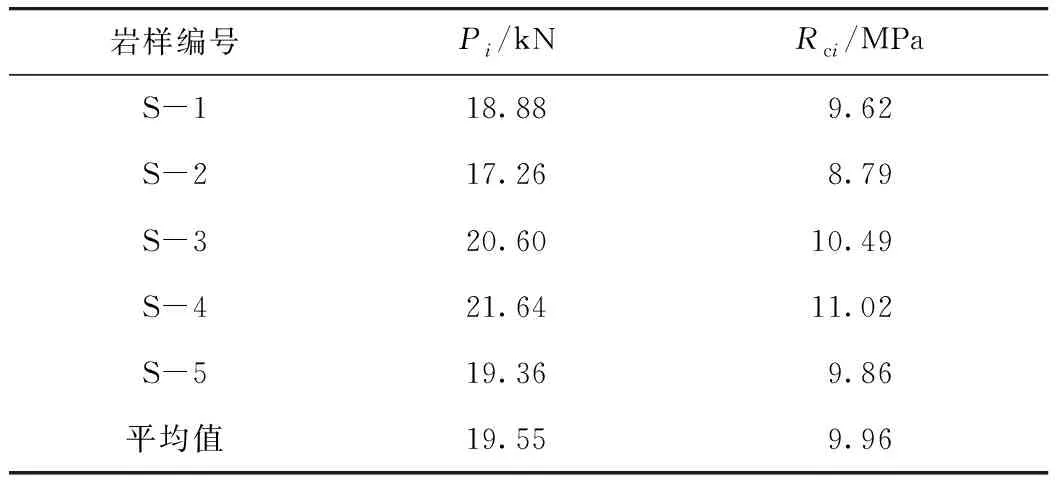
表1 泥質粉砂巖單軸抗壓強度Tab.1 Uniaxial compressive strength of argillaceous siltstone

通過YSR-300型巖石三軸蠕變試驗系統對泥質粉砂巖進行單軸壓縮蠕變試驗，獲得了巖樣在0.7Rc，0.8Rc，0.9Rc應力水平下較能反映其蠕變特性的試驗數據曲線(見圖2)。

圖2 不同應力水平下的非線性擬合結果Fig.2 Nonlinear fitting results at different stress levels

2.2 蠕變模型與參數確定

Cvisc模型由Kelvin體、Maxwell體和塑性體共同構成(見圖3)。當應力水平較低時，變形速率逐漸減小進入衰減蠕變階段，之后逐漸趨于某一恒定值進入穩定蠕變階段；當應力水平等于或超過某一臨界應力值σs后，逐漸轉化為加速蠕變過程。

在一維應力狀態下，Cvisc模型蠕變本構方程為：

(1)當σ<σs時，

(1)

(2)當σ≥σs時，

(2)

式中，EK、EM分別為Kelvin體、Maxwell體的彈性模量；ηK、ηM分別為Kelvin體、Maxwell體的黏性系數；σ0為常應力；εP為塑性體應變。

圖3 Cvisc模型Fig.3 Cvisc model

蠕變方程(1)，(2)屬于非線性函數形式，為求其中的蠕變參數，可采用最小二乘法中Boltzmann法處理試驗數據，即采用線性疊加的間接方法求解[16]。結果表明，圖2中的擬合曲線與試驗數據曲線的相關系數R2在0.92～0.96之間，因此，可以認為Cvisc模型能夠描述泥質粉砂巖的衰減蠕變和穩定蠕變關系。根據室內蠕變試驗結果，得到Cvisc模型在0.7Rc，0.8Rc，0.9Rc應力水平下的蠕變參數(見表2)。

3 數值模擬與結果分析

3.1 模型建立

以Ⅳ級圍巖公路隧道襯砌結構為研究對象，利用FLAC3D建立兩車道公路隧道三維數值模型，如圖4所示。隧道模型左、右側均距離隧道中心線50 m(約4倍隧道開挖跨度)，洞周拱頂以上取24 m，仰拱以下取36 m，縱向取60 m。圍巖采用實體單元模擬，本構模型采用Mohr-Coulomb模型，初始地應力場僅考慮重力作用。此時，邊界條件采用位移約束，即左右兩側采用水平位移約束，頂部自由無約束，底部采用豎向位移約束。

表2 Cvisc模型參數Tab.2 Parameters of Cvisc model

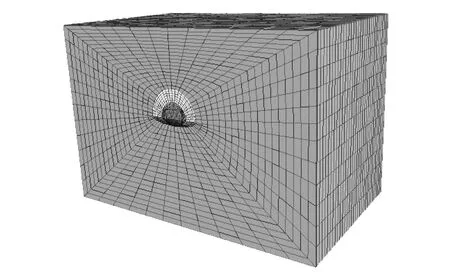
圖4 三維隧道數值模型Fig.4 3D tunnel numerical model

在隧道施工期間，假定圍巖在開挖條件下的變形完全為彈性或同時含有塑性變形。因此，Cvisc模型中用以描述圍巖時效變形的黏性元件應不發生作用，圍巖變形僅由模型中的彈性或塑性元件來體現，故此時蠕變方程(1)、(2)中的t=0。于是，通過命令(SET CREEP OFF)來屏蔽蠕變模型的時效作用，即僅對圍巖進行靜力計算分析。其中，Ⅳ級圍巖的物理力學參數見表3。

表3 圍巖物理力學參數Tab.3 Physical and mechanical parameters of surrounding rock

通過提高洞周圍巖變形模量、黏聚力等指標的方法來模擬錨桿加固區的力學行為，加固區厚度取4 m，Ⅳ級圍巖錨桿加固區域的物理力學參數見表4。

假定圍巖與初期支護分擔60%釋放荷載，二次襯砌分擔40%釋放荷載。于是，在施加襯砌前，對隧道周邊圍巖進行某一比例卸荷，即選定應力釋放

表4 錨桿加固區圍巖物理力學參數Tab.4 Physical and mechanical parameters of surrounding rock in anchor reinforcement area

率λ=0.6。采用實體單元模擬噴混凝土層，本構模型采用線彈性模型；二次襯砌采用襯砌結構單元(Liner)模擬，初期支護的物理力學參數見表5。

表5 初期支護物理力學參數Tab.5 Physical and mechanical parameters of initial support

考慮到噴混凝土層與二次襯砌之間防水層的影響，單元界面接觸參數選取見表6。

表6 單元界面接觸參數Tab.6 Contact parameters of unit interface

在隧道運營期間，假定圍巖總變形由開挖導致的彈塑性變形和蠕變變形共同構成。因此，Cvisc模型中用以描述圍巖時效變形的黏性元件開始發生作用。于是，基于靜力計算分析結果，通過命令(SET CREEP ON)來開啟蠕變模型的時效作用，即對圍巖進行蠕變計算分析。其中，Cvisc模型所需的Mohr-Coulomb強度參數見表7。對泥質粉砂巖在0.7Rc,0.8Rc，0.9Rc應力水平下的蠕變參數進行平均值計算，得到圍巖蠕變參數。

表7 圍巖蠕變參數Tab.7 Creep parameters of surrounding rock

Cvisc模型的最大蠕變時間步長為：

(3)

為了使計算模型更好地收斂，設置蠕變計算時間步長為2.5×10-3，最大蠕變時間步長為5.0×10-3，最小蠕變時間步長為5.0×10-4。將蠕變計算總歷時定為3 650 d(即蠕變計算的總歷時為10 a)[17]。

3.2 結果分析

我國《公路隧道設計規范》[18](JTG3370.1—2018)規定，公路隧道支護結構需滿足驗算的安全系數要求。規范規定混凝土偏心受壓構件的抗壓和抗拉強度驗算需滿足式(4)和式(5)。

KcN≤φαRαbh,

(4)

(5)

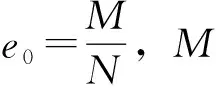
在隧道運營10 a過程中，單考慮圍巖蠕變作用，將數值模擬的計算結果代入式(4)和式(5)得到二次襯砌拱頂、拱肩和拱腰位置安全系數隨時間的變化曲線(見圖5)。從圖中可以看出，隨著二次襯砌服役時間的增加，拱頂、拱肩和拱腰位置安全系數總體呈逐漸減小的趨勢，其中拱頂處安全系數降低最為顯著，表明圍巖蠕變變形壓力隨著時間逐漸增加。

圖5 襯砌結構安全系數隨時間變化曲線Fig.5 Curves of lining structural safety factor varying with time

隧道運營10 a后，二次襯砌軸力、彎矩、安全系數的分布，見圖6～圖8。從圖中可以看出，襯砌結構最大軸力出現在邊墻位置，為2 700 kN，并沿拱頂和拱底位置環向減小，最小軸力出現在拱底位置，為757 kN；最大正彎矩出現在拱腳位置附近，為312 kN·m，最大負彎矩出現在拱底位置，為40.9 kN·m；安全系數最小值出現在邊墻位置，為2.9，最大安全系數出現在仰拱底位置，為72.3。這表明，在同一支護時間，二次襯砌支護結構承載較小的位置(即安全系數較高的位置)，圍巖的蠕變變形量較大，因而支護結構承受的圍巖壓力相對較小，但過小的支護承載又會導致圍巖蠕變變形而增加圍巖壓力，進而不利于襯砌結構的長期安全。

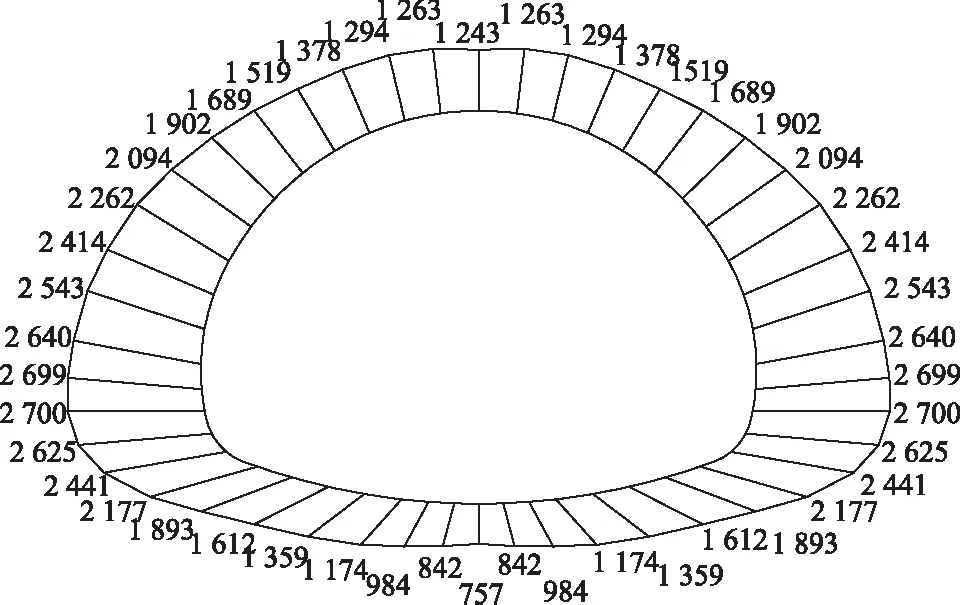
圖6 襯砌結構軸力(單位: kN)Fig.6 Axial force of lining structure(unit：kN)

圖7 襯砌結構彎矩(單位: kN·m)Fig.7 Moment of lining structure(unit：kN·m)

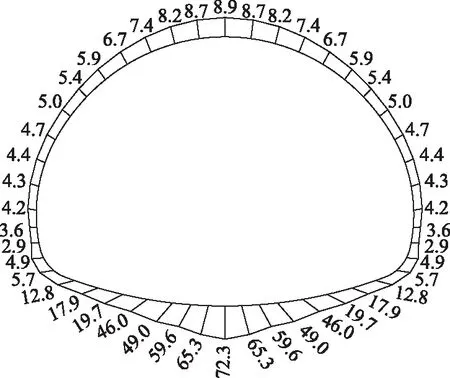
圖8 襯砌結構安全系數Fig.8 Safety factor of lining structure

3.3 隧道埋深的影響分析

在隧道運營10 a過程中，考慮圍巖蠕變作用，在11.7 m(hq)，23.4 m(2hq)，35.1 m(3hq)，46.8 m(4hq)的隧道埋深下，將數值模擬的計算結果代入式(4)和式(5)得到二次襯砌拱頂、拱肩、拱腰位置的安全系數隨其服役時間的變化曲線(見圖9)。從圖中可以看出，在圍巖蠕變變形壓力作用下，隨著隧道埋深的增加，襯砌結構拱頂、拱肩、拱腰位置在同一服役年限的安全系數逐漸增大，其中拱頂位置的增長幅度最大。這表明，在同一支護時間，二次襯砌支護結構的承載隨著隧道埋深的增加而減小，即圍巖自身承擔了較大部分的因蠕變變形而增加的圍巖壓力，從而對二次襯砌的長期安全有利。

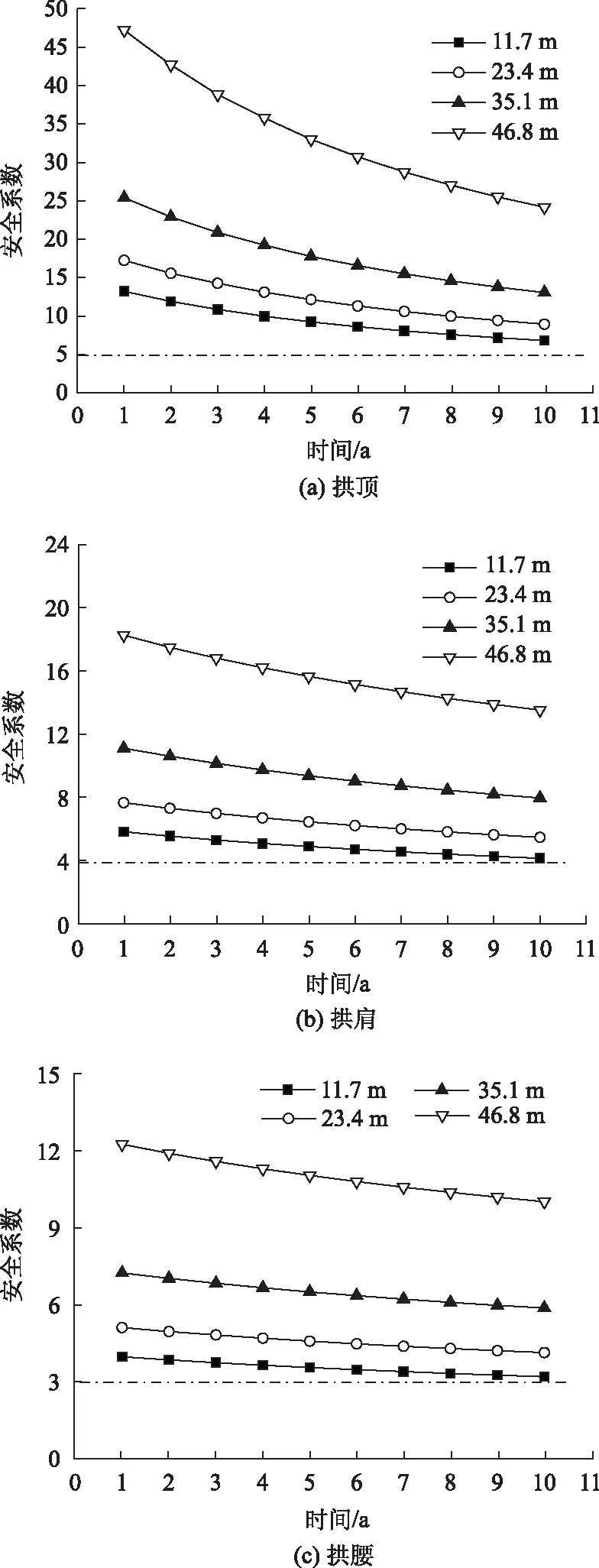
圖9 不同埋深下襯砌安全系數隨時間變化曲線Fig.9 Curves of lining safety factor varying with time under different depths

4 結論

以九景高速公路隧道為背景，利用有限差分軟件FLAC3D建立了兩車道公路隧道三維數值模型，考慮了圍巖蠕變作用，對Ⅳ級圍巖公路隧道在10 a運營期間襯砌結構的安全性進行了分析，得出以下結論：

(1)通過對泥質粉砂巖進行單軸壓縮蠕變試驗，并對試驗數據曲線進行非線性擬合。結果表明，其相關系數R2在0.92～0.96之間，可認為Cvisc模型能夠很好地描述泥質粉砂巖的衰減蠕變和穩定蠕變關系。

(2)單考慮圍巖蠕變作用，在同一支護時間，二次襯砌安全系數較高的位置，支護結構承受的圍巖壓力相對較小，圍巖的蠕變變形量較大，但過小的支護承載又會導致圍巖蠕變變形而增加圍巖壓力，進而不利于運營隧道襯砌結構的長期安全。

(3)同時考慮隧道埋深的影響，在同一支護時間，二次襯砌支護結構的承載隨著隧道埋深的增加而減小，即圍巖能夠承擔較大部分的因蠕變變形而增加的圍巖壓力，從而對運營隧道襯砌結構的長期安全有利。