載荷分布對空氣靜壓軸承振動特性的實驗

王繼堯，龍威,*，吳蜜蜜，趙娜，畢玉華

1. 昆明理工大學 機電工程學院，昆明 650500

2. 昆明理工大學 云南省內燃機重點實驗室，昆明 650500

基于氣體潤滑技術的空氣靜壓軸承具有高速、精密、低摩擦的特點，因而被廣泛應用在慣導陀螺馬達、空間模擬裝置、低速伺服轉臺等航空航天領域[1-2]。特別是在大型高精度空氣靜壓軸承轉臺中，作為核心部件的空氣靜壓軸承不僅要保障轉臺實現極高的回轉精度，同時要求振動小、噪聲低，并且具有高穩定性和耐振動沖擊能力。支撐部件的間隙、支撐剛度和不平衡分布等動力學參數和氣動流場氣動力等隨著工作條件和支撐系統狀態變化而變化，使得系統結構振動具有非線性時變特征，因此，對空氣軸承動力學特性要求更為嚴格。根據沖擊射流理論和氣動彈性力學可知，氣膜入口在一定流速的來流作用下，氣浮塊會受到流向以及橫向的周期性變化的脈動壓力，作為一個彈性支撐，脈動壓力會引起結氣浮塊在平衡位置發生周期性振動，這種振動又會反過來改變氣膜內流場結構[3]。氣膜流體與固體氣浮軸承之間相互耦合的渦激振動沿著流場運動方向傳播，不僅影響系統的定位精度和進給精度，也會降低整個系統的加工精度和檢測精度[4-5]。特別是當軸承表面負載分布不均勻時，載荷的重力不再通過支撐氣膜的形心。軸承表面產生橫傾角，氣膜厚度不再均勻，導致氣膜壓力分布發生變化，并在側向推力平面上產生壓力分量。同時，軸承支撐面傾斜引發氣膜流場變化，不僅會引起較大的軸承間隙測量誤差，當局部渦激振動強度增強或與外界干擾信號發生諧振時，則會引起氣膜失穩，甚至引發氣錘現象[6-7]。因此，提高空氣靜壓軸承的傾斜剛度和阻尼系數及研究載荷分布對氣膜流場的影響對提高空氣軸承穩定性和使用精度具有重要意義。

國內外學者在這方面做了大量有益探索，其中一部分學者通過研究空氣靜壓軸承的靜/動態傾側特性進行了理論分析。Majumdar和Singh[8]對傳統的多個凹槽止推軸承進行了深入比較，給出了方形凹槽止推軸承性能的設計曲線。在此基礎上Singh和Rao[9-10]研究了偏置載荷作用下空氣靜壓多孔矩形止推軸承的靜態傾斜特性，對不同工作參數的靜態特性進行了數值計算，并給出了氣浮傾斜特性隨氣浮塊形狀、不同工作條件的變化規律。Al-bender和Brussel[11]采用小擾動法對圓形空氣靜壓軸承的動態傾斜特性進行了研究，得到了傾斜剛度和阻尼系數隨工作氣膜改變的影響規律。Nakamura和Yoshimoto[12-13]研究了帶有復合節流器的空氣靜壓止推軸承傾斜力矩作用下的線性導軌系統中的靜態傾斜特性，并與傳統的小孔節流器止推軸承的特性進行比較，闡明了復合節流器空氣靜壓止推軸承的實用性。然而，在實際氣浮工作中，由于熱變形、結構變形或工作偏載誤差等原因，軸承不對中運動導致氣膜厚度和壓力分布不均勻，導致空氣靜壓軸承靜壓剛度顯著降低，對氣浮系統的運動精度有很大的影響，甚至氣浮支撐不穩定[14-16]。此外，空氣靜壓推力軸承的剛度和阻尼等動態特性發生變化，也會引起氣浮系統的微振動。Long和Deng[17]采用有限體積法計算了不同傾角下軸承的側向力，研究了不同氣腔直徑和深度在發生傾斜角時對軸承的橫向力產生的影響。Yoshimoto等[18]從理論和實驗上研究了軸傾斜運動下帶有復合節流器的空氣靜壓矩形雙墊推力軸承的動態特性。Jiang等[19-20]利用線性擾動建立了軸承的雷諾方程，研究了軸承參數對軸承靜、動態特性的影響，并分析了多孔介質對空氣軸承動剛度和阻尼系數的影響。Xu和Jiang[21]建立了3自由度氣動靜力推力軸承模型，并得到了軸承的穩定性、不平衡響應和強迫響應，全面研究了傾角和轉速對軸承動態剛度和阻尼系數的影響。雖然國內外學者就空氣靜壓軸承的偏載和動特性開展了相關的研究，但是主要集中在數值模擬和動特性系數(動剛度和動阻尼)的分析上，而對載荷分布與穩定性之間的關系與成因缺乏充分的解釋和分析。

因此，本文以圓盤形中心供氣小孔節流空氣靜壓軸承為對象，基于渦激振動原理和振蕩流體力學理論，在求解非定常流體力學方程的基礎上，對空氣靜壓止推軸承表面載荷分布不均勻時氣浮傾斜特性隨工作條件的變化規律開展研究。從理論和實驗兩方面研究空氣靜壓止推軸承的微振動，并分析了傾斜力矩對軸承氣膜內部渦動能量的影響，給出了不同工況下軸承偏載及正載下的工作條件和參數要求，明確偏載特性對空氣靜壓止推軸承穩定性的影響因素及其相關結論。

1 理論模型

空氣靜壓軸承通過節流器形成的壓力在氣膜內形成壓力梯度，氣體流場的變化引起氣膜內發生氣旋渦動從而引發渦流激振效應。對于軸承的動特性和穩定性分析，歸根到底取決于軸承氣膜內流動激振的分析。現有研究氣膜內流體動力學問題的方法是建立在雷諾方程基礎上的，但是由于氣膜厚度在微米級，傳統方法認為速度參數沿氣膜厚度方向變化，而壓力沿氣膜厚度方向不變，從而對Navier-Stokes方程進行定常簡化，這樣得到的雷諾方程本質是一個定常的方程。為了將雷諾方程應用于求解軸承的動態特性，就必須將流動參數與時間變量關聯起來。采用振蕩流體力學原理分析氣膜激振，首先求解氣膜內不做振動或渦動時的流場(即：定常場)，然后以定常參數作為已知值再求解氣膜的振蕩流場(即：振蕩速度場和振蕩壓力場)，通過對氣膜表面振蕩壓力的積分，即可得到作用在軸承表面的非定常流動力。由于微幅簡諧振蕩流的特點，可以將非定常參數表示為定常參數與振幅參數的關系，因此，用于描述空氣靜壓軸承工作氣膜流場特性的非定常連續方程、動量方程、能量方程等就可以轉化為相應的振幅連續方程，振幅動量方程和振幅能量方程等，從而構成振蕩流體力學的基本方程。

當空氣軸承負載重心稍微偏離氣膜形心導致氣浮軸承發生傾斜時，氣膜流場特性參數分布跟隨改變，直接影響氣膜支撐系統靜態和動態特性。

圖1所示為圓盤型中心供氣小孔節流空氣靜壓止推軸承在表面載荷分布發生偏載前后的結構示意圖及相關參數：軸承外徑D=200 mm；供氣孔直徑d0=0.2 mm；氣腔直徑d1=3 mm；氣腔深度δ=0.2 mm；環境壓力pa=0.1 MPa；供氣壓力ps=0.2～0.5 MPa；氣膜間隙h=10～40 μm；環境溫度T=293 K；氣體動力黏度η=1.833 ×10-5Pa·s；氣體密度ρ=1.205 kg/m3；氣體常數R=288 J/(kg·K)。

如圖1(a)所示，氣膜流場的入口是位于圓盤型氣浮軸承中心的小孔節流器，氣源氣體從供氣孔徑向均勻的呈直線向外流出，形成均勻的壓力氣膜。由于流動是徑向的，根據流動連續性原理，通過坐標系內任意分度圓圓柱的流量Q都相等：

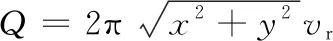
(1)

式中：vr為半徑方向流速。即

(2)

其中：u和v分別為沿x和y方向的氣流速度。

根據流函數的定義并令積分常數為零，可得此時供氣孔處流函數：

(3)

根據射流理論可知，高壓氣體從供氣孔流出就會與周圍介質發生劇烈的動量交換和紊動擴張，在流體的外邊界形成速度不連續的間斷面，并將周圍原有靜止的氣體分子卷吸到射流過程中，從而形成渦旋，從圖1中可以看到氣旋集中發生在過渡區并沿著壁面射流區流出，在氣腔底部中心定義坐標系Oxy，氣體沿供氣孔z方向流動，當氣體通過過渡區后，射流方向發生改變，流動速度沿x和y方向運動。定義氣腔高度為δ，氣膜厚度為h，正載下氣膜厚度為h0,則供氣出口總的沖擊高度為h=δ+h0。

當正載工作時如圖1(a)所示，軸承氣膜內x、y方向的速度[22]為

(4)

(5)

式中：p為壓力；μ為氣體黏度(Pa·s)；u1，u2，v1，v2為軸承兩側面在x，y方向上的運動速度(m/s)，當z=0時，u=u1，v=v1，當z=h+δ，u=u2，v=v2。

根據動量守恒可知，過渡區中壓力分布規律[23]可以表示為

(6)

式中：pm為軸線壓力，則p應滿足：

(7)

壁面射流區中p滿足：

(8)

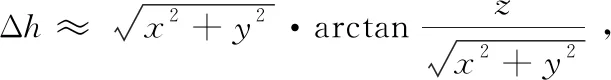
(9)

則壁面射流區中p滿足：

(10)

2 實驗原理及實驗過程

2.1 實驗原理和裝置

實驗原理圖如圖2所示，實驗中主要測試空氣靜壓軸承的承載力和氣膜剛度的大小以及空氣靜壓軸承自激微振動特性及幅頻特性。對不同工作條件下的微振動大小進行測量并對比研究。微振動測試裝置主要由氣源、過濾器、加載裝置、檢測裝置和數據處理部分等組成。

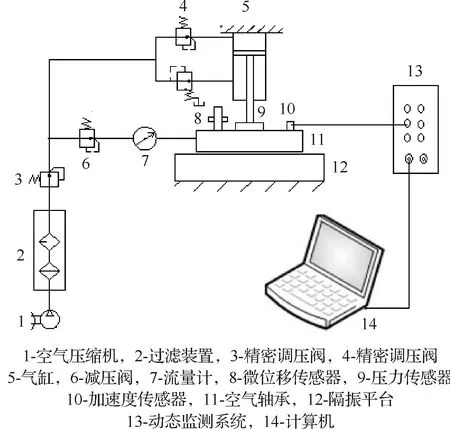
圖2 氣浮微振動測試原理圖

實驗時被測空氣靜壓軸承水平置于00級大理石隔振平臺上，氣源壓力氣體經過過濾裝置除去氣體中水分、灰塵等雜質，并經SMC高精密調壓閥輸送到氣路中。采用氣缸加載的方式控制負載的大小，通過控制氣缸的進氣量和壓力調節對氣浮軸承施加的負載壓力，氣浮軸承承載由壓力傳感器測得。隨著供氣壓力的變化，相同負載條件下氣膜厚度會隨之改變，氣膜厚度由微位移傳感器測得；為保證氣膜厚度可控可測，實時根據供氣壓力大小調整負載大小，以保證氣膜厚度精確可控。微振動信號由貼敷在軸承表面的3個單軸加速度傳感器(PCB Piezotronics)檢測。為檢測三維氣旋對氣浮軸承表面的作用效果，分別在氣膜高度方向和垂直氣膜方向上布置兩組加速度傳感器。數據處理部分采用比利時公司的LMS動態檢測系統。

2.2 實驗條件及設備

實驗條件為標況大氣壓、室溫25 ℃、濕度40%～50%， 隔振平臺為00級花崗石平臺，三軸方向的固有頻率均為1.2～2.0 Hz。

圖3為氣浮微振動測試實驗臺和相關設備。測試實驗臺由振動測試和數據采集裝置組成，如圖3 (a) 所示實驗臺采用光學隔振平臺，氣源裝置采用空氣壓縮機，經過高精密過濾減壓組件后，將高壓氣體同時通入加載氣缸和氣浮軸承中，耗氣量由流量計得到。圖3(b)為實驗測試部分。測得微振動信號由頻譜儀實時采集和記錄，處理后最終顯示在PC屏幕上。如圖3(c)所示：壓力傳感器(BSHS-1)讀取氣缸垂直作用在氣浮軸承上的承載力大小；氣膜厚度由微位移傳感器(DGC-8ZG/D，精度0.01 μm)測得；LMS(SCADAS)共12個通道，前端升級動態檢測系統的頻率采集范圍是0～40 MHz，掃描精度±2%；微振動信號由2個單軸PCB加速度傳感器檢測，具體型號分別為：① LW195334， 靈敏度為100.8 mV/g， BIAS級別為11.0 VDC；②LW195333，靈敏度為99.6 mV/g，BIAS 級別為11.1 VDC。

圖3 氣浮微振動測試裝置

2.3 實驗方法和過程

搭建微振動測試平臺如圖3(a)所示，為了驗證微振動的產生原因主要是由三維氣旋波動引起的，將2個單軸方向PCB傳感器安裝在氣浮塊的上表面和周向側面如圖3(c)所示，從而總結出空氣靜壓軸承在不同工作條件及不同方向上的幅頻特性。當空氣靜壓軸承表面載荷分布不均勻時，等效在軸承表面發生偏載作用，導致整個氣膜內湍動氣流不對稱流動。實驗進一步對比分析了發生不同偏載時，空氣靜壓軸承微振動特性的變化規律及分布載荷位置對空氣靜壓軸承微振動的影響。標定實驗后，每組測試數據重復3～5次，偏離平均值較大的數值舍去。圖4所示為分布載荷測試示意圖，在軸承背面標識出不同半徑的分布圓(圖4(a))，根據偏載情況選擇合適的配重砝碼布置于相應的力臂分布圓上，從而等效出載荷分布不均勻時在軸承表面形成的偏載力矩。圖4(b)及圖4(c) 分別為配重砝碼和等效偏載作用效果。

圖4 分布載荷測試示意圖

表1所示為空氣靜壓軸承在不同載荷重量及分布位置的載荷力矩數據表，a、b、c、d4個點如4(a) 所示，每個作用點上分布相應質量砝碼后對空氣靜壓軸承施加的載荷如表中數據所示。例如當a、b兩點同時作用2 kg載荷后，則軸承受到載荷力矩為3 N·m。同理，當軸承上施加多個載荷或者不同方向上作用載荷時，可以根據力矩矢量疊加原理求得作用在軸承上的載荷力矩。發生偏載時，氣膜內局部氣阻和氣容的變化可以消耗更多的湍流動能。因此，有必要著重研究載荷分布在不均勻時氣膜內部渦激振動的敏感因素。

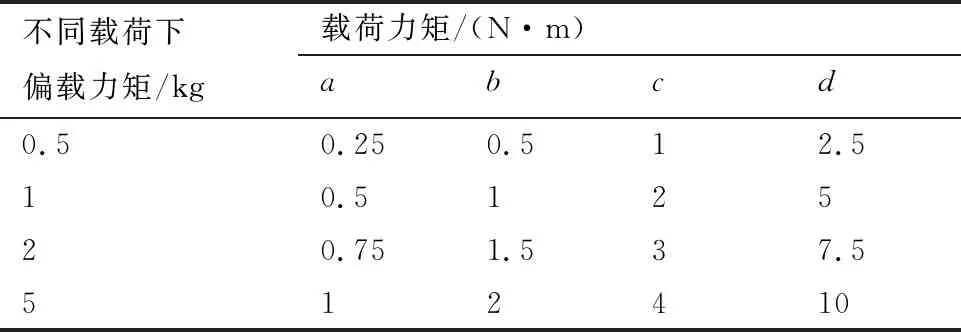
表1 不同條件下的載荷力矩

3 結果分析及討論

3.1 三維微振動驗證

根據數值模擬及實驗觀察分析，氣膜內的渦激振動是由于三維的氣流湍動和壁面之間的耦合作用引起的，所以空氣軸承在工作過程中表現的微振動也是三維方向的。如圖5所示：在豎直方向和平面半徑方向上，ps=0.2 MPa和ps=0.6 MPa下，大供氣壓力下振動幅值明顯比小供氣壓力下的振動幅值大，且相同條件下沿豎直方向的微振動幅值遠大于沿平面半徑方向的微振動幅值。其次，較小的氣膜厚度會帶來更大的振動強度。

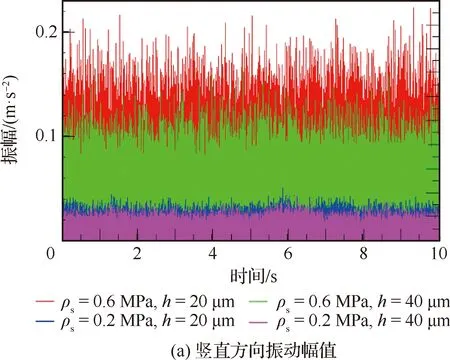
圖5 不同供氣壓力下的時域對比圖

由于氣浮支承的振動受供氣壓力的影響較大，供氣壓力越大氣膜振動越大，而氣膜厚度的改變對微振動的影響主要對沿垂直高度方向上的微振動幅值增強較明顯，而對沿平面半徑方向的微振動影響相對較小，因為氣膜厚度變化在豎直方向上給氣旋(特別是壓力腔內主旋)形成和發展提供了一定的變化空間和發展裕量。另一方面，在不同供氣壓力及不同軸向時，小氣膜厚度(h=20 μm) 的微振動幅值比大氣膜厚度(h=40 μm)的微振動幅值略大。這是因為，當軸承氣膜較大時，氣膜內部的氣旋可以很好地釋放，從而引起支撐氣膜局部振動更小；而當氣膜較小時，氣膜被壓縮區域的局部壓力增加，整個流場內部氣流不穩定，導致微振動幅值增大。

進一步對比圖6中不同氣膜高度下垂直方向微振動強度可以發現：當加入5 kg偏置載荷下，載荷位移分布和供氣壓力不同時，支撐氣膜的剛度和內部氣阻也不相同，此時即使發生相同的偏載，其影響也不同。

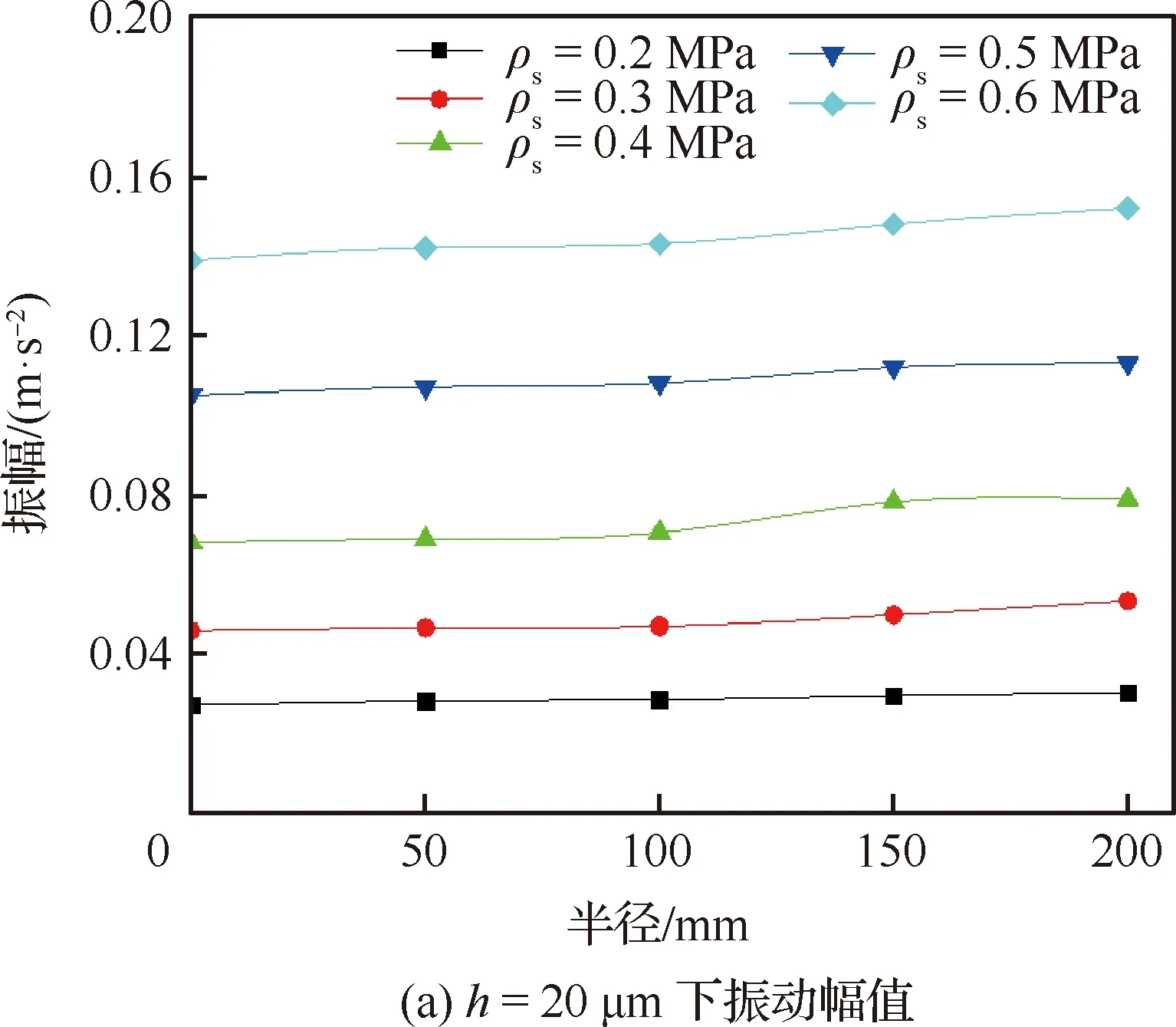
圖6 不同載荷分布下的氣膜振動幅值

隨著供氣壓力的增大，氣膜振動幅值逐漸增大；并且在相同供氣壓力下，大氣膜(h=40 μm)下的振動幅值小于小氣膜(h=20 μm)時的振動幅值。另一方面，在小氣膜(h=20 μm)下載荷分布對氣膜振動幅值不敏感，這時隨著偏載位置的改變，振動幅值略有增大；而在大氣膜(h=40 μm)下，當供氣壓力在中低壓(ps≤0.4 MPa)時，氣膜對偏載影響不大，而當高供氣壓力(ps>0.4 MPa)下，隨著分布載荷偏移位置的增大，振動強度逐漸增強。

由于在供氣孔入口進入氣膜內部流場的過程中存在氣體速度矢量由豎直方向向平面方向轉變，根據動量矩方程可知，空氣軸承必然會受到流場對軸承表面的作用力，伴隨急變流湍動渦旋。進入氣膜以后，在沿半徑方向移動和發展的過程中，氣旋和壁面之間的耦合作用形成了渦激振動。隨著氣膜的逐漸增大，渦激發展越充分，則傳遞給氣浮塊平面的能量越少。如果氣膜越小，則發展受到氣浮塊約束，渦動不能很好地釋放，則此時把自身渦動能傳遞給了氣浮塊，所以振動變大。

如圖7所示：豎直方向和水平方向上的固有頻率和主要倍頻分布大體一致，這主要是由于在同一個氣浮塊的相同方向上，其固有頻率相同，主要的振動頻率范圍也相一致。從整體上對比可以看出豎直方向上的固有頻率及主要倍頻相接近，而水平方向上的固有頻率及倍頻差別較大，這是因為豎直方向氣體的流動自由度被限制住；而水平方向的氣膜流場跟大氣相同，壓力氣體可以自由流動所造成的。

圖7 不同供氣壓力下的氣浮支承振動頻域信號

3.2 分布載荷對微振動強度的影響

不同供氣壓力下氣膜對偏載的敏感性是不同的，由于高壓氣體在發生偏載時，氣膜內各處高度不再統一，導致氣膜內湍動氣流不對稱流動。如圖8所示：當h=20 μm，ps=0.6 MPa，作用5 kg偏置載荷下，當軸承發生偏載時，其振動幅值和正載時相比，偏載作用導致軸承微振動平均幅值由0.44 μm增加到0.53 μm，軸承的微振動強度明顯增大。這是因為：軸承表面發生偏載時引起支撐氣膜局部厚度不均勻，在壓差驅動下，高壓區氣體迅速向低壓區涌動，增大了氣膜內的湍動強度及流場內的渦動能量，導致振動幅值增大。

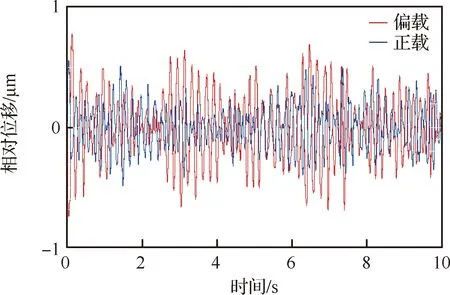
圖8 振動時域特性

進一步分析軸承微振動的頻率特性，如圖9所示：相同供氣壓力下雖然軸承表面載荷分布發生變化，但偏載對微振動的固有頻率和主要倍頻分布影響不大，微振動各階峰值頻率基本穩定在一個相近的范圍內。但是供氣壓力對空氣靜壓軸承微振動的頻域特征影響比較明顯，當供氣壓力較低時，氣浮軸承在氣膜脈動壓力作用下產生的微振動的主要頻率均有所下降。這是由于，供氣壓力較小時氣膜內整體能量水平較低，氣膜流場通過渦激作用對氣浮塊實時做功輸入的能量也較低；隨著供氣壓力增大，壓力能一定程度補充氣腔內部局部壓降造成的黏性阻力損失，同時對氣浮塊做功程度增強，從而提高了軸承微振動的固有頻率和低階峰值頻率。

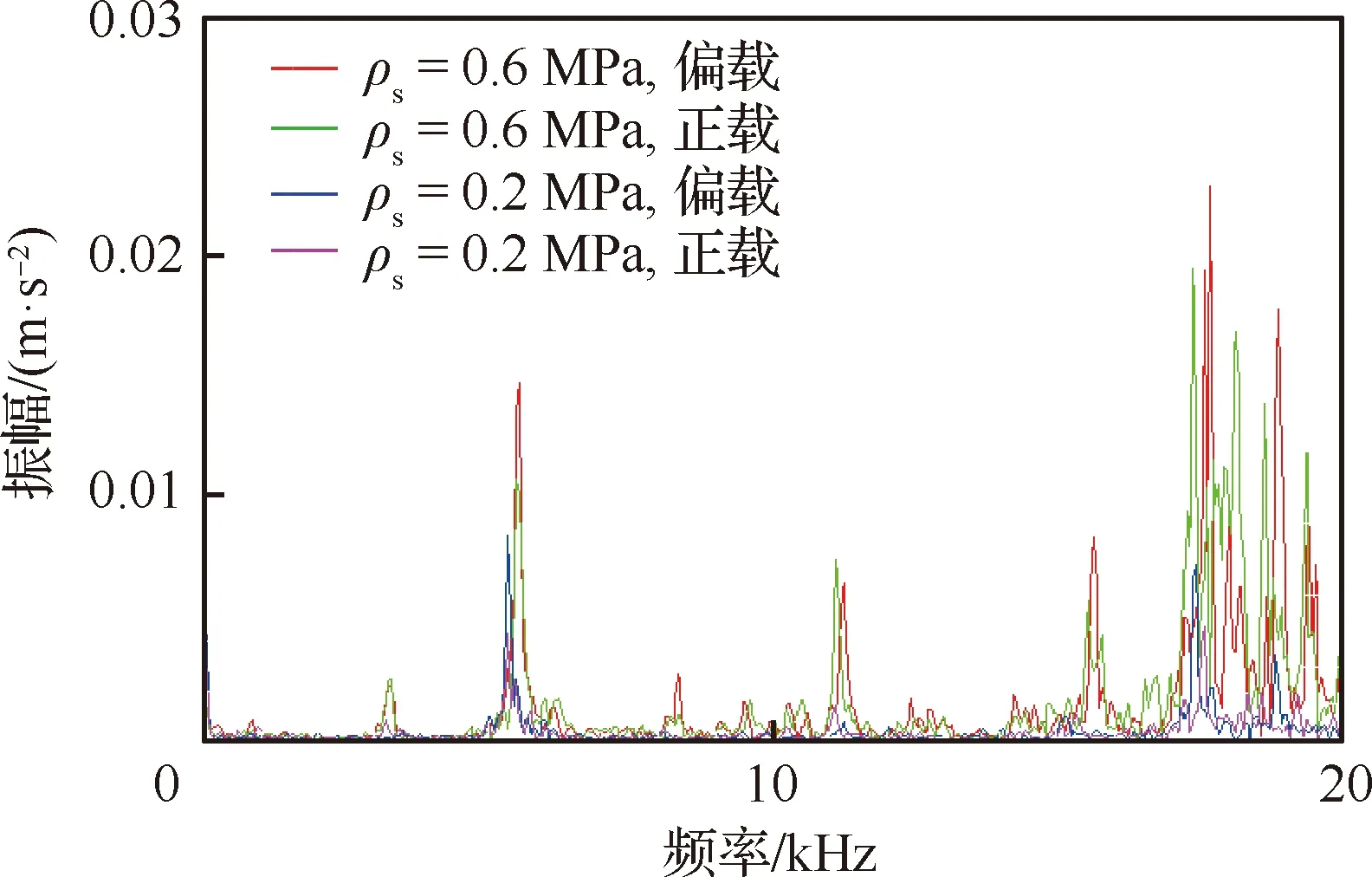
圖9 不同供氣壓力下的的振動頻域特性

由于載荷偏置的出現，使得氣浮軸承表面的受力中心發生改變，不再通過支撐系統的質心，形成偏載力矩，導致此時支撐氣膜的動態阻尼變小，使得振動一定程度地增加。

如圖10所示：當載荷均勻分布時，隨著氣膜厚度的增加，微振動幅值整體降低；當載荷分布不均勻時，隨著氣膜厚度的增加，微振動幅值先降低后增長。其中，當(h≤20 μm) 時，不管是否發生偏載，微振動幅值接近；隨著氣膜厚度增加，當(20 μm

圖10 不同供氣壓力下氣膜振動幅值

特別值得注意的是，當氣膜厚度(h≥35 μm)以后，隨著供氣壓力的增大，由于偏載造成的微振動幅值較載荷均勻分布時差值顯著增大。

綜上，對應不同氣膜厚度下氣腔對稱面上的速度矢量圖，可以按振動情況劃分3個區域，即：① Ⅰ區：渦旋不充分區(h≤20 μm)；② Ⅱ區：渦旋發展區(20 μm

綜上可見：氣膜流場的流動特性和能量傳遞過程，特別是流場內高壓區的湍流渦動及其能量分布，才是決定軸承自激微振動強度和穩定性的最根本依據。不同工況下，載荷的施加及分布形式均會影響靜壓軸承的微振動強度和工作穩定性。所以，在設計和使用空氣靜壓軸承的過程中，對于空氣軸承微振動的分析一定要從流場分析入手，結合具體的結構參數和使用條件，在保證承載和剛度要求的前提下，合理選擇供氣壓力和工作氣膜厚度；在載荷分布不均勻或者發生偏載時，更要使各個參數之間良好匹配，這樣才能保證氣浮支撐系統實現高精度和良好的穩定性。

4 結 論

本文主要通過實驗測試及理論分析相結合的方法分析了載荷分布對氣膜三維微振動特性的影響，比較了氣膜渦激振動在各個方向上的時域和頻域特性。研究發現：不同工況下偏置載荷對軸承微振動的影響不盡相同。

1) 對于空氣靜壓止推軸承，氣膜內的渦激振動是由流場內三維氣旋形成的渦流形成的。而空氣靜壓軸承的微振動成因，核心是氣膜流場流動特性。氣膜高壓區內局部雷諾數較大，湍流程度較高，帶來流場能量的迅速轉化和發展。只有當高壓區渦動能較低，及渦量分布均勻分散時，形成的渦激效應才能有效減小。反之，則會破壞系統的穩定程度。

2) 軸承表面載荷分布不均勻會增加空氣靜壓軸承的微振動強度。對于小孔節流空氣靜壓軸承而言，相同工況下，隨著氣膜厚度的增加，振動幅值逐漸減小。在較大氣膜下，當供氣壓力增加到一定時，隨著分布載荷偏移位置的增加，振動強度逐漸增強；且高供氣壓力對微振動影響更敏感。所以在發生偏載下，為減小軸承的振動強度，提高工作穩定性，必須使用較小的供氣壓力。

3) 軸承氣膜內的渦激振動強度會隨著供氣壓力和氣膜厚度的增加而增加。相同氣供氣壓力下氣體的稠密性降低，導致氣膜振動強度降低，而偏置載荷的加入使得氣浮軸承氣膜流場更為復雜，特別在氣膜厚度較大時，氣膜的氣容量增加，導致偏載對氣浮振動強度影響更加明顯。