基于滑動熵互相關系數與k-means聚類算法的局部特征尺度分解分量篩選方法

盛沛

摘要：提出了一種利用滑動熵以及互相關系數算法對局部特征尺度分解所得分量進行篩選分類的方法。首先對原始信號進行局部特征尺度分解，其次對分解所得的任一分量以及原始信號通過移動起始點的方式計算熵值并計算每一個熵值序列與原始信號的互相關系數，最后利用k-means聚類算法對上述互相關系數進行分類，即可實現分量的篩選。仿真結果表明，該方法能夠有效對局部特征尺度分解所得分量進行篩選，較同類方法具有較大的類間距離。

Abstract： A method of filtering and classifying components obtained from local feature scale decomposition is proposed by using sliding entropy and correlation number algorithm.First local characteristics of original signal scale decomposition， on the second income of any component and the original signal is calculated by means of mobile starting point each entropy is calculated entropy and sequence number of a mutual relationship with the original signal， the use of k - means clustering algorithm to classify the amount of the relationship between each other， the component can be realized in screening.The simulation results show that this method can effectively screen the components obtained from local characteristic scale decomposition and has a larger inter-class distance than similar methods.

關鍵詞：局部特征尺度分解;分量篩選;熵值法

Key words： LCD;component selection;entropy method

中圖分類號：TN911;E917 ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? 文獻標識碼：A ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?文章編號：1006-4311（2020）25-0237-04

0 ?引言

諸如經驗模式分解（Empirical Mode Decomposition，EMD）[1]、局部均值分解（Local Mean Decomposition，LMD）[2]、局部特征尺度分解（Local Characteristic-scale Decomposition，LCD）[3]-[4]等分解方法的優點是具有自適應性，可以在時間尺度上自動將信號按照不同頻帶進行分解。但是，也正是由于其自適應性，導致其分解的結果相對“粗糙”。當信號在幾個特定頻帶能量聚集性較好時，這些算法可將故障特征分離在少數幾個分量中。但實際上這種情況多見于仿真實驗的簡單幾個信號疊加的情況，如文獻[5]等。在大多數情況下，實測的信號故障信息往往在多個內稟尺度分量（Intrinsic scale component，ISC）分量中均有體現，這將對后續處理造成很大不利。在第二種情況下，少數幾個ISC分量不能有效檢測出故障特征或檢驗效果不理想，而取多個ISC分量將會使計算量增大。更進一步講，第幾個ISC分量存在故障信息是未知的，選取過少則信息丟失，選取過多則信息冗余、計算量加大。文獻[6]選取前幾個分量進行故障特征提取及算法比較是基于處理的信號頻段考慮，缺乏理論依據、略顯武斷。

1 ?算法原理及相關概念

在分量篩選方面，相關學者做出了大量研究，目前主要方法一是基于互相關系數，二是基于分量自身信息含量的。前者的理論依據是有用分量必然與原始分量相關性較高，這是從降噪角度出發的一種思考方式，即將分量篩選的過程當成了一種降噪的過程。而后者的理論依據是，諸如峭度、信息熵指標等都是信號非高斯性的一種常用度量指標，大多數情況下信號的高斯特性是數據無序性的一種體現，在工程應用中往往是最“無趣的”，因此，對于故障診斷而言其必然是無用的應該舍去的。文獻[7]將二者結合起來，將分解所得的各分量與原始信號互相關系數較大者以及峭度較大者作為有用分量。這三種方法都具有足夠清晰的物理意義，但從實際應用情況看來，仍存在指標數值區分度不夠大、篩分結果與實際不符等問題。為使有用分量篩選的結果更加準確，本文定義了一種表征信號蘊含故障信息程度的量值——滑動熵-時間序列，將各分量與原始信號滑動熵序列的互相關性作為有用分量篩選指標的方法，具體原理如下：

1.1 互相關系數

互相關系數可以表征兩個信號幅值之間的相互依賴關系，設兩個信號為x（t）、y（t），其互相關系數可表示為：

有用分量與原信號的互相關性系數略小于該分量的自相關系數（分量自相關系數約等于1）;而非有用分量與原信號的互相關系數很小。可通過互相關系數來判定該分量是否為有用分量[8]。

1.2 熵的定義

由信息論可知：在所有隨機變量中，高斯變量熵值最大。進一步講，如果信號是高斯的，則其是最沒有結構特征的。在信號處理領域，那些具有長而尖的概率密度的信號，其熵值應當最小。這往往也是人們最“喜歡”見到的信號，因為它非常有助于進行聚類。熵是信息論中的基本概念之一，離散隨機變量X的熵可以定義為：

1.3 滑動熵的定義

熵值反映的是信號的無序特性，但對細節反映不足，為了從時序細節上觀察信號中無序特征，本文提出一種通過滑動起始點計算各信號段熵值的方法，得到熵值序列。具體計算過程為：

步驟1：對信號x（n）（n=1，2，…，N），確定合適的計算長度l。l的選擇以體現信號中蘊涵的周期成分為原則，通常取l=5～25。

步驟2：分別以x（i）（i=1，2，…，N-l+1）為起點，依次向后截取l個數據點，計算熵值K（i），將K（i）依次排列：

得到滑動熵值-時間序列。

1.4 滑動熵值-時間序列互相關系數

滑動熵值-時間序列即可描述信號非規律特性又具有一定的細節可辨特性。相較于直接互相關系法與熵值法更加貼合分量篩選的目的，即找到對故障狀態分類貢獻最大的ISC分量。

1.5 基于滑動熵互相關系數與k-means聚類算法的分量篩選

經過上述計算過程，對故障診斷有用的和無用的分量已經更容易區分，但仍需要一種方便操作的分量篩選方法。為了避免人為因素干擾，最直接的辦法就是利用聚類算法進行二分類。聚類具體步驟為：

其中：Je為誤差平方和聚類準則，對不同的聚類方案，Je的值不相同，使Je最小的聚類即是最優結果。

綜上所述，本文的分量篩選流程可按以下步驟進行：

步驟1：對故障信號進行LCD，得到若干個ISC分量。

步驟2：計算每個ISC分量與原始信號的滑動熵值-時間序列的互相關系數。

步驟3：以該互相關系數作為聚類指標，采用k-means聚類算法將所有ISC分量進行兩分類——有用分量和無用分量，前者整體互相關系數較大，而后者較小。

2 ?分量篩選方法實例驗證

[算例 1] 考察如下信號：

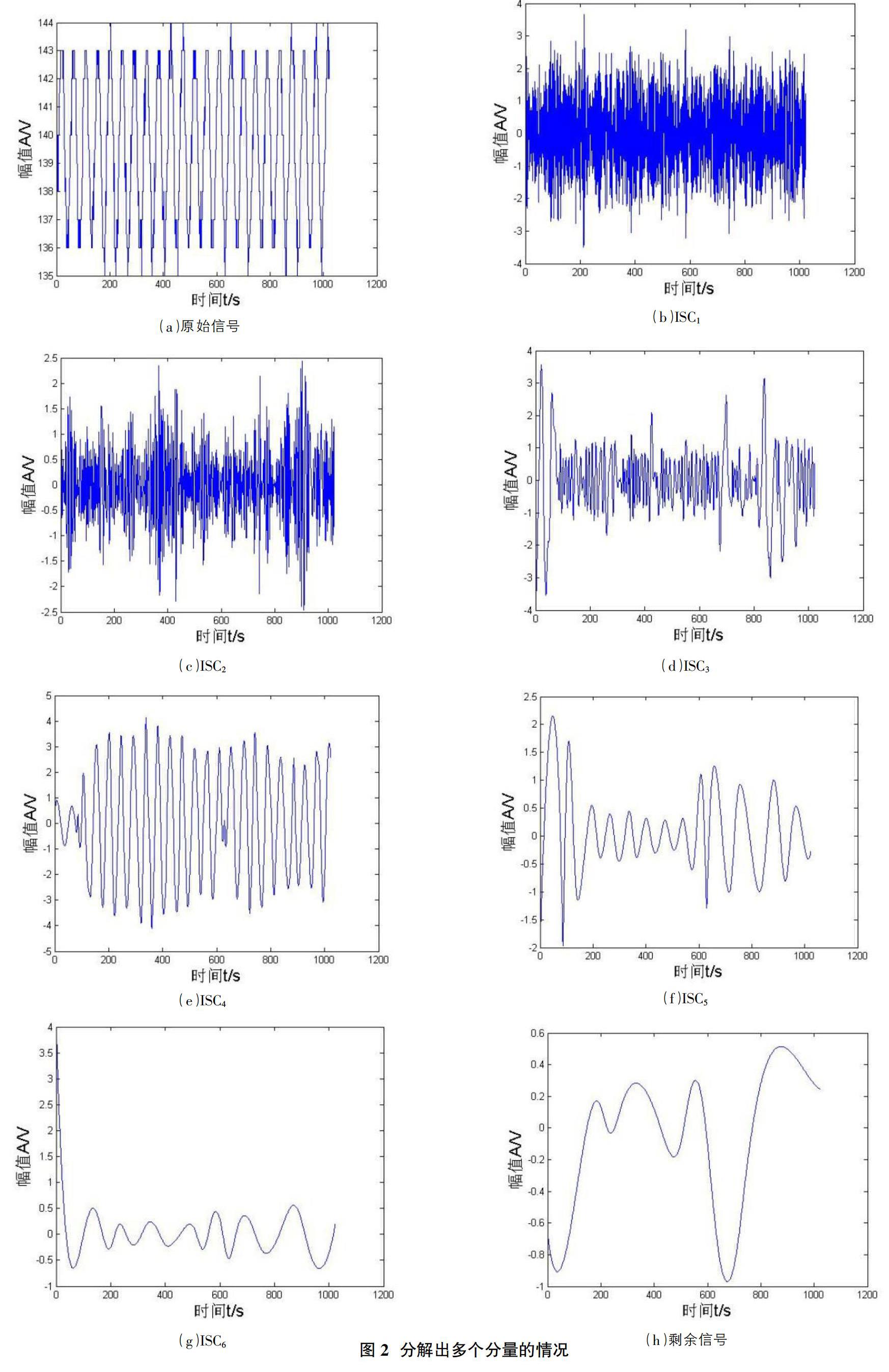
式中：表示信噪比為SNR的高斯白噪聲，SNR按每個采樣點計算，單位dB;f1、f2分別為可變頻率。選取一組信號，不添加噪聲，原始信號如圖 1（a）所示，進行LCD后僅得到圖 1（b）、（c）兩個ISC分量和一個圖 1（d）的剩余信號。可以看出，在信噪比很高的情況下，算例中的合成信號被很好地分解為兩個分量。那么在此種情況下，利用文獻[6]方法將導致后續智能學習機的算法出錯。本文在嘗試利用文獻[6]方法進行后續實驗時，嘗試將缺失分量置零并補齊，但效果仍不甚理想。

在另一方面，對于實測信號而言，大部分實測信號的分解情況則剛好相反——的確會出現文獻[6]所述的超過五個分量的情況。但其有用特征分量的確定卻需做進一步討論。

[算例 2]仍在上例中選取一組信號，但此次添加一微弱高斯白噪聲（SNR=5），對其進行LCD并觀察此次分解結果。混有噪聲的原始信號如圖 2（a）所示，其分解產生的分量及剩余信號如圖 2（b）～圖 2（h）所示。顯然的，第一分量為噪聲分量，文獻[6]取固定前5個分量的做法是錯誤的。

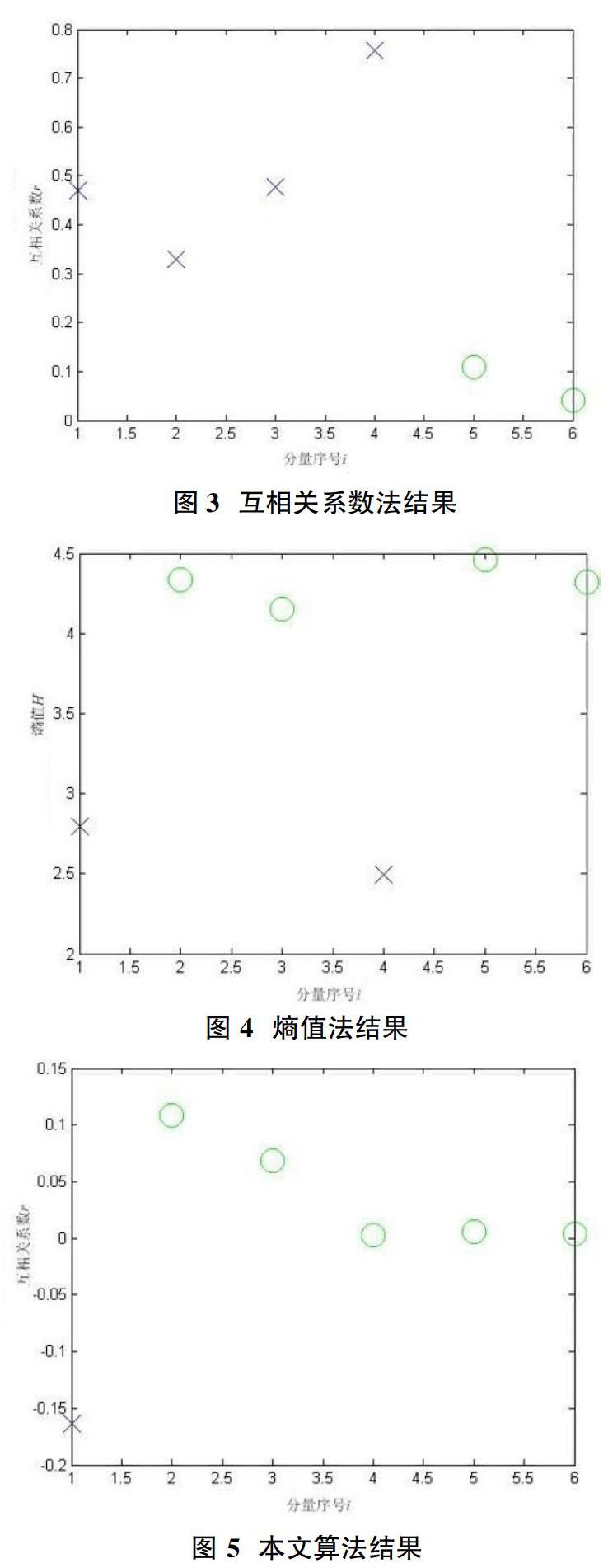
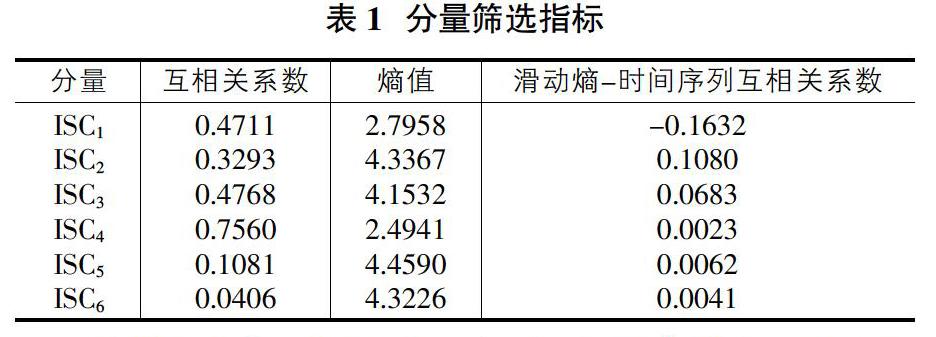
[算例 3] 為了驗證上述分量篩選方法有效性，對上例中得到的各ISC分量分別計算兩種分量篩選指標：各分量與原始信號直接求取所得到的互相關系數、各分量的滑動熵-時間序列互相關系數，并將結果列于表1。

從以上結果可以看出：①互相關系數法排序結果為：ISC4、ISC3、ISC1、ISC2、ISC5、ISC6。按照聚類算法自動聚類，其效果如圖3所示。ISC5、ISC6可視為噪聲或虛假分量，分量篩選結果與前面的分析是一致的，但有用分量與非有用分量間的數值相差不大，不利于區分。②按分量熵值將各分量排序，結果為：ISC5、ISC2、ISC6、ISC3、ISC1、ISC4。按照聚類算法自動聚類，其效果如圖4所示。ISC5、ISC2、ISC6、ISC3的熵值較大，是無用分量，結論與事實不符。因此，依據熵值選取有用分量是存在問題的。③本文算法排序結果為：ISC2、ISC3、ISC5、ISC6、ISC4、ISC1。按照聚類算法自動聚類，其效果如圖5所示。后五個ISC視為有用分量;ISC1視為非有用分量。這與噪聲分量多幾種在高頻部分的論述是十分吻合的。因此依據滑動熵-時間序列互相關系數選取有用分量是準確的。進一步對滑動熵-時間序列互相關系數與直接互相關系數算法在數值方面進行比較分析可知：在有用分量與非有用分量之間，本文算法類間距離相對值更大，區分更加明顯。

3 ?結束語

本文算法是在結合了熵值法及互相關系數算法在局部特征尺度分解有用分量篩選應用方向的成果基礎上產生的，仿真實例證實了其有效性。雖然本文算法數值整體偏小，直觀上看，本文算法相關性數值較小，但是本文追蹤的是信號的非規律性，更能體現故障的本質。本文認為，在故障診斷領域，相對大小相較于絕對大小更有利于達到自動分類的效果。

參考文獻：

[1]Huang N E， Shen Z， Long S R， et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J]. Proceedings of the Royal Society of London. Series A： Mathematical， Physical and Engineering Sciences， 1998， 454（1971）： 903-995.

[2]Smith J S. The local mean decomposition and its application to EEG perception data[J]. Journal of the Royal Society Interface， 2005， 2（5）： 443-454.

[3]程軍圣，鄭近德，楊宇.一種新的非平穩信號分析方法——局部特征尺度分解法[J].振動工程學報，2012，25（2）：215-220.

[4]程軍圣，張亢，楊宇，于德介.局部均值分解與經驗模式分解的對比研究[J].振動與沖擊，2009，28（05）：13-16，201.

[5]鄭近德，程軍圣，聶永紅，羅頌榮.完備總體平均局部特征尺度分解及其在轉子故障診斷中的應用[J].振動工程學報，2014，27（04）：637-646.

[6]張清華，王磊，孫國璽，雷高偉，邵龍秋.基于經驗模態分解的無量綱指標故障診斷定位[J].上海應用技術學院學報（自然科學版），2016，16（01）：17-21.

[7]崔偉成，許愛強，李偉，孟凡磊.基于滑動峭度相關性準則的局部特征尺度分解分量篩選方法[J].計算機測量與控制，2016，24（10）：233-235，239.

[8]張學工.模式識別[M].北京：清華大學出版社，2016.