借助幾何直觀　架構思維橋梁

屈婷　袁凌云

幾何直觀是借助“幾何”手段描述問題、分析問題，從而得出結果。借助幾何直觀，可以將抽象的問題形象化，使隱性的思維可視化。如何提高學生的幾何直觀能力？

一、夯實畫圖技能，培養幾何表征能力

幾何直觀作為一種手段，不能直接作為工具被使用。在教學中，教師要教給學生一些畫圖技巧，培養學生利用圖的直觀表征問題中的數量關系和數學結構的能力。在學生明確兩位數乘兩位數的算理之后，筆者進行了如下教學：

師：筆算14×12時，先算什么？再算什么？

生1：先算14×2=28，再算14×10=140，最后把兩部分積加起來得到168。

師：在學習兩位數乘兩位數時，我們借助點子圖明確了先算什么、再算什么。如果用一個長方形表示14×12的積，如下圖，你能把它分割成兩部分，并說說哪部分表示14×2，哪部分表示14×10嗎？

筆者展示學生的畫法，并根據學生的解釋標上相應數據。

師：上面3種分法都對嗎？

生2：第2種分法不對，14和10不能一樣長。

師：如下圖，如果老師給第一幅圖添一條線段再分割一下，你能看出這4部分分別表示幾乘幾嗎？

生3（指著圖形）：10×10，10×2，10×4，2×4。

師：在筆算14×12時，我們實際上乘了4次。哪部分的面積最大？哪部分面積最小？為什么？

生4：A部分是兩個整十數相乘，面積最大，D部分是兩個一位數相乘，面積最小。

師：試著用這樣的長方形面積圖表示14×12的每一步計算過程，想一想，畫的時候有什么要注意的？

生5：長邊表示大一點的數，短邊表示小一點的數。如果有相等的數，邊的長短要畫一樣長。

生6：不一定要畫那么精確，能表示意思就可以了。

教學中，筆者先出示形象的點子圖，然后過渡到抽象的矩形圖，再到能表征兩位數乘兩位數每一步算理的結構圖，降低了學生用圖形表征的難度。在分割長方形面積的過程中，學生經歷了抽象算式的“圖形化”，提升了將數的運算關系與圖形結構匹配的能力。

二、架構思維橋梁，提升圖形分析能力

幾何直觀的最大優勢是“直觀”， 即跳開計算，能直接“看”出結果。教師要善于打通形象思維與抽象思維之間的通道，提升學生憑借幾何直觀對研究對象進行思考的能力。當學生會使用面積模型表征兩位數乘兩位數后，筆者再引導學生依托圖形探究乘法計算中的規律。

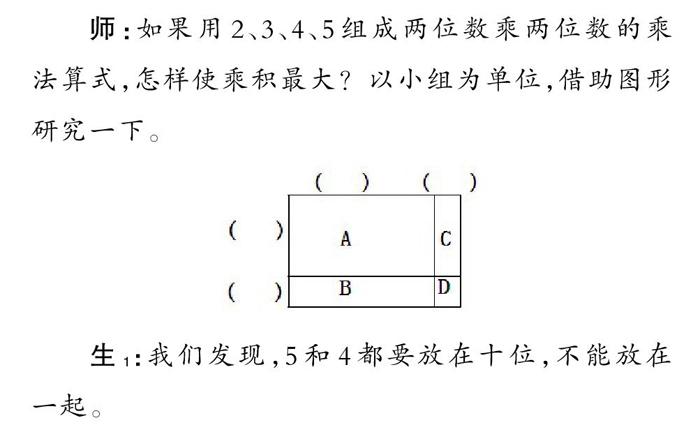
師：如果用2、3、4、5組成兩位數乘兩位數的乘法算式，怎樣使乘積最大？以小組為單位，借助圖形研究一下。

生1：我們發現，5和4都要放在十位，不能放在一起。

師：為什么？5和4都放在十位，相乘得出的是哪個圖形的面積？長方形的面積由哪幾個因素決定？

生2：十位數字相乘得到的是A部分的面積，要使乘積最大，就需要將最大的數字分開放。

生3：要使A面積足夠大，不能只看長，或者只看寬，長和寬要一起看。

師：這個大長方形由4個小長方形組成，為什么你們要把5和4分別放在十位？把5放在個位也能保證C部分的面積最大啊？

生4：A部分的長和寬不管放哪個數字，它的面積都是最大的，要優先考慮。

生5：整十數乘整十數肯定比整十數乘一位數大。既然這樣，肯定要用大一點的數字做A部分的長和寬，這樣才能保證兩位數乘兩位數的乘積盡量大。

師：以前遇到這類問題時，我們做了大量的計算，都沒能說清為什么要將5和4分開放。借助圖形，好像一下子就解釋清楚了。看來，圖形的威力還是挺大的。

生6：我們也確定了十位的數字，個位數字不知道怎么放能保證乘積最大。

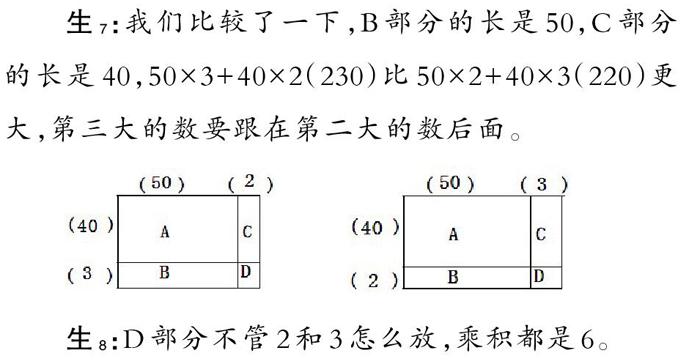
生7：我們比較了一下，B部分的長是50，C部分的長是40，50×3+40×2（230）比50×2+40×3（220）更大，第三大的數要跟在第二大的數后面。

生8：D部分不管2和3怎么放，乘積都是6。

師：看來，A部分和D部分大家沒有爭議，B和C部分需要比較才能得出結論，原來最大數跟最小數、次大數跟次小數相乘的積最大才是最大的。

借助直觀的矩形圖，發現如何寫出乘積最大的兩位數乘兩位數算式，屬于以幾何圖形為載體的幾何直觀，綜合性強，對學生的領悟能力要求更高。4個數字如何放置的規律，巧妙融入5個矩形之間的面積關系之中，既需要兩位數乘兩位數的算理來支撐，又需聯系長方形的面積進行思考。筆者啟迪學生把“數與形”結合起來觀察、思考，透過現象看到本質。長方形面積大小由長、寬的長度決定，積的大小由兩個乘數的大小決定，大長方形的面積取決于4個小長方形的面積和，最大數字和較大數字放在十位，就能保證最大塊的面積最大，這樣就將圖形與算式的內在結構統一起來了，讓學生借助圖形提升了分析能力。

三、啟發想象創造，發展直觀洞察能力

在教學中，教師要啟發學生對圖形進行想象與再創造，將隱藏在圖形背后的關系精細化，發展學生的直觀洞察能力。對于B部分和C部分的面積誰應該優先考慮，能不能借助直觀圖看出來，筆者引導學生有意識地在矩形圖上進行創造。

師：兩位數的十位分別放哪些數字，我們能夠確定，放個位數字時要試驗兩次，那么問題出在哪里？

生1：B部分和C部分。

師（取下第二幅圖B的板貼，與第一幅B部分重合，故作疑惑）：這兩部分到底有什么秘密？如果將2和3的位置互換一下，會發生什么變化？

生2（恍然大悟）：如下圖，我發現把3和2換個位置，用50×2，就會少了這一塊（B部分的陰影部分），用40×3，就會多這一塊（C部分的陰影部分），3當然跟50乘更大，就只能跟在40后面了。

師：少的這塊面積是幾乘幾？多的這一塊呢？

生3：少的面積是1×50，多的面積是1×40。

師：對，寬是1的長方形，當然長越大，面積越大。

為什么“52×43”的乘積最大？兩個長方形，已知長分別是50和40，可搭配的寬是3和2，使面積和最大，如何匹配？實際上，這與“A部分的面積由最大數和次大數相乘就能保證乘積最大”有異曲同工之處。50和40分別作為制約B部分與C部分面積的一個因素，50比40更有優勢，更容易與較大數相乘得到更大的面積，由此相加得到的面積和也會更大。

（作者單位：宜城市窯灣小學）

責任編輯? 張敏