解密一次函數圖象分布

崔秀玲 左效平

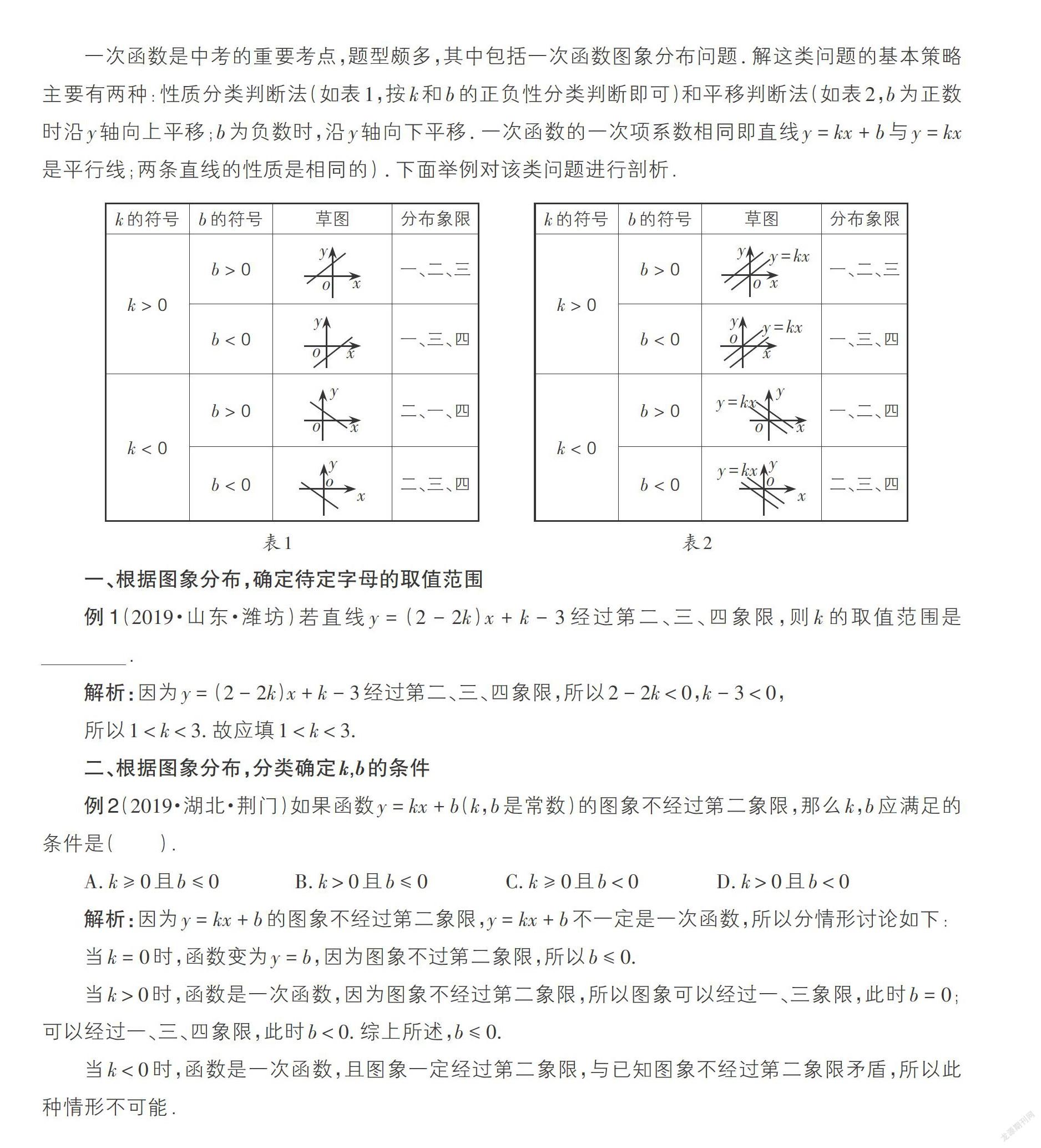
一次函數是中考的重要考點，題型頗多，其中包括一次函數圖象分布問題. 解這類問題的基本策略主要有兩種：性質分類判斷法（如表1，按k和b的正負性分類判斷即可）和平移判斷法（如表2，b為正數時沿y軸向上平移;b為負數時，沿y軸向下平移. 一次函數的一次項系數相同即直線y = kx + b與y = kx是平行線;兩條直線的性質是相同的） . 下面舉例對該類問題進行剖析.

表1? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?表2

一、根據圖象分布，確定待定字母的取值范圍

例1（2019·山東·濰坊）若直線y = （2 - 2k）x + k - 3經過第二、三、四象限，則k的取值范圍是 .

解析：因為y = （2 - 2k）x + k - 3經過第二、三、四象限，所以2 - 2k<0，k - 3<0，

所以1

二、根據圖象分布，分類確定k，b的條件

例2（2019·湖北·荊門）如果函數y = kx + b（k，b是常數）的圖象不經過第二象限，那么k，b應滿足的條件是（ ）.

A. k ≥ 0且b ≤ 0 B. k>0且b ≤ 0 C. k ≥ 0且b<0 D. k>0且b<0

解析：因為y = kx + b的圖象不經過第二象限，y = kx + b不一定是一次函數，所以分情形討論如下：

當k = 0時，函數變為y = b，因為圖象不過第二象限，所以b ≤ 0.

當k>0時，函數是一次函數，因為圖象不經過第二象限，所以圖象可以經過一、三象限，此時b = 0;可以經過一、三、四象限，此時b<0. 綜上所述，b ≤ 0.

當k<0時，函數是一次函數，且圖象一定經過第二象限，與已知圖象不經過第二象限矛盾，所以此種情形不可能.

綜上所述，k ≥ 0且b ≤ 0. 故應選A.

三、根據圖象分布，判斷結論的正誤

例3（2019·貴州·畢節）已知一次函數y = kx + b（k，b為常數，k ≠ 0）的圖象經過一、三、四象限，則下列結論正確的是（ ）.

A. kb>0 B. kb<0 C. k + b>0 D. k + b<0

解析：因為一次函數y = kx + b（k，b為常數，k ≠ 0）的圖象經過一、三、四象限，所以k >0，b<0，所以kb<0. 故應選B.

四、根據k，b的正負性，綜合推理判斷

例4（2019·山東·臨沂）下列關于一次函數y = kx + b（k<0，b>0）的說法，錯誤的是（ ）.

A. 圖象經過第一、二、四象限 B. y隨x的增大而減小

C. 圖象與y軸交于點（0，b） D. 當x>-[bk]時，y>0

解析：因為y = kx + b中k<0，b>0，所以圖象經過第一、二、四象限，所以A正確;因為k<0，所以y隨x的增大而減小，所以B正確;當x = 0時，y = b，所以圖象與y軸的交點為（0，b），所以C正確;當y = 0時，x = -[bk]，根據y隨x的增大而減小，所以當x>-[ bk]時，y<0，所以D不正確. 故應選D.

五、變換待定字母的位置，判斷函數在同一坐標系中的大致圖象

例5（2019·浙江·杭州）已知一次函數[y1] = ax + b和[y2] = bx + a（a ≠ b），函數[y1]和[y2]的圖象可能是（ ）.

[O] [y][y1][y2][1][x] [y][y1][y2][1][x] [y][y1][y2][1][x] [y][y1][y2][1][x] [A][B][C][D][O][O]

解析：在選項A中，由直線[y1] = ax + b可知a>0，b>0，所以直線[y2] = bx + a經過一、二、三象限，所以A正確;在選項B中，由直線[y1] = ax + b可知a<0，b>0，所以直線[y2] = bx + a經過一、四、三象限，所以B錯誤;在選項C中，由直線[y1] = ax + b可知a<0，b>0，所以直線[y2] = bx + a經過一、四、三象限，所以C錯誤;在選項D中，由[y1] = ax + b可知a>0，b<0，所以直線[y2] = bx + a經過一、二、四象限，所以D錯誤. 故應選A.

六、根據圖象平移，綜合求解

例6（2019·湖南·邵陽）一次函數[y1=k1x+b1]的圖象[l1]如下圖所示，將直線[l1]向下平移若干個單位長度后得直線[l2]，[l2]的函數表達式為[y2=k2x+b2]. 下列說法中錯誤的是（ ）.

A. [k1] = [k2]? ? B. [b1]<[b2]

C. [b1]>[b2] D. 當x = 5時，[y1]>[y2]

解析：根據平移性質“直線平行，k值相等”，得[k1] = [k2];根據圖象分布“位于y軸正半軸的b值較大”，可得[b1]>[b2];根據“橫坐標相同時，直線x = a與直線的交點位置靠上的，其函數值較大”，可知當x = 5時，[y1]>[y2] . 故應選B.