三叉星示意圖在高中數學中的應用
李清財
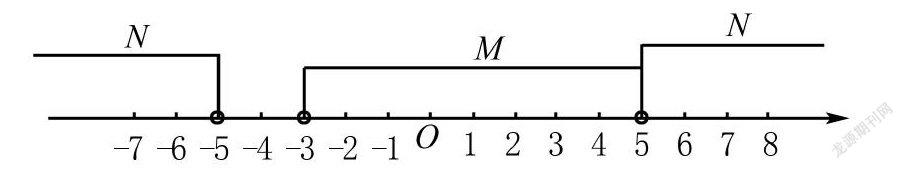

摘 要:三叉星示意圖直觀展示化歸與轉化的條件和方向,以及轉化過程用到的數學方法.三叉星示意圖能夠訓練學生分析條件,找到解決問題的方法,幫助學生全面了解知識內容,提高學生歸納總結能力,從而培養學生數學抽象和數學建模等核心素養.
關鍵詞:三叉星示意圖;化歸與轉化;數學建模
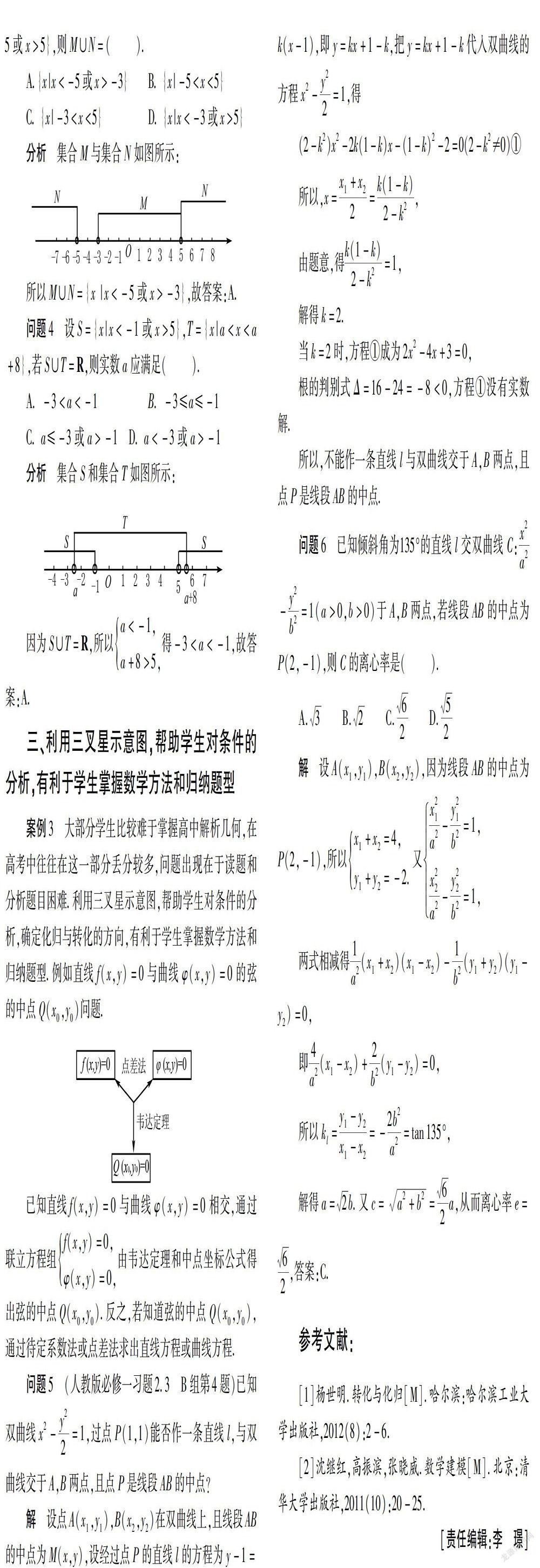
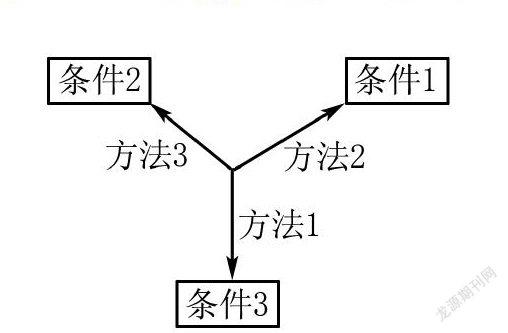
筆者要介紹三叉星示意圖如圖所示:當中有三個對象,只要滿足其中兩個條件,就可以得到第三個結論,即知二求一.利用三叉星示意圖可以把抽象推理過程化為直觀,有助于學生對概念和定義的理解;有助于學生在解決實際問題中進行條件的分析,進一步確定轉化方向;有助于學生歸納總結題型.以下是利用三叉星示意圖的教學案例.
一、利用三叉星示意圖,加深對概念和定義的理解,知道化歸與轉化的方向
案例1 一般地,設函數f(x)的定義域為I,區間DI:如果x1,x2∈D,當x1<x2時,都有f(x1)<f(x2),那么就稱函數f(x)在區間D上單調遞增.
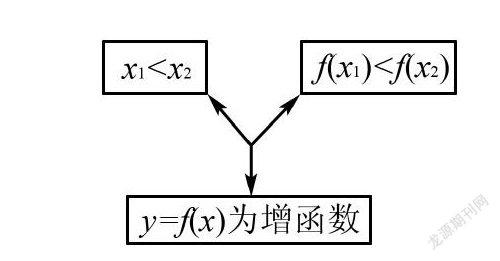
概念的前提與結論利用三叉星示意圖呈現,如下圖:
由滿足其中的兩個條件,就可以得到第三個對應的結論,體現函數單調性的用法,加深對概念的理解.例如:
二、利用三叉星示意圖,幫助學生對條件的分析,有利于數學方法的總結
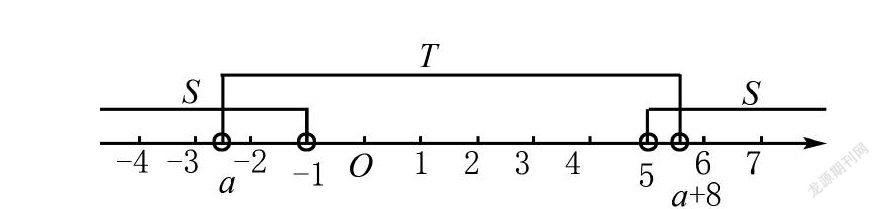
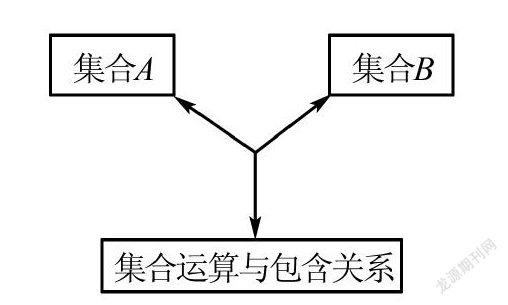
案例2 在高中數學必修一第一單元集合中,涉及兩個集合的基本運算和包含關系,利用三叉星示意圖可以展示解決問題的方法.
而上面三者,知二求一,都可以利用數軸法進行處理.
三、利用三叉星示意圖,幫助學生對條件的分析,有利于學生掌握數學方法和歸納題型
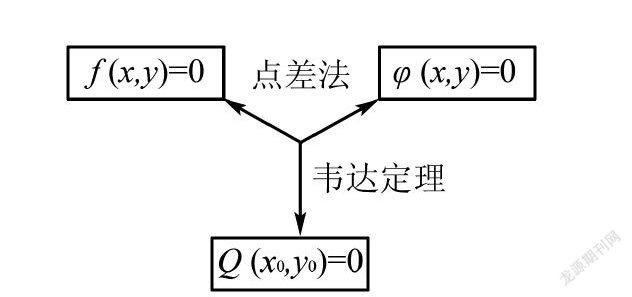
案例3 大部分學生比較難于掌握高中解析幾何,在高考中往往在這一部分丟分較多,問題出現在于讀題和分析題目困難.利用三叉星示意圖,幫助學生對條件的分析,確定化歸與轉化的方向,有利于學生掌握數學方法和歸納題型.例如直線f(x,y)=0與曲線φ(x,y)=0的弦的中點Q(x0,y0)問題.
已知雙曲線x2-y22=1,過點P(1,1)能否作一條直線l,與雙曲線交于A,B兩點,且點P是線段AB的中點?
參考文獻:
[1]楊世明.轉化與化歸[M].哈爾濱
:哈爾濱工業大學出版社,2012(8):2-6.
[2]沈繼紅,高振濱,張曉威.數學建模[M].北京:清華大學出版社,2011(10):20-25.
[責任編輯:李 璟]

