微進給機構垂向剛度建模求解
王夢





摘要:基于一種微進給機構,采用剛柔耦合的方法對機構進行等效建模,在等效模型的基礎上對機構進行受力分析,并應用軟件仿真及數值擬合的方法對機構的垂向剛度進行理論計算,構建起機構的垂向剛度與各項尺寸系數之間的理論模型。為給定垂向剛度下微進給機構的尺寸優化奠定理論基礎。
關鍵詞:微進給機構;等效模型;垂向剛度;受力分析;軟件仿真
0? 引言
微進給機構作為微機械加工及精密加工的執行機構,廣泛應用于精度要求高的非圓對稱截面及非軸對稱截面的加工。因此對機構的性能要求很高[1]。由劉強教授等設計的微進給機構的工作原理是,一個音圈電機和壓電致動器作為驅動元件,兩個彎曲鉸鏈作為導向的機制[2]。但是這種設計易產生垂向跳動。楊志軍教授等設計的一種微進給機構也采用柔性鉸鏈來進行微位移放大,但同時采用對稱雙薄膜機構,對垂向跳動進行了有效抑制[3]。
此微進給機構的拓撲優化可通過有限元優化軟件求解,但是對給定垂向剛度下尺寸優化則需要通過建立理論模型求解。傳統的計算方法如變分法[4]等,求解復雜且不便于后續優化。
本文給出了一種較為簡單有效的方法來求解機構的垂向剛度。并采用軟件驗證及解析法對相關理論公式的推導進行參數修正,建立了機構的等效模型及垂向剛度與機構尺寸參數之間的理論模型。
1? 微進給機構的理論受力分析
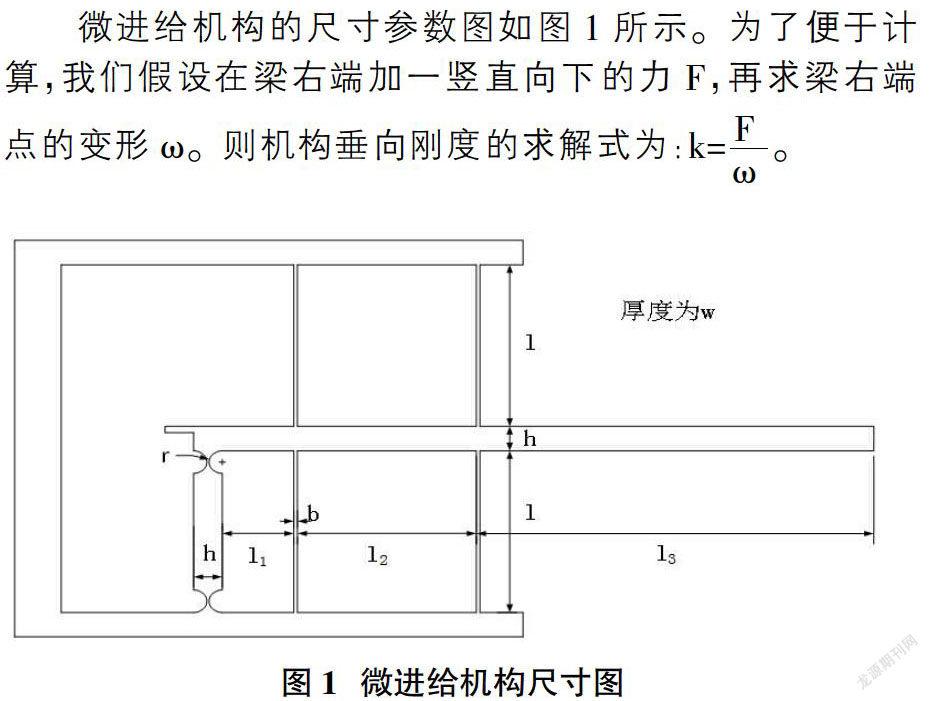
微進給機構的尺寸參數圖如圖1所示。為了便于計算,我們假設在梁右端加一豎直向下的力F,再求梁右端點的變形?棕。則機構垂向剛度的求解式為:
1.1 微進給機構等效模型的建立
在對機構進行受力分析時,參閱相關力學書籍并無直接可以沿用的計算公式。因此本文采用部分剛化疊加的方法來簡化分析,將此機構等效為如下兩個模型:
1.1.1 剛性梁模型
即將薄膜與鉸鏈軸當成柔性的,梁作為剛性。其等效模型如圖2所示。
其中ka為鉸鏈軸的等效拉伸剛度,kb、kc為薄膜的拉伸剛度。
1.1.2 柔性梁模型
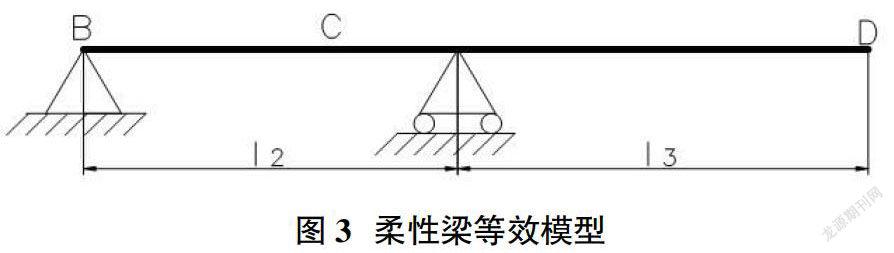
即將薄膜與鉸鏈軸當成剛性,梁當成柔性。其中考慮到柔性梁受梁端點的垂向載荷時,AB段的變形可忽略不計。則其等效模型為:(圖3)
1.2 理論求解
按照上述等效模型,主要包括剛性梁及柔性梁的等效垂向剛度求解。
1.2.1 剛性梁的剛度求解(圖4)
將梁單獨分析:(圖5)
其中,ya、yb、yc分別為鉸鏈軸及薄膜在分力Fa、Fb、Fc下的變形量。有:
其中,ka、kb、kc分別為鉸鏈及薄膜的拉伸剛度。
①薄膜的剛度計算。
按照軸的拉伸剛度計算公式[5],有:
②鉸鏈軸等效剛度的計算。
為了驗證所推導的鉸鏈軸理論拉伸剛度公式的準確性,通過有限元分析軟件Comsol對理論計算公式進行了驗證。驗證結果如表1所示。
可知,不同參數下的理論計算結果與軟件分析結果之間的誤差均在10%以內,是可行的。
1.2.2 柔性梁的剛度求解
柔性梁的模型如圖4所示,其中BC段可等效為兩端鉸接簡支梁,CD簡化為左端點鉸接的懸臂梁。在計算柔性梁的等效剛度時,采用分段剛化來求解。處理的方式為:把梁分段并把每段按受力與變形等效的原則變成表中形式的梁(稱為原梁的等效梁),然后查表按疊加法計算梁的位移[6]。
①CD段剛化。
梁的受力變形示意圖6為:
②BC段剛化。
梁的受力變形示意圖7為:
因為機構可作為剛性模型與柔性模型的串聯,結合式(11)、式(16),知微進給機構的等效垂向剛度為:
2? 軟件驗證
利用多物理場有限元分析軟件Comsol對該機構進行仿真分析。為了得出不同參數下的軟件分析結果,對參數l3進行參數化掃描,將軟件分析結果及理論計算結果進行對比驗證,得到的擬合結果如表2所示。可以看出,理論誤差與分析誤差在10%內。因此用這種方法對于該微進給機構的垂向剛度的理論建模是可行的。
參考文獻:
[1]吳丹,謝曉丹,等.快速刀具伺服機構研究進展[J].中國機械工程,2008,19(11):1379-1385.
[2]Qiang Liu,Xiaoqin Zhou,Pengzi Xu,et al. A flexure-based long-stroke fast tool servo for diamond Turning[J]. International Journal of Aavanced Manufacturing Technology,2012, 59(9-12):859-867.
[3]Zhijun Yang,Weibo Zhou,etc.Modeling and Optimal Design of Membrane Based Fast-Tool-Servo for Freeform Manufacturing of Micro Optical Lens Array[J].Key Engineering Materials.2013,522:411-414.
[4]PAROS J M , WEISBORD L. How to design flexure hinges [M]. Machine Design ,1965:37(27):151-159.
[5]曾祥延.分段剛化法計算變截面梁的變形[J].武漢水利電力大學學報,1994:27(4):405-410.
[6]劉鴻文.材料力學[M].高等教育出版社,2004:188-189.

