基于有限元法的離心泵轉子系統動力學特性研究

張傳東

摘要：本文應用基于有限元法的Workbench軟件對離心泵“干態”和“濕態”條件下的轉子系統進行模態分析，得到兩種條件下的臨界轉速。應用計算流體力學（CFD）中的準靜態法得到了密封口環處的流體激振力并將其添加到“濕態”模態分析中。結果發現，“濕態”條件下，轉子的臨界轉速遠大于“干態”條件下的臨界轉速，這說明密封口環間隙處的流體激振力對轉子起到一定的支撐作用。

關鍵詞：轉子系統;模態分析;“濕態”條件;密封口環;臨界轉速

0 ?引言

轉子系統是旋轉機械的重要組成部分，在離心泵中，轉子系統包括泵軸、葉輪以及聯軸器[1]。在實際工作當轉速接近或達到其固有臨界轉速時，轉子振幅會急劇增加，嚴重影響設備的正常運行，因此準確預測轉子的臨界轉速變得尤為重要。近年來，隨著有限元法的不斷成熟，越來越多的研究人員應用有限元法探究轉子系統的振動規律[2]。付建國等[3]應用基于有限元理論的商務軟件分析了多級離心泵的模態振型。2007年，Q.W. Liang等[4]建立了水輪機的有限元理論模型，將模態分析結果與試驗結果進行了對比，驗證了有限元法的可靠性。隨著研究的進一步深入，相關學者發現密封口環間隙處的洛馬金效應會對轉子系統造成明顯影響[5]，人們把這種考慮了流場激振力的轉子，稱為“濕態”轉子。孫興華等[6]將密封口環處的流體激振力加載到多級離心泵轉子系統中，計算了“濕態”條件下轉子系統的臨界轉速。隨后，姚凌鈞[7]等繼續應用有限元法，將流場中的流體激振力添加到轉子系統的模態分析中，探究了“濕態”條件下泵軸的振動規律。

本文應用基于有限元法的Workbench軟件，對比分析了“干態”和“濕態”兩種條件下葉輪轉子的模態振型和臨界轉速。為計算“濕態”條件下的密封口環處的流體激振力，本文應用CFD準靜態法計算了密封口環的流體激振力。結果發現，密封口環對轉子系統起到一定的支撐作用，“濕態”條件下，轉子的臨界轉速比“干態”條件下轉子的臨界轉速高140%。因此，在設計離心泵時，要考慮密封口環處的流體激振力對轉子系統的影響。

1 ?數值模擬方案

1.1 研究對象

本文研究的對象是單級離心泵葉輪轉子，葉片類型為閉式圓柱葉片，泵的設計揚程H=400m，流量Q=150m3/h，設計轉速為9000rpm，葉片數為6，葉片厚度為5mm，密封口環間隙為0.4mm，密封直徑為202mm，葉輪進口直徑為180mm，葉輪出口寬度為21.5mm，葉輪外徑為284mm，密封長度為30mm。離心泵葉輪轉子部分模型，如圖1所示，轉子部分主要包括葉輪、泵軸以及軸頭螺母。根據材料特點，葉輪材料選用304不銹鋼，泵軸材料為20CrMnTi。

1.2 網格劃分

模型結構較為復雜，應用Swep-Meshing對轉子部分劃分網格劃分四面體非結構網格。網格尺寸設置為5mm，Relevance設置為最大值100，網格數為131317，節點數為221268，網格質量達到要求。

1.3 密封口環動特性參數

密封扣環處的轉子動特性方程[5]，如式（1）所示。本文采用CFD準穩態方法計算密封口環動特性，用FLUENT軟件對密封口環間隙內的液體流動進行數值模擬，密封口環結構示意圖如圖2所示。

在方程式（1）中，K為主剛度，k為交叉剛度，C為主阻尼，c為交叉阻尼，M為附加質量。其中，K、C越大，轉子的臨界轉速越大，k、c越大，轉子的臨界轉速越小;Fτ、Ft為密封轉子在徑向和切向受到的流體激振力。

流體激振力Fτ、Ft，可通過FLUENT模擬結果直接提取，方程組中有6個未知量，至少需要三組Fτ、Ft的值，取渦動比Ω/ω在0.25、0.75和1.25三種工況下的Fτ、Ft帶入方程式（1）中，計算得到密封口環的動特性參數：K=12460571.75N/m，k=1833280.83N/m，C=16941.54N·s/m，c=-19054.46N·s/m，M=13.47kg。最后，將上述值帶入“濕態”轉子模擬中，得到計算結果。

2 ?葉輪模態分析

2.1 “干態”轉子的模態分析

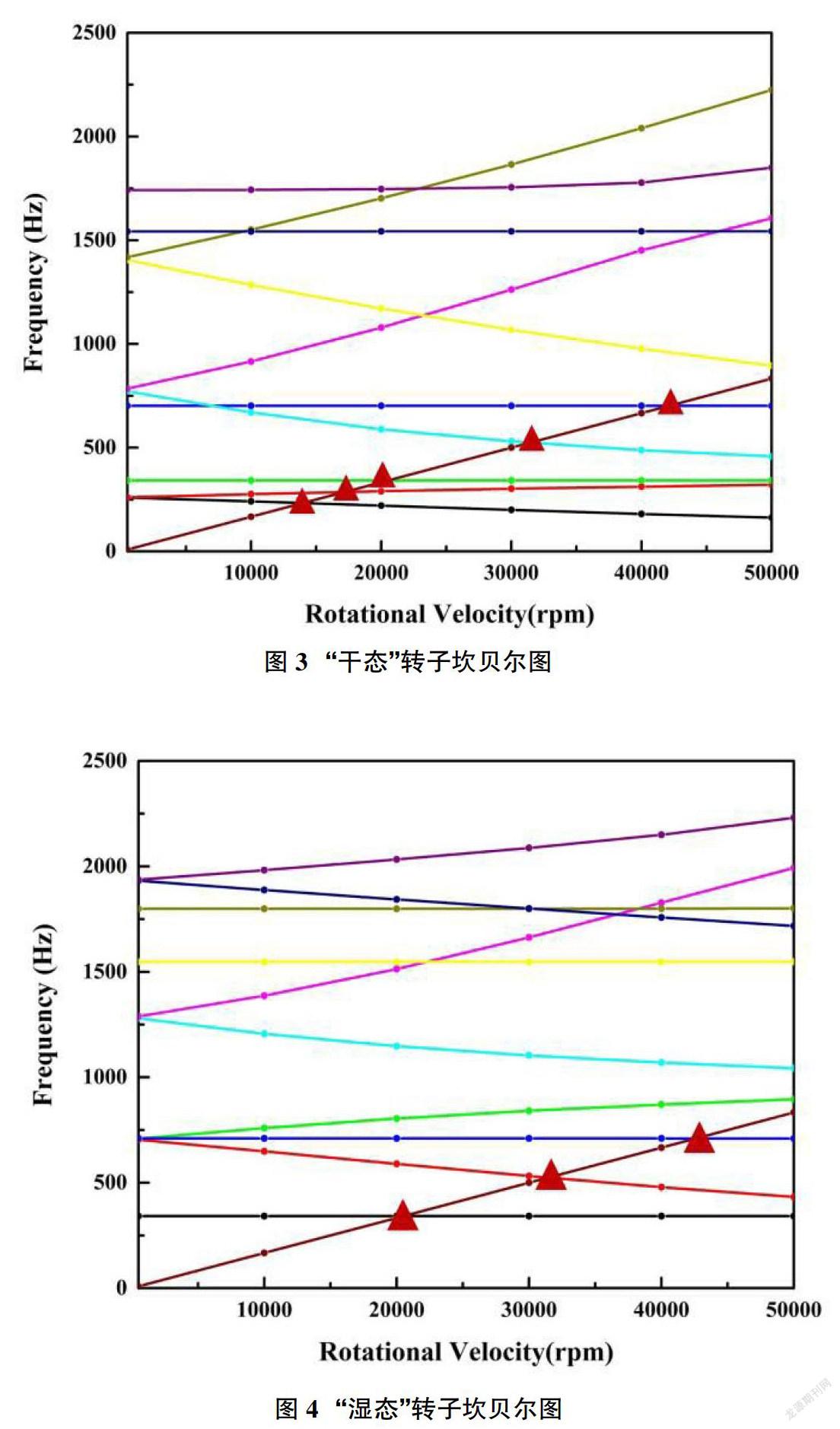
“干態”條件是指轉子在空載狀態下運行下的模態分析，此時密封口環兩端不存在壓差。由于葉輪在泵軸的懸臂端，葉輪轉動產生的慣性力矩不可忽視，故需要考慮陀螺效應對渦動的影響。經數值計算后得到“干態”條件下轉子坎貝爾圖（Campbell Diagram）如圖3所示。

坎貝爾圖是描述轉子臨界轉速的重要方法，根據轉子渦動方向與轉動方向的相同或相反，轉子渦動分為正向渦動和反向渦動，坎貝爾圖中正反渦動頻率與等速度線的交點即轉子的共振頻率點，其對應轉速即為轉子的臨界轉速，在轉子不平衡質量的影響下，轉子渦動方向一般為正向渦動，即渦動方向與轉動方向相同，因此本文只考慮正向渦動下的臨界轉速。從圖3中發現，轉子一階正向渦動的臨界轉速為17055rpm，二階臨界轉速約為一階臨界轉速的2倍，為41271rpm。

2.2 “濕態”轉子的模態分析

“濕態”條件下需要在密封口環處添加彈性支撐，彈性支撐的動特性參數為計算得到的密封口環動特性參數。“濕態”轉子的臨界轉速的坎貝爾圖如圖3所示。

“濕態”轉子的臨界轉速的坎貝爾圖如圖4所示，圖中的正向渦動與反向渦動的頻率與等速度線的交點即轉子的共振頻率，其對應轉速即臨界轉速，“濕態”轉子的臨界轉速有較大提高，正向渦動一階臨界轉速為41744rpm，比“干態”條件下提高了140%。“濕態”下，轉子的密封口環位置的洛馬金效應，等效于滑動軸承的支撐作用，轉速提高，轉子的穩定性增強，所以，為精確計算轉子的臨界轉速，需要考慮密封口環處流體激振力的影響。

3 ?結論

本文應用基于有限元法Workbench軟件，對高速離心泵轉子部分的振動特性進行了研究，結果發現，“濕態”條件下密封口環處的流體激振力對轉子系統的有明顯影響，在一定條件下起到滑動軸承的支撐作用。因此，需要考慮密封口環處的洛馬金效應對轉子系統的影響。

參考文獻：

[1]張新敏，夏延秋，趙清，等.離心泵穩態密封間隙力的計算分析[J].潤滑與密封，2004（04）：63-65.

[2]李啟行，褚福磊.環境激勵下的旋轉機械工作模態參數辨識[J].機械工程學報，2019，55（19）：28-34.

[3]付建國.基于ANSYS Workbench的高揚程多級離心泵轉子模態分析[J].江西水利科技，2016，42（4）：244-248.

[4]Liang Q W， C.G. Rodríguez， Egusquiza E， et al. Numerical simulation of fluid added mass effect on a francis turbine runner[J]. Computers & fluids， 2007， 36（6）：1106-1118.

[5]翟璐璐.離心泵人型槽環流迷宮密封動力學特性數值模擬與試驗研究[D].浙江大學，2015.

[6]孫興華，王躍方，郭婷.離心泵轉子的濕態臨界轉速計算及邊界環境對其動力特性的影響[J].水泵技術，2011（02）：26-30.

[7]姚凌鈞，曹衛東，姜昕，等.基于ANSYS的軸流泵轉子系統有限元分析[J].排灌機械工程學報，2018：1-8.