解題教學中學生高階思維的培養
陳惠增
(福清市高山育才中學,福建 福清 350319)
初中數學解題教學中存在的問題:沒有設計好問題串,對解題只分析求解,沒有進行題后反思;只對題目進行多解羅列,沒有進行優解的歸納;過于定勢思維的解題預設,沒有提出質疑與批判.這樣的解題教學,學生的思維處于“低價”狀態,具體表現為:不可變通性,缺乏深刻性,不成結構性,缺少批判性(即質疑能力).造成上述問題的主要原因:教師解題教學觀念過時、解題教學視野局限、解讀題目膚淺、解題過程功利等.這樣可能阻礙培養學生高階思維能力,從而影響學生數學素養的提升.因此,改變解題教學方式是突破低階思維,培養學生數學高階思維,拓展學生數學思維空間,提高學生的解題能力,提升學生數學解題素養的必然選擇.
一、高階思維及特點
思維是大腦在面對刺激時所進行的一連串活動(Udall&Daniels,1991),Anderson認知目 標分類學(2001)如圖1.

圖1
所謂高階思維,是指發生在較高認知水平層次上的心智活動或認知能力.它在教學目標分類中表現為分析、評價和創造.高階思維是高階能力的核心,主要是指創新能力、問題求解能力、決策力和批判性思維能力.高階思維能力集中體現了數學學科素養的新要求,是適應知識時代發展的關鍵能力,發展高階思維能力是數學課堂教學的應然追求。
高階思維能力是新時代人才發展的必備修養,其表現為思維的層次性、整體性、創新性、批判性等.教師在開展解題教學時,需要結合這些思維特點來進行解題教學,以推動初中學生高階思維能力的形成和發展.從心理學角度來看,智力的核心是思維能力,高階思維能力越強,創新能力也就越強;從社會學角度看,人類的三次科學技術革命,均是由有高階思維能力的人推動的.
二、解題教學中培養學生高階思維的方式
數學教學中注重發展思維是學生能力培養的核心,而培養學生的高階思維能力,對于數學素養的提升和數學關鍵能力的提高,無疑起到了一定的促進作用.基于目前初中數學解題教學存在的問題,如何在解題教學中培養學生的高階思維?本人從初中數學解題教學的實踐出發,提出以下幾點.
(一)設置問題串——培養高階思維的層次性
問題是思維的起點,設置有層次、有梯度的問題,讓學生在思考每個問題的過程中不斷深入,從而通過解決這樣的問題,達到培養學生層次性的高階思維.
例如:已知a+b=5,ab=3,求a2+b2的值.(人教版教材八年級上冊P112.7)
問題1 已知a+b=5,ab=3,求(a-b)2的值.
問題2 已知a+b=5,ab=3,求a-b 的值.
問題3 已知a+b=5,ab=3,求a2-b2的值.
問題4 已知a+b=5,ab=3,求a2+b2的值.
問題5 已知a+b=5,ab=3,求a3+b3的值.
問題6 已知a+b=5,ab=3,求a4+b4的值.
問題7 已知a+b=5,ab=3,求a5+b5的值.
從已知條件出發,有層次地設置問題,所求的結論從簡單到復雜,層層遞進,滿足不同層次的學生的需求,通過這樣問題串設置,培養學生從低階到高階的思維.
(二)通過題后反思——培養高階思維的整體性
“題后反思”,是指解題完成之后,對解題分析過程中所涉及的知識,解題的方法,解題策略或模型的歸納總結.
例如:如圖2,在網格紙中,每個小正方形的邊長為1,A,B,C,D 為格點,線段AB,CD 交于點E,則sin∠AEC 的值為( )
略解分析:解法1(高中公式tan2α=

圖2
如圖3,設格點F,連接AD,BF,
則∠AEC=2∠BAD,
在Rt △ABF中,tan ∠BAD=
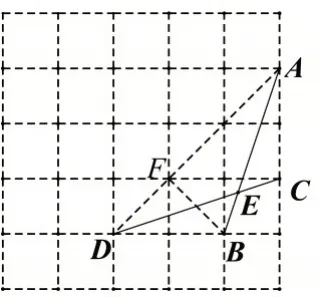
圖3
所以sin∠AEC=.故選C.
解法2:如圖4,連接DF,CF,DH,過點F作FG⊥CD于點G,DF∥AB,則∠AEC=∠FDC,

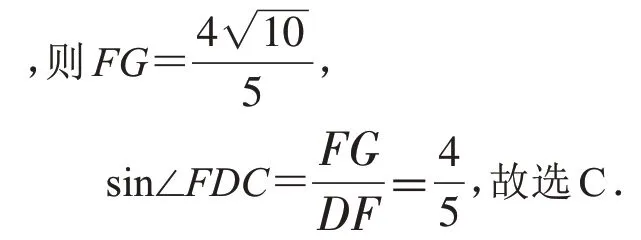
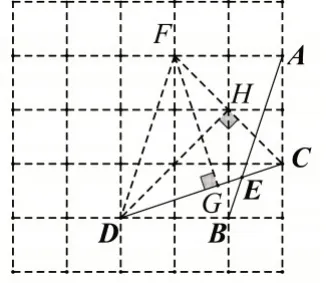
圖4
解法3:如圖5,連接AD,BC,則BC∥AD,

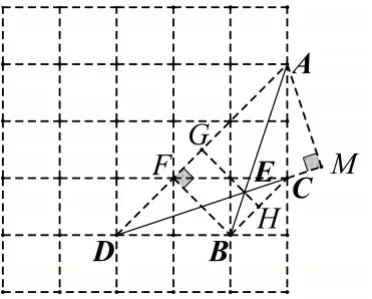
圖5
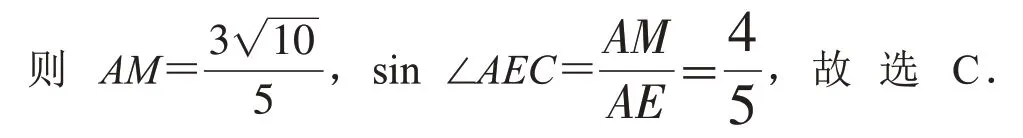
題后反思:1.知識層面:本題所涉及的知識有哪些?從不同的解法中歸納應用到的知識有哪些?
2.方法層面:解法1 是從高中2 倍角公式直接應用而求解,簡單明了,但是超出要求;
解法2,用添加輔助高線,通過等面積法求解;解法3 用相似及等面積法求解.
總之,求解銳角三角函數的值的兩種基本思路:其一是用三角函數的思想求解,即當知道銳角的度數(特別是特殊角度)時,可直接得出其三角函數值;其二是用幾何定義法,即構造直角三角形,通過所對應邊的比而求值.
3.策略(模型)層面
(1)如圖6,倍長矩形MDEC,倍長矩形AFBG中,∠AEC=∠MHC=∠DHE=∠AJG是倍長矩形的模型特征(兩對角線夾角銳角的正弦值).
(2)網格中的問題,從幾何構造角度,應該是多連接一些線,放大圖形(全局角度).
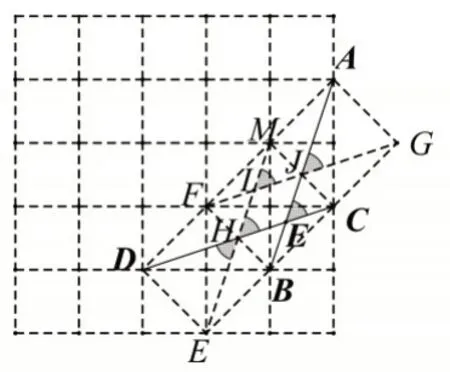
圖6
解題教學中,不但要進行解題分析與求解,更重要的是題后反思,這樣才能培養學生思維的全面性(整體性),使學生從多個角度認識解題及歸納,達到培養學生高階思維的目的.
(三)通過多解選優——培養高階思維的創新性
創新意識與創新能力是培養新時代人才的要求.要創新,就必須先開發思維.數學解題教學中,充分發揮習題潛在的功能,有意識引導學生從不同角度、不同層次去思考與分析,從而培養學生的高階思維的創新性.
例如:如圖7,a∥b∥c,a 與b 之間的距離為3,b 與c 之間的距離為6,a,b,c 分別經過等邊△ABC 的三個頂點,則此三角形的邊長為__________________.
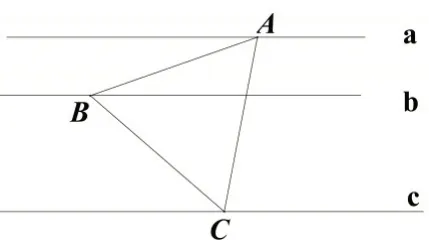
圖7
解法1:如圖8,過點A作AD⊥C于點D,過點B作EF⊥a于F,作EF⊥a于點E,則矩形AFED,BF=3,BE=6,AD=EF=9,DE=AF.
設AB=AC=BC=x.
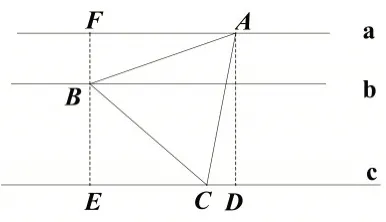
圖8
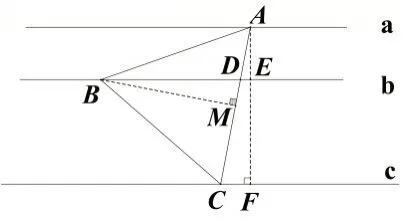
圖9

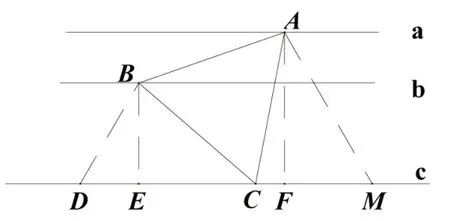
圖10
解題教學過程中,教師要引導學生進行思考,解法1,對于解含三個根號的無理方程,應該通過兩次平方才能達到化去根號的目的,在這種情況下,引導學生上式的等式進行移項變形后:計算會更簡便些.通過對比,發現化成差式相對來說計算量會小些.解法1 列方程相對容易,但解方程很難,超出《義務教育數學課程標準(2011 年版)》的要求,此時,教師可引導學生思考,能否通過其他方式列簡單方程來達到求解的目的?引導學生進行多解思考,達到多解優選的目的,從而可能產生類似解法2 的思路;繼續引導學生再思考,能否不用列方程,就能直接求解呢?可能又如解法3,通過構造“一線三等角”的模型可直接求解.解題過程中,教師不斷引導學生思維升華的思考,這就是高階思維的創新性的體現.
(四)通過打破預設——培養高階思維的批判性
批判性思維是高階思維能力的重要組成部分.建構主義認為“應把錯誤看成學習的一個資源”,學生可以通過“錯誤”引發認識沖突,促進對自己思維過程的批判性思考.
例如,若兩個正方形的邊長比是3:2,其中較大的正方形的面積是18,則較小的正方形的面積是( )
A.4 B.8 C.12 D.16
此題的正確答案是C,而有部分學生選擇了B 的錯誤答案,教師在錯因分析中,總認為學生是因為把兩個正方形的面積比誤認為等于它們的相似比,其實深入了解學生之后,發現有部分同學是因為計算“32=6”錯誤而導致的,即對于這種錯誤的原因分析,可了解真實情況,針對性地配置相應的練習.引導學生對錯因分析的同時,啟發學生發展批判性的思考:“我為什么會錯?怎樣防止下次再錯?”
在解題教學中,還可以打破原有的提示進行批判性的思考.
例如:人教版教材八年級下冊P29 第14 題.
如圖11,△ACB 和△ECD 都是等腰直角三角形,CA=CB,CE=CD,△ACB 的頂點A 在△ECD 的斜邊DE 上.求證:AE2+AD2=2AC2.(提示:連接BD)
證明:如圖12,連結BD,因為△ACB和△ECD是等腰直角三角形,
所 以∠ACB=∠ECD=90°,CA=CB,CE=CD,∠CED=∠CDE=45°.
又因為∠ACB=∠ACD+∠BCD,∠ECD=∠ACD+∠ACE,
所以∠ACE=∠BCD.則△ACE≌△BCD.
所以∠CED=∠CDB=45°,AE=BD.則∠ADB=∠CDE+∠CDB=90°.
在Rt△ADB與Rt△ABC中,
AB2=BD2+AD2=AE2+AD2,AB2=AC2+BC2=2AC2,
即AE2+AD2=2AC2.
課本為了降低題目求解的難度而出現提示,但教師在解題教學中,可提出如若不按提示證明,可否有其他的解法呢?這樣放飛學生的思維,學生就可能想出如下的證明方法:
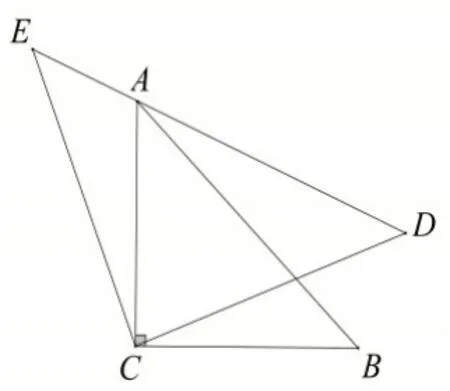
圖11
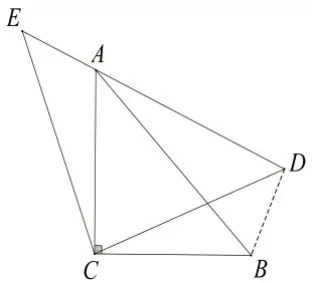
圖12
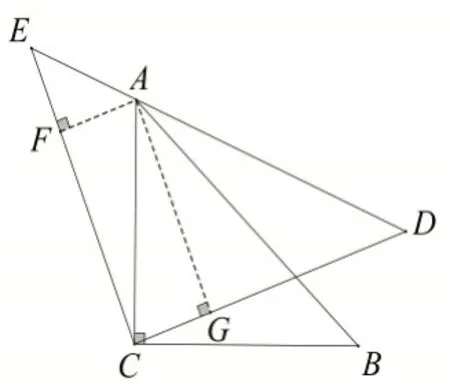
圖13
證明:如圖13,過點A分別作AF⊥CE,AG⊥CD,垂足分別為F,G.
則∠AFE=∠AFC=∠AGC=∠AGD=90°,
因為△ECD是等腰直角三角形,
所以∠ECD=90°,∠CED=∠CDE=45°.
則四邊形AFCG是矩形,即AF=CG.
在△AEF和△ADG中,
由于∠AFE=∠AGD=90°,∠CED=∠CDE=45°,
則∠EAF=∠GAD=45°,即AF=EF,AG=DG.
在Rt△AEF與Rt△AGD中,
AE2=AF2+EF2=2AF2=2CG2,AD2=AG2+DG2=2AG2,
在Rt△ACG中,
由 于AC2=AG2+CG2,則2AC2=2AG2+2CG2=AE2+AD2,
即AE2+AD2=2AC2.
教師繼續啟發引導學生質疑,用類比的思想去思考:在30°的直角三角形或一般的直角三角形中,斜邊上的動點到直角三角形的三個頂點形成的三條線段是否也存在等式關系?從而產生如下的兩個問題:
問題1:如圖14,在△ABC 中,∠ACB=90°,∠A=30°,點P 是斜邊AB 上的一動點.求證:4PC2=PA2+3PB2.
問題2:如圖15,在△ABC 中,∠ACB=90°,點P 是斜邊AB 上的一動點.求證:PC2=sin2A?PA2+sin2B?PB2.
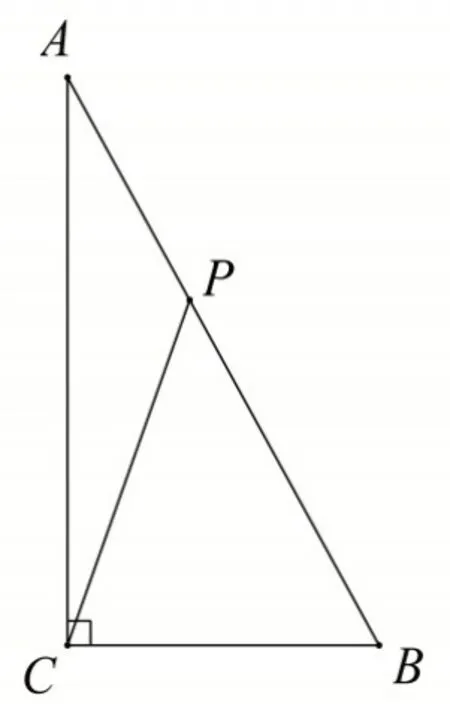
圖14
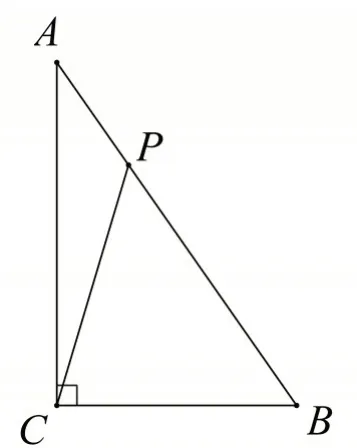
圖15
在解題教學中,教師要善于引導學生質疑,變被動思維為主動思維,通過問題的探究變式,追根溯源,深化其對問題的認識,培養思維的批判性與深刻性.同時加強元認知訓練,指導學生自己思維的過程再認識,形成反思自己思考過程的習慣,達到培養高階思維的目的.

