引導學生利用Matlab 處理大學物理實驗數據的探究
曹躍龍 賈婉麗 張 琳
(西安理工大學理學院 陜西·西安 710048)
0 引言
學生完成物理實驗數據測量后,課后的實驗數據處理是一個重要環節,利用傳統的數據處理方法處理數據,學生往往需要花很長時間完成,傳統的數據處理方法計算繁瑣、容易出錯。如今,運用計算機應用軟件進行實驗數據處理已經成為一種趨勢。Matlab、Mathematica、Maple 等計算機數學語言具有強大的計算功能和繪圖功能,在物理實驗中應用這些軟件進行數值模擬實驗和復雜數據處理非常方便。但是大學物理實驗在本科一年級學生中開設,大部分學生并不具備編程基礎,如何引導學生使用這些軟件完成數據處理就需要我們任課老師潛心研究了。Matlab 相比于高級計算機C 語言而言,簡單易學,上手快,掌握一些簡單的函數完全可以進行實驗數據處理。
1 實驗緒論課講授簡單matlab 函數的必要性
大學物理實驗都是從緒論課開始的,即介紹大學物理實驗的目的、實驗內容、實驗方法,其中一個重要的內容介紹是如何處理實驗數據,常規的實驗數據處理不外乎:列表法、逐差法、作圖法、最小二乘法。這幾種方法都有各自的優點,但也都存在缺點。列表法簡單明了,形式緊湊,各數據間易于參考比較,但也存在不能直觀地顯示數據變化趨勢的缺點。作圖法能將物理量間的對應關系、變化趨勢以及數據的極值點、轉折點、周期性等以最直觀的方式顯示出來,但也存在主觀隨意性大不可避免地引入一些附加誤差。逐差法的優點是計算簡單,可以最大限度的利用測量數據,但要求函數必須滿足一元函數,且自變量必須是等間距變化,函數間不是線性關系的需要轉換成線性關系,這樣的處理都引入了誤差的存在。最小二乘法可以精確地擬合出曲線的參數,但存在計算量過大,學生手工計算難度太大,所以借助于計算機高級語言完成實驗數據處理是很有必要的。
緒論課中可適當引入matlab 的簡單計算函數,鼓勵學生主要通過自學應用matlab 處理實驗數據中的列表法、畫圖法、逐差法以及最小二乘法的繁復計算,使學生學以致用。
2 幾種常用實驗數據處理方法例子
2.1 單變量的統計計算
利用標準偏差表示測量結果時,對于多次測量的樣本標準偏差用 表示

平均標準偏差用
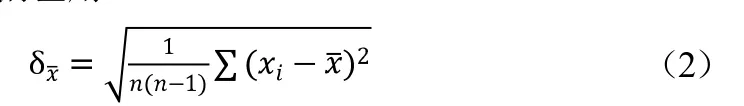
可用的簡單函數有:mean()(求平均值)、var()(求樣本方差)、std()(求樣本標準差)
例如:測量某長度所得數據如下(單位mm):

n(測量次數) 1 2 3 4 5 L(mm) 40.3 39.6 39.7 40.4 39.5 n(測量次數) 6 7 8 9 10 L(mm) 39.8 40.3 39.6 40.5 40.3
試將測量結果按照規范式正確表述。
解:matlab 程序如下:
clear all
L=[40.3 39.6 39.7 40.4 39.5 39.8 40.3 39.6 40.5 40.3];
L1=mean(L) %求解平均值
a1=std(L) %求解樣本標準偏差
a2=a1/sqrt(10) %求解平均標準偏差
運行結果:L1=40.0000mm;
a1=0.3916mm;a2=0.1238mm

2.2 逐差法
用逐差法計算數據,要求原始數據必須是偶數個,必須使用隔n 項逐差,并求對應項的逐差,其算術平均值為:

算術平均值絕對誤差為:

相對誤差為:

例如:一豎直輕彈簧的長度L和下端所加負載質量的關系如下:
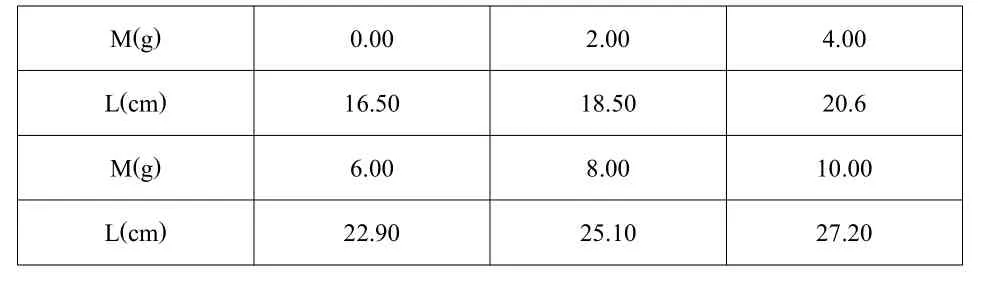
M(g) 0.00 2.00 4.00 L(cm) 16.50 18.50 20.6 M(g) 6.00 8.00 10.00 L(cm) 22.90 25.10 27.20
試用逐差法處理數據,求出伸長量的算術平均值、絕對誤差和相對誤差以及彈簧的倔強系數 。
clear all
g=9.8;
m=[0.00 2.00 4.00 6.00 8.00 10.00];
L=[16.50 18.50 20.6 22.90 25.10 27.20];
delL1=(L(6)-L(3))*10e-2;
delL2=(L(5)-L(2))*10e-2;
delL3=(L(4)-L(1))*10e-2;
delL=1/3*(delL1+delL2+delL3); %算術平均值
delm=(m(6)-m(3))*10e-3;
k=delm*g/(delL) %彈簧的倔強系數
deldelL=1/3*(delL1-delL+delL2-delL+delL3-delL) %算術平均值絕對誤差
E=deldelL/dell %相對誤差
運行結果:彈簧倔強系數k = 0.9000;算術平均值 6.533;算術平均值絕對誤差 2.961 -15%;相對誤差=4.5 -15%。
2.3 一元線性回歸分析

其中a,b 是需估計的兩個參數。現有x 和y 的n 組測量值(,可根據最小二乘法估計 a,b 的值。

所以得到:

R 為線性相關系數。
平均標準偏差為:

其中K 是參數的數目。
例如:一物體作勻速直線運動,在不同時刻t,觀察運動距離S,結果如下:

t(s) 1.00 2.00 3.00 4.00 S(cm) 16.8 22.8 29.0 34.9 t(s) 5.00 6.00 7.00 8.00 S(cm) 40.8 46.6 52.1 58.6
試用最小二乘法求出物體運動速度。
clear all
t=[1.00 2.00 3.00 4.00 5.00 6.00 7.00 8.00];
S=[16.8 22.8 29.0 34.9 40.8 46.6 52.4 58.6];
a=polyfit(t,S,1)%a(1)為 b,a(2)為 a
t1=1:8;k=2;
S1=a(1)*t1+a(2);
Sn=a(1)*t+a(2);tn=(S-a(2))/a(1);
sigmaSn=sqrt((Sn-S)*(Sn-S)'/(k*(k-1))),%S 平均標準偏差

圖1 物體運動距離S 與時間t 的最小二乘法擬合
sigmatn=sqrt((tn-t)*(tn-t)'/(k*(k-1))),%t 的平均標準偏差
tp=mean(t),Sp=mean(S),%平均值
Ltt=(t-tp)*(t-tp)',
Lss=(S-Sp)*(S-Sp)',
Lts=(t-tp)*(S-Sp)',
r=Lts/sqrt(Ltt*Lss),%線性相關系數
運行結果:a=5.9440 10.9893;sigmaSn=0.0025;sigmatn=0.0424;tp=4.5000;Sp=0.3774;r=1.0000
所以速度v=5.944m/s,物體運動的距離S 與時間t 的關系為:s=5.94t+10.99,時間 t 的平均值:t=4.50(s),物體運動距離的平均值:=0.3774(m),時間t 的平均標準偏差為: =0.0424,物理運動距離的平均標準偏差為: =0.0025,線性相關系數為:=1,相關度非常好。
3 小結
通過以上幾種數據處理常用方法的例子可以看出,Matlab功能強大,在物理實驗數據處理中使用非常方便。引入一定的機制鼓勵學生積極自學并使用Matlab 語言來處理大學物理實驗數據,不僅提高了他們自身的素質,而且能夠提高學生學習興趣。

